扩展功能
文章信息
- 周兴业, 王旭东, 苏波
- ZHOU Xing-ye, WANG Xu-dong, SU Bo
- 路面实体结构模型力学响应试验方法研究
- Study on Mechanical Response Test Method for Real Pavement Structure Model
- 公路交通科技, 2017, 34(6): 23-29, 66
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(6): 23-29, 66
- 10.3969/j.issn.1002-0268.2017.06.004
-
文章历史
- 收稿日期: 2016-07-22
2. 交通运输部公路科学研究院, 北京 100088;
3. 中交公路规划设计院有限公司, 北京 100035
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China;
3. CCCC Highway Consultants Co., Ltd., Beijing 100035, China
车辆荷载和环境温度变化会引起路面结构内部产生过大的应力、应变和位移,从而导致路面破坏。多年来,荷载作用下路面的真实力学响应一直是路面结构基础理论与设计的研究重点。目前主要采用理论计算分析和试验实测等方法获取路面结构内部的力学响应规律,这两种方法通常是相辅相成、相互验证的。由于试验实测方法能克服理论分析的某些局限性,较直观地反映路面实际状态,逐渐发展为路面结构力学响应行为研究的重要手段之一[1]。
已有研究中,依托室内外加速加载试验场、足尺环道和实体工程试验路,开展了大量的路面结构力学响应试验实测工作。其中,具有代表性的主要有:澳大利亚ALF加速加载试验[2]、美国HVS和南非MLS直道加载试验[3]、芬兰Virttaa加载试验场[4]等;美国NCAT试验环道[5]、美国内华达州WesTrack[6]、,法国LCPC环道[7]、日本道路工程研究所试验环道[8]、中国交通运输部公路科学研究院足尺环道RiohTrack等;美国AASHTO试验路[9]、明尼苏达州MnRoad试验路[10]、中国山东永久性沥青路面试验路[11]、中国北京六环试验路[12]等。这些试验实测方法采用与实体工程相同或相近的材料类型和结构形式,可较为真实地反映实际路面的荷载情况和环境条件,试验结果与工程实际情况也较为接近,是国内外研究人员公认的一种研究手段[13]。尽管如此,由于大型加速加载试验的复杂程度极高,通常要与之匹配的一整套试验测试和运行管理系统,成本较高,需要有足够的经济基础方能保证其有效运营;此外,受到加载效率的影响,这种试验的周期较长,从试验设计到得出结论,一般需要花费数月到数年的时间。因此,依托大型加速加载试验的路面结构力学响应研究工作,常常受到经济条件和项目研究周期的制约而不能在研究中广泛使用。
鉴于此,为了寻找更具普适性的路面结构力学响应研究方法、获得荷载作用下路面实际力学响应规律,本文设计并制备了一种大比例尺路面结构实体模型,提出了基于该模型的力学响应试验方法,通过室内加载试验对典型路面材料的荷载响应行为进行了分析。
1 试验设计 1.1 路面结构模型尺寸模型与实际路面的尺寸越接近, 越能更好地模拟真实情况,但开展试验加载和结构响应测量越困难。因此,在确定路面结构模型的合理尺寸时,需要找到室内试验与工程模拟之间的平衡点。
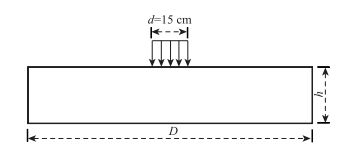
1.1.1 模型形状为便于计算分析,已有研究[14-15]通常将车辆荷载简化为圆形均布荷载,计算体系也可做相应简化。本文借鉴这一处理方法,将路面结构模型形状设计为圆柱体、试验荷载设计为圆形均布荷载[16](荷载圆直径δ=15 cm、施加在模型表面形心处),试验分析体系可相应简化为轴对称空间问题,如图 1所示。
|
| 图 1 路面结构模型设计图 Fig. 1 Design drawing of pavement structure model |
| |
1.1.2 模型厚度
考虑到我国目前高等级公路沥青面层厚度一般为15~22 cm、半刚性基层单层厚度为18~20 cm、水泥路面面板厚度为24~26 cm,为了能更好地模拟实际路面结构,本文将圆柱体路面结构模型的厚度(h)设计为20 cm。
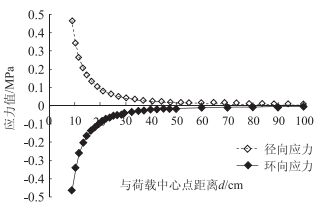
1.1.3 模型直径为平衡室内试验与工程模拟的关系,采用ANSYS有限元软件计算了荷载作用下圆柱体路面结构模型的受力情况。因计算分析体系可简化为轴对称问题,本文取1/4模型的计算结果进行分析(下同)。计算荷载为圆形均布荷载(集度p=2.1 MPa、直径δ=15 cm、施加在模型表面形心处),计算结构模型厚度为20 cm,路面材料选择水泥混凝土(模量E=30 000 MPa、泊松比μ=0.18),计算模型直径(D)取2 m,计算参数为沿直径方向的径向应力应变(σr,εr)和垂直于直径方向的环向应力应变(σθ,εθ),计算结果如图 2、图 3所示。由■2和图 3可知:模型表面径向和环向的应力应变随着与荷载中心点距离(d)的增加迅速减小;当d=30 cm时,径向和环向应力已衰减至0.05 MPa以下;当d=50 cm时,径向和环向应变已衰减至0.5 με以下;d>50 cm之后的应力应变数值太小,对路面结构受力分析而言已经失去意义。因此,考虑到路面结构模型既要较好地模拟实际路面情况, 又要便于开展室内试验研究,本文最终确定模型直径为100 cm。
|
| 图 2 路面结构模型表面应力计算值 Fig. 2 Calculated value of surface stress of pavement structure model |
| |

|
| 图 3 路面结构模型表面应变计算值 Fig. 3 Calculated value of surface strain calculation of pavement structure model |
| |
1.2 试验材料及模型制备
为研究不同路面材料的力学响应规律,本文选取了水泥混凝土、沥青混凝土和水泥稳定碎石等3种典型材料开展路面结构模型荷载响应试验。试验材料的基本信息如表 1所示。
| 水泥混凝土 | 水泥稳定碎石 | 沥青混凝土 | |||
| 强度等级 | C35,fr≥
5 MPa | 级配类型 | CBG20 | 级配类型 | SAC25 |
| 水泥标号 | P.O 42.5 | 水泥标号 | P.O 32.5 | 沥青类型 | AH-70号 |
| 水泥用量 | 389 kg/m3 | 水泥剂量 | 7.5% | 最佳油石比 | 4.3% |
| 试验时抗折 强度 | 6.89 MPa | 试验时抗压 强度 | 5.02 MPa | 15℃抗压强度 | 2.33 MPa |
| 试验时龄期 | 95 d | 试验时龄期 | 38 d | 试验时龄期 | 38 d |
路面结构模型制备时,首先通过大容量拌和设备进行室内拌和,然后人工铺筑于特制模具(直径1 m、厚度20 cm)中,最后采用振动压路机碾压成型。制备好的模型表面较为粗糙,不便于采用电测手段进行应变量测,试验前采用路面打磨机和砂纸对试件表面进行了打磨处理,以保证试件表面的平整,如图 4所示。

|
| 图 4 路面结构模型试件 Fig. 4 Specimens of pavement structures model |
| |
1.3 试验测试系统 1.3.1 加载系统
试验荷载设计为圆形均布荷载,荷载圆直径δ=15 cm,作用位置在路面结构模型表面形心处,通过承载板上配重或液压系统来实现不同荷载水平的静态加载。本文主要使用门式MTS液压伺服系统作为加载装置,利用支撑反力架为路面结构模型提供0~250 kN范围内的任意静态试验荷载,如图 5所示。

|
| 图 5 荷载试验系统 Fig. 5 Loading system for experiment |
| |
1.3.2 力学响应参数量测
本文主要通过在路面结构模型表面粘贴纸基电阻式应变片,如图 6所示,使用“电测法”[17-18]测量荷载作用下模型表面的应变响应情况。应变采集时,利用应变片变形后电阻变化引起的电桥回路中电压变化来记录其工作信息。按此原理,应变片的测试精度经过换算后为0.05 με,静态荷载作用下应变的采集频率为0.1 Hz。

|
| 图 6 电阻式应变片 Fig. 6 Electrical resistance strain gauges |
| |
1.4 试验方案
为研究路面实体结构模型试验方法的可靠性、获得荷载作用下路面结构的实际力学响应规律,本文试验基本方案如下:
(1) 路面结构模型选择水泥混凝土、沥青混凝土和水泥稳定碎石等3种典型路面材料开展试验研究。
(2) 试验荷载为静态圆形均布荷载,荷载圆直径δ=15 cm,通过门式MTS液压伺服系统垂直作用在路面结构模型表面形心处。荷载水平根据3种典型路面材料的破坏强度,按照荷载集度p或应力水平(荷载强度比)两种方式选取。3种路面材料应力水平为0.3时所对应的荷载集度分别为:水泥混凝土p=2.1 MPa,沥青混凝土p=0.7 MPa,水泥稳定碎石p=1.5 MPa。
(3) 考虑到试验分析体系为轴对称空间问题,力学响应参数主要测量结构模型表面沿直径方向的径向应变(εr)和垂直于直径方向的环向应变(εθ)。本文径向应变沿直径方向对称布置成8列,环向应变垂直于直径方向对称布置成2列,研究中取1/4模型对称位置的应变平均值进行试验分析。为了保证每个测试片能够较准确地反映所覆盖位置处的应变信息,应变片之间预留了一定间隔,确保每个应变片工作的独立性,对临近应变比的测量结果不会产生影响。应变片布置情况如图 7所示。

|
| 图 7 应变片布置图 Fig. 7 Layout of strain gauges |
| |
2 试验方法讨论 2.1 试验基本规律
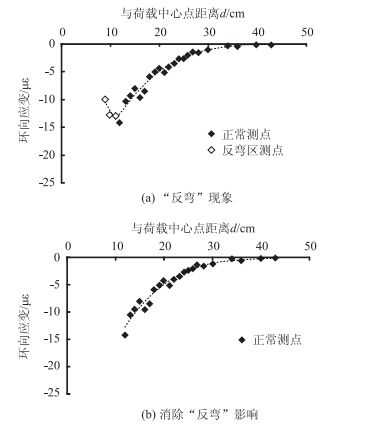
以水泥混凝土路面结构模型为例,对试验的基本现象进行讨论。图 8(a)为静态均布荷载p=2.1 MPa作用下水泥混凝土路面结构模型(1/4模型、下同)表面环向应变的变化规律。由图 8(a)可知,随着与荷载中心点距离(d)的增加,模型表面环向应变数值呈先增大后减小的变化趋势,出现了明显的“反弯”现象,“反弯”峰值点位于距荷载中心12 cm位置处。
|
| 图 8 水泥混凝土模型表面环向应变实测值(p=2.1 MPa,1/4模型) Fig. 8 Measured hoop strain values of cement concrete model (p=2.1 MPa, 1/4 model) |
| |
研究中发现,近荷载端应变实测值的“反弯”现象普遍存在于水泥稳定碎石结构模型和沥青混凝土结构模型试验中,“反弯”峰值点通常出现在距荷载中心点12~15 cm位置处。“反弯”现象的原因可能是,近荷载端的模型表面虽然已经没有荷载的直接作用,但在加载圆边缘(d=7.5 cm)至d=15 cm左右范围内仍然受到荷载边界效应的影响,导致模型表面的受力状态产生了紊乱。因此,为了保证试验结果分析的合理性,研究中将该范围内的测点进行剔除,如图 8(b)所示,以消除荷载边界效应的影响。
2.2 平行性和复现性校验试验方法由于受到测试手段、仪器精度、信号采集方式、环境噪声等因素的综合影响,有时会出现实测值不准确甚至失真的情况。为了保证试验方法的可靠性,研究中对路面结构模型试验方法进行了平行性和复现性校验。本文以沥青混凝土路面结构模型为例,对试验方法的平行性和复现性进行讨论。
表 2和表 3为均布荷载p=0.7 MPa作用下代表性测点处沥青混凝土路面结构模型表面环向、径向应变4次平行试验结果。由表中数据可知,沥青混凝土表面环向应变和径向应变4次平行试验结果的差别很小,变异系数平均值分别为2.1%和2.3%, 属于低变异水平,该试验方法的平行性十分良好。为了保证试验结果的准确性,每次均开展3次以上的平行试验,并取多次试验的平均值作为应变实测值进行对比分析。
| 荷载中心 点距离 d/cm | 环向应变/με | 变异 系数/% | ||||
| 第1次 平行 | 第2次 平行 | 第3次 平行 | 第4次 平行 | 平均值 | ||
| 15 | -28.5 | -29.3 | -28.4 | -28.9 | -28.8 | 1.4 |
| 18 | -25.3 | -26.2 | -24.8 | -25.8 | -25.5 | 0.4 |
| 21 | -19.5 | -18.9 | -20.2 | -19.9 | -19.6 | 2.3 |
| 24 | -14.2 | -14.8 | -13.9 | -14.6 | -14.4 | 2.7 |
| 27 | -10.3 | -10.5 | -9.9 | -10.5 | -10.3 | 2.1 |
| 28 | -8.4 | -8.3 | -8.4 | -8.5 | -8.4 | 3.0 |
| 32 | -7.4 | -7.6 | -7.3 | -7.6 | -7.5 | 1.9 |
| 34 | -5.7 | -5.7 | -5.9 | -5.8 | -5.8 | 2.0 |
| 38 | -4.2 | -4.2 | -4.0 | -4.2 | -4.1 | 2.7 |
| 平均值 | 2.1 | |||||
| 荷载中心 点距离 d/cm | 径向应变/με | 变异 系数/% | ||||
| 第1次 平行 | 第2次 平行 | 第3次 平行 | 第4次 平行 | 平均值 | ||
| 15.3 | -9.7 | -9.4 | -9.7 | -9.8 | -9.6 | 1.8 |
| 19 | -5.4 | -5.6 | -5.2 | -5.5 | -5.5 | 3.2 |
| 21.5 | 2.5 | 2.5 | 2.5 | 2.6 | 2.5 | 1.2 |
| 24 | 5.9 | 5.7 | 6.1 | 6.0 | 5.9 | 3.4 |
| 27.8 | 9.8 | 9.6 | 9.9 | 10.1 | 9.8 | 2.2 |
| 30.3 | 11.3 | 11.8 | 10.8 | 11.7 | 11.4 | 4.0 |
| 34 | 12.8 | 12.9 | 12.6 | 13.3 | 12.9 | 2.3 |
| 36.5 | 7.6 | 7.7 | 7.6 | 7.8 | 7.7 | 0.9 |
| 39 | 6.7 | 6.9 | 6.5 | 6.9 | 6.8 | 3.0 |
| 41.5 | 7.0 | 7.1 | 6.9 | 7.2 | 7.1 | 1.9 |
| 44 | 4.7 | 4.5 | 4.7 | 4.7 | 4.7 | 1.9 |
| 平均值 | 2.3 | |||||
表 4和表 5为均布荷载p=0.7 MPa作用下沥青混凝土路面结构模型表面环向、径向应变3次复现性试验结果,复现性试验的时间分别为:2013年12月7日(第1次),2014年2月21日(第2次),2014年3月1日(第3次),试验温度相同。由表中数据可知,在试验温度相同时,沥青混凝土表面环向应变和径向应变3次复现性试验结果的差别很小,变异系数平均值分别为3.3%和3.8%,小于5%,属于低变异水平,该试验方法具有较好的复现性。由此可见,路面结构模型试验方法具有十分良好的平行性和复现性,试验方法较为可靠,可以作为研究路面结构力学响应行为的一种有效手段。
| 荷载中心 点距离 d/cm | 环向应变/με | 变异 系数/% | |||
| 第1次 复现 | 第2次 复现 | 第3次 复现 | 平均值 | ||
| 15 | -28.5 | -28.9 | -27.9 | -28.4 | 1.7 |
| 18 | -25.3 | -27.3 | -24.8 | -25.8 | 1.8 |
| 21 | -19.5 | -18.2 | -20.0 | -19.2 | 5.1 |
| 24 | -14.2 | -15.2 | -13.5 | -14.3 | 3.1 |
| 27 | -10.3 | -10.4 | -9.7 | -10.1 | 3.0 |
| 28 | -8.4 | -8.0 | -8.5 | -8.3 | 4.8 |
| 32 | -7.4 | -7.8 | -7.1 | -7.4 | 1.1 |
| 34 | -5.7 | -5.4 | -5.7 | -5.6 | 3.6 |
| 38 | -4.2 | -4.4 | -4.1 | -4.2 | 5.8 |
| 平均值 | 3.3 | ||||
| 荷载中心 点距离 d/cm | 径向应变/με | 变异 系数/% | |||
| 第1次 复现 | 第2次 复现 | 第3次 复现 | 平均值 | ||
| 15.3 | -9.7 | -9.5 | -9.8 | -9.6 | 1.8 |
| 19 | -5.4 | -5.8 | -5.4 | -5.5 | 4.2 |
| 21.5 | 2.5 | 2.6 | 2.5 | 2.5 | 2.6 |
| 24 | 5.9 | 5.9 | 6.2 | 6.0 | 3.1 |
| 27.8 | 9.8 | 9.2 | 9.8 | 9.6 | 3.7 |
| 30.3 | 11.3 | 12.1 | 10.6 | 11.3 | 6.4 |
| 34 | 12.8 | 13.7 | 12.5 | 13.0 | 4.6 |
| 36.5 | 7.6 | 7.9 | 7.4 | 7.7 | 3.5 |
| 39 | 6.7 | 6.8 | 6.4 | 6.7 | 3.0 |
| 41.5 | 7.0 | 7.2 | 6.6 | 6.9 | 4.5 |
| 44 | 4.7 | 4.8 | 4.4 | 4.6 | 4.5 |
| 平均值 | 3.8 | ||||
3 典型材料路面结构模型力学响应试验结果分析
研究中选取了水泥混凝土、水泥稳定碎石、沥青混凝土3种典型路面材料制备了结构模型,并开展了相同试验条件(应力水平=0.3, 试验温度为15 ℃)下的力学响应试验。
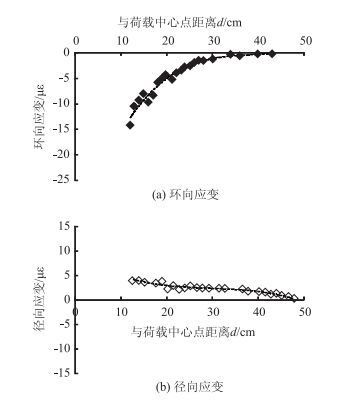
图 9为水泥混凝土结构模型力学响应试验结果。由图 9可知,水泥混凝土表面环向应变为压应变,应变数值随着与荷载距离的增加而减小,至模型边界附近逐渐减小为0;水泥混凝土表面径向应变为拉应变,数值随着与荷载距离的增加而减小,至模型边界附近逐渐减小为0。
|
| 图 9 水泥混凝土模型表面应变实测值 Fig. 9 Measured strain values from surface of cement concrete model |
| |
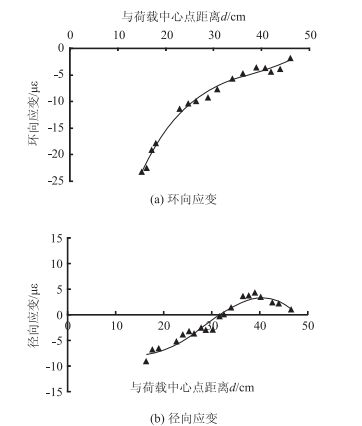
图 10为水泥稳定碎石结构模型力学响应试验结果。由图 10可知,水泥稳定碎石表面环向应变与水泥混凝土的变化规律一致,为压应变,应变数值随着与荷载距离的增加而减小,至模型边界附近逐渐减小为0。水泥稳定碎石表面径向应变呈现压缩-拉伸交替变化,近荷载端的径向应变为压应变最大值,随着与荷载距离的增加,压应变数值逐渐减小为0,之后转变为数值逐渐增大的拉应变,达到峰值点后拉应变逐渐减小,最后至模型边界附近逐渐减小为0。由此可见,荷载作用下水泥稳定碎石表面径向应变具有明显的压应变最大值点、拉压分界点和拉应变峰值点,因它们反映了荷载作用下结构模型的力学响应特征,故称之为力学响应特征点,特征点所对应的数值称为力学响应特征值。水泥稳定碎石材料的拉压分界点出现在距离荷载中心32 cm的位置处,拉应变峰值点出现在距离荷载中心39 cm的位置处。
|
| 图 10 水泥稳定碎石模型表面应变实测值 Fig. 10 Measured strain values from surface of cement stabilized macadam model |
| |
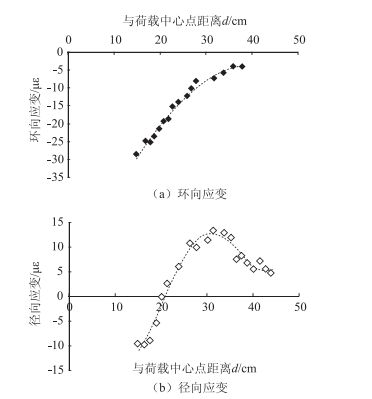
图 11为沥青混凝土结构模型力学响应试验结果。由图 11可知,沥青混凝土表面环向应变与水泥混凝土、水泥稳定碎石的变化规律一致,为压应变,应变数值随着与荷载距离的增加而减小,至模型边界附近逐渐减小为0;受路面材料性质的影响,模量越大, 应变数值越小,即:沥青混凝土的环向应变数值最大, 水泥稳定碎石次之, 水泥混凝土最小。沥青混凝土表面径向应变的变化规律与水泥稳定碎石相似,均呈现压缩-拉伸交替变化,同时也存在力学响应特征点,但几个特征点出现的位置更靠近荷载中心,位置分别为:拉压分界点出现在距离荷载中心点21 cm的位置处, 拉应变峰值点出现在距离荷载中心32 cm的位置处。由这一试验现象可以推断,近车辆荷载的沥青路面结构会处于受压区,而稍远离车辆荷载的位置处则为受拉区,当荷载较重而导致受拉区最大拉应变较大时,可能会引起沥青路面表面开裂,从而形成荷载型Top-Down裂缝。由此可见,在试验条件相同时,不同路面材料的受力情况存在明显差别。
|
| 图 11 沥青混凝土表面应变实测值 Fig. 11 Measured strain values from surface of asphalt concrete |
| |
4 结论
(1) 路面结构模型力学响应试验方法具有良好的平行性和复现性,试验方法较为可靠,当不具备大型加速加载试验条件时,可以作为研究路面结构力学响应行为的一种有效手段。
(2) 通过3种典型材料路面结构模型的力学响应试验发现,在试验条件相同时,不同路面材料的受力情况存在显著差别。水泥稳定碎石和沥青混凝土表面径向应变具有明显的力学响应特征点,即:压应变最大值点、拉压分界点和拉应变峰值点,而水泥混凝土则不存在。
(3) 近车辆荷载的沥青路面结构会处于受压区,而稍远离车辆荷载的位置处则为受拉区,当荷载较重而导致受拉区最大拉应变较大时,可能会引起沥青路面表面开裂,从而形成荷载型Top-Down裂缝。
本文所开展的路面实体结构模型力学响应试验方法可以获得路面材料在结构中的实际工作状态,能够在大量实测数据积累和统计分析的基础上,探讨路面材料在结构中的真实服役状态,从而为路面结构计算和材料参数确定提供参考。
| [1] | 肖川, 邱延峻, 黄兵. 基于车辆加载试验的沥青路面动力响应分析[J]. 公路交通科技, 2014, 31(12): 12-19 XIAO Chuan, QIU Yan-jun, HUANG Bing. Analysis on Dynamic Response of Asphalt Pavement Based on Vehicle Loading Test[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 12-19 |
| [2] | 陈少幸, 张肖宁, 孟书涛, 等. 基于ALF加速加载试验的沥青层疲劳损伤[J]. 公路交通科技, 2012, 29(1): 18-22 CHEN Shao-xing, ZHANG Xiao-ning, MENG Shu-tao, et al. Fatigue Damage in Asphalt Layer Based on ALF Accelerated Loading Test[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1): 18-22 |
| [3] | PEREZ S A, BALAY J M, TAMAGNY P, et al. Accelerated Pavement Testing and Modeling of Reflective Cracking in Pavements[J]. Engineering Failure Analysis, 2007, 14(8): 1526-1537 |
| [4] | 吴明涛, 梁锡三. 各类卡车对道路路面的影响[J]. 广东公路交通, 1998(1): 48-52 WU Ming-tao, LIANG Xi-san. Effect of Different Trucks on Road Pavements[J]. Guangdong Highway Communications, 1998(1): 48-52 |
| [5] | BAKER H B, BUTH M R, VAN DEUSEN D A.Minnesota Road Research Project:Load Response Instrumentation Installation and Testing Procedures, Report No.MN/PR-94/01[R].Maplewood:Minnesota Department of Transportation, 1994:1-34. |
| [6] | TSAI B W, HARVEY J T, MONISMITH C L. Wes Track Fatigue Performance Prediction Using Miner's Law[J]. Transportation Research Record, 2002, 1809: 137-147 |
| [7] | 张鹏, 国兴玉, 王旭光, 等. 足尺路面加速加载试验设备技术研究[J]. 山东交通学院学报, 2011, 19(4): 41-45 ZHANG Peng, GUO Xing-yu, WANG Xu-guang, et al. Research on Experiment Equipment Technology of Full-size Road Surface Loading[J]. Journal of Shandong Jiaotong University, 2011, 19(4): 41-45 |
| [8] | JOHN B M. Application of Full-scale Accelerated Pavement Testing[M]. Washington, D.C.: Nation Academy Press, 1996. |
| [9] | HUANG Y H. Pavement Analysis and Design[M]. Upper Saddle River, NJ: Prentice Hall, 1993. |
| [10] | PRIEST A L, TIMM D H. A Full-scale Pavement Structural Study for Mechanistic-empirical Pavement Design[J]. Journal of the Association of Asphalt Paving Technologists, 2005, 74: 110-114 |
| [11] | 韦金城, 王林, 杨永顺, 等. 永久性沥青路面试验路力学响应分布的数值仿真[J]. 公路交通科技, 2010, 27(6): 15-19 WEI Jin-cheng, WANG Lin, YANG Yong-shun, et al. Numerical Simulation of Mechanical Response of Perpetual Road Test Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 15-19 |
| [12] | 董泽蛟, 柳浩, 谭忆秋, 等. 沥青路面三向应变响应现场实测研究[J]. 华南理工大学学报:自然科学版, 2009, 37(7): 46-51 DONG Ze-jiao, LIU Hao, TAN Yi-qiu, et al. Field Measurement of Three-direction Strain Response of Asphalt Pavement[J]. Journal of South China University of Technology:Natural Science Edition, 2009, 37(7): 46-51 |
| [13] | 田泽峰, 范兴华, 刘云全. 足尺沥青路面加速加载试验实践导论[M]. 沈阳: 东北大学出版社, 2012. TIAN Ze-feng, FAN Xing-hua, LIU Yun-quan. Introduction of Full Scale Accelerated Pavement Test on Asphalt Pavement Practice[M]. Shenyang: Northea-stern University Press, 2012. |
| [14] | 郭大智, 冯德成. 层状弹性体系力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001. GUO Da-zhi, FENG De-cheng. Layered Elastic System Mechanics[M]. Harbin: Harbin Institute of Technology Press, 2001. |
| [15] | 姚祖康. 沥青路面结构设计[M]. 北京: 人民交通出版社, 2011. YAO Zu-kang. Structural Design of Asphalt Pavements[M]. Beijing: China Communications Press, 2011. |
| [16] | JTG D50—2006, 公路沥青路面设计规范[S]. JTG D50—2006, Specifications for Design of Highway Asphalt Pavement[S]. |
| [17] | 徐世烺, 余秀丽, 李庆华. 电测法确定低强混凝土裂缝起裂和等效裂缝长度[J]. 工程力学, 2015, 32(12): 84-89 XU Shi-lang, YU Xiu-li, LI Qing-hua. Determination of Crack Initiation and Equivalent Crack Length of Low Strength Concrete Using Strain Gauges[J]. Engineering Mechanics, 2015, 32(12): 84-89 |
| [18] | 张静, 魏连雨, 马士宾, 等. 动载作用下半刚性基层沥青路面动力响应现场测试及数值模拟[J]. 公路交通科技, 2016, 33(10): 19-24 ZHANG Jing, WEI Lian-yu, MA Shi-bin, et al. Field Test and Numerical Simulation of Dynamic Response of Semi-rigid Base Asphalt Pavement under Moving Vehicle Load[J]. Journal of Highway and Transportation Research and Development, 2016, 33(10): 19-24 |
 2017, Vol. 34
2017, Vol. 34
