扩展功能
文章信息
- 李彦瑾, 罗霞, 车国鹏
- LI Yan-jin, LUO Xia, CHE Guo-peng
- 突发拥挤条件下城市道路网脆弱性识别
- Vulnerability Identification of Urban Road Network under Abrupt Congestion Condition
- 公路交通科技, 2017, 34(5): 129-136
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(5): 129-136
- 10.3969/j.issn.1002-0268.2017.05.018
-
文章历史
- 收稿日期: 2016-07-26
城市路网的突发事件(自然灾害、交通事故,节日游行等)具有成因复杂、涉及面广和高度不确定性等特点。该类事件造成的道路拥挤常使得车辆在路段上排队溢出的可能性更大,交叉口更容易出现连锁拥挤,进而造成大面积路网堵塞。为了应对突发事件导致的路网局部失效,降低突发拥挤对路网整体运输效率的不利影响,分析城市道路的网络拓扑结构,掌握特定环境下的路网脆弱性分析方法意义重大。
目前,国内外学者对交通网络时空特征、路网脆弱性及拥堵条件下的交通配流进行了深入研究。在交通网络拓扑结构分析方面,Jennelius等[1]为了识别道路网络的通过能力瓶颈,引入了路段重要性概念来计算路段与交叉口的可靠性;D’Este等[2]基于连通性和节点度等指标对路网整体效率进行了评价;赵玲等[3]应用图论分析了城市路网在不同攻击方式下的鲁棒性;董洁霜等[4]对降雨条件下道路交通流的变化规律进行了分析。在城市道路网脆弱性研究上,Scott等[5]提出了网络鲁棒性指数(Network Robustness Index,NRI),通过建立无约束用户均衡模型计算了NRI指标;Sullivan等[6]进一步修正了NRI法和网络旅行脆弱性(Network Transportation Robustness,NTR)法,完成了具有不同规模网络的敏感性分析;肖瑶[7]则基于复杂网络理论,构建了城市道路网络的综合脆弱性评价体系;张勇等[8]考虑路段断面通过能力,结合鲁棒性指数评价方法建立了含通过能力约束的交通网络配流模型;在拥堵路网的交通配流方法上,Nguyen等[9]较早地分析了交通流的不对称特性,通过计算机求解了拥挤环境下的路网配流问题;卢顺达[10]基于交通管控条件,设计了拥堵交通网络流分配算法;张雄飞等[11]综合考虑拥挤交通网络的特点, 建立了带转向延误和通行能力限制的交通网络配流模型。
上述研究作出了积极的探索,填补了城市路网拓扑结构与脆弱性分析的空白,但在突发拥挤所造成的网络拓扑结构变化,以及该条件下路段排队溢出对路网交通量影响等方面还考虑得较少,尚有完善空间。因此,本文从城市道路的复杂网络特性和存在排队容量限制的交通网络配流入手,在突发拥挤可能出现的路段或交叉口采用遍历法,逐一利用连通度和网络效率等指标对拓扑形态改变后的路网进行计算评价,筛选、识别出对网络鲁棒性影响较大的路段和交叉口,在此基础上构建含有排队容量约束的网络配流模型,并设计求解算法进行算例验证,通过量化路网对应总阻抗的变化完成突发拥挤条件下的路段脆弱性识别。
1 城市道路网络特性分析城市路网一般由路段与交叉口两大元素构成。在对路网进行拓扑结构分析时,常对这两类元素采用基于图论的方法:原始法或对偶法[12]。考虑到原始法在直观、简明地反映路网拓扑结构上具有优势,且更能便于研究者分析网络效率与区位特性,本文选用原始法构建路网形态,为准确量化路网交通特性打下基础。
1.1 路网突发拥挤的拓扑涵义由于突发事件具有随机性和不可预知性,其造成的道路拥堵需从交叉口和路段两方面来分析。为了便于从中观层面量化突发拥挤对路网交通特性的影响,暂不考虑路段排队溢出等因素,假定一旦出现突发拥挤将立即导致路网交叉口或路段失效,故发生在城市道路的突发拥挤将造成以下两类情况[12-16]:
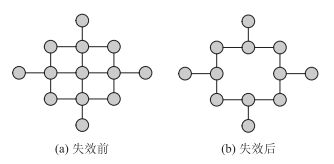
情况1:网络中的节点被除去,其拓扑形态变化如图 1所示。
|
| 图 1 点失效前后路网拓扑形态变化 Fig. 1 Road network topology change before and after point invalid |
| |
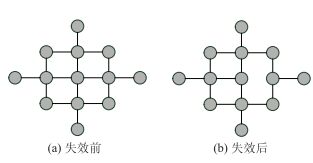
情况2:网络中的边被除去,其拓扑形态变化如图 2所示。
|
| 图 2 边失效前后路网拓扑形态变化 Fig. 2 Road network topology change before and after edge invalid |
| |
图 1与图 2分别从点失效、边失效两个方面刻画了突发拥挤所导致的城市交通网络拓扑形态变化。基于此,本文将路网突发拥挤看作一次随机攻击,则该条件下的路网效率评价可转化为对路网的鲁棒性分析[3]。
1.2 城市路网鲁棒性分析对城市路网而言,鲁棒性分析是指路网中的路段或交叉口在遭受攻击时,路网能保持正常运作的能力,其能力大小由网络效率变化量来定量刻画。变化量越大,说明失效路段或交叉口对路网鲁棒性的影响越显著。本文从中观层面选取反应点的度和介数的鲁棒性评价指标:连通度和网络效率[12]。
(1) 连通度
连通度是网络中实际边数与最大边数的比值。交叉口的突发拥挤造成节点失效,从而影响路网的连通度。连通度在失效前后的变化量越大,表明该节点对路网鲁棒性的影响越显著。网络连通度γ的计算公式为:
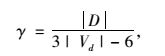
|
(1) |
式中,|D|为网络中边的数目;|Vd|为网络中节点的数目。
当点失效时,统计失效后路网的实际边数|D′|,计算相应的连通度γ′,并按式(2) 计算失效前后路网连通度的变化量Δγ:
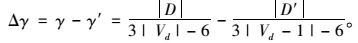
|
(2) |
(2) 网络效率
网络效率是利用边介数效率的均值衡量路网的通行效率。路段突发拥堵导致的边失效,将影响路网的网络效率。网络效率在失效前后的变化率越大,表明该路段对路网鲁棒性的影响越显著。网络效率E的计算公式为:
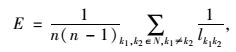
|
(3) |
式中,N为节点集合;n为落网节点总数;lk1k2为连接节点k1,k2间的最短路径。
同理,当边失效时,统计与计算失效后路网的实际边介数lk1k2′与相应的网络效率E′,并按式(4) 计算失效前后网络效率的变化量ΔE:
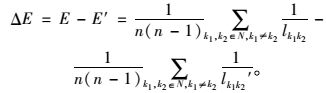
|
(4) |
对于目标城市路网G(N, L),N为路网点集合,L为路网边集合。通过遍历法,逐一去掉路网中的节点i或边lk1k2,分别计算其失效前后的网络效率变化量指标Δγ和ΔE,并通过对变化量进行排序,寻找对鲁棒性影响较大的路网交叉口与路段,按式(5) 得到下阶段进行脆弱性识别的包含潜在关键路段的改进路网G′(N′, L′)。其中N′为对网络鲁棒性影响较大的点集合,L′为对网络鲁棒性影响较大的边集合[17]。

|
(5) |
注意:与原始路网G(N, L)相比,改进路网G′(N′, L′)是通过在模拟突发拥挤条件下,利用路网效率评价指标(点的连通度Δγ、边的网络效率ΔE)的鲁棒性变化值大小,选取出的对路网鲁棒性有显著影响的节点集合N′与边集合L′而构成的。接下来,从原始路网G(N, L)中遍历删除路段a(a∈L′),构建该条件下的路网脆弱性识别模型。
2 拥挤条件下的路网脆弱性识别前面在不考虑流量约束条件下,在中观层面通过鲁棒性分析识别了路网中的潜在关键节点与路段,完成了原始路网的压缩。这既有助于简化模型求解的规模与计算量,又能够有效建立、分析路网鲁棒性与脆弱性的联动关系。
下面考虑各个路段a(a∈L′)的排队容量限制,将突发拥挤前后路网总阻抗的变化作为判别标准,进一步鉴别改进路网G′(N′, L′)的关键路段并完成路段脆弱性识别。
2.1 模型假设在突发拥挤条件下,在一定时间内相应的路段往往会出现车辆超长排队现象。故对此做出如下假设,以便对这一现象进行分析建模:
(1) 假设采用车辆点排队,每辆车的车长均为0。
(2) 假设路网中每条路段的排队容量都是有限的,无法容纳无限多车辆排队。
(3) 假设突发拥挤条件下的路段断面通行能力将迅速下降为0。
(4) 假设同一车道单列行驶,不存在多车并行的情况,则发生拥堵的路段在拥堵结束、路况恢复时,其通过能力将近似等于最大排队容量,即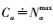
当路网G′(N′, L′)处于完好状态时,设初始路网的总阻抗为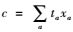
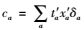
从指标构造过程可以看出,识别指标Δca不仅利用δa考虑了网络空间拓扑特性和路段连通性,而且兼顾了路网中的阻抗变量ta与ta′[8]。
2.3 路段排队容量约束将拥挤路段交通流视为排队系统,则设路段a在发生拥堵时能容纳的最大车辆数即为该路段排队容量Namax,其中单位长度排队车辆数ka与路段排队容量Namax满足:
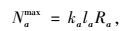
|
(6) |
式中,ka为路段a单位长度的排队车辆数;la为路段a的长度;Ra为路段a的车道数。
路段a的排队容量约束是指在路段阻抗时间ta(xa)内排队停留的车辆不能超过路段a的排队容量,即:
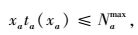
|
(7) |
式中xa为进入路段a的流量。
2.4 模型构建路网脆弱性识别即确定路网在突发拥挤前后道路总阻抗变化相对较大的路段。本文采取的研究方法是:逐一从路网G′(N′, L′)中删除路段a(a∈L′),用于模拟该路段突发拥挤时道路通行能力迅速降为0的假设,再考虑剩余路段的排队容量限制,利用平衡分配法得出路网的交通流量分布,最后依据路段拥挤前后的流量变化,利用路段阻抗计算公式,确定与比较路网总阻抗Δca的大小。
由于网络配流过程是一个复杂、动态的调整过程,在考虑路段容量约束Namax的条件下,路段上流量的变化均会导致其阻抗ca的改变,当达到网络均衡状态时,路段阻抗变化值Δca趋于稳定。故脆弱性识别指标Δca不仅考虑了网络空间拓扑特性和路段连通性,还可视为在路网配流过程中路段重要度的定量刻画。
选用带约束的路网用户均衡模型获得路网上各路段的流量分布,其目标函数为:
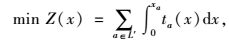
|
(8) |
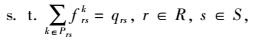
|
(9) |
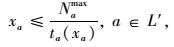
|
(10) |
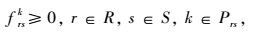
|
(11) |
式中,frsk为起点r与终点s之间的有效路径k的流量;qrs为起点r与终点s之间的交通需求量;xa为路段a的流量;ta(xa)为路段a的阻抗;L′为路网G′(N′, L′)中所有的路段集合;R和S分别为路网中所有出行的起点集合和终点集合;Prs为起点r与终点s之间的有效路径集合。
另外,xa与frsk的关系为:
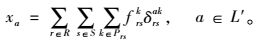
|
(12) |
式中δrsak为0-1变量,表示若起点r与终点s之间的有效路径k经过路段a,则δrsak=1,反之为0。
显然,该模型是凸规划,因此它有唯一的路段流量最优解[11]。
3 求解算法用传统的Frank-Wolfe算法求解上述模型,迭代过程较为繁琐。因此,本文采用Lagrange乘子法,先通过对排队容量约束式(10) 实施惩罚,将原问题转变为一系列无约束规划问题,再用现成的有效方法求解[11]。增广Lagrange乘子算法步骤如下:
Step 1 初始化。选择初始的Lagrange乘子向量u1,路段a对应的初始乘子ua1为:

|
(13) |
式中, ta1为路段a的初始阻抗;xa1为路网中路段a的初始流量,各个路段流量组成初始向量x1。
设置初始罚函数参数ρ1(ρ1>0),迭代数n=1。
Step 2 求解子问题。令路段时间函数为:
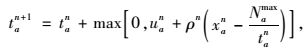
|
(14) |
先利用求路段阻抗最短路的Floyd法[10]求出任意两点间的最短路径,再利用Frank-Wolfe算法解无排队能力约束的交通分配问题,得到路段流量解xn。
Step 3 若收敛判断函数
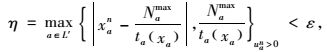
|
(15) |
式中ε为一个很小的正数(取0.05),停止迭代,视{xn, un}为问题最优解,否则转Step 4。
Step 4 更新乘子un+1与罚函数参数ρn+1。新的un+1值按式(27) 计算,新的ρn+1按式(16) 计算:
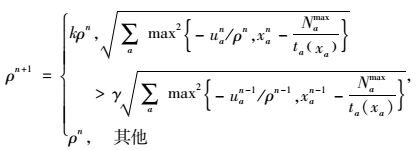
|
(16) |
式中,调整参数k的取值范围是2≤k≤10(取4.5),γ=0.25。令n=n+1,转Step 2。
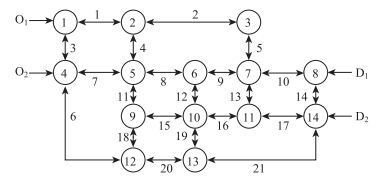
4 算例分析算例网络G(N, L)由2个OD对、14个节点和21条路段组成(如图 3所示)。路段具体参数如表 1所示。网络上的OD对为:(1, 8),(1, 14),(4, 8),(4, 14),共计4对。
| 路段 编号 | 排队容量 Namax/veh | 初始阻抗 ta0/h |
| 1 | 1 000 | 0.1 |
| 2 | 1 000 | 0.1 |
| 3 | 1 000 | 0.1 |
| 4 | 950 | 0.2 |
| 5 | 1 000 | 0.1 |
| 6 | 1 000 | 0.1 |
| 7 | 950 | 0.12 |
| 8 | 1 000 | 0.12 |
| 9 | 1 000 | 0.2 |
| 10 | 1 000 | 0.12 |
| 11 | 1 000 | 0.1 |
| 12 | 950 | 0.2 |
| 13 | 950 | 0.12 |
| 14 | 1 000 | 0.1 |
| 15 | 1 000 | 0.2 |
| 16 | 1 000 | 0.2 |
| 17 | 1 000 | 0.2 |
| 18 | 1 000 | 0.12 |
| 19 | 1 100 | 0.1 |
| 20 | 1 100 | 0.1 |
| 21 | 1 100 | 0.1 |
|
| 图 3 算例网络 Fig. 3 Example network |
| |
表 1与图 3分别表示算例路网的路段基本参数和几何拓扑结构。突发拥挤条件下的城市路网脆弱性识别分两个阶段完成:道路网络特性分析与道路网络脆弱性识别。
(1) 道路网络特性分析
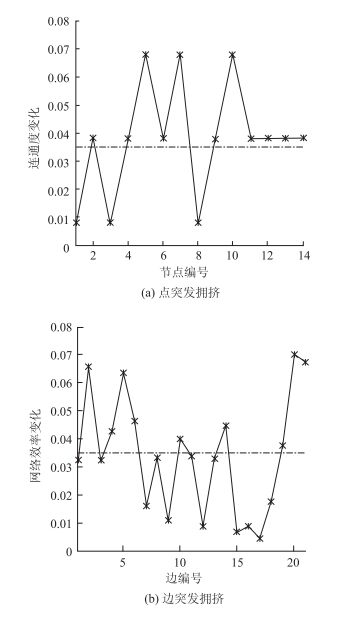
利用连通度与网络效率两个指标完成路网特性指标的分析,分别按式(5)、式(7) 计算该点或边在突发拥挤前后连通度或网络效率指标的变化量。经计算,点或边失效条件下的路网特性指标变化如图 4所示。
|
| 图 4 突发拥挤导致点或边失效后的路网特性指标变化 Fig. 4 Changes of characteristic index of road network after point or edge invalid by burst congestion |
| |
图 4中,连通度变化量Δγ与网络效率变化量ΔE取均值,作为路网G(N, L)节点与边的筛选边界。在突发拥挤造成点失效的条件下,路网连通度变化的均值Δγ=3.5%,选取高于均值的对应节点构成改进后的节点集N′;在边失效的条件下,路网效率变化的均值ΔE=3.41%,同理,选取高于均值的对应边构成改进后的边集L′。集合N′和L′的具体元素如下:
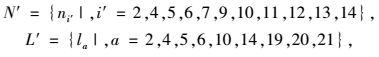
|
(17) |
式中,i′为节点编号,a为路段编号。
路网特性分析指标Δγ与ΔE从中观层面反映道路上各节点或路段在突发拥挤时,其交通功能失效对整个网络鲁棒性的影响。通过筛选出高于指标均值的节点集N′和路段集L′构成新的路网G′(N′, L′),为下阶段考虑路段排队容量的路网脆弱性分析提供基础。
(2) 路网脆弱性识别
设网络上的OD需求为:
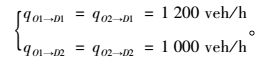
|
(18) |
路段阻抗函数采用BPR函数:
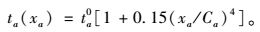
|
(19) |
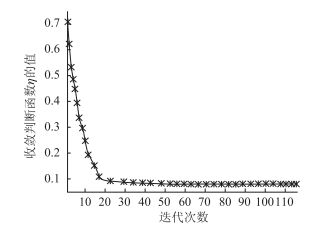
逐一从路网G′(N′, L′)中删除路段a,设置初始罚函数参数ρ1=0.5,收敛判断函数η随着迭代次数增加的变化如图 5所示。
|
| 图 5 收敛函数η值随迭代次数变化 Fig. 5 Convergence function η varying with iteration number |
| |
由图 5可知,随着Lagrange乘子法迭代次数的增加,收敛判断函数η值不断下降,当迭代至18次时,η值趋于平稳,当迭代至116次以后,达到满足收敛条件的均衡数值解。
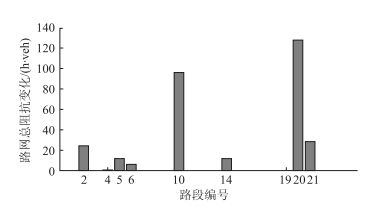
为了分析与识别排队容量约束下的路网脆弱性路段,将路网G′(N′, L′)中各路段在突发拥挤条件下的脆弱性识别指标——路网总阻抗变化Δca值进行对比,如图 6所示。
|
| 图 6 考虑排队容量约束各路段Δca值的变化 Fig. 6 Change of Δca of each road section with queuing capacity constraint |
| |
图 6表明,路网G′(N′, L′)中的各个路段在发生突发拥挤时,对整个路网的总阻抗变化量影响差异显著:路段21、路段20、路段10等路网总阻抗变化较大,而路段4、路段5、路段6、路段14等则变化较小。进一步地,将Δca值按大小排序,并与路网特性指标ΔE值的排序结果进行比较,其结果如表 2所示。
| 排序 | 突发拥挤 | |||
| 路网鲁棒性分析 | 路段脆弱性识别 | |||
| 路段编号 | ΔE/% | 路段编号 | Δca/(h·veh) | |
| 1 | 20 | 6.94 | 20 | 128.310 |
| 2 | 21 | 6.76 | 10 | 96.496 |
| 3 | 2 | 6.63 | 21 | 58.398 |
| 4 | 5 | 6.50 | 2 | 24.427 |
| 5 | 6 | 4.63 | 5 | 11.798 |
| 6 | 14 | 4.55 | 14 | 11.798 |
| 7 | 4 | 4.32 | 6 | 5.965 |
| 8 | 10 | 4.08 | 4 | 0.489 |
| 9 | 19 | 3.85 | 19 | 0.062 |
从表 2可知,在考虑排队容量限制的条件下,通过路段的脆弱性识别,突发拥挤导致的路段失效将直接影响路网总阻抗的变化,进而影响整个路网的网络效率及其鲁棒性。在上述算例中,识别出的路网最脆弱区域为:路段20(128.31 h·veh)、路段21(58.398 h·veh)、路段2(24.427 h·veh)、路段5(11.798 h·veh)等,亦均为对网络效率与鲁棒性影响较大的路段,影响量分别为6.94%,6.79%,6.63%,6.50%。
但是,对算例路网的鲁棒性分析与脆弱性识别结果仍有差异, 如表 3所示。
| 相关路段 | 主要差异 |
| 10 | 路网总阻抗变化量较大,但对路网鲁棒性影响较小 |
| 4,19 | 路网总阻抗变化量较小,但对路网鲁棒性影响较大 |
| 6,14 | 鲁棒性分析与脆弱性识别排序结果相反 |
表 3中,路段10失效后对整个路网运输效率影响排序靠后,为4.08%,但经脆弱性识别发现,该路段在发生突发拥挤时对整个路网的总阻抗变化量影响很大,为96.496 h·veh;路段4和路段19在失效后,整个路网的总阻抗基本不变,而这两个路段对网络鲁棒性仍有影响,分别为4.32%与3.85%;路段6和路段14,按鲁棒性分析结果,路段6影响大小为4.63%,排序第5位,路段14影响大小为4.55%,排序第6位,而按脆弱性识别结果,路段6仅为5.965 h·veh,排序第7位,路段14却为11.798 h·veh,排序第6位,排序结果恰恰相反。
这说明:(1) 在考虑路段排队容量限制后,路网的脆弱性不仅与其鲁棒性等有关,潜在交通流量向阻抗较小路段转移和突发拥挤导致车辆排队溢出影响路段阻抗增大等因素,均对路网脆弱性有显著影响。(2) 如果拥堵路段具有较大的容量限制(如车道数较多、道路容量较大等),能够容纳相当数量的交通量,从而可在一定程度上缓解突发拥挤的扩散效应,尽量保证路网的运输效率与鲁棒性不受事发路段突发拥挤的影响。
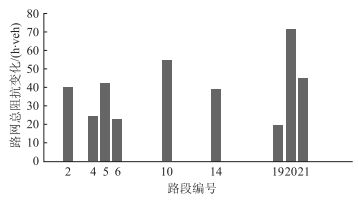
此外,本文还利用传统的无约束交通网络配流方法对算例进行了对比验证,此方法下路网G′(N′, L′)中各路段的脆弱性指标Δca的大小如图 7所示。
|
| 图 7 无约束条件下各路段Δca值的变化 Fig. 7 Change of Δca of each road section without constraint |
| |
从图 7可以看出,无约束条件下完成的网络配流结果存在明显的路段聚类现象,即同类中Δca值大小相近,而不同类之间Δca值差异明显。故将无约束条件下的各路段脆弱性识别排序结果与考虑路段排队容量的脆弱性识别结果进行比较,如表 4所示。
从表 4得出,从排序结果来看,两种方法对关键路段(路段10、路段20、路段21等)的识别结果一致,但考虑排队容量约束的脆弱性识别方法更能凸显关键路段的差异性,而利用无约束条件下的识别方法,同类中各路段的Δca值差异很小,无法合理反映出路网中脆弱路段对网络鲁棒性的影响,误判可能性较大。
| 排序 | 无约束条件 | 考虑排队容量约束 | ||
| 路段编号 | Δca/(h·veh) | 路段编号 | Δca/(h·veh) | |
| 1 | 20 | 71.727 | 20 | 128.310 |
| 2 | 10 | 54.513 | 10 | 96.496 |
| 3 | 21 | 45.188 | 21 | 58.398 |
| 4 | 5 | 42.477 | 2 | 24.427 |
| 5 | 14 | 39.928 | 5 | 11.798 |
| 6 | 2 | 39.130 | 14 | 11.798 |
| 7 | 4 | 24.405 | 6 | 5.965 |
| 8 | 6 | 22.941 | 4 | 0.489 |
| 9 | 19 | 19.500 | 19 | 0.062 |
5 结论
根据上述分析建模与算例论证,得出突发拥挤条件下的城市道路网脆弱性分析相关结论如下:
(1) 改进了定量识别城市路网关键路段的分析方法,在进行路网脆弱性分析与识别之前,先完成了路网的鲁棒性分析,利用点的连通度与边的网络效率等指标量化了突发拥挤交叉口或路段的失效对路网运输效率的影响,可从中观层面得到路网中潜在的关键路段。
(2) 考虑了潜在关键路段的排队容量限制,通过构建带路段容量约束的交通网络配流模型,以突发拥堵前后的路网总阻抗变化率大小作为脆弱性识别指标,设计算例,论证得到路网鲁棒性与脆弱性的关系与差异。
(3) 从城市道路复杂网络特性入手,利用遍历法逐一量化计算路段的交通流量变化,将单一路段或交叉口作为研究重点。考虑道路突发事件可能造成的多个交叉口或路段同时发生拥堵的情况,以及拥堵信息传播对潜在道路交流量的影响,将是下一阶段的研究方向。
| [1] | JENELIUS E, PETERSEN T, MATTSSON L G. Importance and Exposure in Road Network Vulnerability Analysis[J]. Transportation Research Part A: Policy & Practice, 2006, 40(7): 537-560 |
| [2] | D'ESTE G M, TAYLOR M A P. Network Vulnerability: An Approach to Reliability Analysis at the Level of National Strategic Transport Networks[C]//Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR). New York: Pergamon Press, 2003:23-44. |
| [3] | 赵玲, 邓敏, 王佳璆, 等. 应用复杂网络理论的城市路网可靠性分析[J]. 测绘科学, 2013, 38(3): 83-86 ZHAO Ling, DENG Min, WANG Jia-qiu, et al. Reliability Analysis of Urban Street Network Based on Complex Network Theory[J]. Science of Surveying and Mapping, 2013, 38(3): 83-86 |
| [4] | 董洁霜, 吴雨薇, 路庆昌, 等. 降雨条件下城市道路网络拓扑结构脆弱性分析[J]. 交通运输系统工程与信息, 2015, 15(5): 109-114 DONG Jie-shuang, WU Yu-wei, LU Qing-chang, et al. Road Network Topology Vulnerability Indentification Considering the Intensity of Rainfall in Urban Areas[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(5): 109-114 |
| [5] | SCOTT D M, NOVAK D C, AULTMAN-HALL L, et al. Network Robustness Index: A New Method for Identifying Critical Links and Evaluating the Performance of Transportation Networks[J]. Journal of Transport Geography, 2006, 14(3): 215-227 |
| [6] | SULLIVAN J L, NOVAK D C, AULTMAN-HALL L, et al. Identifying Critical Road Segments and Measuring System-wide Robustness in Transportation Networks with Isolating Links: A Link-based Capacity-reduction Approach[J]. Transportation Research Part A: Policy & Practice, 2010, 44(5): 323-336 |
| [7] | 肖瑶. 基于复杂网络理论的城市道路网络综合脆弱性评估模型[D]. 武汉: 华中科技大学, 2013. XIAO Yao. An Integrative Vulnerability Evaluation Model for Urban Road Network Based on Complex Network Theory[D]. Wuhan: Huazhong University of Science and Technology, 2013. |
| [8] | 张勇, 屠宁雯, 姚林泉. 城市道路交通网络脆弱性识别方法[J]. 中国公路学报, 2013, 26(4): 154-161 ZHANG Yong, TU Ning-wen, YAO Lin-quan. Urban Road Traffic Network Vulnerability Identification Method[J]. China Journal of Highway and Transport, 2013, 26(4): 154-161 |
| [9] | NGUYEN S, DUPUIS C. An Efficient Method for Computing Traffic Equilibria in Networks with Asymmetric Transportation Costs[J]. Transportation Science, 1984, 18(2): 185-202 |
| [10] | 卢顺达. 交通管控条件下拥堵交通网络配流分配模型及算法[D]. 南京: 东南大学, 2015: 17-28. LU Shun-da. Traffic Assignment Model and Algorithm with Traffic Management and Control for Congested Network[D], Nanjing: Southeast University, 2015:17-28. |
| [11] | 张雄飞, 李瑞敏, 郭旭明, 等. 带转向延误的拥挤交通网络配流模型及算法[J]. 清华大学学报:自然科学版, 2012, 52(6): 848-853 ZHANG Xiong-fei, LI Rui-min, GUO Xu-ming, et al. Traffic Assignment Problem Model with Turning Delays for Congested Networks[J]. Tsinghua University: Science and Technology Edition, 2012, 52(6): 848-853 |
| [12] | 赵国锋, 苑少伟, 慈玉生. 城市路网的复杂网络特性和鲁棒性研究[J]. 公路交通科技, 2016, 33(1): 119-124 ZHAO Guo-feng, YUAN Shao-wei, CI Yu-sheng. Analysis of Complex Network Property and Robustness of Urban Road Network[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 119-124 |
| [13] | 张勇, 杨晓光. 城市路网的复杂网络特性及可靠性仿真分析[J]. 系统仿真学报, 2008, 20(2): 464-513 ZHANG Yong, YANG Xiao-guang. Complex Network Property and Reliability Simulation Analysis of Urban Street Networks[J]. Journal of System Simulation, 2008, 20(2): 464-513 |
| [14] | ALBERT R, JEONG H, BARABASI A L. Error and Attack Tolerance of Complex Network[J]. Nature, 2000, 409(6819): 378-382 |
| [15] | 吴建军, 高自友. 城市交通复杂性:复杂网络方法及其应用[M]. 北京: 科学出版社, 2010: 24-30. WU Jian-jun, GAO Zi-you. Urban Traffic Complexity: Complex Network Method and Its Application[M]. Beijing: Science Press, 2010: 24-30. |
| [16] | 陆化普, 黄海军. 交通规划理论研究前沿[M]. 北京: 清华大学出版社, 2007. LU Hua-pu, HUANG Hai-jun. Theoretical Research Frontiers in Transportation Planning[M]. Beijing: Tsinghua University Press, 2007. |
 2017, Vol. 34
2017, Vol. 34
