扩展功能
文章信息
- 刘钊, 杜威, 闫冬梅, 柴干, 郭建华
- LIU Zhao, DU Wei, YAN Dong-mei, CHAI Gan, GUO Jian-hua
- 基于K近邻算法和支持向量回归组合的短时交通流预测
- Short-term Traffic Flow Forecast Based on Combination of K Nearest Neighbor Algorithm and Support Vector Regression
- 公路交通科技, 2017, 34(5): 122-128, 158
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(5): 122-128, 158
- 10.3969/j.issn.1002-0268.2017.05.017
-
文章历史
- 收稿日期: 2016-05-03
智能交通系统被认为是缓解城市道路拥堵、减少汽车污染、防治交通事故以及实现节约能源等问题的有效方法。其中,作为智能交通系统重要基础之一的短时交通流预测,是实时、准确、快速实现交通管理、诱导及控制的关键[1]。因此,对短时交通流预测方法的研究具有重要的意义。
目前,可用于交通流预测的模型与方法有很多,常用的方法如历史平均[2]、时间序列[3]及卡尔曼滤波[4]等基于确定数学模型的方法,以及基于神经网络[5]、小波理论[6]、非参数回归[7]、支持向量机[8]等非线性理论的预测方法。针对交通流数据的应用,Guo等[9]研究了不同时间间隔条件下交通流率数据的特性,表明时间序列方法更适用于时间间隔大于10 min的交通流预测。此外,针对不同预测模型或预测方法的特点,还提出了组合预测方法。例如,孙占全等[10]提出用支持向量机与主成分分析相结合的交通流预测方法,该组合预测方法可以提高预测精度,降低预测所需的计算量,并且满足交通流预测的实时性要求;樊娜等[11]把非参数回归方法和BP神经网络相结合,采用模糊控制算法确定各单项模型的权重,并按不同权重组合成新的混合预测模型;沈国江等[12]提出了一个包含卡尔曼滤波、神经网络和模糊综合模型3个子模型相组合的预测模型,应用结果表明提出的组合预测模型能够发挥各自子模型的优势。黄玲等[13]提出了一种基于移动检测技术、神经网络和模糊判断方法的城市路网动态交通拥挤预测模型;Wang等[14]利用小波理论构建了一个新的核函数以捕捉短时交通速度数据的非平稳特性,并运用支持向量机进行了预测。由于现实中交通系统的不确定性、非线性和复杂性,相对于基于确定数学模型的预测方法,基于启发式的预测方法由于不需要构建复杂的数学模型,并且预测精度也能满足智能交通系统的要求,因此具有一定的优势。
在众多基于启发式的非线性理论预测方法中,神经网络凭借其逼近任意非线性函数的能力和自学习等优点被广泛使用。然而基于经验风险最小原则的神经网络,其结构选择缺乏理论指导,容易陷入局部极值点,因此神经网络的鲁棒性受到限制[15]。相对而言,支持向量机具有完备的理论基础和出色的学习性能,不存在局部最小问题,并且运用核函数解决维数问题,具有较强的鲁棒性[16]。不同于需要大量训练数据的神经网络,支持向量机则需要少量的训练数据。此外,与这两种需要利用历史数据进行模型训练的方法相比较,K近邻非参数回归法具有算法简单清晰、移植应用性好等优势[17],因此该方法可以与其他预测方法相结合,发挥组合模型的优势。
为此,本文提出一种基于非参数回归与支持向量机相结合的短时交通流预测方法,该方法利用K近邻非参数回归法的搜索机制,重构历史交通流时间序列,并利用重构的历史交通流数据对支持向量机进行训练,以此提高短时交通流预测的精度。针对实际的交通流数据,利用本文提出的组合预测方法,分别构建基于时间维度和时空维度状态向量的预测模型,通过与传统预测方法的比较,验证分析其有效性。
1 K近邻非参数搜索机制非参数回归方法,是通过搜索历史数据库与当前观测值相似的数据来进行预测。与一般解析方法不同,理论上看,它是一种模式识别的方法,不是在系统输入和输出之间找到1个精确的函数对应关系,而是利用模式匹配算法找到1组与输入数据相对应的数据,而对应关系不需要精确的函数表达式,而是1个近似的关系,甚至这个近似的关系都不是必须的[17]。
本文利用K近邻非参数回归的模式匹配算法,重构与当前时刻相似的历史交通流时间序列,把重构的交通流时间序列应用到支持向量回归方法中。有关详细的支持向量回归预测原理可以参考文献[18]。
1.1 状态向量状态向量是进行当前数据与历史数据比较的标准,对状态向量的选取没有统一的标准,把尽可能多的因素考虑到状态向量中并不能提高预测精度,反而会导致较长时间的算法运行时间。如何选择合适的状态向量,往往根据具体的实际情况而定。
由于交通流具有时间相关性和空间相关性,因此在进行状态向量的构建时,通常考虑时间维度和时空维度因素的影响。前者只考虑预测路段断面的交通信息时间序列,而后者则兼顾考虑预测断面及其上下游的交通信息状态。相关研究也表明,上下游的交通状态变化会对预测路段产生影响。
1.2 距离度量方式距离度量是用于度量历史数据库中各个样本状态向量与当前状态向量的近似程度。目前多种距离度量方式可用于K近邻的搜索,例如切比雪夫距离、马氏距离、欧式距离等等。但当K近邻非参数回归用于短时交通流的预测时,通常采用的是欧式距离作为度量指标。

|
(1) |
式中,di为当前时刻与历史数据库中某时刻状态向量的距离;Vi为当前时刻第i个子项的数值;
近邻值K的选取,表示从历史数据库中选取与当前状态向量距离最近的K个状态向量。K值的选取在很大程度上与历史数据的具体情况及状态向量的具体构成有关。目前还没有相关的规则来指导K值的选取,已有的相关文献均是针对各自具体的试验数据,根据具体的状态向量,选取最优的K值。一般而言,在利用非参数回归方法进行短时交通流预测时,预测精度首先会随着K值的增加而逐渐提高,随后趋于稳定,然后随着K值的继续增加预测精度会下降。总之,K值过大或过小都将影响预测精度。
2 基于KNN-SVR短时交通流预测建模 2.1 模型的构建短时交通流预测是一种应用性很强的技术,即根据路段的交通流量历史数据,采用一定的方法建立合适的数学模型,从而求出路段未来时刻的交通流量状态估计值。根据K近邻方法(KNN)和支持向量回归(SVR)算法的特点,本文把这两种方法结合在一起,提出KNN-SVR的预测模型,该模型利用K近邻非参数回归的搜索特点,重建历史交通流的时间序列,并利用重建的历史交通流数据训练SVR模型,通过提升训练数据与当前交通流状态的相似程度,来获取更好的回归结果,从而提高短时交通流的预测精度。组合预测模型KNN-SVR的框架如图 1所示。

|
| 图 1 KNN-SVR建模过程 Fig. 1 KNN-SVR modeling process |
| |
如图 1所示,在KNN-SVR模型的建模过程中,存在3个重要的参数,它们的取值将直接影响模型的预测性能。其中,在KNN模型中,K值为从历史数据库中选取的近邻数,它的取值将决定构建训练数据集的大小。K值越大,即从历史数据库中选取的近邻数就越多,然而选取越多的近邻,构建的训练数据与当前交通状态的近似程度将会越低,这将会降低训练数据的质量,影响SVR的训练效果。在SVR模型中,参数C和ε分别表示惩罚因子和不敏感损失函数,它们会直接影响SVR进行网络训练的效果,即影响回归计算的精度。在KNN-SVR模型中,这3个参数之间可能存在相互影响的关系。
2.2 模型参数的确定在KNN-SVR模型中,主要有3个参数需要确定。即在利用KNN构建SVR训练数据集时所用的近邻值K,以及在SVR模型中构建分类超平面时所用的惩罚因子C和不敏感损失函数ε。单独使用KNN或SVR模型时,均没有既定的准则来指导相关参数的选取,已有文献也是针对各自的试验数据选取最优的参数值。
为了确定KNN-SVR模型的最优参数取值,首先针对近邻搜索机制,将K值的取值范围设定在1~40之间。然后针对SVR的训练过程,采用基于交叉验证的网格划分搜索方法确定参数C和ε的取值,即划定参数的选择值域,并在该值域范围内搜索,得到回归结果最好的参数取值。通过逐一比较SVR的训练结果,确定K,C,ε这3个参数的最佳取值。
为了确定参数C和ε的最佳取值,采用交叉验证的方法,即将原始数据平均分成K组,将每个子集数据分别做一次验证集,其余的K-1组子集数据作为训练数据,这样就会得到K个模型,用这K个模型最终验证集的回归准确率的平均值作为最终的性能指标。这样,可以有效避免过学习以及欠学习状态的发生,最后得到的回归结果也具有较强的说服性。相关研究表明,采用交叉验证选取出的参数训练SVM得到的模型比随机选取参数训练SVM得到的模型在分类上更有效果[18]。具体的寻优结果将会针对试验结果进行分析讨论。
2.3 预测误差指标针对模型参数C和ε的确定过程,采用均方误差作为评价指标。而对于预测结果的误差评价,常用的评价指标是平均绝对百分比误差和均方根误差。
(1) 均方误差
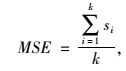
|
(2) |
式中,si为第i组的均方误差;k为把用于验证的原始数据平均划分的组数。
(2) 平均绝对百分比误差

|
(3) |
式中,n为测试样本数;yi为测试样本值;
(3) 均方根误差:

|
(4) |
式(2) 用于参数C和ε的交叉验证,而式(3) 和式(4) 则用于预测结果的误差评价。
3 实例分析 3.1 试验设计实例所采用的数据来自于美国波特兰快速路Ⅰ-25上的线圈数据。由于各个路段上交通流量有较大差异,同时兼顾试验数据的充足性和原始数据的质量两方面的因素,本文选取了数据质量良好的连续5个断面的线圈数据作为试验数据,并且选择其中连续的3个断面作为预测研究对象。数据的采集时间为2011年10月1日~10月8日,数据的统计输出间隔为5 min。其中采用10月1日~10月7日的数据作为KNN搜索匹配的历史数据库,10月8日的288个数据作为测试数据。
由于在构造状态向量时,一般选取与预测对象最为相关的因素,根据文献[2]中的K近邻方法框架,考虑本文获得交通数据的具体情况,设置两组状态向量, 分别考虑时间维度和时空维度的影响:
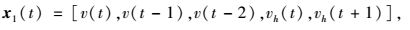
|
(5) |

|
(6) |
式中,v(t)表示目标断面在t时刻的交通流量;vh(t)表示目标断面在历史数据库中t时刻的交通流量,v-1(t)表示目标断面上游在t时刻的交通流量,v+1(t)表示目标断面下游在t时刻的交通流量。其中,式(5) 只考虑了时间维度的状态,而式(6) 同时考虑了时间维度和空间维度的状态。
为了验证本文提出的KNN-SVR模型的有效性,选取非参数回归模型、支持向量回归模型及反向传播神经网络(Back-propagation Neural Networks, BPNN)模型进行对比研究,分别考虑时间维度和时空维度的影响,构建具体的预测模型,如表 1所示。
| 编号 | 状态向量 | 临近路段(上游+下游) | 时间因素 |
| KNN1 | 时间维度 | √ | |
| KNN2 | 时间+空间维度 | √ | √ |
| SVR1 | 时间维度 | √ | |
| SVR2 | 时间+空间维度 | √ | √ |
| BPNN1 | 时间维度 | √ | |
| BPNN2 | 时间+空间维度 | √ | √ |
| KNN-SVR1 | 时间维度 | √ | |
| KNN-SVR2 | 时间+空间维度 | √ | √ |
| 注: KNN1为KNN采用仅考虑时间维度的状态向量x1(t)建立的模型;KNN2为KNN采用考虑时间和空间维度的状态向量x2(t)建立的模型;同样对于SVR, BPNN, KNN-SVR,均分别采用x1(t)和x2(t)来建立具体的预测模型;√表示在建立具体预测模型的状态向量时所选择考虑的因素。 | |||
利用欧拉距离度量方式,搜索匹配与当前交通流临近的K个状态向量。近邻值K的选取在很大程度上与历史数据的具体情况相关。在本文中,设置近邻值K的值域范围是[2, 40]。同时,分别以C和ε为底取对数,构建搜索空间log2C∈[-8, 8]和log2ε∈[-8, 8],即C∈[2-8, 28],ε∈[2-8, 28]。针对每个K值,在构建的搜索空间中,实现参数C和ε的选取。具体参数寻优结果将在模型参数分析中进行讨论。
3.2 模型参数分析针对构建的BPNN模型,采用3层的网络结构,即输入层、隐含层及输出层。其中,输入层的变量即为状态向量。参考关于隐含层节点的影响分析[19],把隐含层节点数设为20,并且选择LM作为神经网络的训练函数[20]。
现主要对KNN-SVR中所涉及的3个参数进行分析。本文主要通过搜索寻优的方法来确定最优参数。其中针对SVR模型中的C和ε,采用网格划分的方法来搜索最佳的参数。与传统的KNN和SVR模型相比,无论是仅考虑时间维度的状态向量,还是同时考虑时间维度和空间维度的状态向量,KNN-SVR模型在参数寻优过程中,均体现出更好的模型性能。现以断面1的交通流量预测为例,分析KNN-SVR模型中参数的影响。首先分析针对参数C和ε的交叉验证过程,如图 2所示。

|
| 图 2 参数C和ε对预测模型的影响 Fig. 2 Impact of C and ε on prediction models |
| |
在图 2中,针对参数C和ε的搜索寻优,对比了SVR与KNN-SVR模型的训练性能。从整个搜索过程中可以看出,相比SVR模型而言,KNN-SVR模型在C和ε的搜索范围内拥有更稳定、更高的性能。并且与仅考虑预测路段的交通流相比,同时考虑预测路段交通流和邻近路段交通流影响的模型在参数搜索中均呈现更好的预测性能。这说明,使用经过KNN搜索机制构造的训练数据进行训练的SVR,拥有更高的预测精度和鲁棒性,即预测精度对参数C和ε的变化不敏感。针对仅考虑时间维度的KNN-SVR1模型,参数C和ε最佳的搜索区域是log2C∈[0, 2]和log2ε∈[0, 2];而针对考虑时间维度和空间维度的KNN-SVR2模型,参数最佳的搜索区域则是log2C∈[0, 2]和log2ε∈[0, 2]。
在针对参数C和ε交叉验证搜索的基础上,进一步分析近邻值K的影响,如图 3所示。

|
| 图 3 近邻值K对预测模型的影响 Fig. 3 Impact of nearest-neighbor value K on prediction models |
| |
图 3比较了KNN模型与KNN-SVR模型中近邻值K的影响。对KNN与KNN-SVR这两个模型,与仅考虑时间维度的状态相比,同时考虑时间维度和空间维度的状态均呈现出更好的预测性能。在图 3(a)中,对于传统的KNN方法,仅考虑时间维度的预测模型KNN1,与同时考虑时间维度和空间维度的预测模型KNN2,它们的预测精度均随着K值的增加而提高,逐渐趋于稳定,并且后者的预测精度MAPE总是优于前者大约1%;而在图 3(b)中,仅考虑时间维度的预测模型KNN-SVR1,与同时考虑时间维度和空间维度的预测模型KNN-SVR2,它们的预测精度均随着K值的增加而逐渐降低,当K值小于20时,KNN-SVR2模型的预测精度明显高于KNN-SVR1的预测精度,这说明在预测过程中,上下游路段的交通状况对目标路段交通状况的影响也很重要,并且考虑预测路段上下游交通状态的影响,可以提高模型的预测精度。对比图 3(a)和(b)可以看出,KNN-SVR模型对参数K的取值较为敏感。
针对KNN,SVR,KNN-SVR这3个预测模型,分别给出了各模型参数最优的选择结果,如表 2所示。
| 模型编号 | 断面1 | 断面2 | 断面3 | ||||||
| K | C | ε | K | C | ε | K | C | ε | |
| KNN1 | 12 | — | — | 21 | — | — | 27 | — | — |
| KNN2 | 30 | — | — | 34 | — | — | 36 | — | — |
| SVR1 | — | 9.19 | 0.06 | — | 27.86 | 0.02 | — | 21.11 | 0.14 |
| SVR2 | — | 27.86 | 0.02 | — | 5.28 | 0.06 | — | 9.19 | 0.06 |
| KNN-SVR1 | 5 | 3.03 | 1.74 | 7 | 3.03 | 0.92 | 1 | 256 | 0.01 |
| KNN-SVR2 | 3 | 1.74 | 0.19 | 8 | 1.00 | 1.00 | 2 | 9.20 | 0.11 |
3.3 预测精度分析
针对试验设计中提出的预测模型,利用实际交通流量数据,应用各个预测模型对未来交通流进行预测。各预测模型的具体预测精度分别如图 4和图 5所示。

|
| 图 4 不同断面预测精度(MAPE)比较 Fig. 4 Comparison of prediction accuracy (MAPE) at different sections |
| |

|
| 图 5 不同断面预测精度(RMSE)比较 Fig. 5 Comparison of prediction accuracy (RMSE) at different sections |
| |
图 4和图 5对比了不同预测模型在3个不同断面的短时交通流预测精度。可以看出,首先,针对KNN,SVR,KNN-SVR这3个预测模型,同时考虑上下游路段交通状态的预测模型要优于只考虑目标路段交通状态的预测模型。并且对于SVR而言,引入空间维度参数在3个断面的预测中可以提高大约3%的精度。而对于BPNN而言,随着引入上下游路段的空间维度参数,反而使得预测精度有所降低。其次,KNN与KNN-SVR在3个断面的预测精度较高,MAPE均为10%左右。而SVR和BPNN的预测精度则较差,特别是在断面3,MAPE超过了20%。相比而言,对于路段的交通状况,KNN模型和KNN-SVR模型拥有较好的预测稳定性。不同预测模型平均预测结果如表 3所示。
| KNN1 | KNN2 | SVR1 | SVR2 | BPNN1 | BPNN2 | KNN- SVR1 | KNN- SVR2 | |
| MAPE/% | 10.27 | 9.75 | 16.51 | 13.53 | 16.26 | 16.99 | 9.16 | 8.29 |
| RMSE | 81.08 | 72.77 | 133.71 | 106.83 | 131.80 | 137.86 | 75.66 | 73.52 |
表 3对比了不同预测模型的平均预测精度指标。KNN-SVR的预测精度最高,考虑了时间维度和时空维度预测模型的平均MAPE分别为9.16%和8.29%,RMSE分别为75.66,73.52 veh/(h·lane)。相比KNN-SVR而言,KNN模型的预测精度则略低。而SVR和BPNN模型的预测效果均不甚理想。总的来说,比较不同预测模型在3个断面的预测精度,KNN-SVR的预测性能优于其他几种模型。
4 结论本文结合非参数回归与支持向量回归方法的特点,建立了一个组合的短时交通流预测KNN-SVR模型。该组合模型利用K近邻非参数回归的搜索机制,重构交通流的历史时间序列,并作为SVR的训练数据。通过构建与当前交通流状态近似的训练数据,提升SVR模型的回归效果,达到提高预测精度的目的。为了验证本文提出组合预测方法的有效性,采用实际交通流数据,构建了具体的预测模型,对3个断面的交通流进行了预测。与传统单一的KNN,SVR,BPNN模型相比,本文提出的KNN-SVR预测模型具有较高的预测精度,其预测误差均在10%以内,更适合对道路短时交通流进行实时、准确的预测。在后续研究中,将针对该混合预测模型,实现在线的短时交通流预测,并且对该混合预测模型进行优化,进一步减小预测误差,提高运算效率与预测精度。
| [1] | VLAHOGIANNI E I, GOLIAS J C, KARLAFTIS M G. Short-term Traffic Forecasting: Overview of Objectives and Methods[J]. Transport Reviews, 2004, 24(5): 533-557 |
| [2] | SMITH B L, WILLIAMS B M, OSWALD R K. Comparison of Parametric and Nonparametric Models for Traffic Flow Forecasting[J]. Transportation Research Part C: Emerging Technologies, 2002, 10(4): 303-321 |
| [3] | KARLAFTIS M G, VLAHOGIANNI E I. Memory Properties and Fractional Integration in Transportation Time Series[J]. Transportation Research Part C: Emerging Technologies, 2009, 17(4): 444-453 |
| [4] | GUO J H, WILLIAMS B M. Real Time Short Term Traffic Speed Level Forecasting and Uncertainty Quantification Using Layered Kalman Filters[J]. Transportation Research Record, 2010, 2175: 28-37 |
| [5] | 宋国杰, 胡程, 谢昆青, 等. 面向实时短时交通流预测的过程神经元网络建模[J]. 交通运输工程学报, 2009, 9(5): 73-77 SONG Guo-jie, HU Cheng, XIE Kun-qing, et al. Process Neural Network Modeling for Real Time Short-term Traffic Flow Prediction[J]. Journal of Traffic and Transportation Engineering, 2009, 9(5): 73-77 |
| [6] | 杨春霞, 符义琴, 鲍铁男. 基于相似性的短时交通流预测[J]. 公路交通科技, 2015, 32(10): 124-128 YANG Chun-xia, FU Yi-qin, BAO Tie-nan. Short-term Traffic Flow Prediction Based on Similarity[J]. Journal of Highway and Transportation Research and Development, 2015, 32(10): 124-128 |
| [7] | 张涛, 陈先, 谢美萍, 等. 基于K近邻非参数回归的短时交通流预测方法[J]. 系统工程理论与实践, 2010, 30(2): 376-384 ZHANG Tao, CHEN Xian, XIE Mei-ping. K-NN Based on Nonparametric Regression Method for Short Term Traffic Flow Forecasting[J]. System Engineering-Theory & Practice, 2010, 30(2): 376-384 |
| [8] | WU Q. A Hybrid-forecasting Model Based on Gaussian Support Vector Machine And Chaotic Particle Swarm Optimization[J]. Expert Systems with Applications, 2010, 37(3): 2388-2394 |
| [9] | GUO J, WILLIAMS B M, SMITH B L. Data Collection Time Intervals for Stochastic Short-term Traffic Flow Forecasting[J]. Transportation Research Record, 2008, 2024: 18-26 |
| [10] | 孙占全, 潘景山, 张赞军, 等. 基于主成分分析与支持向量机结合的交通流预测[J]. 公路交通科技, 2009, 26(5): 127-131 SUN Zhan-quan, PAN Jing-shan, ZHANG Zan-jun, et al. Traffic Flow Forecast Based on Combining Principal Component Analysis with Support Vector Machine[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 127-131 |
| [11] | 樊娜, 赵祥模, 戴明, 等. 短时交通流预测模型[J]. 交通运输工程学报, 2012, 12(4): 114-119 FAN Na, ZHAO Xiang-mo, DAI Ming, et al. Short-term Traffic Flow Prediction Model[J]. Journal of Traffic and Transportation Engineering, 2012, 12(4): 114-119 |
| [12] | 沈国江, 王啸虎, 孔祥杰. 短时交通流量智能组合预测模型及应用[J]. 系统工程理论与实践, 2011, 31(3): 561-568 SHEN Guo-jiang, WANG Xiao-hu, KONG Xiang-jie. Short-term Traffic Volume Intelligent Hybrid Forecasting Model and its Application[J]. System Engineering-Theory & Practice, 2011, 31(3): 561-568 |
| [13] | 黄玲, 林培群, 徐建闽. 基于移动检测技术的城市路网拥挤预测模型[J]. 公路交通科技, 2009, 26(10): 121-125 HUANG Ling, LIN Pei-qun, XU Jian-min. Urban Road Network Traffic Congestion Prediction Model Based on Probe Vehicle Technology[J]. Journal of Highway and Transportation Research and Development, 2009, 26(10): 121-125 |
| [14] | WANG J, SHI Q. Short-term Traffic Speed Forecasting Hybrid Model Based on Chaos-wavelet Analysis-support Vector Machine Theory[J]. Transportation Research Part C: Emerging Technologies, 2013, 27: 219-232 |
| [15] | 向小东. 基于神经网络与混沌理论的非线性时间序列预测研究[D]. 成都: 西南交通大学, 2002. XIANG Xiao-dong. Research on Forecast of Nonlinear Time Series Based on Neural Networks and Chaotic Theory[D]. Chengdu: Southeast Jiaotong University, 2002. |
| [16] | 杨兆升, 王媛, 管青. 基于支持向量机方法的短时交通流量预测方法[J]. 吉林大学学报:工学版, 2006, 36(6): 881-884 YANG Zhao-sheng, WANG Yuan, GUAN Qing. Short-term Traffic Flow Prediction Method Based on SVM[J]. Journal of Jilin University: Engineering and Technology Edition, 2006, 36(6): 881-884 |
| [17] | 张晓利, 陆化普. 非参数回归方法在短时交通流预测中的应用[J]. 清华大学学报:自然科学版, 2009, 49(9): 1471-1475 ZHANG Xiao-li, LU Hua-pu. Non-parametric Regression for Short-term Traffic Flow Forecasting[J]. Journal of Tsinghua University: Science and Technology Edition, 2009, 49(9): 1471-1475 |
| [18] | SMOLA A J, SCHÖLKOPF B. A Tutorial on Support Vector Regression[J]. Statistics and Computing, 2004, 14(3): 199-222 |
| [19] | YUAN F, CHEU R L. Incident Detection Using Support Vector Machines[J]. Transportation Research Part C: Emerging Technologies, 2003, 11(3): 309-328 |
| [20] | TAN M C, WONG S C, XU J M, et al. An Aggregation Approach to Short-term Traffic Flow Prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(1): 60-69 |
 2017, Vol. 34
2017, Vol. 34
