扩展功能
文章信息
- 魏中华, 李志, 周晨静, 邱实, 徐天宇
- WEI Zhong-hua, LI Zhi, ZHOU Chen-jing, QIU Shi, XU Tian-yu
- 城市快速路合流区汇入角度对合流区通行能力的影响
- Effect of Merge Angle on Capacity of Urban Expressway Merge Area
- 公路交通科技, 2017, 34(5): 116-121
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(5): 116-121
- 10.3969/j.issn.1002-0268.2017.05.016
-
文章历史
- 收稿日期: 2016-05-11
合流区的通行能力是影响快速路通行能力的重要因素之一。城市快速路出入口数量多、间距小,尤其在早、晚高峰期间,大量车辆进出快速路,使合流区成为瓶颈,从而引发交通拥堵,导致快速道路的功能受到制约,甚至导致交通事故[1]。因此,对合流区的通行能力和车辆运行特性进行研究,对保证车辆畅通运行、提高交通安全,充分发挥快速路的功能具有重要意义。
目前国内对快速路合流区的通行能力进行的研究较少[2],成果不多,特别是快速路合流区汇入角度对合流区通行能力的影响研究,研究成果缺乏一定的理论基础[3]。本文通过现场调研数据并进行分析,建立不同角度汇入合流区的速度流量模型,对城市快速路合流区通行能力的相关参数标定奠定了基础。
1 合流区数据采集 1.1 调研思路利用电子地图标出北京环路所有合流区,并进行类型划分;测量各个合流区汇入角度;根据整理的数据确定调查地点,进行预调研;制定正式的数据采集方案,进行数据采集。
1.2 合流区的分类首先,在电子地图上找出北京市三环、四环、五环的合流区。其次,按照不同汇入角度,将北京市环路的合流区进行汇总。再次,将合流区分为有加速车道和无加速车道两类。数据处理结果显示,北京市快速路共有70余个合流区,其中有加速车道的合流区共有70多个,而无加速车道的合流区仅有4个[4]。
将70余个合流区汇入角度利用auto-cad软件测量后进行汇总,根据数据分析,处理结果如图 1和图 2所示。

|
| 图 1 测量汇入角度示意图 Fig. 1 Schematic diagram of measured merge angle |
| |
|
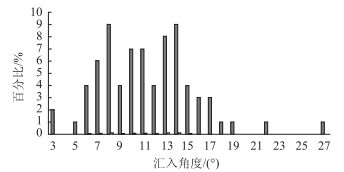
| 图 2 各种汇入角度所占比例 Fig. 2 Proportions of various merge angles |
| |
1.3 调研地点确定和预调研
根据上述测量结果可知,汇入角度主要集中在6°~17°。其中有加速车道的合流区所占比例为95%,所以有加速车道的合流区是主要研究对象。北京市交通委路况交通眼显示,最为拥堵的快速路合流区有12个,其中无加速车道出入口间距为1 200 m、汇入角度为3度的合流区2个。其中有加速车道出入口间距为1 200 m、加速车道长度为130 m的合流区4个,汇入角度分别为5°,8°,13°,18°。选择上述6个合流区作为调查地点,因其出入口间距与加速车道长度固定,固可排除这些因素[5]对通行能力值的影响;相同汇入角度的合流区选择两个主要验证在其他影响条件恒定下,不同地点相同汇入角度的两个合流区对合流区通行能力是否有影响。
为了确定1.2节合流区分类测量的准确性,分别针对上述6个地点开展实地预调研,确定仪器布置位置,确定合流区类型划分以及加速车道长度等,从而制定数据采集方案。由预调研可知,方便实测交通流量、行驶速度、车头时距等信息,为现场调研提供调查基础,从而建立速度流量模型,获取不同汇入角度合流区的通行能力值[6]。
1.4 调研内容和方法(1) 交通流量
选取早高峰时间段上午7:00~9:00,分别统计入口匝道与合流区的交通流量,每5 min记录一次流量。采用视频摄像的方法统计合流前、合流后的交通流量;采用人工计数法统计入口匝道的交通流量。因文中主要涉及车型为大型公交车、小型公交车以及小客车,本文中当量系数换算采用公交车车头与车尾通过同一断面时间差与小客车车头与车尾通过同一断面时间差之比。根据自由流行驶状态下,小客车时间差是0.25 s,大型公交车时间差是0.375 s,小型公交车是0.3 s,则当量系数分别为1.5和1.25[7]。
(2) 行驶速度
选取早高峰时间段上午7:00~9:00,分别统计入口匝道与合流区的行驶速度。采用视频摄像机的方法记录合流前、合流后的地点车速,以及匝道的地点车速。地点车速采用平均车长除以车头通过断面与车尾通过同一断面的时间差。每5 min记录一次地点车速的平均值。实测数据包含自由流车速和拥堵车速[8]。
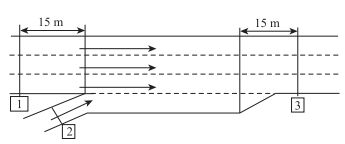
(3) 具体示意图,如图 3所示。
|
| 图 3 合流区布置仪器示意图 Fig. 3 Schematic diagram of layout of measuring devices in merge area |
| |
分别在位置1,2,3放置摄像机,位置1中摄像机主要测量合流前的速度和流量。位置2中摄像机主要测量进入匝道的速度和流量。位置3中摄像机主要测量合流后的速度和流量。从而得到不同汇入角度合流区交通运行的速度-流量图。
1.5 现场调研和数据处理现场调研分为实测匝道、合流前、合流后的速度和流量,根据数据处理结果:可得出如表 1所示不同汇入角度的速度-流量图, 见图 4。
| 匝道 | 合流前 | 合流后 | |||
| 速度/ (km·h-1) | 流量/ (pcu·h-1) | 速度/ (km·h-1) | 流量/ (pcu·h-1) | 速度/ (km·h-1) | 流量/ (pcu·h-1) |
| 40.32 | 672 | 19.512 | 4 068 | 20.7 | 4 680 |
| 28.26 | 864 | 21.024 | 3 564 | 17.46 | 4 320 |
| 36.18 | 852 | 17.28 | 3 792 | 17.64 | 4 428 |
| 32.868 | 708 | 16.38 | 4 212 | 16.74 | 4 296 |
| 26.28 | 852 | 15.336 | 3 960 | 15.768 | 4 452 |
| 20.232 | 960 | 16.272 | 3 672 | 15.156 | 4 272 |
| 19.836 | 948 | 15.3 | 3 600 | 18.288 | 5 472 |
| 30.816 | 948 | 14.688 | 3 636 | 20.952 | 5 220 |
| 23.112 | 780 | 16.02 | 3 816 | 16.128 | 4 644 |
| 25.956 | 816 | 16.776 | 3 792 | 14.868 | 4 176 |
| 23.364 | 924 | 15.336 | 3 708 | 16.452 | 4 344 |
| 29.628 | 768 | 17.172 | 3 744 | 17.136 | 4 632 |
| 23.472 | 960 | 15.048 | 3 708 | 15.3 | 4 428 |
| 20.808 | 900 | 14.328 | 3 348 | 15.444 | 4 524 |
| 25.2 | 936 | 16.488 | 3 852 | 15.768 | 4 176 |
| 27.216 | 672 | 14.616 | 3 336 | 17.604 | 4 548 |
| 35.388 | 792 | 16.704 | 3 492 | 17.208 | 4 332 |
| 25.2 | 804 | 16.416 | 3 840 | 17.136 | 4 272 |
| 40.32 | 672 | 22.14 | 4 212 | 20.34 | 4 383 |
| 28.26 | 864 | 21.06 | 4 383 | 20.52 | 4 653 |
| 36.18 | 852 | 25.308 | 4 788 | 32.796 | 5 976 |
| 32.868 | 708 | 43.128 | 4 437 | 38.124 | 5 139 |
| 26.28 | 852 | 44.352 | 4 788 | 40.32 | 5 103 |
| 20.232 | 960 | 74.52 | 4 419 | 41.472 | 5 706 |
|
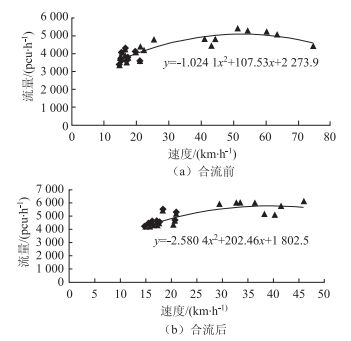
| 图 4 汇入角度为5°速度-流量一元二次多项式 Fig. 4 Speed-volume quadratic polynomial (merge angle of 5°) |
| |
根据表 1可得到汇入角度为5°的合流区匝道、合流前主路、合流后主路断面的速度-流量图, 见图 4。依次类推,按照同样的方法, 分别得到了汇入角度为8°, 13°, 18°的速度-流量数据,从而得到匝道、合流前主路、合流后主路断面的速度-流量拟合曲线。无加速车道的合流区,分别是两个汇入角度为3°的合流区,也得到了相应的速度-流量拟合曲线[9]。
2 合流区数据分析 2.1 通行能力值的推导文中采用修正的Greenshields速度-流量关系模型,速度与流量之间的关系可以简化Q=aV2+bV+c, 其中Q为流量,V为速度,a,b,c为相应参数。将速度-流量关系式进行配方可以得到关系式Q=a(V+b/2a)-b2/4a+c, 当V=-b/2a时,流量最大值Qmax=-b2/4a+c时,这个值便是推导出来的通行能力值[10]。
2.2 有加速车道合流区数据分析 2.2.1 汇入角度为5°合流区数据分析合流前,速度-流量图分析(3车道),如图 4(a)所示。
将速度-流量进行线性回归,得到:
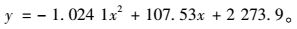
|
从而得到合流前的最大通行能力为5 097 pcu/h,所以单车道通行能力值为1 699 pcu/h/l[10]。
合流后,速度-流量图分析,如图 4(b)所示。
将速度-流量进行线性回归,得到:
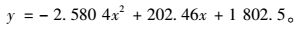
|
从而得到合流前的最大通行能力为5 774 pcu/h,所以单车道通行能力值为1 925 pcu/h/l[7]。
2.2.2 汇入角度为8°, 13°, 18°合流区数据分析有了上述汇入角度为5°的数据分析,按照上述方法分别分析了汇入角度为8°, 13°, 18°的合流区。合流前主路的通行能力值,如表 2所示。
| 汇入角度/ (°) | 通行能力值 | 通行能力公式 | |
| 多车道/ (veh·h-1) | 单车道/ [veh·(h·l)-1] | ||
| 5(3车道) | 5 097 | 1 699 | y=-1.024 1x2+ 107.53x+2 273.9 |
| 8(4车道) | 6 721 | 1 681 | y=-0.847 4x2+ 82.995x+4 687.9 |
| 13(3车道) | 5 142 | 1 714 | y=-1.220 1x2+ 127.22x+1 825.2 |
| 18(4车道) | 6 111 | 1 528 | y=-0.549 3x2+ 34.559x+5 566.6 |
合流后主路的通行能力值,如表 3所示。
| 汇入角度/ (°) | 通行能力值 | 通行能力公式 | |
| 多车道 (veh·h-1) | 单车道/ [veh·(h·l)-1] | ||
| 5(3车道) | 5 775 | 1 925 | y=-2.580 4x2+ 202.46x+1 802.5 |
| 8(4车道) | 7 840 | 1 960 | y=-1.556x2+ 136.82x+4 430.6 |
| 13(3车道) | 5 739 | 1 913 | y=-2.652 7x2+ 211.55x+1 521 |
| 18(4车道) | 7 336 | 1 834 | y=-1.528 4x2+ 123.84x+4 827.4 |
2.3 无加速车道合流区数据分析
同理,按照上述分析方法,得出不同汇入角度合流区上下游主路的通行能力值,如表 4、表 5所示。
2.4 数据整理与分析
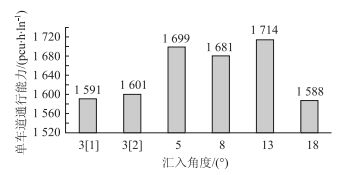
通过视频观测,合流区汇入角度对于合流区的影响不仅局限于最外侧车道,由于车辆存在换道行为等,对于内侧车道通行能力也存在影响,所以本文采取合流区单车道通行能力平均值得出相关结论。由上述数据处理结果得,合流前单车道通行能力对比,如图 5所示。
|
| 图 5 合流区上游单车道通行能力对比 Fig. 5 Comparison of capacity of upstream single lane in merge area |
| |
根据快速路基本路段可能通行能力值可知,当行车速度为80 km/h时,建议取值为1 950 pcu/h/ln[11]。如图 5可知,合流区上游通行能力大小受合流区汇入角度的影响,但两者关系并没有呈现出线性变化趋势。当汇入角度在13°范围内时,合流区上游通行能力达到最大值。原因在于如果合流区汇入角度小于5°时,汇入车流运行视野受限,汇入车辆为保证驾驶安全存在速度降低行为,致使主线通行能力得到降低;如果合流区汇入角度大于18°时,汇入车流运动存在线性上的突变,汇入车辆运行速度也会突然降低,导致主线通行能力降低[12]。同时,可验证在其他因素恒定条件下,不同地点相同汇入角度的合流区通行能力值基本无差别。
为了探究当汇入角度与合流区通行能力的关系,本文应用SPSS软件对于上述数据进行处理,处理结果如表 6所示。选择拟合度为0.845和显著性为0.061的一元二次方程求解,可得出当汇入角度为10.2°时,合流区通行能力值达到最大[13]。
| 公式 | 模型汇总 | 参数估计 | ||||||
| R2 | F | df1 | df2 | Sig. | b1 | b2 | b3 | |
| 一次线性函数 | 0.003 | 0.013 | 1 | 4 | 0.914 | 0.555 | — | — |
| 对数函数 | 0.072 | 0.309 | 1 | 4 | 0.608 | 20.816 | — | — |
| 逆函数 | 0.196 | 0.976 | 1 | 4 | 0.379 | -209.554 | — | — |
| 二次函数 | 0.845 | 8.189 | 2 | 3 | 0.061 | 45.434 | -2.212 | — |
| 三次函数 | 0.846 | 3.666 | 3 | 2 | 0.222 | 50.740 | -2.820 | 0.020 |
| 复合函数 | 0.003 | 0.012 | 1 | 4 | 0.918 | 1.000 | — | — |
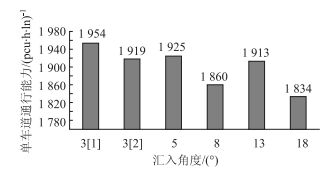
合流后单车道通行能力对比,如图 6所示可知,各种汇入角度的合流区下游通行能力值集中在1 900 pcu/h/l。可见,合流区下游通行能力值与合流区汇入角度无明显相关关系。原因在于车流完成汇入行为之后,便迅速融入主线车流,车流运行速度回归至正常行驶状态,不同汇入角度下,合流区下游主线通行能力表现出统一的取值范畴[14]。
|
| 图 6 合流区下游单车道通行能力对比 Fig. 6 Comparison of capacity of downstream single lane in merge area |
| |
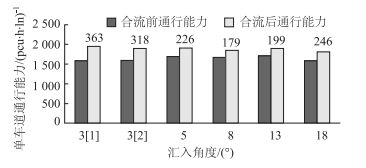
合流前后单车道通行能力对比,如图 7所示。
|
| 图 7 合流区上游和下游单车道通行能力对比 Fig. 7 Comparison of capacity of upstream and downstream single lanes in merge areas |
| |
对于有加速车道的合流区,由于加速车道的存在,致使汇入角度对合流区上下游通行能力影响减小,合流上下游通行能力没有明显差异;而对于无加速车道的合流区,汇入角度对合流区上下游通行能力影响较为明显[15]。造成合流前后通行能力差值较大的原因既有可能是汇入角度不同所致,也可能是加速车道类型不同所致。选取两个汇入3°的合流区,通过与其他汇入角度对比能很好的证明造成通行能力差值较大的原因是加速车道类型不同所致[16]。
3 结论本文通过对北京市环路合流区交通流运行速度调查,获得在不同匝道汇入角度下,合流区交通流运行数据,并处理得出不同汇入角度下合流区在合流区前后断面的通行能力数据[17]。通过以上研究工作,得出以下研究结论:
(1) 合流区上游通行能力大小受合流区汇入角度的影响,但两者关系并不呈现出线性变化趋势。当汇入角度在10.2°时,合流区上游通行能力达到最大值。
(2) 合流区下游通行能力值与合流区汇入角度无明显相关关系。
(3) 对于有加速车道的合流区,由于加速车道的存在致使汇入角度对合流区上下游通行能力影响减小,合流上下游通行能力没有明显差异;而对于无加速车道的合流区,汇入角度对合流区上下游通行能力影响较为明显[18]。
文中因考虑其他影响因素只调查了6个地点,样本量相对较少,深入的研究可在考虑其他因素影响的条件下,调研更多汇入角度对于合流区通行能力的影响。
| [1] | 李秀文. 城市快速路分、合流区通行能力研究[D]. 北京: 北京工业大学, 2005. LI Xiu-wen. Urban Freeway Diverge and Merge Zone Capacity Study [D]. Beijing: Beijing University of Technology, 2005. |
| [2] | 李秀文, 荣建, 刘小明, 等. 快速路分合流影响区交通特性及通行能力研究[J]. 公路交通科技, 2006, 23(1): 101-104 LI Xiu-wen, RONG Jian, LIU Xiao-ming, et al. Analysis of Traffic Flow Characteristics and Capacities of Diverging and Merging Influence Areas[J]. Journal of Highway and Transportation Research and Development, 2006, 23(1): 101-104 |
| [3] | 刘丽琴, 邵长桥, 杨超. 基于匝道控制的快速路合流区通行能力分析[J]. 交通信息与安全, 2013, 31(3): 39-42 LIU Li-qin, SHAO Chang-qiao, YANG Chao. Capacity of Expressway Merging Area Based on Ramp Metering Methodology[J]. Journal of Transport Information and Safety, 2013, 31(3): 39-42 |
| [4] | SARVI M, KUWAHARA M, CEDER A. Traffic Using Simulation Combined with a Driving Simulator[J]. Computer-Aided Civil and Infrastructure Engineering, 2004, 19(5): 351-363 |
| [5] | 王进, 杨晓光. 平面式快速路出入口最小间距研究[J]. 城市交通, 2010, 8(3): 50-57 WANG Jin, YANG Xiao-guang. Minimum Length between Enhance and Exit of Expressway[J]. Urban Transport of China, 2010, 8(3): 50-57 |
| [6] | MARCZAK F, LECLERCQ L, BUISSON C. A Macroscopic Model for Freeway Weaving Sections[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(6): 464-477 |
| [7] | 薛行健. 城市快速路匝道合流区汇入车辆折算系数研究[J]. 重庆交通大学:自然科学版, 2015(1): 95-99 XUE Xing-jian. Research of Vehicle Conversion Coefficients on Urban Expressway Ramp at Merging Area[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2015(1): 95-99 |
| [8] | KIM J T, KIM J K, CHANG M C. Lane-changing Gap Acceptance Model for Freeway Merging in Simulation[J]. Canadian Journal of Civil Engineering, 2008, 35(3): 301-311 |
| [9] | REINA P, AHN S. On Macroscopic Freeway Merge Behavior: Estimation of Merge Ratios Using Asymmetric Lane Flow Distribution[J]. Transportation Research Part C: Emerging Technologies, 2015, 60: 24-35 |
| [10] | 高超. 北京市主次干道基本路段速度-流量关系模型研究[D]. 北京: 北京工业大学, 2008. GAO Chao. Research on Speed-flow Relationship Model of Beijing Primary and Secondary Roads Basic Roads [D]. Beijing: Beijing University of Technology, 2008. |
| [11] | Highway Capacity Manual. Transportation Research Board[M]. Washington, D.C.: National Research Council, 2000. |
| [12] | 詹琳霞. 城市快速路出入口设置影响因素研究[D]. 北京: 北京交通大学, 2008. ZHAN Lin-xia. Study on Influencing Factors of Establishment of Exits and Entrances of Urban Expressway[D]. Beijing: Beijing Jiaotong University, 2008. |
| [13] | 关羽, 张宁. 可变临界间隙条件下的加速车道车辆汇入模型[J]. 公路交通科技, 2010, 27(6): 117-120 GUAN Yu, ZHANG Ning. Vehicle Merging Model for Acceleration Lane under Condition of Changeable Critical Headway[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 117-120 |
| [14] | AHAMMED M A, HASSAN Y, SAYED T A. Modeling Driver Behavior and Safety on Freeway Merging Areas[J]. Journal of Transportation Engineering, 2014, 134(9): 370-377 |
| [15] | KONDYLI A, ELEFTERIADOU L. Modeling Driver Behavior at Freeway-ramp Merges[J]. Transportation Research Record, 2011, 2249: 29-37 |
| [16] | SARVI M, KUWAHARA M. Using ITS to Improve the Capacity of Freeway Merging Sections by Transferring Freight Vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 9(4): 580-588 |
| [17] | SARVI M, KUWAHARA M, CEDER A. Freeway Ramp Merging Phenomena in Congested Traffic Using Simulation Combined with a Driving Simulator[J]. Computer-Aided Civil and Infrastructure Engineering, 2004, 19(5): 351-363 |
| [18] | 王东柱, 陈艳艳, 马建明, 等. 车联网环境下的高速公路合流区协调控制方法及效果评价[J]. 公路交通科技, 2016, 33(9): 99-105 WANG Dong-zhu, CHEN Yan-yan, MA Jian-ming, et al. A Method for Coordinated Controlling Vehicles in Expressway Merge Area in Connected Vehicles Environment and Evaluation[J]. Journal of Highway and Transportation Research and Development, 2016, 33(9): 99-105 |
 2017, Vol. 34
2017, Vol. 34
