扩展功能
文章信息
- 张军伟, 谭阳, 陈拓, 申明德, 梅志荣
- ZHANG Jun-wei, TAN Yang, CHEN Tuo, SHEN Ming-de, MEI Zhi-rong
- 岩溶隧道侧部岩盘突水机制研究
- Study on Mechanism of Batholite Water Inrush in Lateral Karst Tunnel
- 公路交通科技, 2017, 34(5): 109-115
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(5): 109-115
- 10.3969/j.issn.1002-0268.2017.05.015
-
文章历史
- 收稿日期: 2016-05-30
2. 中国矿业大学 深部岩土力学与地下工程国家重点实验室, 江苏 徐州 221116;
3. 西南石油大学 土木工程与建筑学院, 四川 成都 610500;
4. 中铁西南科学研究院有限公司, 四川 成都 610031
2. State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining & Technology; Xuzhou Jiangsu 221116, China;
3. School of Civil Engineering and Architecture, Southwest Petroleum University, Chengdu Sichuan 610500, China;
4. China Railway Southwest Research Institute, Chengdu Sichuan 610031, China
为推动西部经济建设快速发展,国家加大了对其交通基础设施的建设投资。然而,由于我国岩溶面积高达3.443×106 km2,约占我国国土面积的1/3,其中以西南地区尤甚[1-3]。因此,在西南岩溶地区修建铁路、公路、水利、水封油库以及深部矿产等地下工程时将经常遭遇突水、岩爆、塌方、瓦斯、涌泥等大型地质灾害[2-4],其中以岩溶突水灾害最为严重。如何避免和处理岩溶突水问题,成为西部岩溶地区地下工程建设的关键。
近年来,国内外有关岩溶隧道突水突泥研究丰富,主要集中在下面两个方面:(1) 主要集中在工程地质与水文地质研究方面,比如岩溶的突水特征、岩溶赋存类型、涌突水的成因及岩溶水动态演变特征的研究,岩溶蓄水构造与岩溶涌(突)水的模式,岩溶隧道涌水量的预测方法、岩溶发育特征及涌水条件,岩溶管道-裂隙-孔隙三重孔隙介质地下水流模型及模拟方法等[1, 5-10];(2) 主要集中在隧道突水突泥的力学机制研究方面,比如深埋隧道突水突泥的力学机制分析,水-岩相互作用对岩溶地区隧道施工发生涌水、突泥的影响,导水裂隙扩展破坏的力学过程,施工中隧道岩盘安全厚度的确定方法等[1, 3, 4, 11-12]。上述研究多数只对隧道-岩溶系统来分类、抽象和概化,建立一系列如弹性梁板模型、岩墙模型等有代表性的典型力学模型[1, 4, 8, 11]。而这些力学模型研究的对象也仅限于完整围岩,并不适用于岩溶隧道断层段围岩。岩溶隧道断层段岩盘力学破坏机制的相关研究现已引起了地下工程研究领域的高度关注。大量实践表明,相当一部分比例的地下工程突水事故灾害与断层相关,据不完全统计,我国大型突水事故与断层相关的占50%以上,在煤矿突水中就有75%的突水与断层的形成机制有关[9, 13]。然而,对于岩溶隧道断层段岩盘力学破坏机制的理论研究鲜有报道。因此,开展岩溶隧道断层段岩盘力学破坏机制研究对保证岩溶区隧道的安全性、经济性具有直接的推动作用。
以下研究对隧道-岩溶系统进行抽象概化,建立了溶腔位于隧道侧面条件下溶腔张性断层突水力学模型,并将断层的形成机理引入到溶腔压性断层突水力学模型,推导了岩溶隧道压性断层段岩盘最小安全厚度计算公式,为更加合理确定岩溶隧道断层段的岩盘安全厚度提供了有效的计算方法,对工程实际具有科学指导意义。
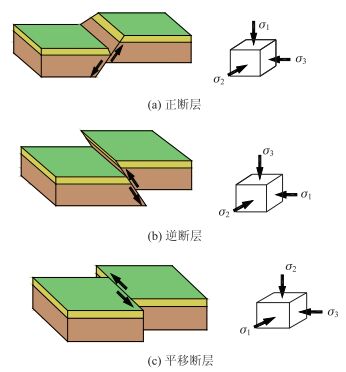
1 断层形成机理及突水模式 1.1 断层形成机理岩石破裂的临界状态发生在其受力超过强度,即应力差大于等于强度时。起初,岩石出现微裂隙,由微裂隙延伸、发展、联合形成破裂面,将岩石分裂为两盘。一旦应力差逐渐增大至超过两盘间的摩擦阻力,两盘相对运动产生断层[14]。依据上述断层形成原理,E.M.Anderson等[15]提出如图 1所示3种不同应力状态下的断层类别。
|
| 图 1 断层形成机理 Fig. 1 Fault formation mechanism |
| |
如图 1(a)所示,形成正断层的应力状态是最大主应力σ1垂直、σ2和σ3水平;σ2与断层走向一致,上盘顺断层倾斜向下滑动,这样的力学机理决定了正断层属于张开型断层。形成逆断层的应力状态是最大主应力轴σ1和中间主应力轴σ2是水平的,最小主应力轴σ3是垂直的,σ2平行于断层面走向,水平挤压力越大越利于逆断层的形成,继而可知逆断层属于压性断层,如图 1(b)所示。图 1(c)为形成平移断层的应力状态,它的最大主应力轴σ1和最小主应力轴σ3是水平的,中间主应力轴σ2是垂直的。断层面走向与滑动面方向都垂直于σ2,属于扭性断层。除了张性、压性和扭性断层外还存在着压扭性断层,如表 1所示的平移逆断层或者逆平移断层。
| 断层类型 | 分类 | |
| 压性断层 | 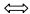 | 逆断层(包括冲断层、逆掩断层) |
| 张性断层 | 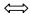 | 正断层 |
| 扭性断层 | 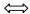 | 平移断层 |
| 压扭性断层 | 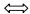 | 平移逆断层、逆平移断层 |
1.2 断层引发的突水模式
隧道开挖穿越断层的方式有3种[13],分别为隧道走向与断层走向一致,隧道走向与断层走向垂直,隧道走向与断层走向斜交。不同的穿越方式所引发的突水机理各有不同。以下内容只讨论隧道走向与断层走向一致情况下岩溶隧道突水的力学机理。一般认为断层引发突水的模式有:
(1) 在高压水作用下断层两盘关键层产生强度破坏导致突水。
(2) 断层带处岩体破碎或者两盘间隙过大,导水性好,导致突水。
(3) 断层活化(或重新张开时),承压水在断层带内渗透流动冲刷形成导水通道,导致突水。
2 力学模型 2.1 假设条件如果将断层引发突水简化为相似的力学模型来分析,则主要讨论岩体关键层产生强度破坏所造成的突水。郭佳奇[16-17]认为针对大尺度溶腔与隧道间岩层可简化为弹性梁板进行分析。前提是进行以下假设:
(1) 溶腔规模相对于隧道尺寸较大。溶腔位于隧道侧部时,隧道横断面内溶腔垂直隧道轴线方向的尺寸为隧道高度的两倍以上;溶腔分别位于隧道顶、底板时,水平面内溶腔垂直隧道轴线方向的尺寸为隧道跨度的两倍以上。不考虑隧道与溶腔间岩盘的成拱效应。
(2) 将溶腔对隧道的威胁抽象为溶腔内部均布的岩溶水压力和岩溶沉积物的荷载之和,针对溶腔分布的不同位置作相应突水类型的力学分析。
(3) 隧道与溶腔间岩盘为连续均匀的各向同性弹性体,符合小变形理论,能同时承受拉应力和压应力。
实际上由于断层对岩盘岩层的作用,为了简化计算,以下根据实际情形考虑将岩盘岩层受力模型简化为两端固梁支力学模型。
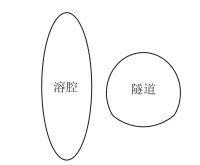
2.2 岩盘厚度的力学模型当溶腔分布于隧道的侧面时,溶腔主要受到溶腔内水压力以及溶腔充填物压力作用,压性断层结构力学模型可将图 2中溶腔与隧道之间的岩盘简化为图 3所示的固支梁结构,并按此结构计算梁的内力。
|
| 图 2 溶腔分布于隧道侧面 Fig. 2 Cavity distributing in side of tunnel |
| |
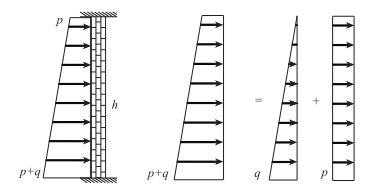
|
| 图 3 侧方溶腔压性断层突水力学模型 Fig. 3 Water bursting mechanical model of lateral cavity in compressional fault |
| |
最大剪力
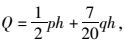
|
(1) |
最大弯矩
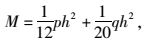
|
(2) |
式中,p为溶腔内与隧道拱顶等高处水压力;h为防突岩层高度;q为溶腔内充填物沿垂直方向压力。

|
式中, ρ为溶腔内充填物密度;g为重力加速度。
按抗弯强度公式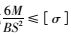
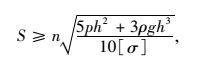
|
(3) |
式中,B为梁的宽度,取1 m;S为梁的厚度,即岩盘厚度;[σ]为岩体许用抗弯强度;修正系数n取0~1。
按抗剪强度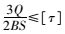
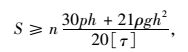
|
(4) |
式中[τ]为岩体许用抗剪强度。
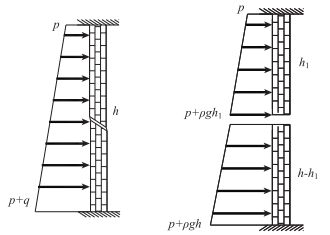
考虑到张性断层的影响,此时将如图 3所示岩盘岩层的力学结构模型简化为如图 4所示的上下受力不同的结构。
|
| 图 4 侧方溶腔张性断层突水力学模型 Fig. 4 Water bursting mechanical model of lateral cavity in tensional fault |
| |
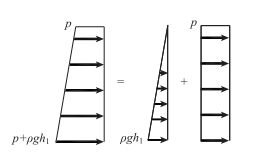
对于图 4中右部的上部结构,对其进行力学分析,将梯形荷载简化为图 5所示的三角形荷载和矩形荷载。
|
| 图 5 岩盘上部结构突水力学模型 Fig. 5 Water bursting mechanical model of top structure of batholite |
| |
最大剪力
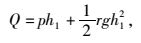
|
(5) |
最大弯矩
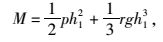
|
(6) |
式中h1为岩盘岩层上部高度。
按抗弯强度公式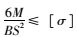
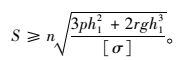
|
(7) |
按抗剪强度公式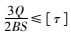
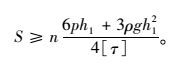
|
(8) |
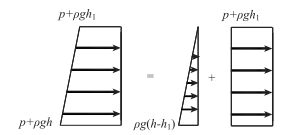
对于图 4中右部的下部结构,对其进行力学分析,将梯形荷载简化为图 6所示的三角形荷载和矩形荷载。
|
| 图 6 岩盘下部结构突水力学模型 Fig. 6 Water bursting mechanical model of bottom structure of batholite |
| |
最大剪力
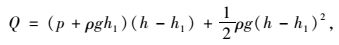
|
(9) |
最大弯矩
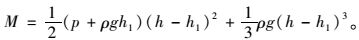
|
(10) |
按抗弯强度公式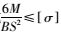
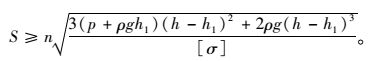
|
(11) |
按抗剪强度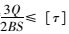
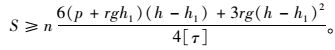
|
(12) |
通过以上理论分析得出了溶腔分布于隧道侧面时含压性断层与含张性断层时,简化防突岩层厚度的相关力学公式,取岩体的抗压强度80 MPa,抗弯强度为抗压强度的0.15倍,抗剪强度为抗压强度的0.09倍,岩体重度为24.5 kN/m3,隧道跨度为15 m,水压力从0 MPa变化到3 MPa时,可得到水压力与相应防突层厚度关系曲线。
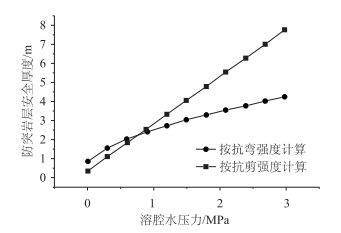
对于压性断层,将岩体岩盘岩层简化为两端固支的梁,按抗弯以及抗剪公式得出的水压力与安全厚度曲线如图 7所示。
|
| 图 7 压性断层情况水压力及安全厚度曲线 Fig. 7 Curves of water pressure and safe thickness of tensional fault |
| |
由曲线可知,按抗弯及抗剪强度计算得出的岩层安全厚度都随着水压力的增大而不断增大,但是水压力较小时按抗弯强度进行计算的安全厚度较大,即水压力在0~0.8 MPa之间时按抗弯强度计算安全厚度,水压力在大于0.8 MPa时应按抗剪强度来计算岩层的安全厚度。
对于张性断层,由于断层作用于防突岩层,将其分为上下两部分,根据结构力学原理分别推导出上下部分岩体的安全厚度理论公式,并进行修正。此时假设岩体的抗拉强度为12 MPa,抗剪强度为7.2 MPa,当隧道上侧部高度h1为5 m时,下侧部岩体高为10 m,代入以上数据可得水压力从0 MPa变化到3 MPa时安全厚度的变化值。
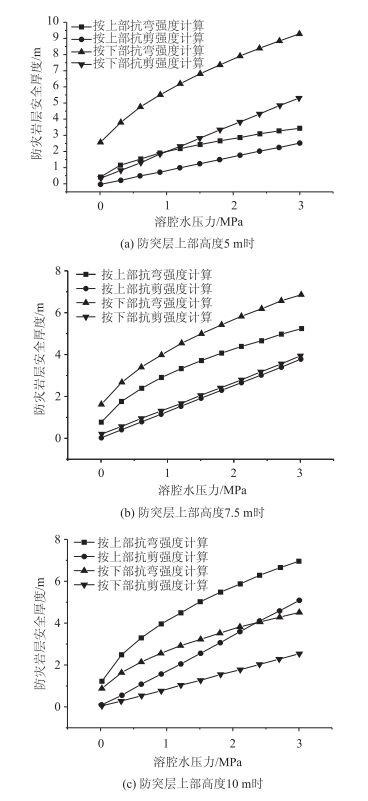
由图 8(a)可知按下部抗弯强度计算所得曲线的数值明显大于其他3条线的值,即侧部岩体下部结构断层处最易造成突水,因此岩体的安全厚度最大,在计算防突层的安全厚度时应采用侧方下部结构抗弯公式推导出的安全厚度值进行验算。当隧道侧部上下部分岩体高度一致时,即均为7.5 m时也可以得出相应的曲线,见图 8(b)。
|
| 图 8 张性断层情况水压力及安全厚度曲线 Fig. 8 Curves of water pressure and safe thickness of tensional fault |
| |
由图 8(b)可知岩盘安全厚度仍应按侧方下部岩体的抗弯计算公式计算,当断层分布于隧道侧部岩体中部,溶腔水压力达到3 MPa时,最大安全厚度接近7 m;上下部岩体按抗剪强度得出的安全厚度结果基本一致。当侧方上部岩体高为10 m时,可得图 8(c)。
由图 8(c)知,随着溶腔水压力的增大,侧方上部结构按抗弯强度得出的岩层安全厚度最大,说明其最易产生破坏;当水压力达到3 MPa时,最大安全厚度基本达到7 m,为保障隧道安全,此时应该用侧方上部岩体的抗弯安全厚度计算。并且侧方上部分岩体不管是按抗剪计算还是抗弯强度计算的安全厚度值都大于下部分,说明上部分更容易造成破坏,此结果与图 10的结果相互对应。
3 算例分析大支坪隧道位于宜万铁路线恩施土家族苗族自治州巴东县大支坪镇,为单线铁路隧道,其中,Ⅰ线全长8 775 m,Ⅱ线全长8 789 m,隧道最大埋深495 m,隧道纵坡为人字坡,进口段Ⅱ线右侧30 m设置有长3 991 m的排水洞。隧道沿线不良地质分布主要有岩溶、瓦斯、断层破碎带等。在唐坪向斜核部、栖霞组底部、长兴组、大冶组底部以及断层附近均为岩溶集中发育和岩溶水富集地段,此段极可能发生隧道内突水、突泥等岩溶灾害。Ⅰ线DKl32+947~DKl32+957和DK133+006~DK133+027段、Ⅱ线IIDK132+913~IIDK132+921和DKl32+973~DKl32+997段分布有大型富水充填溶洞,简称“990溶腔”[18]。以上大型富水充填溶洞基本上沿层面及岩层走向发育,Ⅰ、Ⅱ线隧道溶洞连通,尖灭于排水洞左边墙。其中,Ⅰ线左侧(以至万县方向为基准方向)DKl32+960~DKl32+980段有大型富水充填溶腔发育,溶腔充填物主要为砂夹卵砾石。“990溶腔”段隧道最大埋深495 m,基本为Ⅱ级围岩,溶腔与地表岩溶洼地通过不良地质段内的岩溶管道和裂隙相通,地下水受大气降水控制,补给条件良好。但是,由于该溶洞被砂夹卵砾石充填,观测到的水压力为溶腔充填物的渗透水压力,最大水压0.24 MPa。
溶腔分布于隧道左侧,充填物密度为24.5 kN/m3,溶腔跨度15 m,高8 m,岩石单轴抗压强度为10.5 MPa,抗拉强度为1.0 MPa。岩体许用抗剪强度取为0.09倍的岩石抗压强度,即0.945 MPa。
当岩盘厚度为完整岩体时取式(3) 进行验算:
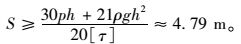
|
当岩盘厚度为非完整岩体时:取h1=0,得出极限安全厚度值,取公式(11) 进行验算:
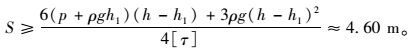
|
DK132+960~DK132+980段富水充填溶腔距离大支坪隧道Ⅰ线左侧(以万县方向为基准方向)边墙距离为3~5 m,由上述计算的岩盘安全厚度知,在该段隧道施工时,极有可能发生突水、突泥等岩溶灾害。隧道施工过程中根据岩溶发育情况和水文地质条件,综合考虑施工及运营安全等多种因素,遵循“排水降压、注浆加固、超前支护、综合治理”的原则进行综合处理,最终顺利通过了该侧部富水充填溶腔影响段。
4 结论本文围绕岩溶隧道断层段岩盘力学破坏机制,建立了溶腔位于隧道侧面条件下的断层突水力学模型,并推导了岩溶隧道断层段岩盘最小安全厚度计算公式,结合工程实例就岩盘最小安全厚度的确定进行了讨论,获得如下结论:
(1) 对于压性断层(或是完整的岩盘),受侧向溶腔作用时,根据抗剪强度得到的最小安全厚度比根据抗弯强度更敏感。出于安全考虑,当水压小于0.8 MPa时,最小安全厚度值应按照抗弯强度分析,大于0.8 MPa时,情况相反;当水压为0 MPa时,由于仍受溶腔填充物压力作用或是岩层自重的原因,岩盘厚度不能为零。
(2) 对于张性断层,侧方岩体上下等长时,下方更易被破坏;不等高时,较长的部分更易被破坏。出于安全考虑,应根据实际情况选择下部岩体或较长部岩体根据抗弯强度计算最小安全厚度。
(3) 岩溶隧道断层段岩盘最小安全厚度受隧道岩盘力学性质、溶腔水压以及隧道半径的影响。岩盘抗剪强度越大(岩盘较硬),最小安全厚度越小,突水不易发生;半径越大,最小安全厚度越大,即一次开挖暴露面较大时,突水更易发生。
(4) 通过宜万线大支坪隧道实例分析,在岩溶隧道断层段施工过程中,为保证施工安全,防止灾害发生,应广泛考虑各项易致灾因素,在安全厚度确定后,采取含水层释能降压,开挖面预注浆,小断面分布弱爆破开挖等手段谨慎通过。
| [1] | 孙谋, 刘维宁. 高风险岩溶隧道掌子面突水机制研究[J]. 岩土力学, 2011, 32(4): 1175-1180 SUN Mou, LIU Wei-ning. Research on Water Inrush Mechanism Induced by Karst Tunnel Face with High Risk[J]. Rock and Soil Mechanics, 2011, 32(4): 1175-1180 |
| [2] | 李术才, 林鹏, 许振浩, 等. 基于条分法原理的充填型岩溶蓄水构造突水突泥最小安全厚度[J]. 岩土力学, 2015, 36(7): 1989-1994 LI Shu-cai, LIN Peng, XU Zhen-hao, et al. Minimum Safety Thickness of Water and Mud Inrush Induced by Filled-type Karst Water Bearing Structures Based on Theory of Slice Method[J]. Rock and Soil Mechanics, 2015, 36(7): 1989-1994 |
| [3] | 臧守杰. 强岩溶区隧道施工中隧底最小安全厚度分析研究[J]. 隧道建设, 2007, 27(5): 17-19 ZANG Shou-jie. Theoretical Study on Minimum Safe Thickness of Floors of Tunnels in Heavy Karst Areas during Construction[J]. Tunnel Construction, 2007, 27(5): 17-19 |
| [4] | 李利平, 路为, 李术才, 等. 地下工程突水机理及其研究最新进展[J]. 山东大学学报:工学版, 2010, 40(3): 104-112 LI Li-ping, LU Wei, LI Shu-cai, et al. Research Status and Developing Trend Analysis of the Water Inrush Mechanism for Underground Engineering Construction[J]. Journal of Shandong University: Engineering Science Edition, 2010, 40(3): 104-112 |
| [5] | 刘招伟, 何满潮, 王树仁. 圆梁山隧道岩溶突水机理及防治对策研究[J]. 岩土力学, 2006, 27(2): 228-232 LIU Zhao-wei, HE Man-chao, WANG Shu-ren. Study on Karst Waterburst Mechanism and Prevention Countermeasures in Yuanliangshan Tunnel[J]. Rock and Soil Mechanics, 2006, 27(2): 228-232 |
| [6] | 臧守杰, 綦彦波, 程建铝. 喀斯特地区隧道施工中隧底岩层稳定性评价研究[J]. 水利与建筑工程学报, 2007, 5(3): 43-45 ZANG Shou-jie, QI Yan-bo, CHENG Jian-lü. Evaluation and Research on Stability of Bottom Rock Layer in Construction of Tunnel in Karst Area[J]. Journal of Water Resources and Architectural Engineering, 2007, 5(3): 43-45 |
| [7] | 邬立, 万军伟, 陈刚, 等. 宜万铁路野三关隧道"8.5"突水事故成因分析[J]. 中国岩溶, 2009, 28(2): 212-218 WU Li, WAN Jun-wei, CHEN Gang, et al. Cause of the "8.5" Water Burst Incident at Yesanguan Tunnel along the Yi-Wan Railway[J]. Carsologica Sinica, 2009, 28(2): 212-218 |
| [8] | 周宗青, 李术才, 李利平, 等. 岩溶隧道突涌水危险性评价的属性识别模型及其工程应用[J]. 岩土力学, 2013, 34(3): 818-829 ZHOU Zong-qing, LI Shu-cai, LI Li-ping, et al. Attribute Recognition Model of Fatalness Assessment of Water Inrush in Karst Tunnels and Its Application[J]. Rock and Soil Mechanics, 2013, 34(3): 818-829 |
| [9] | ZHANG Jun-wei, LI Lei, MA Xiao-jie, et al. Waterproofing of a Bored Tunnel by Employing an Innovation Composite Membrane[J]. Electronic Journal of Geotechnical Engineering, 2014, 19: 2565-2577 |
| [10] | 刘学利, 汪彦. 塔河缝洞型油藏溶洞相多点统计学建模方法[J]. 西南石油大学学报:自然科学版, 2012, 34(6): 53-58 LIU Xue-li, WANG Yan. Multi-point Geostatistical Multi-point Geostatistical Approach to Model Karst Facies of Fracture-cavity Reservoir in Tahe Oilfield[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2012, 34(6): 53-58 |
| [11] | 李青锋, 王卫军, 朱川曲, 等. 基于隔水关键层原理的断层突水机理分析[J]. 采矿与安全工程学报, 2009, 26(1): 87-90 LI Qing-feng, WANG Wei-jun, ZHU Chuan-qu, et al. Analysis of Fault Water-Inrush Mechanism Based on the Principle of Water-resistant Key Strata[J]. Journal of Mining & Safety Engineering, 2009, 26(1): 87-90 |
| [12] | 李宗杰, 刘群, 李海英, 等. 地震古岩溶学理论及应用[J]. 西南石油大学学报:自然科学版, 2013, 35(6): 9-19 LI Zong-jie, LIU Qun, LI Hai-ying, et al. Theory and Application of Seismic Palaeokarst[J]. Journal of Southwest Petroleum University: Science & Technology Edition, 2013, 35(6): 9-19 |
| [13] | 罗雄文, 何发亮. 深长隧道突水致灾构造及其突水模式研究[J]. 现代隧道技术, 2014, 51(1): 21-25 LUO Xiong-wen, He Fa-liang. A Study of Geological Structures Inclined to Disaster and Models of Water Burst in Deep-buried Long Tunnels[J]. Modern Tunneling Technology, 2014, 51(1): 21-25 |
| [14] | 雷光伟, 杨春和, 王贵宾, 等. 断层影响带的发育规律及其力学成因[J]. 岩石力学与工程学报, 2016, 35(2): 231-241 LEI Guang-wei, YANG Chun-he, WANG Gui-bin, et al. The Development Law and Mechanical Causes of Fault Influenced Zone[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(2): 231-241 |
| [15] | FITZPATRICK M L. Facsimile Reproduction of the Dynamics of Faulting by E. M. Anderson[J]. Developmental Dynamics, 2005, 234(3): 756-766 |
| [16] | 郭佳奇. 岩溶隧道防突厚度及突水机制研究[D]. 北京: 北京交通大学, 2011. GUO Jia-qi. Study on Against-inrush Thickness and Waterburst Mechanism of Karst Tunnel[D]. Beijing:Beijing Jiaotong University, 2011. |
| [17] | 郭佳奇, 乔春生. 岩溶隧道掌子面突水机制及岩墙安全厚度研究[J]. 铁道学报, 2012, 34(3): 105-111 GUO Jia-qi, QIAO Chun-sheng. Study on Water-inrush Mechanism and Safe Thickness of Rock Wall of Karst Tunnel Face[J]. Journal of the China Railway Society, 2012, 34(3): 105-111 |
| [18] | 马栋. 深埋岩溶对隧道安全影响分析及处治技术研究[D]. 北京: 北京交通大学, 2012. MA Dong. Study on Impact Mechanism of Deep Buried Karst to Tunnel Safety and Treatment Technique[D]. Beijing:Beijing Jiaotong University, 2012. |
 2017, Vol. 34
2017, Vol. 34
