扩展功能
文章信息
- 鲁圣弟, 熊文, 丁旭东, 叶见曙, 韦国志
- LU Sheng-di, XIONG Wen, DING Xu-dong, YE Jian-shu, WEI Guo-zhi
- 桥型布置对独柱墩曲线梁桥抗倾覆性能的影响
- Influence of Structure Arrangement on Anti-overturn Performance of Curved Beam Bridge with Single-column Piers
- 公路交通科技, 2017, 34(5): 95-101
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(5): 95-101
- 10.3969/j.issn.1002-0268.2017.05.013
-
文章历史
- 收稿日期: 2016-05-19
2. 东南大学 交通学院, 江苏 南京 210096
2. School of Transportation, Southeast University, Nanjing Jiangsu 210096, China
中小跨径独柱墩曲线梁桥既可适应桥梁所处环境对桥型布置的要求,也能改善交通枢纽的外观;同时还有效减少占用土地,避免桥梁基础与地下建筑位置之间的冲突,并节省工程材料。相比双柱桥墩结构,其简洁的下部结构布置形式亦可减少对自然环境的破坏[1]。特别对于梁底宽度较窄的匝道桥,独柱墩结构显然是其优选的布置形式。但在车辆偏载作用下,其单支点的支承形式对桥梁结构整体抗倾覆稳定性十分不利[2-3]。事实上我国近年来发生过数起独柱墩梁桥整体倾覆事件,造成的危害极大,带来严重的经济损失和社会负面效应,所以必须在设计阶段确保该类桥梁在运营过程中具备足够合理的抗倾覆安全储备。
我国规范已采用抗倾覆稳定安全系数这一概念描述其安全性,并对独柱墩梁桥的抗倾覆分析给出了相关条文。例如:《公路钢筋混凝土及预应力混凝土桥涵设计规范(征求意见稿)》(JTG D62—2012) 给出整体式断面中小跨径桥上部结构抗倾覆稳定性系数的分析过程,并规定不应小于2.5[4];《铁路桥涵设计基本规范》(TB10002.1—2005) 规定梁式桥跨结构在计算荷载最不利组合作用下,横向倾覆稳定系数不应小于1.3,并给出了具体的验算方法[5]。但是现行规范中并不区分分析对象梁的不同桥型布置形式,即无论采用曲线梁还是直线梁,或者采用不同的曲率半径与不同的跨径布置,均基于同一分析方法与模式去计算抗倾覆稳定安全系数,并简单地与一下限数值进行比较以判断结构抗倾覆的安全性。显然现行规范所提供的分析方法过于简单与单一,无法针对不同桥型布置的独柱墩曲线梁桥进行准确的抗倾覆安全性分析。
为研究这一问题,文中以3×30 m的独柱墩混凝土曲线梁桥作为基本结构,建立不同桥型布置形式的独柱墩桥有限元模型,利用非线性及接触理论精细化考察倾覆过程中结构位移、转角以及支座反力的时程变化规律。进而计算抗倾覆稳定安全系数,分析不同桥型布置下独柱墩曲线梁桥抗倾覆能力及力学特征,得出桥型布置关键设计参数对独柱墩倾覆力学行为的影响。同时将规范法计算结果与有限元法计算结果进行对比,考察规范法验算不同桥型布置的独柱墩曲线梁桥抗倾覆稳定性的准确性与适用性,为该类新桥设计建设及旧桥改造加固提供分析依据,为相关规范条文的进一步修订建立理论基础。
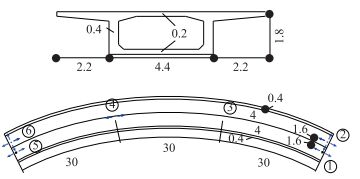
1 分析结构描述 1.1 基本结构选择曲线跨径3×30 m、曲线半径100 m的独柱墩混凝土曲线连续箱梁桥作为文中研究的基本研究对象。桥梁截面及平面布置见图 1,桥面全宽8.8 m,行车道宽度为8 m,曲线梁半径为100 m。
|
| 图 1 结构截面与平面布置形式(单位:m) Fig. 1 Layouts of structural cross-section and plane(unit: m) |
| |
图 1中桥台采用双支座抗扭支承,两支座横向间距3.2 m,沿结构中线对称布置,中墩为单支点设置且无偏心,桥台为GPZ2型号盆式支座,中墩为GPZ10型盆式支座。将支座沿圆弧外侧行车方向依次编号为①~⑥,图中箭头表示活动支座可以移动的方向,设计参数见表 1。
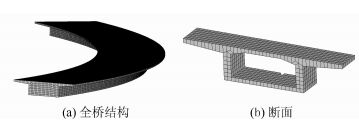
利用大型有限元程序ANSYS对该基本结构进行精细化有限元建模。混凝土采用三维实体单元solid65模拟,混凝土强度等级C40;支座橡胶采用三维实体单元solid185模拟。利用面面接触单元(Targe170、Conta174) 模拟主梁底面与支座面之间的接触行为;支座体竖向划分为4层单元,中墩支座每层再划分为128个单元(径向×切向=8×16),边墩支座每层再划分为96个单元(径向×切向=8×12),所有单元均近似为矩形,形状较为规则。通过计算结果,能准确计算模拟出支座受偏压、局部脱空、局部变形等倾覆过程中的支座典型力学行为。《公路钢筋混凝土及预应力混凝土桥涵设计规范(征求意见稿)》(JTG D62—2012)(下文中简称规范)中对抗倾覆稳定性的要求为:公路-Ⅰ级车道荷载所验算得到的上部结构抗倾覆安全系数不小于2.5。为与规范保持一致性,此处亦采用公路-Ⅰ级荷载进行偏载加载。有限元模型见图 2。
|
| 图 2 有限元模型 Fig. 2 Finite element model |
| |
按规范给出的最不利倾覆轴判断方法与原则,通过计算可知:当曲线梁曲线半径大于550 m时,倾覆轴线为边墩外侧支座连线。当曲线半径小于550 m时,对于本文中给定的桥型,见图 1,中墩支座在边墩支座连线外侧,最不利倾覆轴线为两中墩支座连线,此时稳定力矩最小。加载时,公路-Ⅰ级荷载加载范围为倾覆轴线的外侧,同时按规范给出的车辆横向布置最小距离来定荷载的最不利偏载位置,具体可见规范相关条文与附图。
加载分两步进行,第1个时间步加载重力荷载;第2个时间步加载公路-Ⅰ级荷载,按最不利偏载布置(偏向曲线外侧),并不断按倍数增大荷载直至计算发散,此时认为结构发生整体倾覆倒塌,结构功能完全失效。计入几何、材料双重非线性并考虑接触分析,跟踪结构倾覆全过程的力学行为变化[8-13]。
1.2 参数分析对象为研究桥型布置对独柱墩曲线梁桥抗倾覆性能的影响,以图 1与图 2给出的结构为基础,改变曲线梁半径形成以下10种不同的桥型布置以进行参数分析。
同时,为研究边中跨比对独柱墩曲线梁桥抗倾覆性能的影响,仍以图 1与图 2为基础,桥梁三跨全长90 m不变,曲线梁半径选为500 m,建立边中跨比为1.00,0.90,0.80,0.70(中跨长分别为30,32.2,34.6,37.5 m)的4种桥型布置进行参数分析。
由于橡胶支座本身刚度远小于桥墩刚度,桥墩刚度在整个倾覆过程及倾覆诱因中并不占主导地位,而计算模型已详细计入支座的物理性能与力学行为,故本文并未对桥墩刚度进行单独的参数分析。
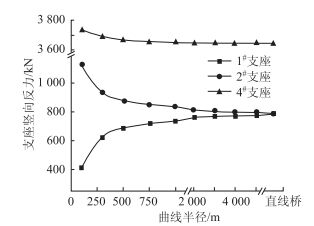
2 曲线梁半径参数分析结果 2.1 支座反力与整体转角按第1节给出的结构尺寸与精细化建模方法,首先给出表 2中不同曲线梁半径桥型布置下恒载作用时各支座反力的计算结果,见图 3。
| 编号 | 单跨弧 长/m | 跨数 | 弧长/ m | 曲线半 径/m | 圆心角/ (°) | 单跨圆 心角/(°) |
| 1 | 30 | 3 | 90 | 100 | 51.566 2 | 17.188 7 |
| 2 | 30 | 3 | 90 | 300 | 17.188 7 | 5.729 6 |
| 3 | 30 | 3 | 90 | 500 | 10.313 2 | 3.437 7 |
| 4 | 30 | 3 | 90 | 750 | 6.875 4 | 2.291 8 |
| 5 | 30 | 3 | 90 | 1 000 | 5.156 6 | 1.718 9 |
| 6 | 30 | 3 | 90 | 2 000 | 2.578 3 | 0.859 4 |
| 7 | 30 | 3 | 90 | 3 000 | 1.718 9 | 0.573 0 |
| 8 | 30 | 3 | 90 | 4 000 | 1.289 2 | 0.429 7 |
| 9 | 30 | 3 | 90 | 5 000 | 1.031 3 | 0.343 8 |
| 10 | 30 | 3 | 90 | 直线桥 | — | — |
|
| 图 3 恒载作用下支座反力 Fig. 3 Supporting forces under dead load |
| |
图 3可见,随曲线半径增大,边墩外侧支座(图 1中② 号支座)竖向反力逐渐减小,边墩内侧支座(图 1中① 号支座)竖向反力逐渐增加,当按直线桥布置时,两者数值一致。也就是说,改变独柱墩桥的曲线半径,对两侧双支座反力影响较大,中间独柱墩单点支座(图 1中④ 号支座)反力几乎不受影响。这主要是因为曲线梁桥内外侧弧长不一致,在整体扭矩作用下,会使外梁超载,内梁卸载,曲线半径越小,内外侧支座反力相差越大[14-15]。对于小半径的曲线梁桥,在恒载作用下应注意控制内侧支座反力,必要时可优化下部结构或支座形式,减小内侧支座出现脱空的可能性。
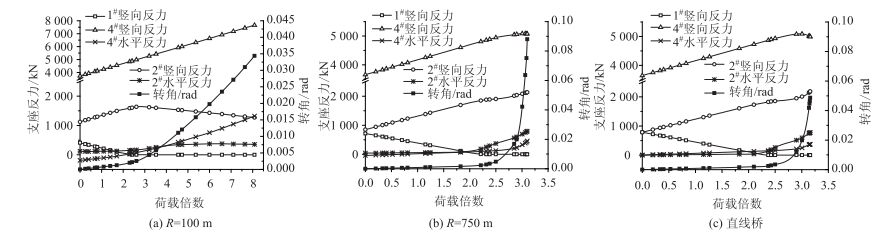
进而按公路-Ⅰ级荷载进行偏载加载(偏向曲线外侧)的极限状态分析。加载过程结构外侧偏转,内侧支座不断卸载,支座发生脱空现象, 见图 4。脱空后桥梁支承点减少,外侧支座竖向反力增大,变形以上部结构整体转动为主,随荷载不断增大,计算最终发散,结构不稳定而整体倾覆。图 5给出不同曲线半径下结构加载至发散全过程边墩内、外侧支座及中墩支座的反力变化图(限于篇幅仅给出100,750 m及直线桥的计算结果,如左侧纵坐标所示),并给出主梁整体转角变化图(右侧纵坐标所示,利用两腹板与底板相交位置的相对高差除以底板宽度得到)。横坐标为所加载荷载相对于公路-Ⅰ级的倍数关系,倍数越大加载荷载越大。

|
| 图 4 支座脱空 Fig. 4 Disengagement of bearing |
| |
|
| 图 5 支座反力与转角变化曲线 Fig. 5 Curves of supporting force and rotation |
| |
图 5可以看出,在偏载作用下,桥梁转角不断增大,偏载一侧支座(2#支座)竖向反力也随之增加。特别是转角一旦超过0.02 rad,其增幅迅速增大,桥梁随即进入不稳定的力学状态,倾覆几率大大提高。同时2#,4#支座水平反力急剧增加,对桥墩产生水平推力,此时若下部结构刚度不足,桥墩变形会明显加剧上部结构的整体失稳。
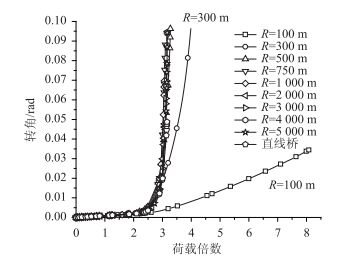
另外,图 5中无论何种曲线半径,随偏载不断增大,内侧支座(1#支座)反力均逐渐减小,直至进入脱空状态。一旦该内侧支座脱空,支座反力便重新分配,此时边墩外侧支座(2#支座)竖向反力增速减缓,而中墩单支座(4#支座)竖向反力仍持续增大,最终支座达到极限状态,发生塑性变形,从而导致主梁整体侧向转角急剧增加直至倾覆破坏。但是,对比图 5(a)、5(b)与5(c)又可明显看出,当偏载增大时,半径为100 m的曲线梁整体转角变化较为平缓,并未像半径750 m及直线桥一样出现在较小荷载增量下转角发生明显突变而倾覆失稳的现象。若将不同曲线半径独柱墩梁桥的整体转角随荷载变化的曲线绘至图 6中,又可进一步看出:曲线半径大于500 m的独柱墩梁其转角变化曲线基本呈相同趋势,外荷载超过一定值后,微小的增加都会使桥梁产生较大的整体转动,及支座脱空后更易进入不稳定状态。而对于半径小于500 m的独柱墩梁,虽然荷载较小时便发生支座脱空,但之后主梁转角变化相对平缓,在荷载持续增大过程中反而具有较好的空间稳定性。
|
| 图 6 转角变化曲线 Fig. 6 Curves of rotation |
| |
2.2 抗倾覆安全系数
此处定义独柱墩曲线梁桥倾覆全过程中,某一倾覆临界状态所施加荷载(仅包括偏载活载)相对于初始荷载公路-Ⅰ级的倍数为该验算荷载所对应的抗倾覆安全系数。抗倾覆安全系数越大,表明抗倾覆的安全性越好,安全储备越高;而抗倾覆安全系数越小,则安全储备低,更容易发生倾覆。根据有限元计算结果,文中所建立的不同曲线半径的独柱墩梁桥,支座脱空、整体转角达到0.02 rad以及计算发散结构倾覆这3种临界状态对应于公路-Ⅰ级车道荷载的安全系数分别列于表 3。为方便对比,将同样基于公路-Ⅰ级车道荷载而按规范方法进行计算的安全系数同时列于表 3。
| 半径/m | 支座脱空 | 整体转角= 0.02 rad | 倾覆 (计算发散) | 规范方法 |
| 100 | 2.05 | 5.13 | 6.87 | 6.53 |
| 300 | 1.84 | 2.56 | 3.63 | 2.51 |
| 500 | 1.86 | 2.45 | 2.78 | 1.97 |
| 750 | 1.87 | 2.46 | 2.63 | 2.56 |
| 1 000 | 1.92 | 2.47 | 2.60 | 3.94 |
| 2 000 | 1.97 | 2.51 | 2.61 | 6.62 |
| 3 000 | 1.97 | 2.52 | 2.66 | 7.90 |
| 4 000 | 1.98 | 2.53 | 2.67 | 8.64 |
| 5 000 | 1.99 | 2.53 | 2.69 | 9.12 |
| 直线桥 | 2.01 | 2.56 | 2.68 | 11.41 |
表 3可以看出,对于曲线半径小于750 m的独柱墩梁桥,除以支座脱空控制的临界状态之外,有限元与规范法计算的安全系数在数值与变化规律上均比较接近。而对于曲线半径大于750 m的梁,无论是支座脱空、整体转角达到0.02 rad还是计算发散结构倾覆临界状态,有限元法得出的安全系数均远小于规范方法。也就是说,在设计过程中,若按规范方法进行抗倾覆安全系数的计算,对于半径大于750 m的独柱墩曲线梁桥,会大大高估其抗倾覆的安全性能。且随曲线半径的增大,规范方法对安全性能的高估会愈加明显,特别针对直线独柱墩梁桥,安全系数高达11.41,远大于有限元计算结果。这主要因为曲线半径较小时,各支承点相对分散,支承面比较稳定;而当曲线半径较大时,支承点连线接近直线,显然承受偏载时更易失稳。所以,在设计中若直接采用规范法得到抗倾覆安全系数进行大半径独柱墩曲线梁桥的设计,往往会导致实际抗倾覆能力储备不足。这也是实际发生倾覆事故的独柱墩梁桥多为大曲线半径或直线梁桥的原因[16-18]。
另外,表 3中规范法明显高估独柱墩梁桥的抗倾覆能力,通过对比其主要原因为:(1) 规范法忽略结构自身的扭转变形,将其视为刚性体绕固定倾覆轴进行的简单转动问题;(2) 规范法不考虑倾覆后期的几何、材料非线性问题;(3) 规范法不考虑支座超弹性材料的变形影响,仅将支座理想化为点支承;(4) 规范法不考虑倾覆过程中的不同临界阶段。
综上,无论从支座反力、整体转角还是抗倾覆安全系数来看,对于曲线半径大于500 m的独柱墩梁桥,不能仅依靠现有规范方法来判定其抗倾覆安全性能与储备,必须结合精细化有限元分析结果进行结构设计,必要时应采取构造措施提高其抗倾覆性能,以保证运营阶段的安全性。
3 边中跨比参数分析结果 3.1 支座反力与整体转角半径为500 m的独柱墩曲线梁桥3种倾覆临界状态有限元方法得到的安全系数与规范方法得到安全系数相比均较小(表 3),即具有较小的抗倾覆安全储备。本节基于该曲线半径的精细化有限元模型,通过参数分析给出表 4中不同边中跨比桥型布置下恒载作用时的各支座反力,见表 5。
| 编号 | 边中跨比 | 跨数 | 弧长/m | 中跨弧长/m | 曲线半径/m |
| A | 1.00 | 3 | 90 | 30 | 500 |
| B | 0.90 | 3 | 90 | 32.2 | 500 |
| C | 0.80 | 3 | 90 | 34.6 | 500 |
| D | 0.70 | 3 | 90 | 37.5 | 500 |
| 半径/m | 边中 跨比 | 支座竖向反力/kN | |||||
| ① | ② | ③ | ④ | ⑤ | ⑥ | ||
| 500 | 1 | 685 | 880 | 3 533 | 3 668 | 671 | 848 |
| 0.9 | 642 | 817 | 3 650 | 3 763 | 627 | 785 | |
| 0.8 | 580 | 731 | 3 795 | 3 913 | 567 | 698 | |
| 0.7 | 510 | 636 | 3 961 | 4 077 | 497 | 605 | |
| 直线 | 1 | 785 | 785 | 3 537 | 3 646 | 767 | 767 |
| 0.9 | 731 | 731 | 3 646 | 3 755 | 713 | 713 | |
| 0.8 | 659 | 660 | 3 790 | 3 899 | 640 | 640 | |
| 0.7 | 577 | 577 | 3 954 | 4 065 | 557 | 557 | |
表 5可以看出,随着边中跨比的减小,边墩支座反力不断减小,中墩支座反力不断增大。在设计中,应避免恒载作用下曲线梁桥边墩内侧支座竖向反力过小,而在运营阶段偏载车辆作用下发生支座脱空。
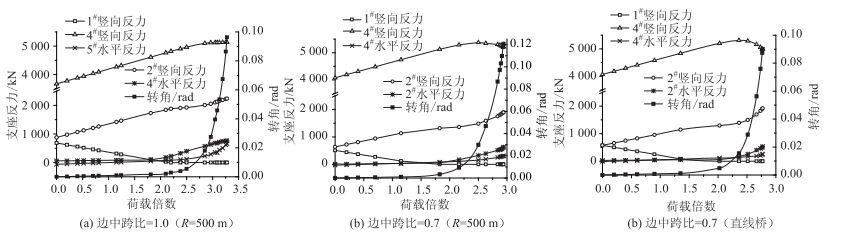
与第2节方法类似,进行公路-Ⅰ级荷载的偏载加载(偏向曲线外侧)。图 7给出不同边中跨比加载至发散全过程中边墩内、外侧支座以及中墩支座的反力变化图(限于篇幅仅给出边中跨比为1.0与0.7的计算结果)。
|
| 图 7 支座反力与转角变化曲线 Fig. 7 Curves of supporting force and rotation |
| |
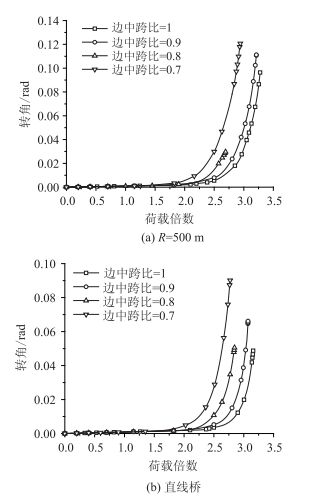
图 7中不同边中跨比时支座反力变化趋势总体相似,但随边中跨比的减小,极限阶段中墩支座竖向反力下降趋势更为明显,而边墩外侧支座竖向反力增大趋势略有增加。也就是说,边中跨比的减小会加剧边墩双支座反力分布的不均匀性。若将不同边中跨比的独柱墩梁桥整体转角随荷载变化的规律绘于图 8,可以看出:随边中跨比的减小,虽然边墩各支座初始反力减小,但当整体侧向转角超限后(大于0.02 rad),边墩外侧支座反力增加更为迅速,提高了由于该支座失稳导致整体结构失效的可能性。也就是说,桥梁全长相同的情况下,减小边中跨比会使独柱墩曲线梁桥更早进入临界倾覆状态。
|
| 图 8 转角变化曲线 Fig. 8 Curves of rotation |
| |
3.2 抗倾覆安全系数
与2.2节类似,不同边中跨比的独柱墩梁桥(R=500 m)和直线桥在相应临界倾覆状态下的安全系数计算结果分别列于表 6。
表 6中可以看出,在桥梁全长及截面形式等设计条件相同的情况下:(1) 对于独柱墩曲线梁桥(R=500 m),采用有限元和规范方法计算,其抗倾覆安全系数均随边中跨比的减小而降低,变化趋势一致,且规范计算结果均小于针对任一临界状态的有限元计算结果。(2) 对于独柱墩直线梁桥,采用有限元计算,其抗倾覆安全系数仍随边中跨比的减小而降低;但采用规范方法计算时,由于倾覆力矩和抗倾覆力矩均保持不变,安全系数仅因为自振频率的不同而有微小差异,且远高于针对任一临界状态的有限元计算结果。
| 半径/m | 边中 跨比 | 支座 脱空 | 整体转角 (0.02 rad) | 倾覆 (计算发散) | 规范方法 |
| 500 | 1 | 1.86 | 2.45 | 2.78 | 1.97 |
| 0.9 | 1.71 | 2.32 | 2.73 | 1.40 | |
| 0.8 | 1.55 | 2.18 | 2.28 | 1.12 | |
| 0.7 | 1.34 | 1.96 | 2.50 | 0.93 | |
| 直线桥 | 1 | 2.01 | 2.56 | 2.68 | 11.41 |
| 0.9 | 1.85 | 2.41 | 2.61 | 11.43 | |
| 0.8 | 1.69 | 2.22 | 2.42 | 11.52 | |
| 0.7 | 1.46 | 2.05 | 2.35 | 11.66 |
综上,当桥梁全长相同时,边中跨比越小的独柱墩梁桥,其抗倾覆安全性能越低;如果同时曲线半径较大,则采用规范方法验算时会大大高估其抗倾覆能力,从而降低结构设计的安全性。
4 结论(1) 对不同曲线半径独柱墩梁桥,随偏载不断增大,边墩内侧支座竖向反力逐渐减小,直至脱空。进而支座反力重新分配,边墩外侧支座竖向反力增速减缓,而中墩单支座竖向反力仍持续增大,最终达到极限状态。
(2) 对于半径较小的(按本文如小于500 m)的独柱墩曲线梁桥,虽然荷载较小时便发生支座脱空,但随后主梁转角变化相对平缓,在荷载持续增大过程中反而具有较好的空间稳定性能。
(3) 无论从支座反力、整体转角还是抗倾覆安全系数来看,对于曲线半径较大的(按本文如大于500 m)的独柱墩梁桥,不能仅依靠现有规范来判定其抗倾覆安全性能,必须结合精细化有限元分析结果进行设计,必要时采取构造措施提高其抗倾覆性能,以保证运营阶段的安全性。
(4) 随边中跨比的减小,当整体侧向转角超限后(大于0.02 rad),边墩外侧支座反力增加更为快速,提高了由于该支座失稳导致整体结构失效的可能性。也就是说,桥梁全长相同的情况下,减小边中跨比会使独柱墩曲线梁桥更早进入临界倾覆状态。
(5) 当桥梁全长相同时,边中跨比越小的独柱墩梁桥,其抗倾覆安全性能越低;如果同时曲线半径较大,则采用规范方法验算时会大大高估其抗倾覆能力,从而降低结构设计的安全性。
(6) 另外,可以采用中墩支座预偏、增大桥墩截面及桥墩两侧增设牛腿以增加支座安置位置,以及增加横向挡块防止倾覆等构造措施降低独柱墩桥梁倾覆的可能性。虽然本文针对普遍应用的3跨连续梁进行分析,由于横向受力是其倾覆的主要原因,故本文结论对大于3跨的独柱墩连续梁也具有一定的适用性。
| [1] | 李盼到, 张京, 王美. 独柱支承梁式桥倾覆稳定性验算方法研究[J]. 世界桥梁, 2012, 40(6): 52-56 LI Pan-dao, ZHANG Jing, WANG Mei. Study of Checking Method for Overturning Stability of Beam Bridge Supported by Single-column Pier[J]. World Bridges, 2012, 40(6): 52-56 |
| [2] | 王钧利. 高墩大跨径连续刚构弯桥全过程稳定性分析[D]. 西安: 长安大学, 2006. WANG Jun-li. Stability Analysis of Long-span Continuous Rigid Frame Bridge with High Piers in Whole Stage[D]. Xi'an: Chang'an University, 2006. |
| [3] | 张敬珍, 徐岳, 黄平明, 等. 宽弯桥变形及控制[J]. 长安大学学报:自然科学版, 2003, 23(2): 64-66 ZHANG Jing-zhen, XU Yue, HUANG Ping-ming, et al. Displacement Control of Wide-curved Bridges[J]. Journal of Chang'an University:Natural Science Edition, 2003, 23(2): 64-66 |
| [4] | JTG D62—2012, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62—2012, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [5] | TB10002. 1—2005, 铁路桥涵设计基本规范[S]. TB10002.1—2005, Fundamental Code for Design on Railway Bridge and Culvert [S]. |
| [6] | BS EN1337—5: 2005, Structural Bearings [S]. |
| [7] | JT/T 391—2009, 公路桥梁盆式支座[S]. JT/T 391—2009, Pot Bearings for Highway Bridges[S]. |
| [8] | 王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007. WANG Xin-min. Numerical Simulation of Engineering Structure Using ANSYS[M]. Beijing: China Communications Press, 2007. |
| [9] | 闫冬, 任胜健, 何勇. 桥梁倒塌模式识别方法:理论分析[J]. 公路交通科技, 2011, 28(8): 100-103 YAN Dong, REN Sheng-jian, HE Yong. Identification Method of Bridge Collapse Pattern: Theoretical Analysis[J]. Journal of Highway and Transportation Research and Development, 2011, 28(8): 100-103 |
| [10] | 闫冬, 任胜健, 何勇. 桥梁倒塌模式识别方法:实例分析[J]. 公路交通科技, 2011, 28(9): 77-80 YAN Dong, REN Sheng-jian, HE Yong. Identification Method of Bridge Collapse Pattern: Analysis of Cases[J]. Journal of Highway and Transportation Research and Development, 2011, 28(9): 77-80 |
| [11] | YOSHIDA J, ABE M, FUJINO Y. Constitutive Model of High-Damping Rubber Materials[J]. Journal of Engineering Mechanics, 2004, 130(2): 129-141 |
| [12] | ALI A, HOSSEINI M, SAHARI B. A Review of Constitutive Models for Rubber-Like Materials[J]. American Journal of Engineering & Applied Sciences, 2010, 3(1): 232-239 |
| [13] | GENT A N. Engineer with Rubber: How to Design Rubber Components[M]. 3rd ed. Cincinnati, US: Hanser Gardner Pubns, 2012. |
| [14] | PENG W, DAI F, TACIROGLU E. Research on Mechanism of Overturning Failure for Single-Column Pier Bridge [C]//Proceedings of International Conference on Computing in Civil and Building Engineering. Orlando, US: American Society of Civil Engineers, 2014:1747-1754. |
| [15] | DENG L, WANG W, YU Y. State-of-the-art Review on the Causes and Mechanisms of Bridge Collapse[J]. Journal of Performance of Constructed Facilities, 2016, 30(2): 1-13 |
| [16] | BARR P J, YANADORI N, HALLING M W, et al. Live-load Analysis of a Curved I-Girder Bridge[J]. Journal of Bridge Engineering, 2007, 12(4): 477-484 |
| [17] | MICHALTSOS G T, RAFTOYIANNIS I G. A Mathematical Model for the Rocking, Overturning and Shifting Problems in Bridges[J]. Engineering Structures, 2008, 30(12): 3587-3594 |
| [18] | WSDOT. WSDOT Bridge Design Manual LRFD[R]. Washington, D.C.: Washington State Department of Transportation, 2016. |
 2017, Vol. 34
2017, Vol. 34
