扩展功能
文章信息
- 王晟, 颜东煌, 周大庆, 廖万辉
- WANG Sheng, YAN Dong-huang, ZHOU Da-qing, LIAO Wan-hui
- 斜拉桥节段纵移悬拼法足尺模型试验研究
- Experimental Study on Full-scale Model of Cable-stayed Bridge Using Sectional Longitudinal Transport and Cantilever Installation Method
- 公路交通科技, 2017, 34(5): 72-79
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(5): 72-79
- 10.3969/j.issn.1002-0268.2017.05.010
-
文章历史
- 收稿日期: 2016-10-25
2. 长沙理工大学 土木与建筑学院, 湖南 长沙 410114;
3. 贵州省公路工程集团有限公司, 贵州 贵阳 550008
2. School of Civil Engineering and Architecture, Changsha University of Science & Technology, Changsha Hunan 410114, China;
3. Guizhou Highway Engineering Group Co., Ltd., Guiyang Guizhou 550008, China
桥梁是道路重要组成部分,大型桥梁往往是山区高速公路建设中的关键性枢纽及控制性工程,其建设工期往往决定着整条线路的工期。随着桥梁科学技术的发展,塔、墩等结构的施工工艺已日趋成熟,其施工工艺优化空间变小,此时主梁架设工艺的优化与革新无疑是缩短建设工期的唯一途径。对于山区大跨度桥梁,由于难以解决主梁节段的整体纵向运输,因此基本都采用散拼法[1-2]进行主梁架设施工。虽然该方法起重量小,杆件的对接、调整、安装方便,但起重设备规模大,空中作业时间长,施工效率低,施工质量不易控制,工期相对较长[3],因此节段整体拼装法优势明显。山区桥梁节段整体拼装常采用轨索移梁工艺[4]或缆索吊机[5-6]架设,两种工艺均能解决主梁节段整体运输和安装问题,施工效率高,空中作业时间短,但轨索移梁工艺是针对于悬索桥研发的工艺,很难应用到山区斜拉桥的主梁施工之中;缆索吊机架设法虽在鸭池河大桥成功应用,但缆索系统的锚固要求高,设备投入巨大,且随着跨径的增大,缆索吊机施工风险增大。
节段纵移悬拼法利用小型机具设备的组合运用,可实现钢桁梁节段的整体提吊、纵向运输及对接拼装,但该工艺在国内外没有成功案例可以借鉴,且梁段自重大,构件间的连接多且复杂,工艺的可行性、各系统的安全可靠性、桁段空中整体拼装的难易程度及结构的动力响应均需要透彻的研究。为此,本文基于北盘江大桥拟定的中跨施工工艺进行了足尺模型试验[7],并基于耦合系统动力学理论,建立了试验结构大系统运动方程,进行了实测数据与计算模拟值的对比,以期验证该工艺的可行性、合理性及安全性。
1 系统组成及足尺模型简介 1.1 系统组成节段纵移悬拼工艺由地面起吊系统、承重系统、运梁系统、运梁小车、临时吊点及桥面吊机组成。运梁系统,见图 1,可看成一道固定在下弦杆下方的轨道梁,其截面形式为HW350×250×9×14;运梁小车,见图 2,配置了8排轮组,每排轮组有独立电机驱动,额定吊装重量为1 200 kN,可进行遥控实现自行行走,负载时可以5~15 m/min两档运行;桥面吊机为后支点式三角桁架体系,后支点锚固于已拼装的上一节段上弦杆,主桁为1.5 m标准贝雷片,斜拉系统由1根刚性竖杆与2根斜拉螺纹钢组成,通过链条驱动位于主桁上的提升吊点实现其纵向移动,并通过横向千斤顶实现吊点横向移动。
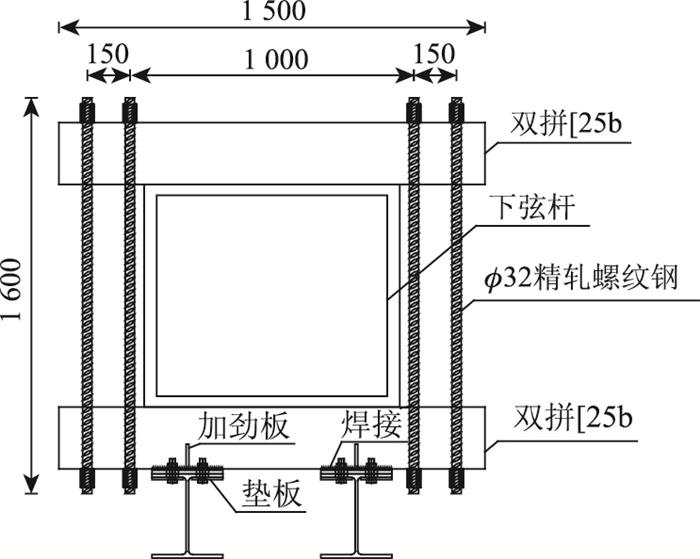
|
| 图 1 运梁系统(单位:mm) Fig. 1 Girder transport system (unit: mm) |
| |
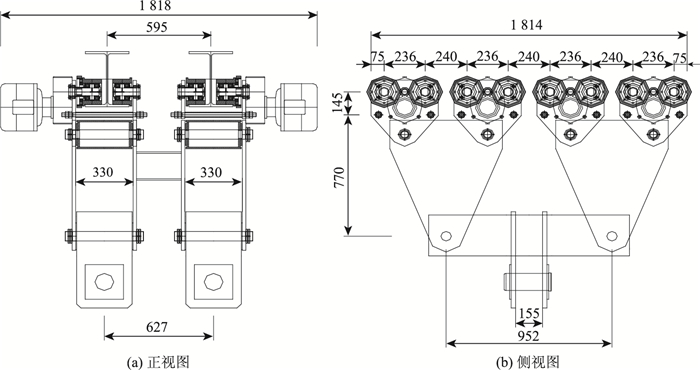
|
| 图 2 运梁小车构造图(单位:mm) Fig. 2 Structure of transport car (unit: mm) |
| |
1.2 模型试验总体布置
选取B1,B2节段作为已拼装节段,选取B3节段作为待拼装节段,将已拼装节段提升并于支架连接,并在已拼装节段上安装桥面吊机。试验共设置4台运梁小车,前、后纵移吊点分别重645.8, 318.5 kN,前、后提升吊点分别重305.5, 658.8 kN。模型试验总体布置见图 3。
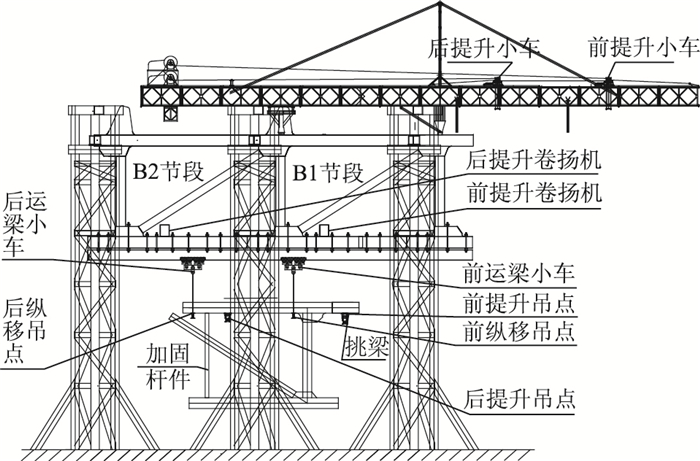
|
| 图 3 模型试验总体布置 Fig. 3 General arrangement of model test |
| |
1.3 试验工况及测点布置 1.3.1 试验工况
工况1:起吊。通过设置在B2节段下弦杆的卷扬机,将B3节段以1 m/min的速度整体提升至预定高度。
工况2:初次吊点转换。连接纵移吊点与运梁小车,随后松开提升吊点完成初次吊点转换。
工况3:运梁小车低速挡(5 m/min)行走。
工况4:运梁小车高速挡(15 m/min)行走。
工况5:提升前吊点受力协同前移。当挑梁伸出后,利用桥机前吊点吊起B3节段前提升吊点,并与运梁小车协同前移。
工况6:二次吊点转换。将吊点由纵移吊点全部转换至提升吊点。
工况7:桥机吊点前移。桥机吊点吊起B3节段以5 m/min的速度前移,直至B3节段完全挑出。
工况8:整体提升。利用桥面吊机整体提升B3节段至预定高度。
工况9:对接。利用桥面吊机的三向微调功能实现B3节段与B1节段的对接。
工况10:高强螺栓安装。
1.3.2 测点布置(1) 加速度测点
加速度传感器位于轨道梁、已拼装节段主桁架及桥面吊机端部,测点布置见图 4。
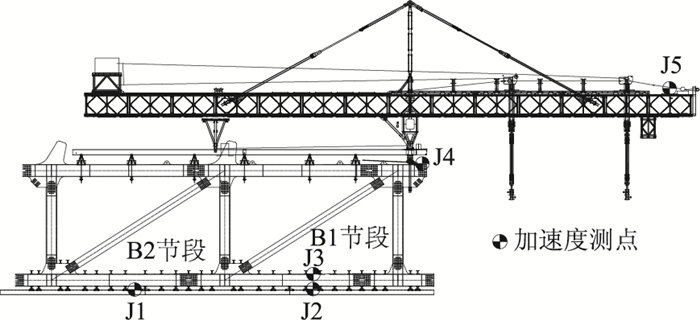
|
| 图 4 加速度测点布置 Fig. 4 Layout of acceleration measuring points |
| |
(2) 应变测点
单条轨道梁共布置7个应变测点,按运梁方向依次为G1~G7,其中G3测点位于1.5 m跨跨中,测点布置见图 5。
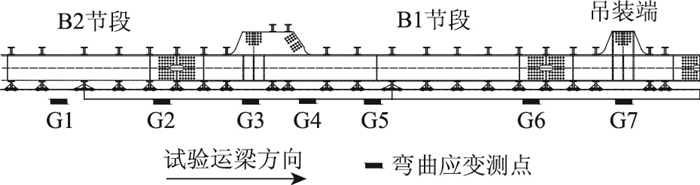
|
| 图 5 轨道梁应变测点布置 Fig. 5 Layout of track strain measuring points |
| |
2 试验过程结构动力响应分析
当待拼装节段提升与前移时,系统可简化为两自由度的弹簧-质量块振动系统,待拼装节段考虑竖向位移和点头2个自由度,运梁系统可简化为多自由度的弹簧振动系统,钢管支架可视为一刚度、阻尼很大的弹簧[8-10]。各工况的系统动力模型见图 6,其中图 6(c)~(e)中未标示出钢管支架的刚度与阻尼。
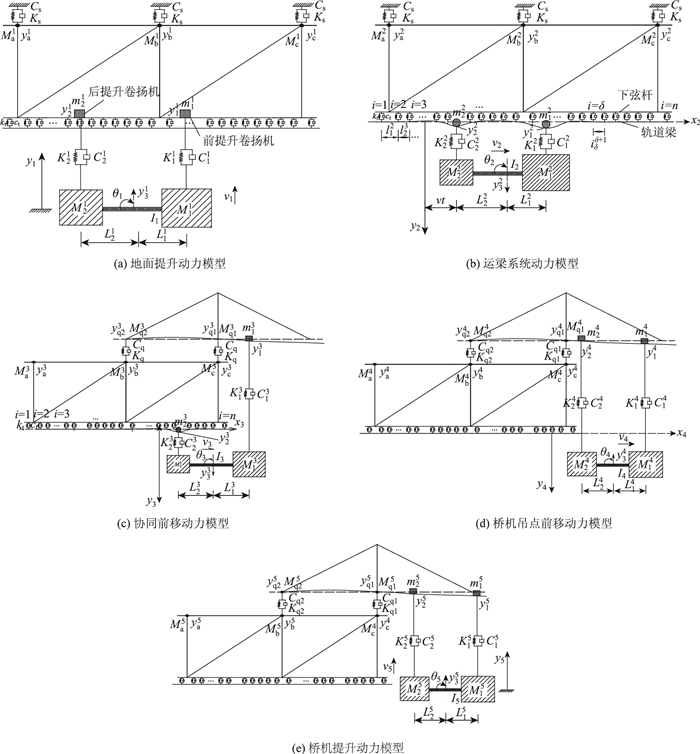
|
| 图 6 系统动力模型 Fig. 6 Dynamic model of system |
| |
在图 6中,t为时间,m1j, m2j(j=1, 2, 3, 4, 5,为状态编号,下同)分别为前、后支承点(卷扬机、运梁小车)质量; M1j, M2j分别为前、后吊点重量; K1j, C1j分别为前吊点钢丝绳的刚度和阻尼; K2j、C2j分别为后吊点钢丝绳的刚度和阻尼;Ks, Cs分别为钢管支架刚度和阻尼; Maj, Mjbjj, Mcj分别为钢管支架分配的既有结构(包括已拼装钢桁梁与桥机)质量; yaj, ybj, ycj分别为支架弹簧的竖向位移;kt, ct分别为单组螺纹钢的刚度和阻尼; lδ, δ+1为第δ组螺纹钢与第δ+1组螺纹钢间距;kt1, kt2[11]分别为前、后运梁小车车轮刚度;Mq1j, Mq2j分别为桥机前、后锚固点分配的重量; yq1j, yq1j分别为桥机前、后锚固点与钢桁梁大节点相对竖向位移;L1j, L2j分别为待拼装节段前、后吊点与节段重心距离; Ij为惯性矩; vj为移动速度; y3j为竖向位移; θj为转角; y1j, y2j分别为前、后吊点所在支承点挠度。此时运梁小车动力平衡方程为:
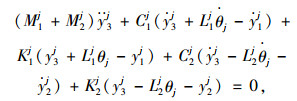
|
(1) |
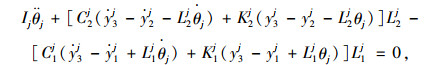
|
(2) |
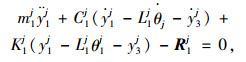
|
(3) |
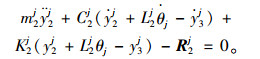
|
(4) |
当为提升工况时,式(3)、(4) 中R1j, R2j为卷扬机与下弦杆或桥机挑臂的作用力向量;当为纵移工况时,R1j, R2j为运梁小车与轨道梁的作用力向量,且R1j=kt1r1,R2j=kt2r2,r1, r2为前后运梁小车所在轨道位置的不平度,方向以向上为正;当为协同前进工况时,R1j为卷扬机与下弦杆或桥机挑臂的作用力向量,R2j为运梁小车与轨道梁的作用力向量。
设运梁系统有n组螺纹钢,第δ组螺纹钢仅承受其前后一半跨度的轨道梁重量,该部分重量为mδ,即:

|
(5) |
式中γ0为轨道梁线容重。
第δ组螺纹钢所在轨道梁截面的挠度为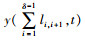
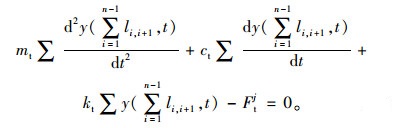
|
(6) |
桥机动力平衡方程为:

|
(7) |
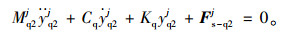
|
(8) |
式中Fs-q1j,Fs-q2j为桥机前、后锚固点与钢桁梁耦合作用力向量。
钢管支架系统动力平衡方程为:
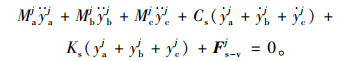
|
(9) |
式中Fs-vj为卷扬机或运梁小车与既有结构耦合作用力向量。
式(1)~(4) 与式(6)~(9) 可写成如下矩阵形式:
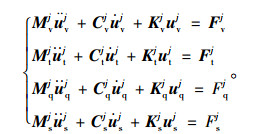
|
(10) |
式中,j=1, 2, 3, 4,分别为4个不同工况;M,C,K和F分别为质量矩阵、阻尼矩阵、刚度矩阵和荷载向量; u,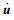
测点加速度幅值见表 1,由于公路桥梁规范中对于加速度的限值规定较少,此处引用在秦沈客运专线综合试验段(设计时速300 km)桥梁的研究和设计中提出的跨中最大允许竖向振动加速度0.35g作为对比值,g为重力加速度。
| 工况号 | 项目 | J1 | J2 | J3 | J4 | J5 | |
| 工况1 | 纵向 | — | — | 75.4 | 44.4 | — | |
| 竖向 | 实测值 | — | — | 133.4 | 56.6 | — | |
| 理论值 | — | — | 106.2 | 47.8 | — | ||
| 工况3 | 纵向 | 613.6 | 664.9 | 107.1 | 44.1 | — | |
| 竖向 | 实测值 | 242.5 | 296.5 | 106.2 | 47.8 | — | |
| 理论值 | 249.3 | 278.3 | 100.4 | 45.1 | — | ||
| 工况4 | 纵向 | 947.1 | 1 023.9 | 140.6 | 64.7 | — | |
| 竖向 | 实测值 | 360.8 | 448.2 | 145.2 | 73 | — | |
| 理论值 | 362.2 | 427.6 | 154.5 | 72.1 | — | ||
| 工况5 | 纵向 | 377.9 | 415.7 | 142.8 | 91.8 | 1 222.7 | |
| 竖向 | 实测值 | 155.7 | 500.1 | 276.6 | 152.4 | 3 002.9 | |
| 理论值 | 158 | 483.4 | 281.2 | 147.1 | 2 932.6 | ||
| 工况7 | 纵向 | — | — | 191.1 | 98.7 | 1 656.3 | |
| 竖向 | 实测值 | — | — | 339.3 | 176.7 | 4 089.4 | |
| 理论值 | — | — | 325.8 | 192.1 | 3 959.5 | ||
| 工况8 | 纵向 | — | — | 156.1 | 100.3 | 1 431.2 | |
| 竖向 | 实测值 | — | — | 273.7 | 164.9 | 3 624.8 | |
| 理论值 | — | — | 265.4 | 173.4 | 3 523.3 | ||
由表 1可知,测点的加速度幅值与其所在位置有关,相同工况下不同测点的加速度幅值差异性较大,同时,相同测点在不同工况下的加速度幅值也有一定差别;轨道梁测点的最大实测加速度幅值均表现为纵向,并于工况4达到最大,此时J1, J2测点幅值分别为664.9, 966.9 mm/s2;钢桁梁测点的最大实测加速度幅值均表现为竖向,并于工况7达到最大,此时J3, J4测点幅值分别为339.3, 176.7 mm/s2;由于桥面吊机为悬臂结构,其悬臂端部测点振动较大,实测加速度幅值于工况7达到最大,为4 089.4 mm/s2,表现为竖向,最大竖向加速度为0.212g,小于0.35g。同时,工况4较工况3各测点加速度幅值明显增大,其中工况4中J1, J2的纵向加速度实测幅值较工况3增大约54%,竖向加速度实测幅值增大约51%,J3的纵向加速度实测幅值较低速档增大约31%,竖向加速度实测幅值增大约36%,这说明运梁小车移动速度对结构的冲击效应影响较为显著,且结构不同位置、不同方向对运梁小车移动速度的敏感程度不同;测点理论计算所得竖向加速度幅值与实测幅值吻合较好,相差最大的为工况3的J3测点,误差为5.6%。
3.2 应力工况3,4的轨道梁各应变测点实测峰值与理论值对比见图 7。

|
| 图 7 各测点应力峰值 Fig. 7 Peak stress of each measuring point |
| |
由图 7可知,轨道梁最大应力峰值出现在G3测点,工况3时G3实测应力峰值为114.7 MPa,最大应力理论值为105.6 MPa,工况4时G3实测应力峰值为118.3 MPa,最大应力理论值为108.7 MPa;测点应力峰值与其所处轨道梁跨度基本呈正比例关系,轨道梁各测点实测应力峰值均在安全范围内,运梁系统能满足高速载重行走,且理论应力峰值与实测值吻合较好。工况4与工况3应力峰值之比见表 2。
由表 2可知,运梁小车高速档运行时轨道梁应力峰值均较低速档有所增大,轨道梁不同应力测点对车速的敏感程度不同,其中G3测点对车速相对最为敏感,其高速档应力峰值约为低速档的1.03倍,G2,G6测点对车速相对不敏感,其高速档应力峰值约为低速档的1.02倍。
| 测点号 | 比值 | |
| 实测值 | 理论值 | |
| G1 | 1.028 | 1.027 |
| G2 | 1.018 | 1.017 |
| G3 | 1.031 | 1.029 |
| G4 | 1.026 | 1.029 |
| G5 | 1.023 | 1.023 |
| G6 | 1.017 | 1.019 |
| G7 | 1.027 | 1.026 |
3.3 试验消耗及过程描述
足尺模型试验各工况所消耗时间及工人数见表 3。
| 工况 | 时间/min | 工人数 |
| 工况1 | 15 | 6 |
| 工况2 | 24 | 6 |
| 工况3 | 3 | 2 |
| 工况4 | 1 | 2 |
| 工况5 | 12 | 6 |
| 工况6 | 138 | 6 |
| 工况7 | 26 | 4 |
| 工况8 | 34 | 4 |
| 工况9 | 23 | 12 |
| 工况10 | 167 | 16 |
由表 3可知,工况10耗时最长,且需要16人配合施工,但螺栓安装属于常规施工,并不是施工工艺能够改善的;由于前提升吊点原设计复杂,导致工况6耗时138 min,存在较大优化空间;桥面吊机三向微调功能可实时调整钢桁梁的空间位置,为钢桁梁整体对接的快速、顺利完成提供了基础,整个对接作业仅耗时23 min;运梁小车稳定、可靠,在行进过程中速度均匀,未出现停车、蛙跳及不同步现象。此外,试验过程平稳,工况间的衔接顺利、连贯性较好;施工组织流程合理,整节段地面提升、运输、拼装可在一天内完成,较散件拼装法工期优势明显。
4 结论足尺模型试验于2014年12月开始架设试验支架,并于2015年8月2日至2015年8月20日进行了试验。通过此次足尺模型试验可以得出以下结论:
(1) 主梁节段提升后交给运梁小车,运梁小车将节段运送至安装位置,桥面吊机完成整体提升及对接拼装,施工组织流程合理。同时结构加速度幅值较小,试验过程平稳,工序间的衔接顺利,验证了节段纵移悬拼法的可行性、合理性及安全性,节段纵移及整体对接耗时短,较散拼法工期优势明显。
(2) 运梁小车机动性能良好,实现了梁段运输的自动化,运梁系统稳定性较好,能满足小车载重高速行走;桥面吊机的三向微调功能在节段整体对接过程中起到了关键作用。
(3) 测点理论竖向加速度幅值、理论轨道梁应力峰值与实测值吻合较好,验证了理论模型的准确性,运梁小车高速挡行走时对结构的冲击效应较低速挡大,不同测点对车速的敏感程度不同,桥机吊点前移过程中系统的振动最为显著。
(4) 由于前提升吊点构造复杂,在二次吊点转换中耗费了较多时间,存在较大优化空间。
| [1] | 刘高, 彭运动, 周平, 等. 坝陵河大桥钢桁加劲梁施工架设方案研究[J]. 公路交通科技, 2009, 26(5): 80-90 LIU Gao, PENG Yun-dong, ZHOU Ping, et al. Research on Erection Methods of Steel Stiffening Truss Girder for Baling River Bridge[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 80-90 |
| [2] | 李键, 蔡向阳. 果子沟特大桥上部结构设计与施工[J]. 公路, 2012(5): 113-117 LI Jian, CAI Xiang-yang. Design and Construction of Supperstructure of Guozigou Long Span Bridge[J]. Highway, 2012(5): 113-117 |
| [3] | 秦顺全. 武汉天兴洲公铁两用长江大桥关键技术研究[M]. 北京: 人民交通出版社, 2009. QIN Shun-quan. Study of Key Technologies for Wuhan Tianxingzhou Rail-cum-road Yangtze River Bridge[M]. Beijing: China Communications Press, 2009. |
| [4] | 潘权. 塔梁分离式悬索桥轨索移梁工艺施工过程静力分析及试验研究[D]. 长沙: 长沙理工大学, 2015. PAN Quan. Mechanical Analysis and Experimental Research on Rail Cable Launching Technology about Suspension Bridge with Separated Tower and Stiffening Girder [D]. Changsha: Changsha University of Science & Technology, 2015. |
| [5] | 王碧波, 易伦雄. 镇胜公路北盘江大桥钢桁梁架设方案研究[J]. 桥梁建设, 2009(3): 48-50 WANG Bi-bo, YI Lun-xiong. Research of Erection Scheme for Steel Truss Girder of Beipan River Bridge on Zhenning-Shengjingguan Expressway[J]. Bridge Construction, 2009(3): 48-50 |
| [6] | 刘世明, 刘永健, 姚晓荣, 等. 钢管混凝土拱桥缆索吊装施工优化[J]. 公路交通科技, 2012, 29(7): 70-75 LIU Shi-ming, LIU Yong-jian, YAO Xiao-rong, et al. Optimization of Cable-hoisting Erection of Concrete-filled Steel Tubular Arch Bridge[J]. Journal of Highway and Transportation Research and Development, 2012, 29(7): 70-75 |
| [7] | 颜东煌, 王晟, 母进伟, 等. 节段纵移悬拼法足尺模型试验动载效应研究[J]. 中国公路学报, 2016, 29(11): 57-64 YAN Dong-huang, WANG Sheng, MU Jin-wei, et al. Research on Dynamic Load Effect in Full-scale Model Test of Sectional Longitudinal Transport and Cantilever Installation Method[J]. China Journal of Highway and Transport, 2016, 29(11): 57-64 |
| [8] | 翟婉明, 夏禾. 列车-轨道-桥梁动力相互作用理论与工程应用[M]. 北京: 科学出版社, 2011. ZHAI Wan-ming, XIA He. Train-track-bridge Dynamic Interaction Theory and Engineering Application[M]. Beijing: Science Press, 2011. |
| [9] | ZAKERI J A, XIA H. Dynamic Analysis of Steel Bridges under Moving Train Loads[J]. Journal of Transportation Research, 2005, 1(2): 27-34 |
| [10] | XIA H, ZHANG N, ROECK D G. Dynamic Analysis of High Speed Railway Bridge under Articulated Trains[J]. Computers & Structures, 2003, 81(26/27): 2467-2478 |
| [11] | 臧利国, 赵又群, 李波, 等. 非充气机械弹性车轮静态径向刚度特性研究[J]. 兵工学报, 2015, 36(2): 355-362 ZANG Li-guo, ZHAO You-qun, LI Bo, et al. Static Radical Stiffness Characteristics of Non-pneumatic Mechanical Elastic Wheel[J]. Acta Armamentarii, 2015, 36(2): 355-362 |
| [12] | CJJ 166—2011, 城市桥梁抗震设计规范[S]. CJJ 166—2011, Code for Seismic Design of Urban Bridge[S]. |
| [13] | 王新敏. ANSYS结构动力分析与应用[M]. 北京: 人民交通出版社, 2014. WANG Xin-min. Structural Dynamic Analysis and Application with ANSYS[M]. Beijing: China Communications Press, 2014. |
| [14] | 李小珍, 喻璐, 强士中. 不同主梁竖曲线下大跨度斜拉桥的车桥耦合振动分析[J]. 振动与冲击, 2003, 22(2): 43-46 LI Xiao-zhen, YU Lu, QIANG Shi-zhong. Vehicle-bridge Interaction of Long-span Cable-stayed Bridges with Various Vertical Girder Curves[J]. Journal of Vibration and Shock, 2003, 22(2): 43-46 |
| [15] | 田仲初, 陈耀章. 三塔斜拉桥索塔锚固区节段足尺模型试验[J]. 公路交通科技, 2013, 30(7): 89-96 TIAN Zhong-chu, CHEN Yao-zhang. Full-scale Model Experiment on Cable Pylon Anchorage Zone of 3-pylon Cable-stayed Bridge[J]. Journal of Highway and Transportation Research and Development, 2013, 30(7): 89-96 |
| [16] | 鲁乃唯. 随机车流下悬索桥加劲梁动力响应概率模型与可靠度研究[D]. 长沙: 长沙理工大学, 2014. LU Nai-wei. Probability Model of Dynamic Responses and Reliability Assessment for Stiffening Girders of Suspension Bridges under Random Traffic Flow [D]. Changsha: Changsha University of Science & Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10536-1015393309.htm |
| [17] | 周凌宇, 贺桂超. 大跨度钢-混凝土组合桁架铁路桥端节点模型试验研究[J]. 土木工程学报, 2012, 45(1): 92-99 ZHOU Ling-yu, HE Gui-chao. Model Test for the End Joint of Long-span Steel-concrete Composite Truss RAILWAY Bridges[J]. China Civil Engineering Journal, 2012, 45(1): 92-99 |
| [18] | 闫勇, 沈锐利, 唐茂林, 等. 轨索滑移法节段足尺模型试验研究[J]. 桥梁建设, 2013, 43(2): 46-50 YAN Yong, SHEN Rui-li, TANG Mao-lin, et al. Testing Study of Full-sale Sectional Model for Rail Cable Launching Method[J]. Bridge Construction, 2013, 43(2): 46-50 |
| [19] | 宋旭明, 戴公连, 方淑君. 三汊矶湘江大桥整体模型试验[J]. 中国公路学报, 2009, 22(1): 53-59 SONG Xu-ming, DAI Gong-lian, FANG Shu-jun. Total Bridge Model Test of Sanchaji Xiangjiang Bridge[J]. China Journal of Highway and Transport, 2009, 22(1): 53-59 |
 2017, Vol. 34
2017, Vol. 34
