扩展功能
文章信息
- 龙尧, 张家生, 陈俊桦
- LONG Yao, ZHANG Jia-sheng, CHEN Jun-hua
- 基于Weibull分布的土-结构接触面剪切损伤模型研究
- Study on Shear Damage Model for Soil-structure Interface Based on Weibull Distribution
- 公路交通科技, 2017, 34(5): 65-71
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(5): 65-71
- 10.3969/j.issn.1002-0268.2017.05.009
-
文章历史
- 收稿日期: 2016-07-01
工程中土与结构物如土与挡土墙,土与桩,土与堆石坝等相互作用较为常见,研究二者相互作用的问题具有现实意义。目前针对上述接触面相互作用问题的研究主要集中在土颗粒沿接触面滑移时的力学行为。基于合理的土-接触面剪切本构模型的数值仿真有助于深入认识土-接触面剪切滑移力学行为,并对土-接触面剪切力学规律进行预测,因而接触面剪切力学模型是广大学者的研究热点。
土-接触面剪切本构关的试验基础一般为直剪试验。胡黎明等[1]利用直剪试验仪研究砂土与具有粗糙度钢板的接触面剪切特性。冯大阔等[2]利用直剪试验研究粗粒土与钢板接触面上的剪切力学性质。陈俊桦等[3]利用大型直剪仪研究了红黏土-混凝土接触面力学特性。现有文献[4]表明,土-结构接触面剪应力-应变关系一般呈明显的非线性关系。静力作用下,用于描述这种特点的力学模型主要有非线性弹性模型和弹塑性模型。如著名的Duncan-Chang[5]双曲线模型为非线性弹性模型。但是,非线性弹性模型不能描述应力应变软化的性质,因而一些学者采用弹塑性模型:Gómez等[6]基于直剪试验定义了循环荷载作用下的接触面亚塑性本构模型。张嘎等[7]针对粗颗粒土-结构接触面的剪切特性,通过单剪和循环剪切试验提出了弹塑性理论条件下的统一接触面弹塑性模型。
然而,由于土体本身力学性质的复杂性,通过室内试验拟合得到的一些弹塑性数学模型一般适用范围较窄。一般可通过曲线拟合的方式在理论曲线逼近试验结果的情况下确定模型相关参数,但这样的方法使得相关参数的物理意义不明确。现有研究表明,土-混凝土结构接触面上剪应力应变关系表现主要为应变软化[8]。近年来,统计损伤理论在固体力学尤其是岩石工程领域应用较广。曹文贵等[9-10]建立了基于Weibull随机分布的岩石统计损伤软化本构模型,并进一步发展了考虑岩石体积变化因素的岩石应变软硬化损伤模型。基于统计损伤理论的岩石本构模型能较好地反映岩石软化性质,模型参数来自试验统计结果,克服了因非均质性等随机因素给岩土材料力学行为带来的不确定性影响,同时确定的模型参数具有明确的物理意义。目前,将统计损伤理论引入到土的力学行为研究中的文献较少,应用到土-结构接触面剪切行为的研究更少。张嘎等[11]根据粗粒土与结构接触面的受载特性,提出了土与结构接触面的损伤本构模型。胡黎明等[12]根据粗糙接触面的变形机理,建立了基于损伤力学理论的接触面本构模型。
从上述研究可以看出,从损伤角度构建结构接触面的力学模型能够较好地描述土-结构接触面的相互作用机理。因此,为了研究土-结构接触面剪切损伤机理,文中基于统计损伤理论提出土-结构物接触面剪切损伤模型,并通过室内直剪试验获得模型参数,最后对模型的合理性进行了验证, 证明了剪切损伤模型能够充分反映土-结构接触面软化特性和应力状态,具有广泛的工程应用前景,为土-结构接触面力学性质的深入研究提供参考。
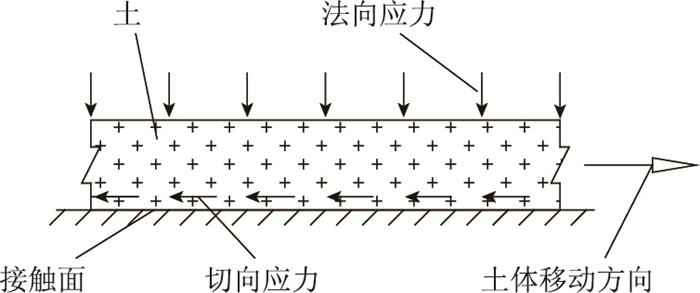
1 剪切损伤模型建立 1.1 剪切损伤模型假定土-结构接触面剪切力学行为的研究实质上是针对接触面附近薄层土,即剪切厚度而言的。一般来说,接触面剪切过程主要的变形提供载体为土而不是结构物,如土与混凝土结构物接触时,沿接触面的剪切变形由接触面附近薄层土体提供。因此,针对土-结构接触面剪切过程的研究一般立足于土体本身的力学属性。文献[13-14]研究成果揭示了达到剪应力在峰值后,黏性土-混凝土结构接触面剪应力应变关系呈软化现象。土-结构接触面剪切加载示意图见图 1。接触面软化过程实际上就是一种损伤过程,为引入损伤力学理论进行分析的基本假设如下:
|
| 图 1 土-结构接触面加载示意图 Fig. 1 Schematic diagram of loading for soil-structure interface |
| |
(1) 目前研究土的力学模型大多假设土为各向同性连续介质。为方便应用连续介质理论,假定土体为各向同性损伤材料。
(2) 在外力作用下,损伤土体包括未损伤部分和损伤部分。某微元作用面上总荷载由无损部分承担。无损部分承受的应力为有效应力。
(3) 土体沿接触面切向滑移过程为剪切损伤过程。当损伤发展到一定程度,接触面上剪切应力达到破坏强度。此后,应力应变关系由初始非线性递增向应变软化转化。
(4) 岩石等固体材料存在与初始损伤对应的临界应力或应变水平。在加载水平未达到临界值时,岩石材料一般为线弹性。本构关系为线弹性时,不反生损伤。只有达到临界值时,损伤才会发展[3, 9]。土与岩石不同,土的线弹性范围很小。故假设土的损伤发展伴随着整个剪切加载过程。
1.2 剪切损伤模型推导由假设(1)~(2) 可知,接触面上剪切应力满足[12]:
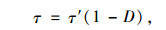
|
(1) |
式中,τ为名义剪应力;τ′为不考虑损伤影响的有效剪应力,变量上标“′ ”表示该变量的有效值;D为损伤变量,为标量,表征接触面力学性质的劣化,D=1时,接触面附近薄层土完全丧失抵抗力。
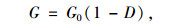
|
(2) |
式中,G为加载过程中割线剪切模量;G0为初始剪切模量。
以有效应力表示的剪切本构方程为[16]:
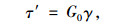
|
(3) |
式中γ为剪切应变,即为剪切相对位移与剪切厚度的比值。
考虑到试验中应力数据一般为名义值,根据式(1) 和式(3),得到名义剪切应力表示的接触面剪切变形本构关系如下:
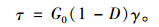
|
(4) |
根据现有文献的研究结果[12, 16],接触面破坏强度满足Weibull分布统计规律,此时损伤变量计算为:
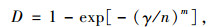
|
(5) |
式中,0≤D≤1;γ≥0;m和n为Weibull分布函数的参数。
从式(5) 看出,加载时,当γ从0开始不断增加时,表征接触面力抵抗力劣化的损伤变量D也从0开始不断增加, 即损伤发展伴随加载整个过程。可见式(5) 满足假设条件(4)。
由式(4) 和式(5) 得到基于统计强度理论的损伤本构关系:
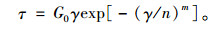
|
(6) |
接触满足面剪切破坏摩尔-库伦屈服准[3, 8]。当剪切强度达到峰值或临界最大值时,应力强度函数表达式为:
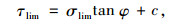
|
(7) |
式中,τlim为临界剪切应力,为剪切破坏强度;σlim为与临界剪切应力对应的法向应力;φ和c分别为接触界面的摩擦角和黏聚力。
由式(4)~(7),得到与临界最大剪应力对应的临界剪切应变为:
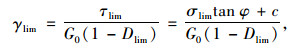
|
(8) |
式中,γlim为与临界最大剪应力τlim对应的临界剪切应变;Dlim为与临界最大剪应力τlim对应的临界损伤变量。
1.3 损伤本构模型参数确定基上分析可知,损伤本构模型的参数为:G0,φ,c,n,m和Dlim, 其中φ和c为强度参数,n,m和Dlim为模型计算参数。根据式(7),由τlim和σlim可通过回归分析的方法得到φ和c。根据式(7),求得临界损伤变量为:
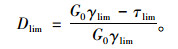
|
(9) |
由于应变软化模型存在峰值,因此,式(6) 存在最大值, 即剪切损伤软化模型满足:
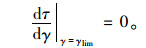
|
(10) |
由式(6) 和式(10),得到:
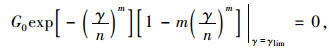
|
(11) |
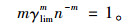
|
(12) |
将式(12) 代入式(6) 后,有如下关系:
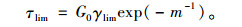
|
(13) |
由联立式(7) 和式(11) 可确定m和n。
目前,针对岩土材料的模型及参数研究一般基于试验结果。常用的方法为使理论曲线和试验曲线满足一定的吻合度,从而得到相关参数。这种方法带来的问题是相关参数的物理意义不明确或者没有物理意义。而从式(9)~(11) 及相关叙述可知,文中提出的损伤模型的相关参数的物理意义是明确的。模型参数m和n值通过试验曲线的拟合得到,而不能通过试验直接得到,通常需建立与试验参数的关系式得到。
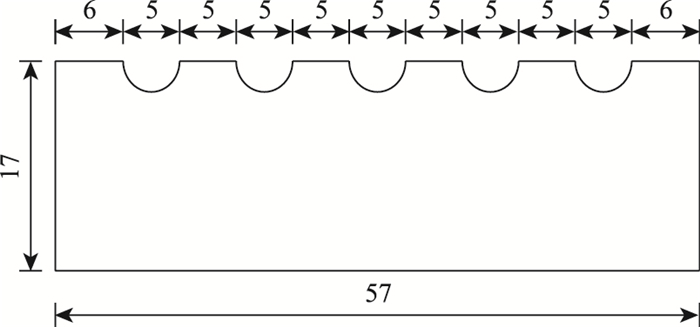
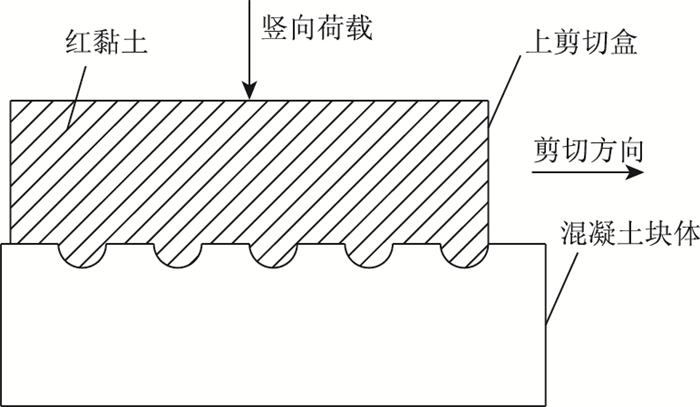
2 模型参数的试验研究 2.1 试验设备及方案目前针对土-结构接触面力学性质的研究一般采用直剪试验。文中采用直剪试验研究确定模型参数。试验仪器设备为中南大学高速铁路建造技术国家工程实验室内的TYJ-800大型直接剪切仪[3]。试验研究对象为红黏土-混凝土结构接触面力学性质。试验土样为红黏土,取样来自湖南省长沙市区。重塑后的红黏土土样的物理参数为:红黏土最大干密度为1.81 g/cm3,最优含水率为14.08%,塑性指数为21,液性指数为0.304。红黏土样三维尺寸为50 cm×50 cm×15 cm。混凝土制块表面预制半圆凹槽,使得混凝土块体表面具备一定的起伏度。自制的混凝土块体外观几何尺寸57 cm×57 cm×17 cm。几何尺寸平面图见图 2。图 2中表面半圆凹槽直径为5 cm,长57 cm。试验时,剪切速率约为1 mm/min,含水率采用最佳含水率。试验中设置4个法向应力水平σ,取值分别为σ=100,200,400,600 kPa。试验加载示意图见图 3。
|
| 图 2 混凝土块体平面示意图(单位:cm) Fig. 2 Schematic diagram of plane of concrete block (unit: cm) |
| |
|
| 图 3 试验加载过程示意图 Fig. 3 Schematic diagram of loading during testing |
| |
2.2 试验结果及分析
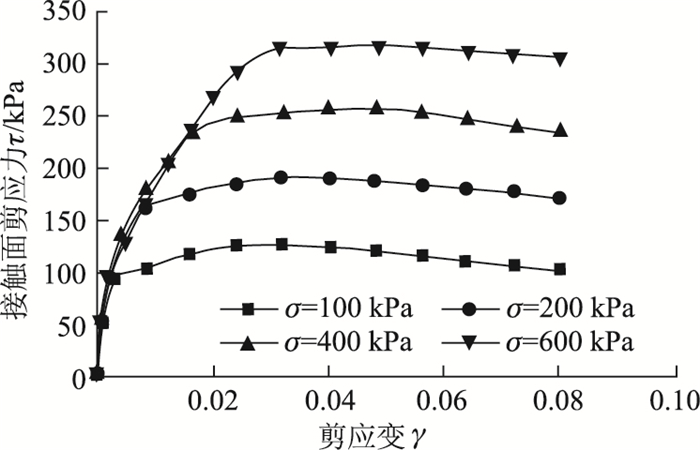
直剪试验一般是取得相对剪切位移与剪切应力之间的关系,由于是试验得出而广泛应用。但是殷宗泽等[17]通过接触面试验证明,对剪切位移与剪切应力之间的关系是特定尺寸的试验剪切破坏过程逐步发展的宏观反映,不能用来表示接触面上剪切变形的普遍规律,而应该考虑剪切厚度的影响。Desai等[18]曾提出剪切厚度比率的概念,即接触面剪切厚度与接触面长度的比值,他认为剪切厚度比率为1/100~1/10比较合理,但是此范围过大,不利于取值。殷宗泽等[19]提出当接触面长度小于1 m时,剪切厚度比率取1/20~1/10比较合理。本文剪切厚度比率取1/10。不同法向应力水平下的剪切应力应变曲线见图 4。从图 4看出,峰值剪应力随着法向应力的增大而增大。随着法向应力的增大,接触面最大剪应力对应的剪应变变大。峰值强度后,应力应变关系呈应变软化或者弱软化趋势。弱软化趋势是指随着法向压力的增加,应力应变软化关系随之弱化。总体来说,黏性土-结构接触面剪切应变关系曲线为应变软化型。通过试验得到接触面剪应力-应变曲线的特征参数见表 1。从表 1看出,随着法向应力水平增大,临界剪应力、临界剪应变和初始剪切模量均增大。
|
| 图 4 接触面剪应力-应变曲线 Fig. 4 Curves of shear stress-strain on interface |
| |
| 临界法应力 σlim/kPa | 临界剪应力 τlim/kPa | 临界剪应变 γlim | 初始剪切模量 G0/MPa |
| 100 | 127.4 | 0.027 | 46 |
| 200 | 191.7 | 0.038 | 76 |
| 400 | 257.7 | 0.047 | 218 |
| 600 | 318.6 | 0.051 | 224 |
根据式(8),通过统计回归分析得到剪切强度参数,见表 2。回归数据相关性系数为0.983,数据相关性良好。
由式(9)~(10) 得到损伤模型的相关计算参数,见表 3。从表 3可以看出,临界损伤值接近于1。而脆性岩石材料的临界损伤值一般为0.2~0.5,且脆性越明显,临界损伤值越小[9-10]。这表明,黏性土-接触面剪切损伤过程为延性破坏过程。
| σ/kPa | Dlim | n | m |
| 100 | 0.89 | 0.004 145 | 0.439 1 |
| 200 | 0.94 | 0.002 537 | 0.368 7 |
| 400 | 0.98 | 0.000 386 | 0.271 5 |
| 600 | 0.97 | 0.000 531 | 0.279 4 |
2.3 模型参数修正
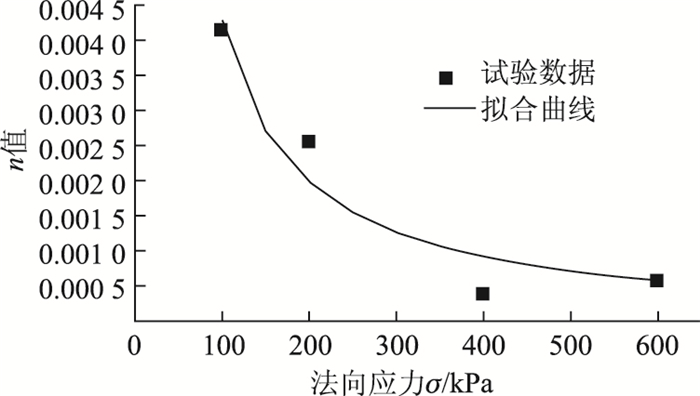
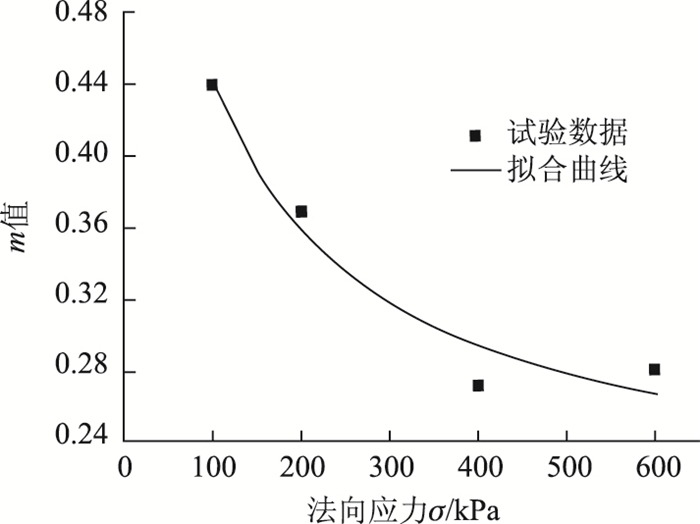
根据表 3可以看出n和m值随法向应变而变化,如果分别以n与m为纵坐标,法向应力为横坐标,可以得到n-σ与m-σ散点分布图,如图 5和图 6所示。分别用幂函数和双曲线拟合可得:
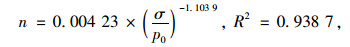
|
(14) |
式中P0为标准大气压,101 kPa。
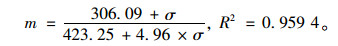
|
(15) |
|
| 图 5 Weibull分布参数n随法向应力σ变化关系 Fig. 5 Weibull distribution parameter n varying with normal stress σ |
| |
|
| 图 6 Weibull分布参数m随法向应力σ变化关系 Fig. 6 Weibull distribution parameter m varying with normal stress σ |
| |
将式(14) 和式(15) 代入式(5),然后将式(5) 代入式(6) 即可得到修正后剪切损伤模型。
3 模型验证采用建议的土-结构接触面剪切损伤模型,采用已有直剪试验成果进行拟合分析,验证文中建议的剪切损伤模型的合理性。
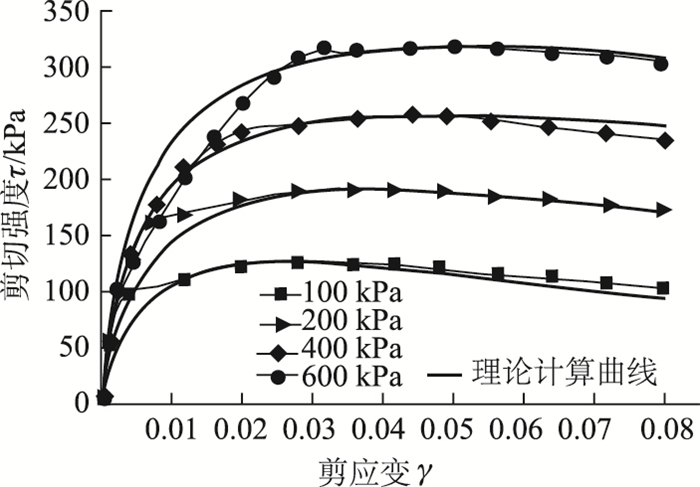
3.1 黏性土-结构接触面直剪试验成果拟合利用文中建议的土-结构接触面剪切损伤模型,可得到与文中直剪试验控制条件相同时的理论计算曲线。损伤模型计算得到的剪切应力应变曲线与试验得到的曲线对比见图 7。分析图 7可知,由于土体本身的复杂性等因素的影响,试验结果和理论计算结果并不完全吻合,但整体上试验曲线和理论曲线吻合度较好。因此,损伤理论模型所需的参数数据精度合适,且理论模型适合描述黏性土-结构接触面面剪切破坏过程。模型真实反映了峰值剪应力随法向应力增大而增大的应力状态。
|
| 图 7 不同法向应力条件下试验曲线与理论曲线的比较 Fig. 7 Comparison between experimental and theoretical curves under different normal stresses |
| |
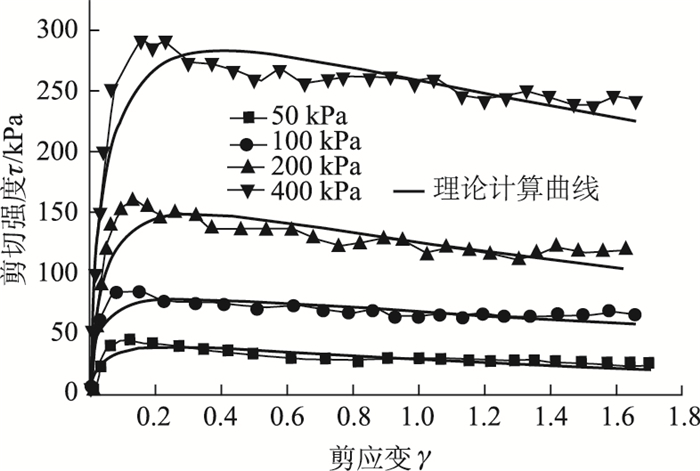
|
| 图 8 不同法向应力条件下试验曲线与理论曲线的比较(胡黎明2001年) Fig. 8 Comparison between experimental and theoretical curves under different normal stresses (Hu Li-ming, 2001) |
| |
3.2 砂土-结构接触面直剪试验成果拟合
文献[1]对砂土与钢板接触面的剪切特性进行了直剪试验研究。试验中砂样的相对密度Dr为90%,相对粗糙度R为0.2,砂样的三维尺寸为60 mm×50 mm ×30 mm,接触面法向应力为50, 100, 200, 400 kPa。剪切厚度比率取1/10,得到了不同法向应力下接触面剪切应力和剪切应变的关系曲线,可以看出砂土与钢板接触面剪切过程中有明显的软化现象。采用文中建议的剪切损伤模型对试验结果进行拟合,如图 8所示,模型能够较好地反映砂土-结构接触面的软化特性以及应力状态,表明该模型具有良好的预测效果。
4 结论文中以红黏土和混凝土块体为试验材料,结合大型直剪试验,研究黏性土-结构接触面剪切力学性质。提出了基于Weibull分布的土-结构接触面剪切损伤模型,并确定了损伤模型参数,最后验证了模型的合理性。
(1) 峰值剪应力随着法向应力的增大而增大。到达剪切破坏强度后,剪应力应变关系为应变软化。随着法向应力的增大,黏性土-结构接触面剪切软化现象变得不显著。
(2) 所提出的剪切损伤模型参数少、物理意义明确,且采用由试验结果反演得出的模型参数后,理论模型曲线与直剪试验曲线较为吻合,提出的接触面剪切损伤模型合理。
(3) 模型参数n和m值受法向应力的影响,通过构建与法向应力的关系式,表明n, m与法向应力分别呈非线性关系。
综上所述,文中建议的土-结构接触面剪切损伤模型能够较好地拟合接触面直剪试验的成果,客观反映接触面应变软化特性和应力状态,其合理性得到了验证。
| [1] | 胡黎明, 濮家骝. 土与结构物接触面物理力学特性试验研究[J]. 岩土工程学报, 2001, 23(4): 431-435 HU Li-ming, PU Jia-liu. Experimental Study on Mechanical Characteristics of Soil-structure Interface[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 431-435 |
| [2] | 冯大阔, 侯文峻, 张建民. 粗粒土与结构接触面三维力学特性的直剪试验研究[J]. 土木工程学报, 2012, 45(5): 169-175 FENG Da-kuo, HOU Wen-jun, ZHANG Jian-min. Large-scale Direct Shear Test Investigation of the 3D Behavior of a Gravel-structure Interfaces[J]. China Civil Engineering Journal, 2012, 45(5): 169-175 |
| [3] | 陈俊桦, 张家生, 李键. 考虑粗糙度的黏性土-结构接触面力学特性试验[J]. 四川大学学报:工程科学版, 2015, 47(4): 22-30 CHEN Jun-hua, ZHANG Jia-sheng, LI Jian. Experimental Research on Mechanical Characteristics of Cohesive Soil-structure Interface by Considering Its Roughness[J]. Journal of Sichuan University: Engineering Science Edition, 2015, 47(4): 22-30 |
| [4] | 孙海忠, 黄茂松. 考虑粗粒土应变软化特性和剪胀性的本构模型[J]. 同济大学学报:自然科学版, 2009, 37(6): 727-732 SUN Hai-zhong, HUANG Mao-song. A Constitutive Model for Coarse Granular Material Incorporating Both Strain Work-softening and Dilatancy[J]. Journal of Tongji University: Natural Science Edition, 2009, 37(6): 727-732 |
| [5] | DUNCAN J M, CHANG C Y. Nonlinear Analysis of Stress and Strain in Soils[J]. Journal of the Soils Mechanics and Foundation Division, 1970, 96(5): 1629-1633 |
| [6] | GóMEZ J E, FILZ G M, EBELING R M. Extended Hyperbolic Model for Sand-to-concrete Interfaces[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(11): 993-1000 |
| [7] | 张嘎, 张建民. 粗粒土与结构接触面统一本构模型及试验验证[J]. 岩土工程学报, 2005, 27(10): 1175-1179 ZHANG Ga, ZHANG Jian-min. Unified Modeling of Soil-structure Interface and Its Test Confirmation[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(10): 1175-1179 |
| [8] | 赵春风, 龚辉, 赵程, 等. 考虑法向应力历史的黏土-混凝土界面弹塑性分析[J]. 岩石力学与工程学报, 2012, 31(4): 848-855 ZHAO Chun-feng, GONG Hui, ZHAO Cheng, et al. Elastoplastic Analysis of Interface between Clay and Concrete Considering Effect of Normal Stress History[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(4): 848-855 |
| [9] | 曹文贵, 赵衡, 张玲, 等. 考虑损伤阀值影响的岩石损伤统计软化本构模型及其参数确定方法[J]. 岩石力学与工程学报, 2008, 27(6): 1148-1154 CAO Wen-gui, ZHAO Heng, ZHANG Ling, et al. Damage Statistical Softening Constitutive Model for Rock Considering Effect of Damage Threshold and Its Parameters Determination Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1148-1154 |
| [10] | 曹文贵, 赵衡, 张永杰, 等. 考虑体积变化影响的岩石应变软硬化损伤本构模型及参数确定方法[J]. 岩土力学, 2011, 32(3): 647-654 CAO Wen-gui, ZHAO Heng, ZHANG Yong-jie, et al. Strain Softening and Hardening Damage Constitutive Model for Rock Considering Effect of Volume Change and Its Parameters Determination Method[J]. Rock and Soil Mechanics, 2011, 32(3): 647-654 |
| [11] | 张嘎, 张建民. 粗粒土与结构接触面受载过程中的损伤[J]. 力学学报, 2004, 36(3): 322-327 ZHANG Ga, ZHANG Jian-min. Load-induced Damage of the Interface between Structure and Coarse Grained Soil[J]. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(3): 322-327 |
| [12] | 胡黎明, 濮家骝. 土与结构物接触面损伤本构模型[J]. 岩土力学, 2002, 23(1): 6-11 HU Li-ming, PU Jia-liu. Damage Model of Soil-structure Interface[J]. Rock and Soil Mechanics, 2002, 23(1): 6-11 |
| [13] | 李键. 粗糙度对粘性土-混凝土结构接触面力学特性的影响[D]. 长沙: 中南大学, 2014. LI Jian. Relationship between Roughness and Mechanical Properties of Clay-concrete Interface[D]. Changsha:Central South University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10533-1014398749.htm |
| [14] | 徐辉, 韩青锋, 连晓伟, 等. 黏性土固结不排水剪切的滑动损伤模型研究[J]. 岩土力学, 2008, 29(9): 2383-2386 XU Hui, HAN Qing-feng, LIAN Xiao-wei, et al. A Damage Constitutive Model for Clay Based on the Analysis of Sliding of Skeleton Grains[J]. Rock and Soil Mechanics, 2008, 29(9): 2383-2386 |
| [15] | 李新平, 陈俊桦, 李友华, 等. 溪洛渡电站地下厂房爆破损伤范围及判据研究[J]. 岩石力学与工程学报, 2010, 29(10): 2042-2049 LI Xin-ping, CHEN Jun-hua, LI You-hua, et al. Study of Criterion and Damage Zone Induced by Excavation Blasting of Underground Power-house of Xiluodu Hydropower Station[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 2042-2049 |
| [16] | 曹文贵, 赵明华, 刘成学. 基于Weibull分布的岩石损伤软化模型及其修正方法研究[J]. 岩石力学与工程学报, 2004, 23(19): 3226-3231 CAO Wen-gui, ZHAO Ming-hua, LIU Cheng-xue. Study on the Model and Its Modifying Method for Rock Softening and Damage Based on Weibull Random Distribution[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3226-3231 |
| [17] | 殷宗泽, 许国华. 土与混凝土接触面剪切特性[C]//第六届全国土力学及基础工程学术会议论文集. 上海: 同济大学出版社, 1991: 97-100. YIN Zong-ze, XU Guo-hua. Shear Properties of Soil and Concrete Interface[C]//The Sixth National Conference on Soil Mechanics and Foundation Engineering Academic. Shanghai: Tongji University Press, 1991:97-100. |
| [18] | DESAI C S, ZAMAN M M, LIGHTNER J G, et al. Thin Layer Element for Interfaces and Joints[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1984, 8(1): 19-43 |
| [19] | 殷宗泽, 朱泓, 许国华. 土与结构材料接触面的变形及其数学模拟[J]. 岩土工程学报, 1994, 16(3): 14-22 YIN Zong-ze, ZHU Hong, XU Guo-hua. Numerical Simulation of the Deformation in the Interface between Soil and Structural Material[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3): 14-22 |
 2017, Vol. 34
2017, Vol. 34
