扩展功能
文章信息
- 刘诗福, 凌建明, 袁捷, 杨文臣
- LIU Shi-fu, LING Jian-ming, YUAN Jie, YANG Wen-chen
- 基于竖向加速度响应的机场道面平整度评价及IRI标准反演
- Evaluation and IRI Criteria Inversion of Airport Pavement Roughness Based on Vertical Acceleration Response
- 公路交通科技, 2017, 34(5): 57-64
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(5): 57-64
- 10.3969/j.issn.1002-0268.2017.05.008
-
文章历史
- 收稿日期: 2016-06-18
2. 云南省交通规划设计研究院 陆地交通气象灾害防治技术国家工程试验室, 云南 昆明 650431
2. National Engineering Laboratory for Surface Transportation Weather Impacts Prevention, Yunnan Communications Planning and Design Institute, Kunming Yunnan 650431, China
当前,我国机场道面平整度评价主要沿用于高速公路评价标准体系[1-2],然而,飞机的胎压、起落架构型及荷载作用等特性与汽车存在较大差异[3]。为科学准确掌握道面的平整度的健康状态和提升机场道面的管理水平,亟需根据飞机及机场道面特性,制定科学的机场道面平整度评价标准。
国际上机场道面平整度的评价尚没有统一的标准及方法。美国联邦航空总局(FAA)和国际民航组织(ICAO)采用直尺检测法;波音公司根据飞机滑行的疲劳寿命建立了三级平整度评价标准[4];加拿大运输部提出了基于行驶舒适度(RCI)的评价方法;美国某工程咨询公司提出以驾驶员处和飞机重心处的加速度平方和根值作为评价指标。我国机场道面平整度的评价主要参考公路路面平整度的评价方法,采用国际平整度指数(IRI)进行评价[2]。IRI采用激光平整度仪快速准确测试,适用于机场停航时间短、道面检测相对频繁等要求。但是,源自高速公路的机场道面IRI的评价标准过度强调了机场道面与公路路面的共性,而忽略机场道面的特性。蔡婉彤、周晓青等利用ADAMS软件考查飞机在不平整道面滑行时的竖向加速度响应,以期反演机场道面的平整度评价标准[3, 5],但该软件自带的Aircraft模型(战斗机较多)不能有效表征市场上民用飞机的动力学响应。多数学者建立单自由度或双自由度的飞机动力学模型和振动方程,以理论解析飞机竖向加速度响应,虽然这类方法简单且易求解,但忽略飞机自身的转动而不能真实地模拟飞机运动状态[5-7]。同时,飞机起落架轮胎与地面的接触采用“点接触”模型[8-11],而没有考虑飞机轮胎的几何滤波效果[12]。
文中建立飞机整机的六自由度动力学模型及振动方程,选取最大竖向加速度响应作为机场道面平整度的评价指标并采用Simulink仿真模块进行快速求解,在不同平整度的道面激励和不同滑行速度条件下,综合分析飞机4个代表部位的最大竖向加速度值的分布规律,并根据波音公司疲劳标准,采用图解法反演得到机场道面平整度IRI评价的标准值。
1 飞机动力学建模 1.1 基本考虑(1) 竖向运动:飞机竖向运动视为一个含簧载质量和非簧载质量的振动系统[8-11]。簧载质量包括机身、机翼和缓冲器外筒质量;非簧载质量包括刹车装置、轮胎等质量,并将起落架的缓冲器和轮胎都视作含一定刚度系数的弹簧和一定阻尼系数的阻尼器并联而成。
(2) 俯仰转动:多数飞机动力学建模将簧载质量简化成一个位置固定的点质量[5-7],以建立单自由度或双自由度的数学模型。这忽略了飞机自身的俯仰转动,不能真实地反映其动力学响应。
(3) 侧倾转动:多数飞机动力学模型认为飞机的水平振动相对竖向振动较小而忽略侧倾转动[13],但事实上飞机主起落架和前起落架的横向距离大,跑道或滑行道的横向不均匀性使得两者受到的不平整激励并不一致,因而需考虑飞机的侧倾转动。
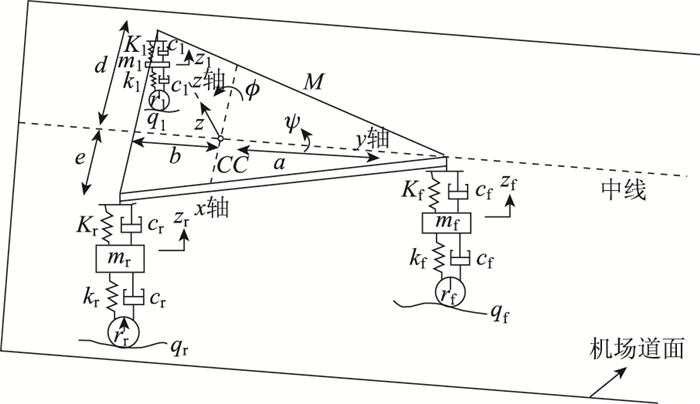
1.2 动力学模型根据飞机竖向运动、俯仰转动和侧倾转动的基本动力学性能,六自由度的飞机整机模型如图 1所示[8-10]。在竖向运动方面:M为飞机模型的簧载质量;mf,ml,mr分别为前、左后、右后起落架非簧载质量;Kf,Kl,Kr分别为前、左后、右后起落架簧载质量的刚度系数;Cf,Cl,Cr分别为前、左后、右后起落架簧载质量的阻尼系数;kf,kl,kr分别为前、左后、右后起落架非簧载质量的刚度系数;cf,cl,cr分别为前、左后、右后起落架非簧载质量的阻尼系数;rf,rl,rr分别为前、左后、右后起落架轮胎的半径;qf,ql,qr分别为前、左后、右后起落架非簧载质量受到的不平整道面激励;Z,zf,zl,zr分别为簧载质量、前、左后、右后起落架非簧载质量的竖向位移。在转动性能方面:Ix,Iy为飞机模型绕x轴、y轴的转动惯量,a,b分别为前后起落架到x轴的垂直距离,d,e分别为左后、右后起落架到y轴的垂直距离;Φ,Ψ为簧载质量的俯仰转动和侧倾转动位移。
|
| 图 1 六自由度的飞机整机动力学模型 Fig. 1 Aircraft kinetic model with 6-DOF |
| |
1.3 振动方程
在图 1中,飞机动力学模型通常沿y轴对称,左后起落架和右后起落架到y轴的垂直距离相等,即e=d。根据达朗贝尔原理,以飞机平衡位置为坐标原点,在不平整道面的激励下簧载质量M的竖向振动平衡方程[8-10]:
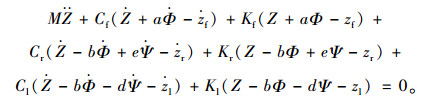
|
(1) |
簧载质量M的俯仰转动平衡方程:
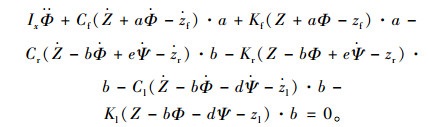
|
(2) |
簧载质量M的侧倾转动平衡方程:
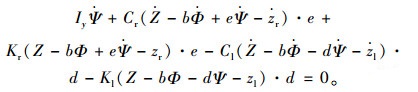
|
(3) |
前、左后、右后起落架的非簧载质量在竖直方向的平衡方程:
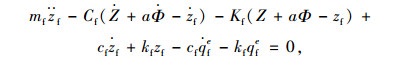
|
(4) |
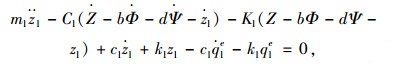
|
(5) |
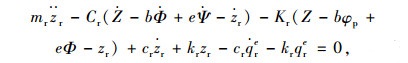
|
(6) |
式中,qfe,qle,qre分别为前、左后、右后起落架轮胎几何滤波后的有效路形。
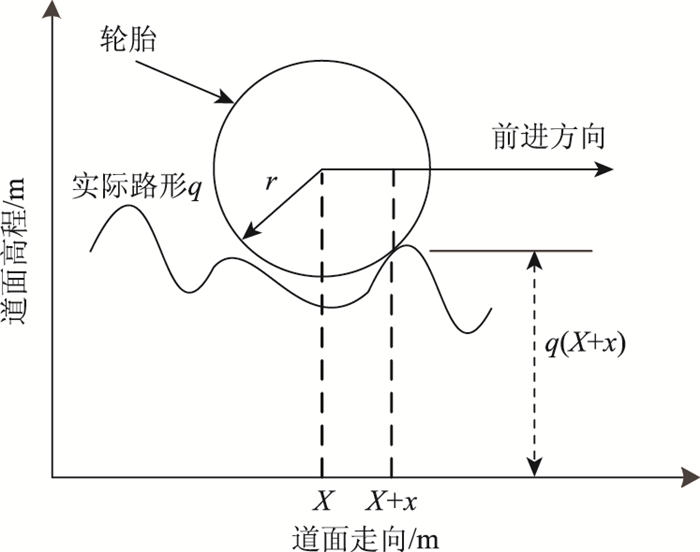
1.4 不平整道面的有效路形定义飞机滑行过程中实际测量的路面纵剖面不平度序列为实际路形q,而经过飞机轮胎包络滤波后的路形为有效路形qe。在式(4)~(6) 的飞机动力学模型中,可采用有效路形替代实际路形作为不平整激励输入,而由于轮胎是唯一获取道面激励的子系统,轮胎模型直接影响到有效路形,进而决定飞机振动模型的精度。轮胎与地面接触的模型通常包括“点接触”、“刚性滚子”和“弹性滚子”等模型[12]。“点接触”模型求解简单而应用广泛,但该模型不考虑轮胎的包络特性,不适合路面凸起的冲击振动。张韡等[11]通过实际试验分析结果表明当轮胎胎压较高(飞机胎压可达1.4 MPa)而变形较小时,简化的刚性轮胎更接近实测试验结果。据此,研究采用“刚性滚子”轮胎接触模型,如图 2所示。
|
| 图 2 “刚性滚子”模型轮胎的包络特性 Fig. 2 Envelope characteristics of rigid roller tire model |
| |
对“刚性滚子”轮胎,有效路形和实际路形的关系[14]:
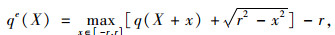
|
(7) |
式中,qe(X)为在X点处的有效路形;q(X)为X处的实际路形;r为飞机轮胎的半径。
2 竖向加速度评价指标及求解 2.1 竖向加速度评价指标机场道面的不平整会使飞机滑行时产生竖向加速度。既有研究表明竖向加速度与道面平整度的相关性最高,可综合表征飞机构件的疲劳损伤和乘客的不舒适性[15];当竖向加速度大于0.4g时乘客会感觉不舒适,同时飞机长期处于这种条件下会很快降低机身结构和跑道道面结构的疲劳寿命[3]。《人体暴露于全身振动的评价》表明人体的舒适性与承受的竖向加速度相关[16]。波音公司早期根据飞机的滑行疲劳试验,提出了基于竖向加速度的平整度三级(0.25g,0.55g和0.80g)评价标准[4]。美国某工程咨询公司根据代表机型的大量仿真结果,以驾驶员和飞机重心处0.4g竖向加速度为阈值,作为道面是否需要维修的判断准则。为综合分析飞机竖向和转向运动作用于机身不同部位的加速度响应激励的差异性,如图 3所示,研究选取飞机重心处、驾驶员、前舱位和后舱位4个代表部位的竖向加速度作为机场道面平整度的潜在评价指标,计算原理:

|
(8) |
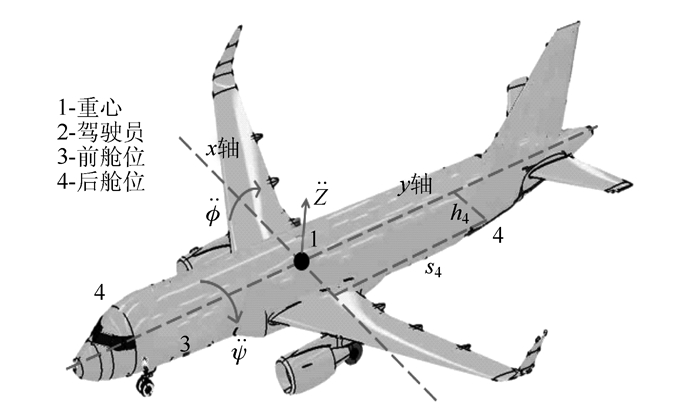
|
| 图 3 飞机代表部位的示意 Fig. 3 Schematic diagram of aircraft reprehensive parts |
| |
式中,ai为部位i的竖向加速度;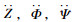
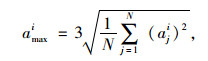
|
(9) |
式中,N为采集的点数,aji为飞机i部位的第j个样本点的竖向加速度数值。
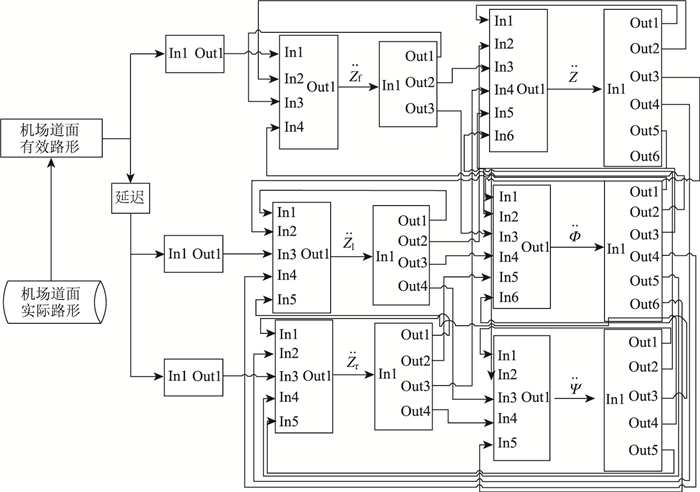
2.2 Simulink仿真求解求解式(1)~(6) 的振动平衡方程描述了六自由度飞机模型在不平整激励下的动力学响应,可采用解析法或数值法计算出飞机不同部位在不平整道面激励下的位移、速度和加速度等特征参数。然而,振动平衡方程的参数众多且各物理量存在耦合,解析解难以表达和计算。Simulink提供一个动态系统建模、仿真和综合分析的集成环境,具有仿真精细、效率高且灵活的优点。如图 4所示,为解析不同条件下飞机动力学响应的演化特性,研究采用Simulink建立飞机动力学系统仿真模型以进行快速地大量求解。Simulink建模主要步骤包括:(1) 根据仿真机型轮胎的半径等参数,根据式(7) 将机场道面实际路形转化为有效路形;(2) 确定整个系统的输入,包括有效路形、主起落架延迟时间等;(3) 建立6个加速度为核心的子系统,并根据式(1)~(6) 连接各子系统;(4) 在系统中配置代表机型的模型参数;(5) 根据飞机的滑行速度和道面长度确定仿真时间;(6) Simulink仿真并根据式(8) 和(9) 计算4个代表部位的最大竖向加速度,综合分析其仿真结果。
|
| 图 4 飞机动力学Simulink仿真模型 Fig. 4 Aircraft kinetics Simulink simulation model |
| |
2.3 IRI标准值的反演
对于某种代表机型而言,飞机各部位的竖向加速度响应除了与道面的不平整状态r有关,还取决于飞机的滑行速度v。因此,飞机各部位竖向加速度:
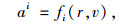
|
(10) |
式中,ai为部位i的竖向加速度;fi(·)为部位i竖向加速度的函数映射关系。机场道面平整度评价的主要对象是跑道和滑行道,记道面的代表滑行速度为v0,道面不平整状态r采用国际平整度指数IRI进行表征,l等级平整度下代表部位i对应的最大竖向加速度的分界阈值为[amini, amaxi],则l等级道面下IRI的分界阈值[m, n]可由式(10) 反算:
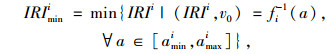
|
(11) |
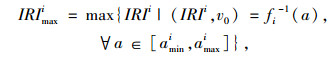
|
(12) |
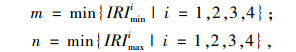
|
(13) |
式中,fi-1(·)为与fi(·)对应的反函数;根据波音公司疲劳标准[4],最大竖向加速度小于0.25g为新建道面标准,最大竖向加速度小于0.4g为旧道面标准[5]。为与现有《民用机场道面评价技术管理规范》中平整度评价分级“好、中、差”相对应[2],研究定义机场道面平整度分级标准如下:好(0~0.25g),中(0.25g~0.4g),差(>0.4g)。
3 实例应用 3.1 代表机型目前市场运营飞机的种类众多,分析机型不仅要具有代表性,还要能简化模型以提高计算效率。选取目前某C类主流客机为代表机型,该机型参数为:M=59 033 kg; mf=390 kg; ml=mr=888 kg; Kf=109 759 N/m; Kl=Kr=614 264 N/m; Cf=143 000 N/(m·s-1); Cl=Cr=625 000 N/(m·s-1); kf=kl=kr=4 000 000 N/m; Ix=2 442 187 kg·m2; Iy=1 342 834 kg·m2; cf=cl=cr=4 066 N/(m·s-1); a=11.86 m; b=0.78 m; d=3.8 m; e=3.8 m; rf=0.40 m; rr=rl=0.605 m。
3.2 机场道面激励若将道面视作连续曲面,则道面纵断面的平整度序列可视为一种随机现象,服从高斯概率分布的零均值各态历经随机场。采用功率谱密度函数可描述这种平稳遍历特性[5]。根据《车辆振动输入路面平度表示方法》[17],在空间频率n1 < n < n2条件下,道面功率谱Gq(n)采用式(13) 进行拟合计算:
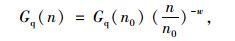
|
(14) |
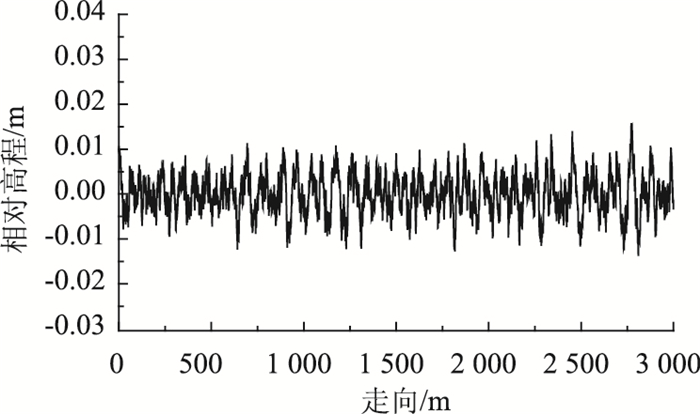
式中,Gq(n0)为路面不平度系数;n0为参考空间频率,取0.1 m-1;w为频率指数,取2。FAA研究成果表明:显著影响飞机的道面空间波长范围为0.5~120 m[18],即机场道面的空间频率分布范围为0.08 < n < 2。试验选取道面长度为3 000 m,相邻两采样点的水平距离为0.25 m [14]。通过控制不平度系数并采用谐波叠加法可生成不同平整度的随机道面[19]。其中A级道面(Gq(n0)取值为16×10-6m2/m-1)的纵断面随机场如图 5所示[17]。
|
| 图 5 A级道面纵断面的随机场 Fig. 5 Random field of A-graded pavement profile |
| |
3.3 试验设计
试验1:道面IRI的作用机理。控制飞机滑行速度不变,路面不平度系数取值为8×10-6~144×10-6 m2/m-1,步长为8×10-6m2/m-1,生成不同平整度的随机道面。试验方案中以仿真机型的前、左后和右后起落架受到的不平整激励的IRI平均值作为道面IRI值,解析代表机型在不同IRI值道面下的最大竖向加速度响应的差异。
试验2:飞机滑行速度的作用机理。控制路面不平度系数取值不变,在相同平整度道面下解析代表机型在不同滑行速度下的最大竖向加速度响应差异,飞机滑行速度取值为0~300 km/h,步长为10 km/h。
试验3:道面IRI及滑行速度的协同作用机理。在试验1及试验2的基础上,综合分析飞机最大竖向加速度响应在不同平整度纵断面(IRI)及滑行速度同时作用下的分布特性。
3.4 分析与讨论(1) 不同飞机部位
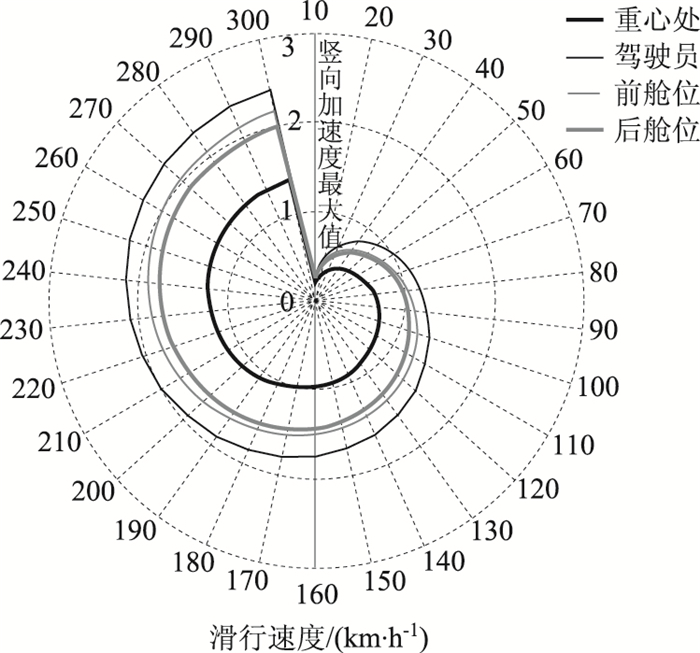
在A级道面下,4个代表部位的最大竖向加速度随滑行速度变化的分布如图 6所示。4个代表部位的竖向加速度均随着滑行速度的增加而增加,即飞机滑行速度越高,各代表部位的振动越剧烈。在相同的滑行速度下,最大竖向加速度从大到小排列依次为驾驶员、前舱位、后舱位和重心处,即当飞机在不平整道面上滑行时,对驾驶员造成的不舒适性最大,这将严重影响驾驶员对仪器表的读数。前舱位和后舱位的乘客感受到的振动相当,并且都比重心处的乘客更剧烈些。
|
| 图 6 不同飞机部位的最大竖向加速度特性 Fig. 6 Characteristics of maximum vertical acceleration of different aircraft parts |
| |
(2) 不同滑行速度及道面IRI值
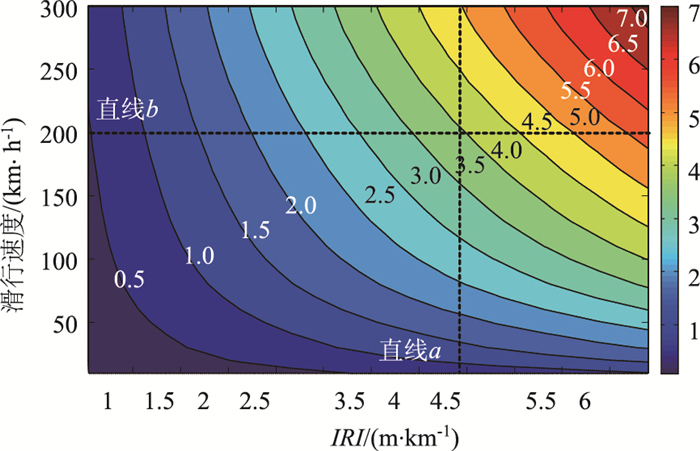
以最不利的驾驶员处为例,在不同道面平整度及滑行速度作用下最大竖向加速度的分布如图 7所示。最大竖向加速度随滑行速度和道面IRI值的增大而增大,等值线(虚曲线)整体上呈指数函数递减的特征,若要控制驾驶员处的最大竖向加速度处于同一水平,需降低飞机滑行速度或提高道面的IRI值。对同一水平IRI值(垂直直线a),图中相邻等值线相交的距离随着滑行速度的增加而增加,这表明最大竖向加速度与滑行速度之间呈非线性递增关系,且最大竖向加速度的梯度变化随滑行速度增加呈递减趋势。对同一水平滑行速度(水平直线b),图中相邻等值线相交的距离相等,IRI值对最大竖向加速度的影响呈线性递增的趋势。
|
| 图 7 不同道面IRI和滑行速度下驾驶员处最大竖向加速度分布 Fig. 7 Distribution of maximum vertical accelerations of driver with different IRI values and taxiing speeds on pavement |
| |
(3)IRI评价标准值的反演
① 最大竖向加速度的回归模型
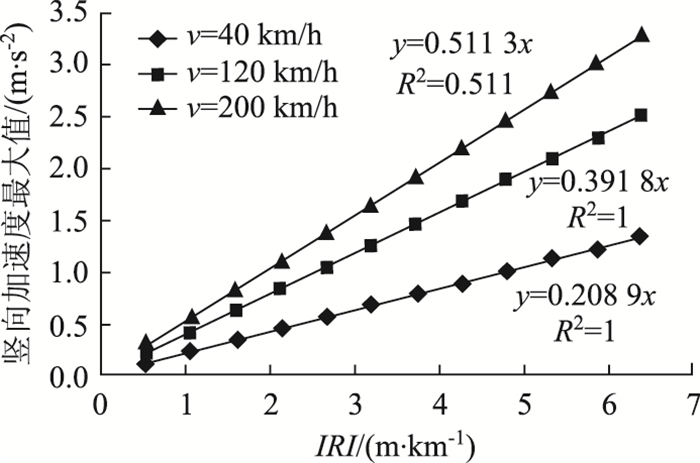
根据随机道面下Simulink的大量仿真结果,提取各代表部位的最大竖向加速度随滑行速度v和道面IRI值变化的有效样本。在滑行速度一定的情况下,采用SPSS软件的线性回归分析各代表部位的最大竖向加速度与道面IRI值关系,发现两者呈高度线性相关,见图 8,拟合R2均为1;而在道面IRI值一定的情况下,利用SPSS的曲线回归分析各代表部位的最大竖向加速度与滑行速度关系,发现两者呈幂函数高度相关,见图 9,拟合R2均大于0.99。最大竖向加速度的回归预测模型的通用解析式。
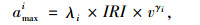
|
(15) |
|
| 图 8 重心处最大竖向加速度与道面IRI值关系 Fig. 8 Relationship between maximum vertical acceleration at centre of gravity and IRI of pavement |
| |
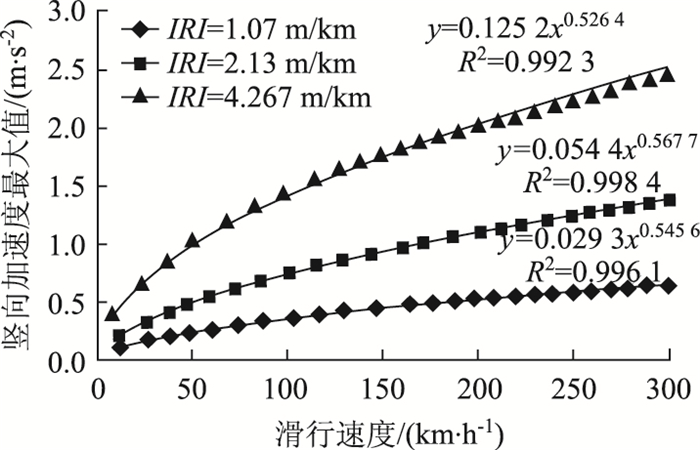
|
| 图 9 重心处最大竖向加速度与滑行速度的关系 Fig. 9 Relationship between maximum vertical acceleration at centre of gravity and taxiing speed |
| |
式中,i为部位的编号,i∈[1, 4];γi为速度修正系数;λi为比例系数。4个代表部位的回归预测模型分别为:
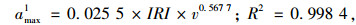
|
(16) |
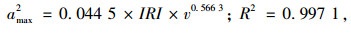
|
(17) |
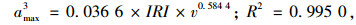
|
(18) |
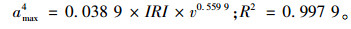
|
(19) |
模型拟合的R2表明:4个预测模型的拟合度好,模型较可靠。各部位的γi值不同但差异不大,均分布在0.55~0.6之间;各部位的λi差异明显,决定最大竖向加速度的放大倍数,且λ2>λ4>λ3>λ1,即驾驶员处的比例系数最大而重心处最小,这与图 6中不同位置最大竖向加速度的分布特性相吻合。
② IRI标准值反演
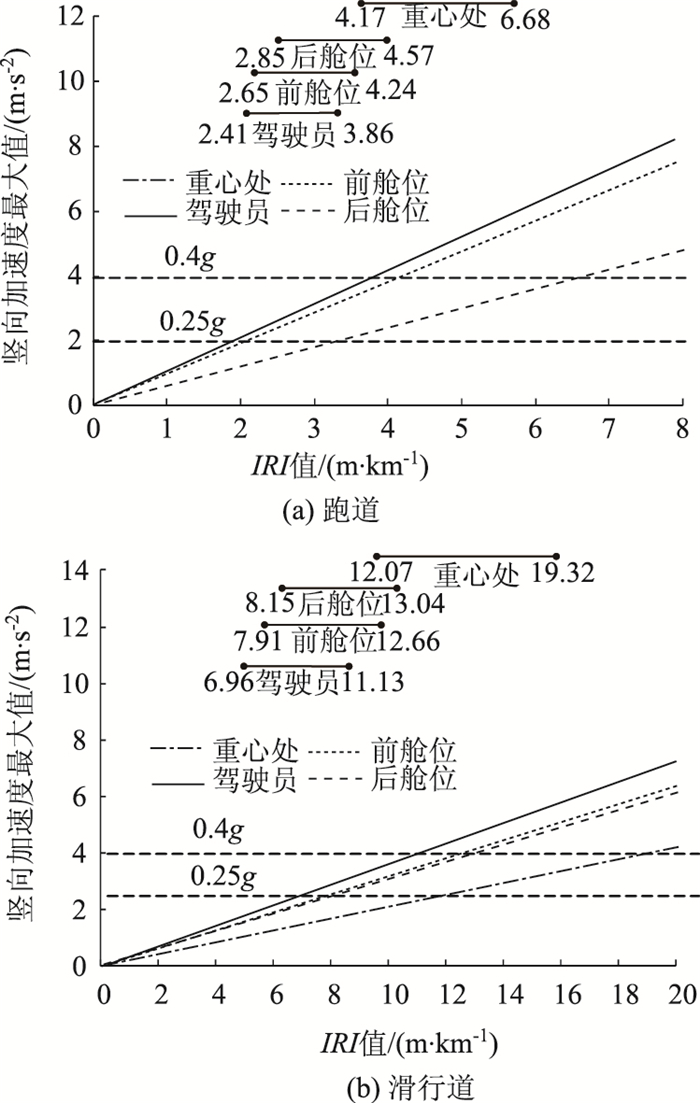
飞机在滑行道上一般以20~40 km/h的速度滑行,而C类飞机的进近速度为121~140 knots,研究先取40 km/h作为滑行道的代表速度;140 knots(约260 km/h)作为跑道的代表速度。根据式(15)~(18),4个代表部位的最大竖向加速度与IRI值的分布关系如图 10所示。根据2.3中基于最大竖向加速度的机场道面平整度的分级阈值标准,各部位IRI标准值反演的示意如图 10中水平短线所示。
|
| 图 10 机场道面平整度评价的IRI值反演 Fig. 10 Inversion of IRI value for airport pavement roughness evaluation |
| |
现有机场道面评价标准的IRI值[3]和本研究反演的IRI值比较如表 1所示。研究提出的平整度评价方法及反演的标准值严格区分了跑道和滑行道,与现有标准相比,反演的IRI标准值更为宽松,且跑道的平整度标准比滑行道更严格。这与实际中具有不同滑行速度的机场道面的平整度分布特征相吻合。
| 评价等级 | 好 | 中 | 差 | |
| 跑道/ (m·km-1) | 现有标准值 | < 2.0 | 2.0~4.0 | >4.0 |
| 反演值 | < 2.4 | 2.4~3.9 | >3.9 | |
| 滑行道/ (m·km-1) | 现有标准值 | < 2.0 | 2.0~4.0 | >4.0 |
| 反演值 | < 7.0 | 7.0~11.1 | >11.1 | |
4 结论
(1) 综合考虑飞机的竖向运动、俯仰和侧倾转动,建立了不平整道面激励下六自由度的飞机整机动力学模型及相应的振动方程,采用“刚性滚子”轮胎接触模型有效表征飞机轮胎的几何滤波效应,并利用Matlab/Simulink仿真模块进行快速求解。以飞机代表部位的最大竖向加速度作为平整度的评价指标,提出机场道面IRI值反演的数学表达。
(2) 飞机各部位的最大竖向加速度与道面的IRI值和滑行速度相关,随道面IRI值线性增加,而随滑行速度非线性增加,变化梯度随滑行速度的增加而减小。飞机在不平整道面滑跑过程中,驾驶员处于最不利状态。
(3) 在服从高斯分布的随机道面激励下,建立了最大竖向加速度与道面和滑行速度之间的数学回归预测模型,并基于波音疲劳标准,反演机场道面评价的IRI标准值。与既有标准值相比,反演的IRI值可区分跑道和滑行道;且跑道的IRI标准值比滑行道更为严格。
(4) 研究成果可为机场道面平整度评价标准的修订提供一种参考方法,并抽取机场道面管理的重要特征参数。但受限于试验条件,研究采用随机道面激励及单一代表机型,未来将开展机场道面现场的实测观察以及多种机型仿真,进一步验证和优化研究发现。
| [1] | JTG F40—2004, 公路沥青路面施工技术规范[S]. JTG F40—2004, Technical Specification for Construction of Highway Asphalt Pavements[S]. |
| [2] | MH/T 5024—2009, 民用机场道面评价技术管理规范[S]. MH/T 5024—2009, Technical Specifications of Aerodrome Pavement Evaluation and Management[S]. |
| [3] | 蔡宛彤, 种小雷, 王海服, 等. 基于ADAMS的机场道面平整度评价方法[J]. 空军工程大学学报:自然科学版, 2014, 15(1): 15-19 CAI Wan-tong, CHONG Xiao-lei, WANG Hai-fu, et al. An Evaluation Method for Roughness of Airport Pavement Based on ADAMS[J]. Journal of Air Force Engineering University: Natural Science Edition, 2014, 15(1): 15-19 |
| [4] | DEBORD K J. Runway Roughness Measurement, Quantification and Application: The Boeing Approach[R]. Washington, D.C.: Boeing Commercial Airplane Group Airport Technology Organization, 1995. |
| [5] | 周晓青. 机场道面平整度评价指标研究[D]. 上海: 同济大学, 2006. ZHOU Xiao-qing. Study on Airport Pavement Roughness Evaluation Indexes[D]. Shanghai: Tongji University, 2006. |
| [6] | 赵磊, 李光元, 史保华, 等. 公路飞机跑道道面凹形变坡动力分析[J]. 长安大学学报:自然科学版, 2010, 30(2): 44-47 ZHAO Lei, LI Guang-yuan, SHI Bao-hua, et al. Dynamic Analysis on Concave Grade Turn Point of Highway Runway Pavement Used by Aircraft[J]. Journal of Chang'an University: Natural Science Edition, 2010, 30(2): 44-47 |
| [7] | 程国勇, 侯栋文, 黄旭栋. 基于动荷载系数限值的道面平整度分析技术[J]. 中国民航大学学报, 2016, 34(4): 59-64 CHENG Guo-yong, HOU Dong-wen, HUANG Xu-dong. Analysing Technology of Pavement Roughness Based on Dynamic Load Factor Limits[J]. Journal of Civil Aviation University of China, 2016, 34(4): 59-64 |
| [8] | SIVAKUMAR S, HARAN A P. Mathematical Model and Vibration Analysis of Aircraft with Active Landing Gears[J]. Journal of Vibration and Control, 2015, 21(2): 229-245 |
| [9] | GHARAPURKAR A, JAHROMI A F, BHAT R B, et al. Semi-active Control of Aircraft Landing Gear System Using H-infinity Control Approach[C]//2013 International Conference on Connected Vehicles and Expo (ICCVE). Las Vegas: World Academy of Connected Vehicles, 2013: 679-686. |
| [10] | TOLOEI A, AGHAMIRBAHA E, ZARCHI M. Mathematical Model and Vibration Analysis of Aircraft with Active Landing Gear System Using Linear Quadratic Regulator Technique[J]. International Journal of Engineering-Transactions B: Applications, 2016, 29(2): 137-144 |
| [11] | 程国勇, 郭稳厚. 基于多自由度飞机模型的机场道面平整度评价方法[J]. 南京航空航天大学学报, 2016, 48(4): 606-614 CHENG Guo-yong, GUO Wen-hou. Airport Pavement Roughness Evaluation Based on Three-degree-of-freedom Aircraft Model[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(4): 606-614 |
| [12] | 郭孔辉, 刘青, 丁国峰. 轮胎包容特性分析及其在汽车振动系统建模中的应用[J]. 汽车工程, 1999, 21(2): 65-71, 80 GUO Kong-hui, LIU Qing, DING Guo-feng. Analysis of Tire Enveloping Properties and its Application in Modeling of Vehicle Vibration Systems[J]. Automotive Engineering, 1999, 21(2): 65-71, 80 |
| [13] | 邓松武. 跑道平整度及道面破损对飞机运行的影响研究[D]. 天津: 中国民用航空大学, 2006. DENG Song-wu. Effects of Runway Roughness and Pavement Distress on Aircraft Operations [D].Tianjin: Civil Aviation University of China, 2006. |
| [14] | 张韡, 魏朗, 余强. 基于有效路形的车辆振动模型[J]. 交通运输工程学报, 2008, 8(4): 16-19, 24 ZHANG Wei, WEI Lang, YU Qiang. Vehicle Vibration Model Based on Effective Road Profiles[J]. Journal of Traffic and Transportation Engineering, 2008, 8(4): 16-19, 24 |
| [15] | ZHANG H, YANG W. Evaluation Method of Pavement Roughness Based on Human-vehicle-road Interaction[C]//The 10th International Conference of Chinese Transportation Professionals. Beijing: American Society of Civil Engineers, 2010: 3541-3551. |
| [16] | BS ISO2631—1: 1997, Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—General Requirements[S]. |
| [17] | GB7031—86, 车辆振动输入路面平度表示方法[S]. GB7031—86, Vehicle Vibration—Describing Method for Road Surface Irregularity[S]. |
| [18] | FAA. Guidelines and Procedures for Measuring Airfield Pavement Roughness[R]. Washinton, D.C.: U.S. Department of Transportation, 2009. |
| [19] | 聂彦鑫, 李孟良, 过学迅, 等. 基于谐波叠加法的路面不平度重构[J]. 汽车科技, 2009, 37(4): 55-58 NIE Yan-xin, LI Meng-liang, GUO Xue-xun, et al. Road Roughness Simulation Based on Partial Wave Adding Model[J]. Automobile Science & Technology, 2009, 37(4): 55-58 |
 2017, Vol. 34
2017, Vol. 34
