扩展功能
文章信息
- 张艳红, 申爱琴, 侯芸
- ZHANG Yan-hong, SHEN Ai-qin, HOU Yun
- 柔性路面结构层模量梯度控制与论证
- Control and Verification of Modulus Gradient of Flexible Pavement Structural Layers
- 公路交通科技, 2017, 34(5): 28-34
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(5): 28-34
- 10.3969/j.issn.1002-0268.2017.05.004
-
文章历史
- 收稿日期: 2016-07-28
2. 中国公路工程咨询集团有限公司, 北京 100093;
3. 中国交建公路路面养护技术研发中心, 北京 100093
2. China Highway Engineering Consulting Group Co., Ltd., Beijing 100093, China;
3. Research and Development Center on Highway Pavement Maintenance Technology, CCCC, Beijing 100093, China
半刚性基层沥青路面在我国高等级公路中应用广泛,然而,半刚性路面不可避免的反射裂缝及造成路面早期破坏严重的问题也日益突出[1]。近年来,以柔性材料为基层的柔性基层沥青路面在很多地区得到越来越多的研究及应用。其中,沥青稳定碎石与级配碎石为当前正在逐步探索实践的柔性基层材料。路面结构优化设计是柔性路面应用中至关重要的一步,即通过优化各结构层的设计组合实现力学响应的合理分布。具体来讲,通过合理设计保证相邻结构层刚度适中,从而实现各结构层受力平衡。一般来讲,由于柔性基层模量与面层模量相差较大,因而基层与面层之间刚度变化过于突兀,导致层间受力较不利。目前国内柔性路面研究尚属于起步阶段,在理论分析和实体工程方面积累了一些经验和成果[2-4],但以结构层模量控制为主导的研究基本尚属空白。鉴于此,文中以采用沥青稳定碎石及级配碎石为柔性路面的结构层模量比进行研究,采取Bisar3.0全面计算基层及面层模量比变化时结构受力情况,并以广州某实体工程为依托进行性能验证,据此为优化柔性基层沥青路面的推广应用提供依据。
1 计算说明 1.1 结构层模量梯度控制理论在路面总体结构层设置上,为了保证结构的受力均衡,一般要求相邻结构层之间的刚度不宜迥异过大。当相邻层的相对刚度比过大时,上层底面将产生较大的弯拉应力或弯拉应变。当弯拉应力或应变值超过材料强度或应变极限时,上层便产生开裂[2]。
对于采用沥青稳定碎石+级配碎石的柔性基层沥青路面,由于级配碎石的模量较低,这种结构组合将使路面结构呈现沥青稳定碎石高模量、级配碎石基层低模量的刚度组合,使二者之间界面承受较大的弯拉响应,造成结构受力不利。因此,对柔性路面而言,控制结构层的模量梯度在合理范围内对结构受力优化较为重要。
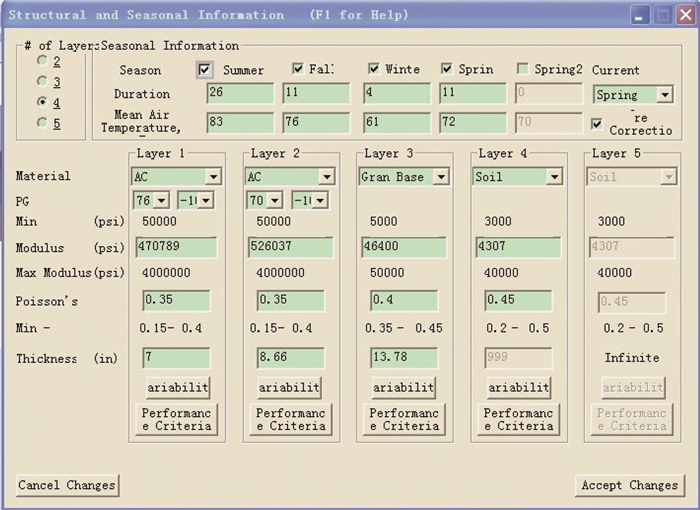
1.2 路面结构方案采用美国PerRoad 3.5软件经温度修正优化后的动态模量作为参数, 如图 1所示。泊松比主要参照美国SHRP计划中长期路面项目中推荐值,且级配碎石与土基均按较不利条件取值。计算时考虑基层厚度及模量比变化的影响,即选取3个厚度水平、4个模量水平下进行分析。选取典型柔性路面方案及材料参数见表 1[5-6]。
|
| 图 1 PerRoad 3.5优化界面 Fig. 1 Optimized interface of PerRoad 3.5 |
| |
| 材料名称 | 厚度/cm | 动态弹模量/MPa | 泊松比 |
| AC | 18 | 2 730 | 0.35 |
| ATB | 22 | 3 086 | 0.35 |
| 级配碎石 | 30/40/50 | 385/308/257/220 | 0.40 |
| 未筛分碎石 | 15 | 180 | 0.40 |
| 土基 | - | 80 | 0.45 |
1.3 计算说明 1.3.1 车轮荷载
文中的计算荷载采用标准轴载100 kN,胎压与轮载半径均参照现行规范取值[5]。
1.3.2 层间条件文中考虑两种不完全连续。其具体条件如下[1]:
(1) 沥青层各层之间完全连续;
(2) 沥青层与级配碎石层按滑动计算。
2 柔性路面在不同模量比下的力学响应计算与分析结合研究需要,考虑8,10,12及14等4个模量比条件下柔性路面的力学响应。文中所述的模量比指的是ATB层与级配碎石的模量之比,也称为模量梯度比。
2.1 面层最大弯拉应变面层的拉应变是国外沥青路面的常用设计指标,以此控制沥青层疲劳开裂。本研究选取面层的最大拉应变作为比选标准之一,对比面层的弯拉水平高低。具体结果见表 2。
| 模量比 | 级配碎石厚度(cm)的最大弯拉应变/με | ||
| 30 | 40 | 50 | |
| 8 | 81.1 | 78.6 | 76.4 |
| 10 | 82.1 | 80.1 | 78.2 |
| 12 | 82.8 | 81.2 | 79.7 |
| 14 | 83.4 | 82.1 | 80.8 |
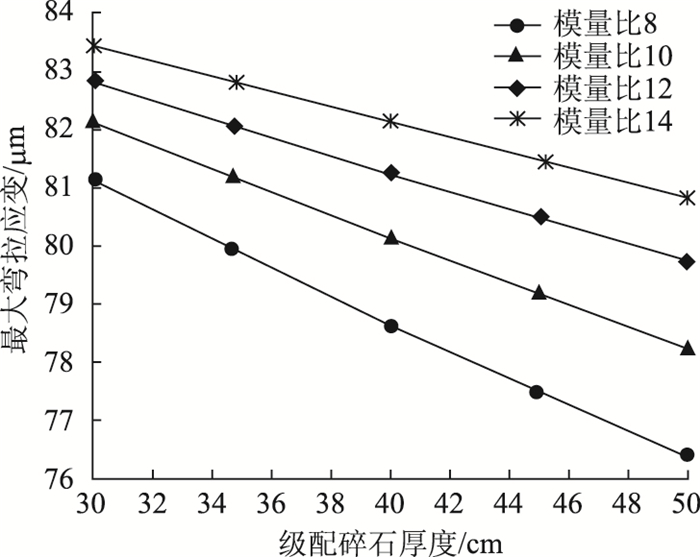
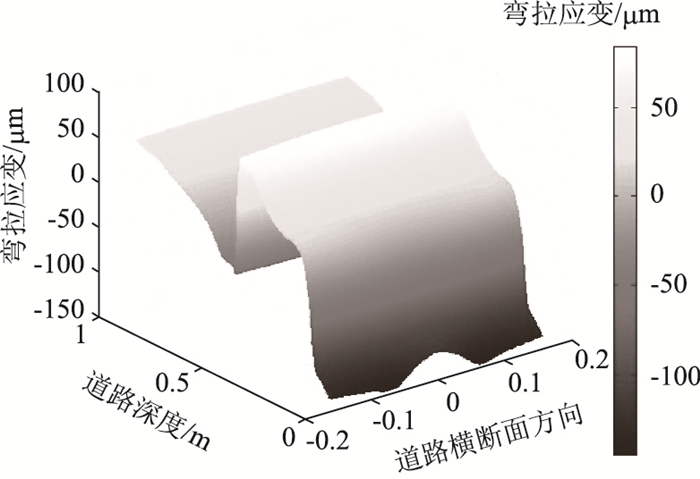
4个模量比条件下柔性路面的基层厚度与结构最大弯拉应变的关系图见图 2。弯拉应变在道路空间范围的三维分布见图 3。
|
| 图 2 面层最大拉应变与模量比关系图 Fig. 2 Relationa between surface maximum tensile strain and modulus ratio for surface layer |
| |
|
| 图 3 柔性路面弯拉应变三维分布代表图 Fig. 3 Representative 3D distribution of flexible strain of flexible pavement |
| |
(1) 计算知,在层间不完全连续条件下,结构的最大弯拉应变均出现于关键层位(沥青稳定碎石与级配碎石接触界面)单圆荷载中心处,这与弯拉应力的极值点位置相同。
(2) 在不同的模量梯度比下,结构最大弯拉应变随级配碎石基层厚度的增大而减小。在同一基层厚度条件下,随着模量比从8增大到14,结构的弯拉应变随之增大。因此,较大的级配碎石模量及刚度有利于使柔性路面结构保持较低的基层弯拉应变水平,从而有利于提高结构的疲劳寿命。
(3)4个模量比条件下柔性路面的弯拉应变三维分布较为相似:从路表起往下,弯拉应变迅速增大,并在沥青稳定碎石层深度范围内(9~11 cm)实现弯拉应变的拉压转换,随后逐渐增大,直至达到沥青稳定碎石层底实现了结构的弯拉应变峰值。随后,从级配碎石往下,应变骤变为受压,并随深度延深而呈一定幅度的递增。
2.2 结构最大弯拉应力层底弯拉应力为我国现行规范的设计指标。本研究特选取结构的最大弯拉应力进行比选,对比结构的弯拉水平,结果见表 3。
| 模量比 | 级配碎石厚度(cm)的结构最大弯拉应力/MPa | ||
| 30 | 40 | 50 | |
| 8 | 0.303 3 | 0.292 3 | 0.282 3 |
| 10 | 0.308 | 0.299 1 | 0.291 1 |
| 12 | 0.311 6 | 0.304 3 | 0.297 7 |
| 14 | 0.314 5 | 0.308 5 | 0.303 |
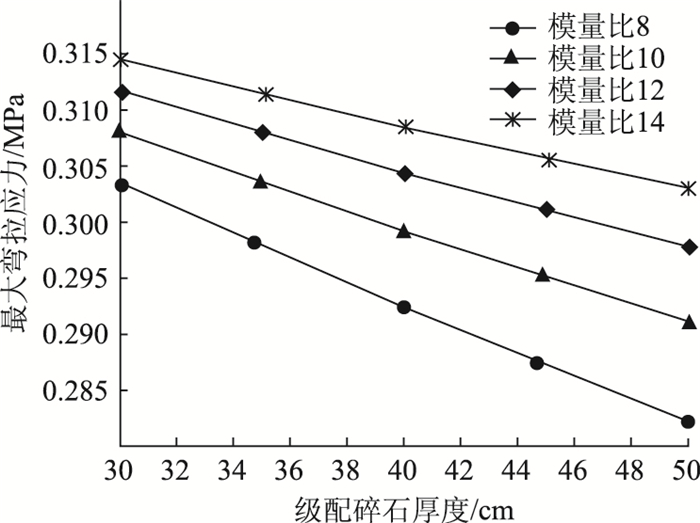
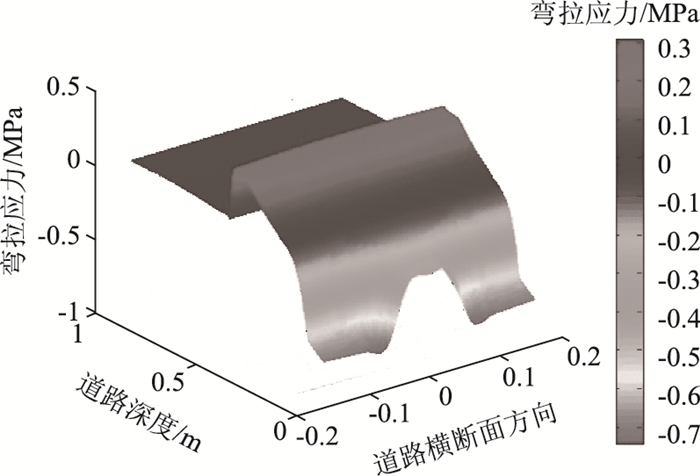
4个模量比条件下柔性路面的基层厚度与结构最大弯拉应力的关系图见图 4。弯拉应力在道路空间范围的三维分布见图 5。
|
| 图 4 结构最大拉应力与模量比关系图 Fig. 4 Relations between structural maximum tensile stress and modulus ratio |
| |
|
| 图 5 柔性路面弯拉应力三维分布代表图 Fig. 5 Representative 3D distribution of flexible stress of flexible pavement |
| |
(1) 在层间不完全连续条件下,柔性结构的最大弯拉应力均出现于关键层位(沥青稳定碎石与级配碎石接触界面)单圆荷载中心处。
(2) 由图 4可知,在不同的模量梯度比下,结构最大弯拉应力均随级配碎石基层厚度的增大而减小,这与弯拉应变的变化规律相似。此外,模量比越小,结构弯拉应力越小。这是由于模量比越小,级配碎石的模量则越大,较大的模量有利于抵御层间的弯拉应力。从控制结构弯拉应力及弯拉应变的角度,级配碎石与面层的模量比应取低值。
(3)4个模量比条件下柔性路面的弯拉应力三维分布总体上相似:从路表起往下,弯拉应力迅速增大,并在沥青稳定碎石层深度范围内(17~19 cm)实现弯拉应力的拉压转换,随后逐渐增大,直至达到沥青稳定碎石层底实现了结构的弯拉应力峰值。随后,从级配碎石往下,应力骤变为受压,并随深度延深而呈小幅度递增。
2.3 面层最大剪应力控制结构剪应力水平是路面抗剪设计的重点[7]。结构主要受剪部位通常在于中上面层。本研究选取面层最大剪应力指标进行比较,反映模量比在剪应力控制下的合理范围。具体结果见表 4。
| 模量比 | 级配碎石厚度(cm)面层最大剪应力/MPa | ||
| 30 | 40 | 50 | |
| 8 | 0.204 7 | 0.206 9 | 0.209 1 |
| 10 | 0.203 9 | 0.205 7 | 0.207 4 |
| 12 | 0.203 3 | 0.204 8 | 0.206 2 |
| 14 | 0.202 8 | 0.204 | 0.205 2 |
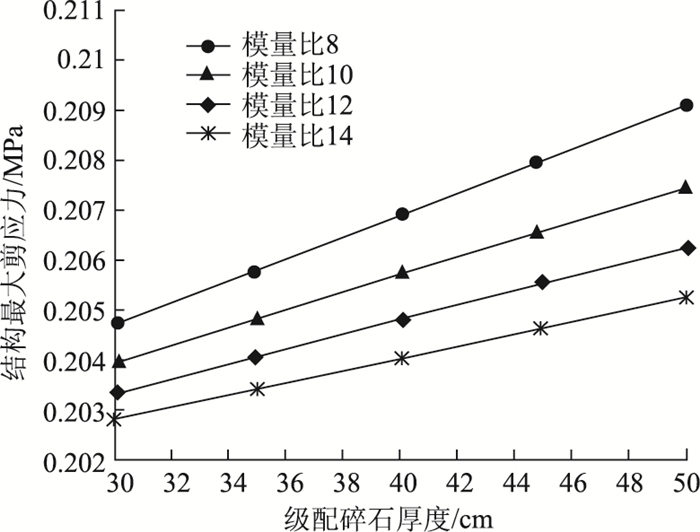
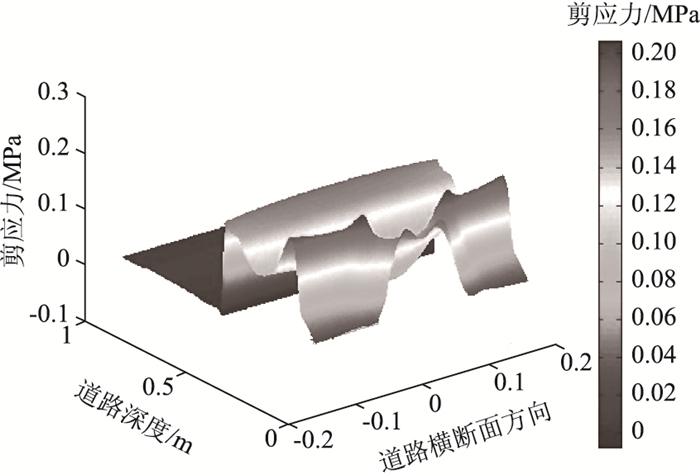
4个模量比条件下柔性路面的基层厚度与结构最大剪应力的关系图见图 6。剪应力在道路空间范围的三维分布见图 7。
|
| 图 6 面层最大剪应力与级配碎石厚度关系图 Fig. 6 Relations between surface maximum shear stress and graded gravel thickness |
| |
|
| 图 7 柔性路面剪应力三维分布代表图 Fig. 7 Representative 3D distribution of shear stress of flexible pavement |
| |
(1) 计算知,路面结构最大剪应力均出现在距路表 0.02 m深,距轮隙中心0.64 m处。距路表 0.02 m均为大部分结构的受剪高峰区域。参照现行《城镇道路路面设计规范》(CJJ 169—2011)[7],其中规定:沥青面层剪应力最大值计算点位置应取荷载外边缘路表距单圆荷载中心点0.9R点D或离路表 0.1h1距单圆荷载中心点E(h1为上面层厚度,R为荷载半径0.106 5 m)。其中E点的点位与本文计算的结果较为相近,即在荷载中心半径范围内,与路表极为接近处,即上面层范围内偏中上层位的深度处。
(2) 由图 7可知,在各个模量梯度比下,结构最大剪应力随级配碎石厚度增大而增大。当模量比增大,面层最大剪应力减小。可见较大的模量比对控制结构剪应力水平较为有利。从结构抗剪的角度讲,模量比不宜取过低值。
(3)4个模量比条件下柔性路面的剪应力三维分布总体上较为相似:从路表起往下,剪应力迅速增大,直至达到面层范围内剪应力峰值;随后剪应力随深度延深而递减。加密计算结果显示,当深度大于10 cm时,剪应力即处于相对较低的应力水平。在沥青稳定碎石层范围内,两类结构的剪应力均呈先减小后增大的变化趋势。随后达级配碎石层顶面,剪应力迅速骤减,在图 7中显示为曲面的急剧跌落。随后在基层范围内,剪应力处于较低水平并呈缓和增长。
2.4 结构模量比推荐综合以上力学分析知,对于采用“ATB+级配碎石”为基层的柔性基层沥青路面而言,随着模量梯度比的增加,结构的最大弯拉响应逐渐增大,同时面层最大剪应力随之减小。当模量梯度比在8~10,即级配碎石模量在300~400 MPa时,结构的受力状况分析如下:
(1) 弯拉响应:结构的整体弯拉水平较低,且最大弯拉应力与最大弯拉应变均出现于关键层位(沥青稳定碎石与级配碎石接触界面)单圆荷载中心处。参考国内相关科研单位的研究成果[9-18],柔性路面中,沥青混合料疲劳极限应变范围为70~80 με。当模量比为8~10时,层间不连续条件下的结构最大弯拉应变可满足疲劳极限要求,与柔性路面自上而下非结构性破坏的受力模式相吻合。
(2) 剪应力:面层最大剪应力水平较高,最大剪应力位于上面层范围内偏中上层位的深度处。对比各个模量梯度下的水平,剪应力随级配碎石模量变化的总体幅度不大。因此,级配碎石模量变化对面层剪应力影响不是很大。为了提高路面的抗剪能力,建议加强上面层的抗车辙性材料设计。
综上,对于采用级配碎石的柔性基层沥青路面,通过对结构弯拉应力与剪应力水平实行双控,控制级配基层模量在合理范围内取相对高限值,能有效控制结构受力均衡。建议控制柔性基层与面层的模量比为8~10。
3 柔性路面长期性能为了验证柔性路面的工程性,以广州某高速公路为依托,选取如表 5所示两种结构铺设(结构B为半刚性基层路面结构),并于试验路完工后及通车3 a后监测路面的性能。
| 结构A | 结构B |
| 4 cm GAK-13A | 4 cm GAK-13A |
| 6 cm AC-20C | 6 cm AC-20C |
| 8 cm AC-25C | 8 cm AC-25C |
| 22 cm ATB-25 | 18 cm水稳碎石 |
| 45 cm级配碎石 | 18 cm水稳碎石 |
| 20 cm水稳碎石 | |
| 15 cm未筛分碎石 | 26 cm未筛分碎石 |
3.1 基于FWD及CBR检测的模量梯度反算
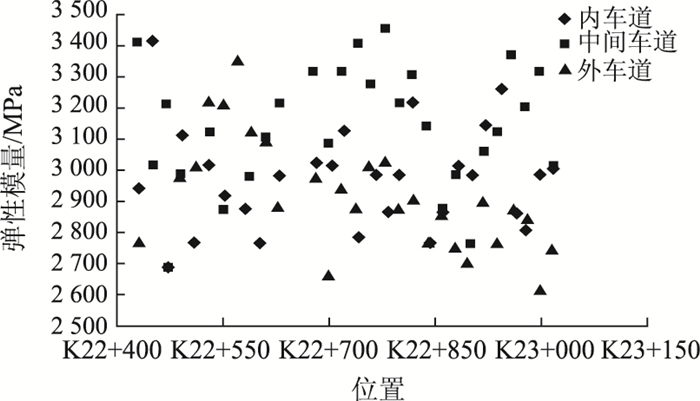
在试验路施工完工后,分别在面层及基层施工后选择3个车道进行FWD弯沉检测,试验结果见表 6。FWD模量反算的分布见图 8。
| ATB反算模量/ MPa | 桩号 | CBR/% | 级配碎石 模量/MPa | 面基层模量比 | ||
| 内侧车道 | 2 936 | K23+720外 | 117 | 371.25 | 内侧车道 | 7.87 |
| 中间车道 | 3 115 | K23+800外 | 117 | 371.25 | 中间车道 | 8.35 |
| 外侧车道 | 2 814 | K23+960外 | 117 | 371.25 | 外侧车道 | 7.99 |
| K24+040中 | 118 | 373.27 | ||||
| K24+140内 | 118 | 373.27 | ||||
| K24+240外 | 82 | 295.71 | ||||
| 平均值 | 2 955 | 111.5 | 359.33 | 8.07 | ||
|
| 图 8 ATB模量反算分布图 Fig. 8 Distribution of back-calculated ATB modulus for ATB |
| |
在级配碎石基层施工后进行CBR检测,按照美国AASHTO推荐的换算关系式将CBR值反算为回弹模量值Mr。
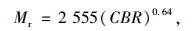
|
(1) |
式中,Mr为回弹模量值,1 psi=145 MPa;CBR为加州承载比。
经现场检测可知,试验路各个车道的模量梯度比在7.87~8.35之间,模量梯度均值为8.07,基本满足结构优化中模量梯度比为8~10的要求。
3.2 长期性能监测为了验证柔性基层沥青路面在广东地区的适用性,试验段通车后的4 a时间里,连年监测路面的各项性能,检测结果见表 7。
| 结构 | 指标 | 2009.12 | 2010.11 | 2011.11 | 2012.11 |
| 结构 A | 100 m路面损坏状况指数 | 98.8 | 96.3 | 94.5 | 91.2 |
| 100 m车辙指数 | 98.7 | 98.5 | 99.6 | 98.4 | |
| 100 m平整度 | 93.7 | 94.6 | 95.1 | 94.4 | |
| 最大弯沉(0.01 mm) | 12.15 | 11.98 | 12.78 | 13.65 | |
| 结构 B | 100 m路面损坏状况指数 | 99.0 | 95.3 | 91.2 | 86.1 |
| 100 m车辙指数 | 99 | 98.9 | 98.9 | 98.8 | |
| 100 m平整度 | 93.6 | 93.8 | 93.5 | 92.7 | |
| 最大弯沉(0.01 mm) | 8.87 | 7.62 | 9.61 | 14.53 |
(1) 通车4 a后,由于基层反射裂缝的出现,半刚性基层试验段B的路况等级降为良;柔性基层试验段A路况等级全为优。
(2) 通过FWD动态弯沉检测知,就承载能力而言,柔性基层试验段的弯沉集中在10~20(0.01 mm)的区间内,远小于路面设计所要求的容许最大弯沉0.44 mm。半刚性结构的总体弯沉虽然在通车前几年较小,但后期由于基层模量的衰变等原因导致弯沉骤增。
(3) 试验段各年的车辙指数均为优。柔性基层试验段在2009~2010年间车辙量平均增长了0.5 mm,而半刚性结构则在2008~2009年间平均增长了约1 mm的车辙量。柔性基层试验段的车辙指数并不亚于半刚性结构。
(4) 两种结构平整度指数均为优,且随着使用年数的增加,平整度指数变化不大。
4 结论本文考查了在层间不连续条件下,结构层模量梯度控制中的重要指标-ATB与级配碎石层模量比、基层厚度对柔性路面力学响应的影响,得出以下结论:
(1) 在层间不完全连续条件下,结构的最大弯拉应力及最大弯拉应变位于关键层位(沥青稳定碎石与级配碎石接触界面)单圆荷载中心处。
(2) 在不同的模量梯度比下,结构最大弯拉应变及弯拉应力均随级配碎石基层厚度的增大而减小。在同一基层厚度条件下,随着模量比从8增大到14,结构的弯拉应变随之增大。因此,较大的级配碎石模量及刚度有利于使柔性路面结构保持较低的基层弯拉应变水平,从而有利于提高结构的疲劳寿命。
(3) 结构最大剪应力位于上面层中部。在各个模量梯度比下,结构最大剪应力随级配碎石厚度增大而增大。随着模量比的增大,面层的最大剪应力随之减小。
(4) 通过对柔性结构的弯拉应力与剪应力水平实行双控,控制基层模量在合理范围内取相对高限值,能有效控制受力均衡。建议控制基层与面层的模量比为8~10。
(5) 以广州某高速公路为依托,通过在施工后对基面层模量进行检测及连续4 a长期性能的观测,印证了在“ATB+级配碎石”为柔性基层的结构中,采用8~10的结构层模量梯度有利于控制柔性路面性能保持在较优的水平。
| [1] | 沈金安, 李福普, 陈景. 高速公路沥青路面早期损坏分析与防治对策[M]. 北京: 人民交通出版社, 2004. SHEN Jin-an, LI Fu-pu, CHEN Jing. Analysis and Preventive Techniques of Premature Damage of Asphalt Pavement in Expressway[M]. Beijing: China Communications Press, 2004. |
| [2] | 王端宜. 设计沥青路面及其方法的研究[D]. 广州: 华南理工大学, 2003. WANG Duan-yi. Study of Design and Method of Asphalt Pavement[D]. Guangzhou: South China University of Technology, 2003. |
| [3] | 崔华杰, 李立寒, 刘栋. 高模量沥青混凝土低温抗裂性能研究[J]. 公路交通科技, 2014, 31(2): 38-41 CUI Hua-jie, LI Li-han, LIU Dong. Research on Low-temperature Anti-crack Performance of High Modulus Asphalt Mixture[J]. Journal of Highway and Transportation Research and Development, 2014, 31(2): 38-41 |
| [4] | 黄晓明, 范要武, 赵永利, 等. 高速公路沥青路面高温车辙的调查与试验分析[J]. 公路交通科技, 2007, 24(5): 16-20 HUANG Xiao-ming, FAN Yao-wu, ZHAO Yong-li, et al. Investigation and Test of Expressway Asphalt Pavement High-temperature Performance[J]. Journal of Highway and Transportation Research and Development, 2007, 24(5): 16-20 |
| [5] | JTG D50—2006, 公路沥青路面设计规范[S]. JTG D50—2006, Specifications for Design of Highway Asphalt Pavement[S]. |
| [6] | 张静, 魏连雨, 马士宾, 等. 动载作用下半刚性基层沥青路面动力响应现场测试及数值模拟[J]. 公路交通科技, 2016, 33(10): 19-24 ZHANG Jing, WEI Lian-yu, MA Shi-bin, et al. Field Test and Numerical Simulation of Dynamic Response of Semi-rigid Base Asphalt Pavement under Moving Vehicle Load[J]. Journal of Highway and Transportation Research and Development, 2016, 33(10): 19-24 |
| [7] | CJJ 169—2011, 城镇道路路面设计规范[S]. CJJ 169—2011, Code for Pavement Design of Urban Road [S]. |
| [8] | 张睿. 柔性路面在非破坏性检测中的力学性质研究[D]. 兰州: 兰州大学, 2015. ZHANG Rui. Study on Mechanical Properties of Flexible Pavement in the Non-destructive Testing[D]. Lanzhou:Lanzhou University, 2015. |
| [9] | 李鹏. 长寿命沥青路面设计指标研究[D]. 西安: 长安大学, 2007. LI Peng. Study on Indexes for Perpetual Asphalt Pavement Design[D]. Xi'an: Chang'an University, 2007. |
| [10] | 董旭鹏. 基于材料非线性的多轴重载下沥青路面结构响应分析[D]. 南京: 东南大学, 2015. DONG Xu-peng. Analysis of Asphalt Pavement Response under Multi Axle Load Based on Material Nonlinearity[D]. Nanjing:Southeast University, 2015. |
| [11] | 平树江, 申爱琴, 李鹏. 长寿命路面沥青混合料疲劳极限研究[J]. 中国公路学报, 2009, 22(1): 34-38 PING Shu-jiang, SHEN Ai-qin, LI Peng. Study of Fatigue Limit of Asphalt Mixture for Perpetual Pavement[J]. China Journal of Highway and Transport, 2009, 22(1): 34-38 |
| [12] | 蔡旭, 王端宜, 吴旷怀, 等. 采用简化的分级掺配法设计抗车辙型沥青混合料[J]. 公路交通科技, 2016, 33(3): 13-17 CAI Xu, WANG Duan-yi, WU Kuang-huai, et al. Design of Rut Resistance Asphalt Mixture with Simplified Multilevel Mixing Method[J]. Journal of Highway and Transportation Research and Development, 2016, 33(3): 13-17 |
| [13] | 凌建明, 官盛飞, 赵鸿铎, 等. 公路沥青路面预养护多层次模型决策模型[J]. 公路交通科技, 2008, 25(6): 26-29 LING Jian-ming, GUAN Sheng-fei, ZHAO Hong-duo, et al. Multi-hierarchy Fuzzy Decision-making Model for PPM Treatment Selection of Highway Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development, 2008, 25(6): 26-29 |
| [14] | 冯德成, 胡伟超, 于飞, 等. 沥青路面材料热物性参数对温度场的影响及敏感性分析[J]. 公路交通科技, 2011, 28(11): 12-19 FENG De-cheng, HU Wei-chao, YU Fei, et al. Impact of Asphalt Pavement Thermophysical Property on Temperature Field and Sensitivity Analysis[J]. Journal of Highway and Transportation Research and Development, 2011, 28(11): 12-19 |
| [15] | 柳浩, 谭忆秋, 宋宪辉, 等. 沥青路面基-面层间结合状态对路面应力响应的影响分析[J]. 公路交通科技, 2009, 26(3): 1-6 LIU Hao, TAN Yi-qiu, SONG Xian-hui, et al. Influence of Bonding Condition Between Base and Surface Courses of Asphalt Pavement on Pavement Stress Response[J]. Journal of Highway and Transportation Research and Development, 2009, 26(3): 1-6 |
| [16] | 王旭东. 沥青路面弯沉指标的探讨[J]. 公路交通科技, 2015, 32(1): 1-12 WANG Xu-dong. Discussion of Asphalt Pavement Deflection Indicator[J]. Journal of Highway and Transportation Research and Development, 2015, 32(1): 1-12 |
| [17] | 王修山, 丁小军, 谢永利. 柔性路面粒料层的永久变形计算[J]. 上海交通大学学报, 2011, 45(5): 659-661 WANG Xiu-shan, DING Xiao-jun, XIE Yong-li. Permanent Deformation Computation Research of Graded Gravel Base in Flexible Pavement[J]. Journal of Shanghai Jiaotong University, 2011, 45(5): 659-661 |
| [18] | 白琦峰, 钱振东, 吴春颖. 基于实测验证的沥青路面力学模型研究[J]. 公路交通科技, 2011, 28(5): 39-41 BAI Qi-feng, QIAN Zhen-dong, WU Chun-ying. Study on Asphalt Pavement Mechanical Model Based on Calibration of Measurement[J]. Journal of Highway and Transportation Research and Development, 2011, 28(5): 39-41 |
 2017, Vol. 34
2017, Vol. 34
