扩展功能
文章信息
- 华艳秋, 郭晓晓, 张亮修, 吴光强
- HUA Yan-qiu, GUO Xiao-xiao, ZHANG Liang-xiu, WU Guang-qiang
- 汽车空气悬架非线性混沌分析
- Chaos Analysis on Nonlinearity of Vehicle Air Suspension
- 公路交通科技, 2017, 34(4): 123-129
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(4): 123-129
- 10.3969/j.issn.1002-0268.2017.04.018
-
文章历史
- 收稿日期: 2016-03-08
2. 上海市高级技工学校, 上海 200437;
3. 同济大学 汽车学院, 上海 201804
2. Shanghai Technician School, Shanghai 200437, China;
3. School of Automotive Studies, Tongji University, Shanghai 201804, China
近年来,非线性系统的混沌现象越来越受到人们的关注。汽车空气悬架具有复杂的非线性特性,其非线性因素在一定的载荷、激励和频域内表现十分突出,不容忽视。同时,悬架的各个子系统之间相互作用,其隔振系统的输出状态更容易进入混沌状态。因此有必要对非线性悬架的混沌运动进行研究,为汽车的动态设计和结构改进提供理论指导。
目前在非线性悬架建模、动态特性分析方面已有研究[1-2],并提出了有关混沌的控制和应用方法[3-4]。在汽车非线性悬架的混沌研究方面取得一定成果,但是对悬架的非线性主要是位移与速度的三次方来模拟[5-6]。Malin Presthus等[7]提出了轨道机车空气弹簧悬架的几种力学和数学模型,并研究了悬架参数对系统动力学特性的影响。Toyofuku Katuya等[8]研究了带附加气室的空气弹簧特性。A. Murata等[9]对单自由度膜式空气弹簧悬架系统的强迫振动进行了研究,通过理论计算和试验得到膜式空气弹簧的静态刚度和动态刚度,分析了其非线性恢复力,利用突破理论解释了系统分岔现象。文献[10]分析了连续减速带路面激励下的汽车悬架混沌的动力学行为,并进行混沌抑制。文献[11]研究了具有迟滞非线性特性的单自由度悬架模型在随机激励下的混沌运动。文献[12]考虑了汽车运行中重力项的影响,采用Melnikov函数研究了
本文基于所建立的汽车非线性空气弹簧悬架模型,建立二自由度悬架系统的动力学方程,在路面单频正弦激励情形下,研究悬架的系统响应,分析悬架非线性系统中的分岔以及混沌现象。
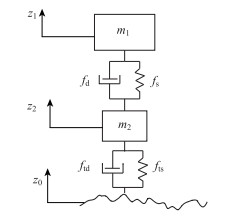
1 非线性悬架动力学模型 1.1 二自由度汽车垂向动力学建模如图 1所示为二自由度汽车垂向振动模型[13],其中m1为车身质量,m2为车轮质量,fs为悬架等效弹簧力,fd为悬架等效阻尼力,fts为轮胎等效弹簧力,ftd为轮胎等效阻尼力,z1为车身垂直位移,z2为车轮垂向位移,z0为路面激励位移。
|
| 图 1 二自由度汽车垂向振动模型 Fig. 1 Automobile vertical vibration model of two degrees of freedom |
| |
根据牛顿第二定律,得到二自由度汽车垂向运动微分方程:
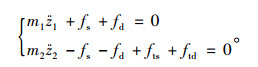
|
(1) |
为准确描述空气弹簧的非线性弹簧力与相对位移的关系,在某SUV汽车空气弹簧动刚度试验基础上,拟合得到不同气压下空气弹簧动刚度特性,进而完成空气弹簧非线性刚度建模。
试验方法为:将空气弹簧调至标准高度,按照压力从0.8 MPa (1 Bar=0.1 MPa) 到0.4 MPa,并且间减量为0.1 MPa的方式充入压缩空气。在每种气压下断开气源,以±50 mm的振幅和0.4 Hz的频率进行垂向振动10个循环,连续记录最后一个循环的弹簧力-位移特性曲线作为空气弹簧动刚度特性曲线。本试验为近似的绝热过程,其中弹簧力-位移曲线的斜率可以看作刚度值。
采用三次多项式对其非线性刚度特性进行拟合,得到不考虑迟滞特性下拟合空气弹簧非线性力-位移特性关系式为:
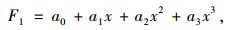
|
(2) |
式中, a0, a1, a2, a3为拟合系数; x为空气弹簧位移。
利用迹法模型对空气弹簧的迟滞特性进行拟合,描述空气弹簧的迟滞特性,其关系式为:
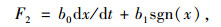
|
(3) |
式中, b0, b1为拟合系数;dx/dt为空气弹簧位移对时间t的导数。
联合式 (2)~(3) 得到考虑空气弹簧迟滞特性的弹簧力-位移特性为:
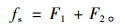
|
(4) |
用最小二乘法拟合得到多项式的各个系数,如表 1所示。
| 气压/MPa | a0 | a1 | a2 | a3 | b0 | b1 |
| 0.4 | 4 280.2 | 18.9 | 0.130 | 0.004 | 33.1 | 32.3 |
| 0.5 | 5 390.3 | 22.6 | 0.121 | 0.005 | 52.2 | 22.1 |
| 0.6 | 6 493 | 26 | 0.128 | 0.005 | 58 | 37.7 |
| 0.7 | 7 597.6 | 29.8 | 0.123 | 0.005 | 68.8 | 34.1 |
| 0.8 | 8 637.2 | 32.9 | 0.100 | 0.005 | 77.9 | 19.3 |
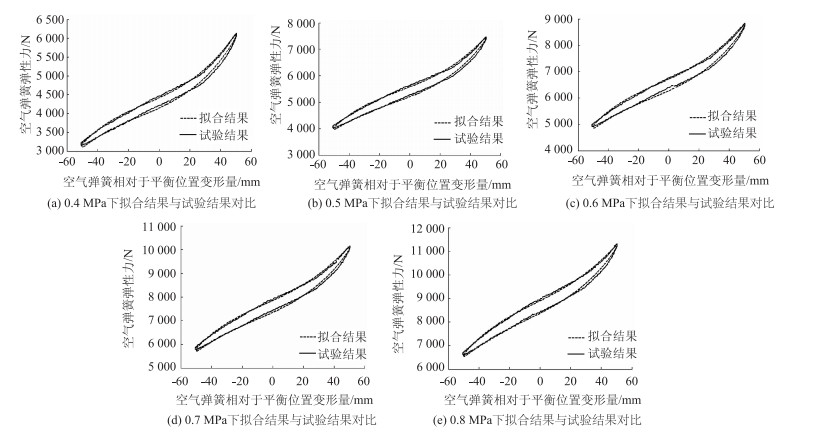
如图 2所示为不同气压下空气弹簧动刚度试验结果与数据拟合结果对比。
|
| 图 2 空气弹簧动刚度试验与拟合对比 Fig. 2 Comparison of air spring dynamic stiffness between test and fitting |
| |
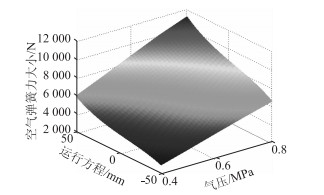
可以看出,采用拟合公式能比较准确描述空气弹簧的迟滞非线性特性,能满足空气弹簧非线性动力学分析需要。实际车辆工作过程中的弹簧气压是连续变化的,采用插值方法拟合得到连续气压变化下的空气弹簧特性,如图 3所示。
|
| 图 3 空气弹簧非线性特性三维拟合结果 Fig. 3 Three-dimensional fitting result of nonlinear characteristics of air spring |
| |
结合图 3空气弹簧特性和迟滞特性,完成空气弹簧的迟滞非线性动力学建模,该非线性模型基于试验结果,拟合精度较高,并且当车辆载荷不同时,空气弹簧刚度特性能随之体现,更加符合实际,能比较准确反映汽车的实际特性,可用于后文空气弹簧车辆动力学研究。
1.3 轮胎的非线性特性建模轮胎结构复杂且主要由橡胶元件组成,其非线性不可避免。将轮胎的弹性力和阻尼力分别看作是轮胎变形和变形速率的多项式函数,即:
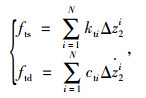
|
(5) |
式中,kti为轮胎刚度系数;cti为轮胎阻尼力系数;Δz2=z2-z0;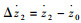
式 (5) 中的N值可以通过试验确定,有研究通过动态条件下轮胎弹性力和阻尼力变化试验得出N值取3[14],并指出:在试验结果中,各工况下轮胎弹性力系数kt1和kt2都不为0,95%的工况下kt3都为0;各工况下轮胎阻尼力系数ct1值都不为0,97%的工况下ct2和ct3都为0。因此,轮胎的弹性力和阻尼力可以足够精确地表示为:
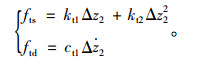
|
(6) |
另外,减振器的非线性阻尼特性用车身与车轮相对速度的二次多项式表示:
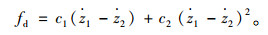
|
(7) |
将式 (2)~(7) 代入式 (1) 得到汽车二自由度垂向非线性系统动力学模型,参数见表 2。
| 参数名称 | 参数值 |
| 车身质量m1/kg | 842.75 |
| 非簧载质量m2/kg | 55 |
| 轮胎弹簧刚度kt1/(N·m-1) | 98 000 |
| 轮胎弹簧刚度kt2/(N·m-1) | 1 850 000 |
| 轮胎阻尼系数ct1/[(N·s·m)-1] | 3 012 |
| 悬架阻尼系数c1/[(N·s·m)-1] | 1 385.4 |
| 悬架阻尼系数c2/[(N·s·m)-1] | 524.28 |
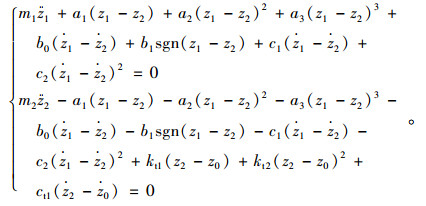
|
(8) |
大多数随机激励可以看作是很多个正弦函数叠加,为研究汽车空气悬架非线性分岔和混沌现象产生机理,这里路面激励为正弦激励,即:
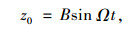
|
(9) |
式中,B为激励幅值; Ω为激励圆频率。
2 系统分岔及混沌数值仿真 2.1 系统混沌判断条件本文利用Matlab对所建立的悬架系统进行数值仿真,综合以下几个方面来研究二自由度悬架系统是否产生混沌现象。
(1) 系统的相轨迹[15], 通过数值计算,观察系统的相图结构。
(2) 庞加莱截面[16], 通过观察庞加莱截面上截点的情况判断是否发生混沌。当截面上有且只有一个不动点或少数离散点时,运动是周期的;当截面上是一封闭曲线时,运动是准周期的;当截面上是一些成分的具有分形结构的密集点时,运动便是混沌的。
(3) 李雅普诺夫指数[17], 从李雅普诺夫指数是否大于0判断。一个正的李雅普诺夫指数,意味着在系统相空间中,无论初始条件两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致无法预测,此即混沌现象。
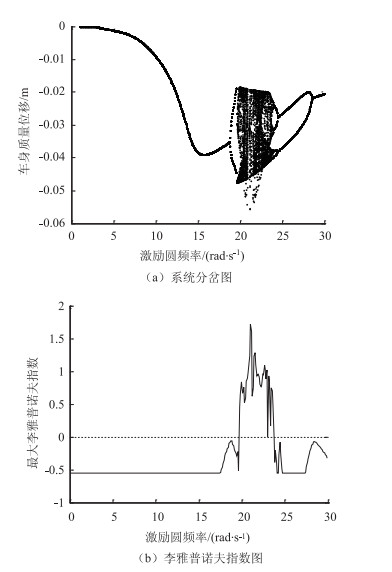
2.2 系统分叉数值仿真路面为单频正弦激励输入,取激励幅值B=0.024 5 m,以激励圆频率Ω为分岔参数,激励频率从0~30 rad/s变化,采用四阶定步长龙格-库塔方法进行数值积分,由于篇幅有限,本文只对车身质量位移非线性进行分析,车身质量位移分岔图以及李雅普诺夫指数图见图 4。
|
| 图 4 系统分岔与李雅普诺夫指数图 Fig. 4 System bifurcation and Lyapunov exponents diagram |
| |
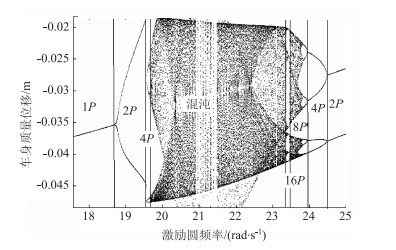
当李雅普诺夫指数为负或零时,系统处于周期或者拟周期运动;而当李雅普诺夫指数为正时,系统为混沌运动。结合分岔图以及李雅普诺夫指数图,可以看出,系统大约在20~24 rad/s之间出现混沌运动,由此进一步在此区间内计算系统的分岔图如图 5所示。
|
| 图 5 系统激励频率为18~25 rad/s时分岔图 Fig. 5 Bifurcation diagram when system excitation frequencies are 18-25 rad/s |
| |
在图 5中,P表示周期运动,1P表示周期一运动,2nP(n=1, 2, …, n) 表示周期2n运动。此外,从图 5还可以观察到,系统在发生分岔现象时表现为叉形分岔,这种周期加倍的分岔就是典型的倍周期分岔,倍周期分岔是系统从有序通往混沌的道路之一[18]。
2.3 系统混沌数值仿真下面取不同激励圆频率来分别计算系统的相图、庞加莱截面以及对应最大李雅普诺夫指数,分析系统的混沌现象。
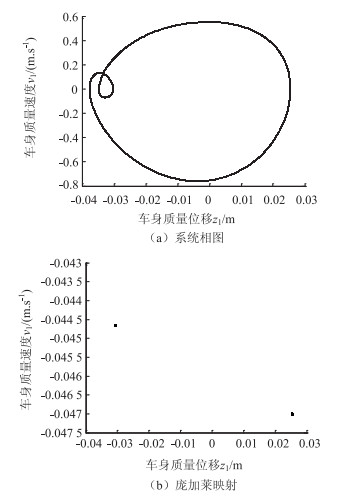
从图 6~10可以看出,系统在激励频率不同时呈现不同的稳定性特性。Ω为19 rad/s时由庞加莱映射以及最大李雅普诺夫指数可知,系统作稳定2周期运动;Ω为19.6 rad/s时,系统作4周期运动;Ω为20 rad/s和22 rad/s时,系统相图杂乱无章,最大李雅普诺夫指数为正,故此时系统为混沌;Ω为25 rad/s时,系统退化为2周期运动。表 3列出了不同激励圆频率下的最大李雅普诺夫指数。
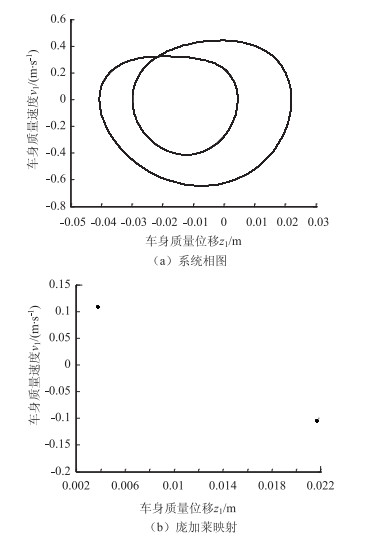
|
| 图 6 Ω为19 rad/s时系统相图和庞加莱映射 Fig. 6 Phase diagram and Poincaré mapping for Ω is 19 rad/s |
| |
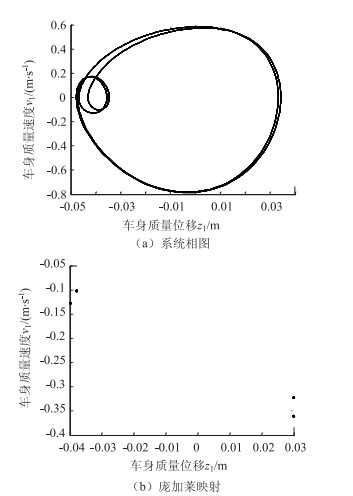
|
| 图 7 Ω为19.6 rad/s时系统相图和庞加莱映射 Fig. 7 Phase diagram and Poincaré mapping for Ω is 19.6 rad/s |
| |
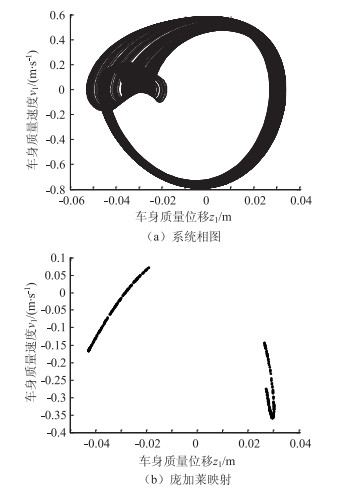
|
| 图 8 Ω为20 rad/s时系统相图和庞加莱映射 Fig. 8 Phase diagram and Poincaré mapping for Ω is 20 rad/s |
| |
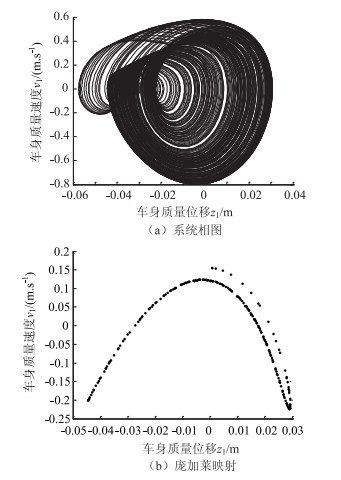
|
| 图 9 Ω为22 rad/s时系统相图和庞加莱映射 Fig. 9 Phase diagram and Poincaré mapping for Ω is 22 rad/s |
| |
|
| 图 10 Ω为25 rad/s时系统相图和庞加莱映射 Fig. 10 Phase diagram and Poincaré mapping for Ω is 25 rad/s |
| |
| 激励频率Ω/(rad·s-1) | 最大李雅普诺夫指数 |
| 19 | 0 |
| 19.6 | 0 |
| 20 | 0.542 |
| 22 | 1.1 |
| 25 | 0 |
3 结论
(1) 基于实测试验数据,拟合出考虑迟滞特性的空气弹簧非线性模型,通过与试验结果对比验证所建立模型的可行性。
(2) 二自由度系统在发生分岔现象时表现为叉形分岔,这种周期加倍的分岔就是典型的倍周期分岔,倍周期分岔是系统从有序通往混沌的道路之一。
(3) 单频正弦激励下系统的相轨迹、庞加莱映射以及李雅普诺夫指数图,证实了二自由度汽车非线性悬架系统中存在混沌现象。
| [1] | CUI Y, KURFESS T, MESSMAN M. A Methodology to Integrate a Nonlinear Shock Absorber Dynamics into a Vehicle Model for System Identification[J]. SAE International Journal of Materials & Manufacturing, 2011, 4(1): 527-534 |
| [2] | LEE K. Numerical Modelling for the Hydraulic Performance Prediction of Automotive Monotube Dampers[J]. Vehicle System Dynamics, 1997, 28(1): 25-39 |
| [3] | ANDRIEVSKII B R, FRADKOV A L. Control of Chaos: Methods and Applications in Mechanics[J]. Automation and Remote Control, 2003, 29(5): 33-56 |
| [4] | YASSEN M T. Chaos Control of Chaotic Dynamical Systems Using Backstepping Design[J]. Chaos Solitons & Fractals, 2006, 27(2): 537-548 |
| [5] | FU X L, DENG J, YANG J P. Bifurcations of Resonant Solutions and Chaos in Physical Pendulum Equation with Suspension Axis Vibrations[J]. Acta Mathematicae Applicatae Sinica, 2010, 26(4): 677-704 |
| [6] | 牛治东, 吴光强. 有界噪声激励下汽车悬架迟滞非线性系统的响应[J]. 同济大学学报:自然科学版, 2015, 43(10): 1557-1561 NIU Zhi-dong, WU Guang-qiang. Response of Hysteretic Nonlinear System of Vehicle Suspension Subjected to Bounded Noise Excitation[J]. Journal of Tongji University:Natural Science Edition, 2015, 43(10): 1557-1561 |
| [7] | MALIN PRESTHUS. Derivation of Air Spring Model Parameters for Train Simulation [D]. Lulea: Lulea University of Technology, 2002. |
| [8] | TOYOFUKU K, YAMADA C, KAGAWA T, et al. Study on Dynamic Characteristic Analysis of Air Spring with Auxiliary Chamber[J]. JSAE Review, 1999, 20(3): 349-355 |
| [9] | MURATA A, KUME Y, HASHIMOTO F. Application of Catastrophe Theory of Forced Vibration of a Diaphragm Air Spring[J]. Journal of Sound and Vibration, 1987, 112(1): 31-44 |
| [10] | 郑剑, 梁山, 朱勤, 等. 路面连续减速带下汽车悬架的混沌振动分析[J]. 公路交通科技, 2011, 28(1): 132-137 ZHENG Jian, LIANG Shan, ZHU Qin, et al. Chaotic Vibration of Vehicle Suspension Excited by Consecutive Speed Control Hump[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 132-137 |
| [11] | 牛治东, 吴光强. 随机激励下汽车非线性悬架系统的混沌研究[J]. 振动与冲击, 2016, 35(17): 39-43 NIU Zhi-dong, WU Guang-qiang. Chaos of a Vehicle Nonlinear Suspension System under Stochastic Excitation[J]. Journal of Vibration and Shock, 2016, 35(17): 39-43 |
| [12] | LITAK G, BOROWIEC M. Nonlinear Vibration of a Quarter-car Model Excited by the Road Surface Profile[J]. Communications in Nonlinear Science & Numerical Simulation, 2008, 13(7): 1373-1383 |
| [13] | 吴光强. 汽车理论[M]. 北京: 人民交通出版社, 2014. WU Guang-qiang. Automotive Theory[M]. Beijing: China Communications Press, 2014. |
| [14] | 高芳. 空气弹簧动态刚度和阻尼数学模型的建立[J]. 郑州轻工业学院学报:自然科学版, 2015, 30(增2): 103-107 GAO Fang. Mathematical Model Establishment for Dynamic Stiffness and Damp of Air Spring[J]. Journal of Zhengzhou University of Light Industry : Natural Science Edition, 2015, 30(3/4): 103-107 |
| [15] | 刘延柱, 陈立群. 非线性振动[M]. 北京: 高等教育出版社, 2001. LIU Yan-zhu, CHEN Li-qun. Nonlinear Vibration[M]. Beijing: Higher Education Press, 2001. |
| [16] | BHAUMIK I. Symbolic Dynamics and Chaos[M]. Munich: VDM Verlag Dr. Müller, 2011. |
| [17] | WOLF A, SWIFT J B, SWINNEY H L, et al. Determining Lyapunov Exponents From a Time Series[J]. Physica D: Nonlinear Phenomena, 1985, 16(3): 285-317 |
| [18] | 刘秉正, 彭建武. 非线性动力学[M]. 北京: 高等教育出版社, 2003. LIU Bing-zheng, PENG Jian-wu. Non-linear Dynamics[M]. Beijing: Higher Education Press, 2003. |
 2017, Vol. 34
2017, Vol. 34
