扩展功能
文章信息
- 潘兵宏, 苗慕楠, 张锟
- PAN Bing-hong, MIAO Mu-nan, ZHANG Kun
- 基于广义主成分分析法的我国高速公路服务设施平均间距研究
- Study on Average Spacing of Service Facilities in Chinese Expressway Based on Generalized PCA Algorithm
- 公路交通科技, 2017, 34(4): 108-114, 129
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(4): 108-114, 129
- 10.3969/j.issn.1002-0268.2017.04.016
-
文章历史
- 收稿日期: 2016-05-17
2. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710075
2. CCCC First Highway Consultants Co., Ltd., Xi'an Shaanxi 710075, China
公路的服务设施包括餐服务区、停车区和客运汽车停靠站[1]。本文研究对象为高速公路的服务设施,即服务区和停车区。一般而言,服务区规模较停车区大,且功能也相对较完善[2]。本文所提出的服务设施间距 (以下简称间距) 是指包括相邻服务区之间间距和停车区与服务区或相邻停车区之间间距。对于服务设施的研究,国内学者多数研究其设置规模,而对于间距的研究比较少且不够深入,如申旺从高速公路服务对象的需求、服务区的建设与经营成本、服务区的经济与社会效益等方面对服务区的布局进行分析研究,提出服务区分布的模型[3];刘亚非提出了低油量情况下车辆可行驶距离的计算模型,利用该模型对服务设施合理间距进行了计算。国内学者研究主要根据交通量和服务设施规模,结合已建服务设施的运营状况同时参考国外规定进行分析,大部分研究缺乏服务设施相关数据的调查和分析或者调查的服务设施数量太少,难以得出合理的结论,对我国服务设施的规划和建设也缺乏针对性的意见[4]。另外,目前服务设施的分布从总体上来说可以满足驾驶员疲劳特性和车辆加油的需求[5],但全国各地的服务设施数量和规模的需求并不一样,这就导致部分服务区吞吐能力不足、交通堵塞,而部分服务设施接近闲置,极大地浪费了资源。
《公路工程技术标准》[1](JTG B01—2014) 规定:高速公路应设置服务区,服务区平均间距宜为50 km,当沿线城镇分布稀疏,水、电等供给困难时,可增大服务区间距。高速公路应设置停车区,停车区可在服务区之间布设一处或多处,停车区与服务区或停车区之间的间距宜为15~25 km。《高速公路交通工程及沿线设施设计通用规范》[6](JTG D80—2006) 规定:服务区的平均间距不宜大于50 km,最大间距不宜大于60 km。停车区可在服务区之间布设一处或多处,其平均间距不宜大于15 km;最大间距不宜大于25 km。可见,规范对间距的要求也很笼统,不具有针对性。
因此,本文在对国内服务设施间距现状和间距影响因素进行详细调查的基础上,建立服务设施的间距计算模型,并提出针对我国现状的服务设施合理间距。
1 国内服务设施间距现状研究 1.1 服务设施间距数据收集本文的研究针对国内大部分高速公路服务设施间距。研究拟采用导航电子地图的方法来收集国内高速公路服务设施的间距,目前常用的导航地图较多,为了选择更加准确易用的导航地图,本文分别采用百度地图和搜狗地图,对G40福银高速陕西境内约80 km的路段的互通式立交间距进行测量。对比误差结果得,搜狗导航地图测量得到的间距与施工图数据的间距最大误差不超过0.1 km,精度较百度导航地图 (最大误差1.3 km) 高。因此利用搜狗导航地图来收集间距数据,收集了全国40条高速公路总计1 200个服务区和184个停车区的间距信息。涵盖了26个省及直辖市 (不含港澳台地区和西藏自治区) 的数据,涉及高速公路40条,总里程约7.5万km (调查间距数据时间截止到2013年底)。统计结果如图 1所示。
|
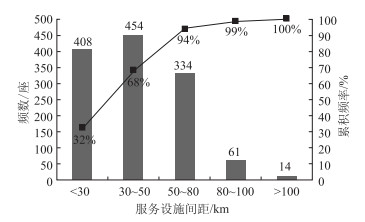
| 图 1 服务设施间距分布和累积曲线图 Fig. 1 Spacing distribution of service facilities and cumulative curve |
| |
从图 1可以看出,全国有68%的间距小于50 km,有94%的间距小于80 km,有99%的间距小于100 km。而平均间距计算图示如图 2所示,公式见式 (1)。利用该公式得出26个省市区的服务设施平均间距数据。
|
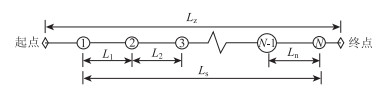
| 图 2 平均间距计算图示 Fig. 2 Schematic diagram of average spacing |
| |
图中L为间距平均值;Lz为高速公路总里程;Ls为高速公路服务设施分布长度;Li为相邻服务设施间距值;n为间距数量;N为高速公路服务设施数量。
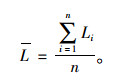
|
(1) |
服务设施的间距是多种因素共同作用的结果,从宏观角度来看,间距与区域经济、人口、汽车和客货运量等因素有着密切关系,通过分析调查的数据发现在经济发达、人口密集、汽车保有量大、客货运量大的地区,服务设施需求大,间距较小;反之,服务设施需求小,间距较大。
通过查阅《中国统计年鉴》[7](2014) 收集了经济、人口、公路里程、汽车和客货运量等相关数据 (数据统计截止到2013年底),并对处理后的各项数据与间距进行相关性分析 (本文相关性分析、主成分分析、回归分析等均使用IBM SPSS Statistics 22.0统计分析软件进行分析)。分析结果如下:
(1) 经济因素相关性分析
为了消除不同地区尤其是省和直辖市之间在国土面积的差异,本文采用GDP密度来进行分析,包括第一产业GDP密度 (亿元/万km2)、第二产业GDP密度 (亿元/万km2)、第三产业GDP密度 (亿元/万km2)。均采用式 (2) 计算。
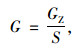
|
(2) |
式中,G为GDP密度;GZ为地区GDP值;S为地区的面积。相关性分析的结果如表 1所示。
| GDP密度 | 第一产业GDP密度 | 第二产业GDP密度 | 第三产业GDP密度 |
| Pearson相关性 | -0.680** | -0.555** | -0.601** |
| 显著性 (双侧) | 0 | 0.003 | 0.001 |
| 样本量 | 26 | 26 | 26 |
| 注:**为在0.01水平 (双侧) 上显著相关;*为在0.05水平 (双侧) 上显著相关,下同。 | |||
(2) 人口因素相关性分析
人口密度反映一个地区人口的稠密程度,人口密度主要包括城镇人口密度 (万人/万km2)、乡村人口密度 (万人/万km2)、常住人口密度 (万人/万km2)、流动人口密度 (万人/万km2)。人口密度均采用式 (3) 计算。相关性分析的结果如表 2所示。
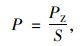
|
(3) |
| 人口密度 | 城镇人口密度 | 乡村人口密度 | 常住人口密度 | 流动人口密度 |
| Pearson相关性 | -0.610** | -0.650** | -0.635** | -0.592** |
| 显著性 (双侧) | 0.001 | 0 | 0 | 0.001 |
| 样本量 | 26 | 26 | 26 | 26 |
式中,P为人口密度;PZ为地区人口数量;S为地区的面积。
(3) 汽车数量因素相关分析
采用汽车密度进行车辆因素分析,汽车密度包括民用汽车密度 (万辆/万km2)、私人汽车密度 (万辆/万km2)、营用汽车密度 (万辆/万km2)。汽车密度均采用式 (4) 计算。相关性分析的结果如表 3所示。
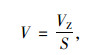
|
(4) |
| 汽车密度 | 民用汽车密度 | 私人汽车密度 | 营运汽车密度 |
| Pearson相关性 | -0.595** | -0.607** | -0.584** |
| 显著性 (双侧) | 0.001 | 0.001 | 0.002 |
| 样本量 | 26 | 26 | 26 |
式中,V为汽车密度;VZ为地区汽车拥有量;S为地区的面积。
(4) 客货运量因素相关分析
客货运量因素相关分析采用相应指标的密度进行分析,并用式 (5) 进行客货运量密度的计算。客货运量密度包括客运量密度 (万人/万km2)、货运量密度 (万吨/万km2)、旅客周转量密度[亿 (人·km)/万km2]、货物周转量密度[亿 (t·km)/万km2]、入境过夜游客密度 (万人/万km2)。客货运量密度相关性分析的结果如表 4所示。
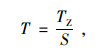
|
(5) |
| 客货运量密度 | 客运量密度 | 货运量密度 | 旅客周转量密度 | 货物周转量密度 | 入境过夜游客密度 |
| Pearson相关性 | -0.592** | -0.591** | -0.608** | -0.508** | -0.678** |
| 显著性 (双侧) | 0.001 | 0.001 | 0.001 | 0.008 | 0 |
| 样本量 | 26 | 26 | 26 | 26 | 26 |
式中,T为客货运量密度;TZ为地区客货运量;S为地区的面积。
1.3 服务设施间距影响因素的相关性分析由上述分析结果可知,Pearson相关系数绝对值均较大且为负值,各影响因素的P值均小于0.01,即表明一个地区服务设施平均间距与研究因素在统计学上有非常显著的相关性。并且第一产业GDP密度指标、常住人口密度指标、私人汽车密度指标以及入境过夜游客密度指标在其影响因素中的各项指
标与服务设施平均间距的相关程度最高。以此4个指标进行相关性分析得表 5,可知指标间的关系呈现出多、乱及部分相关的特点。
| Pearson相关性 | 第一产业GDP密度 | 常住人口密度 | 私人汽车密度 | 入境过夜游客密度 |
| 第一产业GDP密度 | 1 | 0.960** | 0.846** | 0.292 |
| 常住人口密度 | 0.960** | 1 | 0.839** | 0.337 |
| 私人汽车密度 | 0.846** | 0.839** | 1 | 0.471* |
| 境过夜游客密度 | 0.292 | 0.337 | 0.471* | 1 |
2 服务设施平均间距计算模型
经上分析知,有必要提炼出各原始指标中有用的信息,减少指标间的相关程度,尽可能保留各指标所含有用信息。采用主成分分析的方法可以进行指标数的降维,通过各因素之间的内在关系,合理选取主要因素。此外,根据《高速公路交通工程及沿线设施设计通用规范》[6](JTG D80—2006) 最大间距60 km的规定进行样本筛选,去掉不满足规范的青海省 (平均间距为73.1 km) 样本,即其他样本均为满足要求的有效样本。
2.1 广义主成分分析法主成分分析是一种常用的多元统计分析方法[8-10],基本思想是通过常线性变换的方法把原始相关的变量转换为不相关的数量较少的新变量,对有较强线性特征的指标具有较好的压缩作用[11-17]。主成分分析法,一般包括线性主成分分析法、二次主成分分析法以及“对数-线性”广义主成分分析法[18]。但经试算表明,与“对数-线性”广义主成分分析法相比,运用线性主成分分析法 (即使用原始的指标数据) 指标共同度较低,指标中的信息提取度不高,并且构造的新综合指标难以同间距数据进行回归分析;二次广义主成分分析法主成分数量过多,降维效果较差,对后期回归分析造成较大困难,对比结果如表 6所示。
2.2 数据转换
(1) 合成数据转换
对影响间距的指标进行编号依次为 (X1, X2, …,X14, X15),将统计的各省市区的各项指标组合成矩阵为Xij(1≤i≤25,1≤j≤15),其中xij均为正值。对Xij进行如式 (6) 转换得到合成数据矩阵Aij。
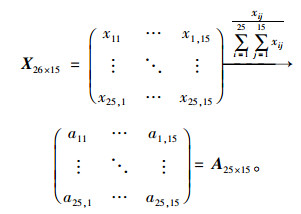
|
(6) |
(2) 建立“对数-中心化”协方差阵:
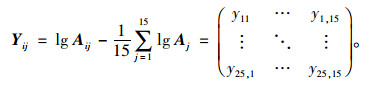
|
(7) |
(3) 对Xij标准化,计算样本相关阵:
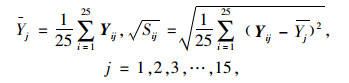
|
令
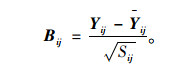
|
(8) |
得标准化数矩阵B=(Bij),计算相关矩阵R:
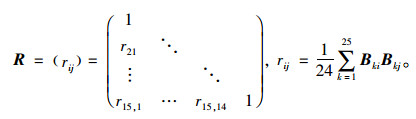
|
(9) |
(4) 求R的特征值和特征向量:
不妨设λ1≥λ2≥…≥λ15>0,结果如表 7所示。则λj所对应的特征向量为: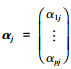
| 初始特征值 | λ1 | λ2 | λ3 | λ4 | λ5 | λ6 | … | λ15 |
| 特征值 | 13.561 | 0.529 | 0.326 | 0.225 | 0.162 | 0.076 | … | 0.000 |
| 方差百分比/% | 90.409 | 3.526 | 2.176 | 1.499 | 1.083 | 0.510 | … | 0.002 |
| 累计方差/% | 90.409 | 93.934 | 96.110 | 97.609 | 98.692 | 99.202 | … | 100.000 |
2.3 建立主成分
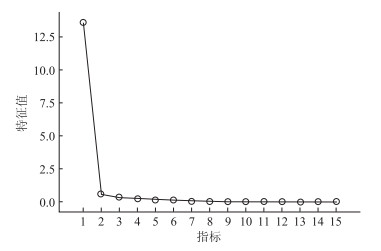
由碎石图 (见图 3) 可知,特征值从λ2开始趋于平缓,仅有λ1的值大于1,且累计方差贡献率λ1为90.409%,满足累计方差贡献率大于85%的一般选取标准,因此选择第一个因子作分析:
|
| 图 3 特征值碎石图 Fig. 3 Scree plot of characteristic values |
| |
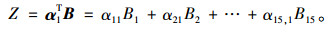
|
(10) |
由此可以计算出主成分评分矩阵Z=(0.597 61, 0.137 23, -2.024 57, 0.609 71, -0.354 82, -1.009 41, 1.387 27, 1.131 91, 0.795 41, 0.447 36, 0.120 48, 1.138 75, 0.865 28, 0.343 91, 0.329 71, 1.196 60, -0.123 84, 0.519 20, -0.373 02, -0.269 17, -0.660 14, -0.058 71, -1.576 22, -0.635 27, -2.535 26)T。
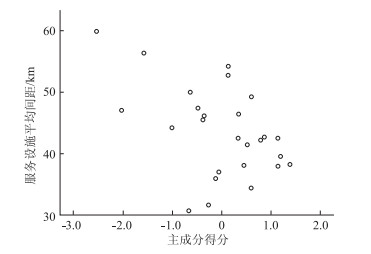
2.4 非线性回归模型建立首先绘制服务设施平均间距与主成分得分的散点图,见图 4,从中分析两者之间存在的关系。
|
| 图 4 服务设施平均间距与主成分评分散点图 Fig. 4 Scatter diagram of average spacing of service facilities and principal component score |
| |
由于散点图中近似同一得分的间距值分布较散,并且在得分0.5附近分布较集中,从散点图中我们很难直观地找出自变量与因变量之间的最优关系,因此,本文对得分及对应的间距进行分组取均值 (得分遵循组距分组原则分为7组),再利用几种常用的函数对处理后的数据进行分析,利用SPSS软件进行直线和曲线估计得表 8。
| 方程式 | R2 | F | df1 | df2 | Sig (显著性) |
| 线性 | 0.760 | 15.842 | 1 | 5 | 0.011 |
| 逆模型 | 0.048 | 0.251 | 1 | 5 | 0.638 |
| 二次 | 0.801 | 7.980 | 2 | 4 | 0.040 |
| 立方 | 0.831 | 4.927 | 3 | 3 | 0.112 |
| 复合 | 0.787 | 18.468 | 1 | 5 | 0.008 |
| S函数 | 0.046 | 0.242 | 1 | 5 | 0.644 |
| 增长 | 0.787 | 18.468 | 1 | 5 | 0.008 |
| 指数 | 0.787 | 18.468 | 1 | 5 | 0.008 |
从表 8可以分析出,线性、二次、复合、增长、指数5个模型的Sig小于0.05,表明差异性显著,其中立方函数模型的R2值最大,最接近1。因此,选择二次模型计算。利用SPSS软件能够计算出各项系数如表 9所示,并绘制函数曲线,见图 5。

|
| 图 5 函数曲线图 Fig. 5 Function curves |
| |
| 自变量 | 系数值 | F | df1 | t | 显著性 |
| Z | -3.443 | 1.730 | -0.657 | -1.981 | 0.117 |
| Z2 | 0.998 | 1.124 | 0.293 | 0.888 | 0.425 |
| (常量) | 42.679 | 1.760 | — | 24.248 | 0.000 |
回归出的服务设施平均间距计算公式为:
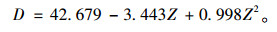
|
(11) |
(1) 对模型进行相关性检验,结果如表 10所示。
| 模型 | R | R2 | 调整R2 | 标准估计的误差 |
| 二次函数 | 0.895 | 0.801 | 0.699 | 3.428 |
由上表知,R2=0.801>0.8,则可以判断二次函数模型的拟合程度较为理想[11]。
(2) 方差分析
分析得表 11,F统计量为7.980,显著性值为0.040小于0.05的显著性水平,说明这两者之间存在较高显著度的立方函数关系。综上可得,该二次函数模型具有统计学上的意义。
| 平方和 | 自由度 | 均方 | F | 显著性 | |
| 回归/R | 187.634 | 2 | 93.817 | 7.980 | 0.040 |
| 残差 | 47.024 | 4 | 11.756 | — | — |
| 总计 | 234.658 | 6 | — | — | — |
(3) 应用回归方程带入各个省市区的相关数据,计算各省服务设施平均间距的模型计算值。结果如表 12所示。
| 省市区 | 服务设施间距/km | |||
| 实测值 | 模型计算值 | |||
| 东部地区 | 河北 | 34.4 | < | 41.0 |
| 辽宁 | 49.3 | > | 41.0 | |
| 江苏 | 38.3 | < | 39.8 | |
| 浙江 | 42.5 | > | 40.1 | |
| 福建 | 38.1 | < | 41.3 | |
| 广东 | 39.5 | < | 40.0 | |
| 山东 | 37.9 | < | 40.1 | |
| 中部地区 | 山西 | 54.2 | > | 42.2 |
| 内蒙古 | 47.1 | < | 53.7 | |
| 吉林 | 46.1 | > | 44.0 | |
| 黑龙江 | 44.8 | < | 47.2 | |
| 安徽 | 42.2 | > | 40.6 | |
| 江西 | 52.8 | > | 42.3 | |
| 河南 | 42.7 | > | 40.4 | |
| 湖北 | 46.4 | > | 41.6 | |
| 湖南 | 42.5 | > | 41.7 | |
| 广西 | 36.0 | < | 43.1 | |
| 西部地区 | 重庆 | 41.4 | > | 41.2 |
| 四川 | 45.5 | > | 44.1 | |
| 贵州 | 31.6 | < | 43.7 | |
| 云南 | 30.7 | < | 45.4 | |
| 陕西 | 37.0 | < | 42.9 | |
| 甘肃 | 56.3 | > | 50.6 | |
| 宁夏 | 50.0 | > | 45.3 | |
| 新疆 | 59.8 | > | 57.8 | |
根据模型的计算结果可知,服务设施合理平均间距一般在40~50 km,东部地区合理平均间距为40 km,中部地区为44 km,西部地区为46 km,各地区的合理平均间距符合规范要求及实际情况。
3 结论(1) 在对我国各省 (包含重庆直辖市) 服务设施实际间距以及相关因素进行广泛调查的基础上,采用“对数-线性”广义主成分分析法分析提炼各因素之间的内在关系,计算得出各省因素的综合得分,之后采用曲线估计的方法拟合出服务设施平均间距的计算模型并得出我国各省服务设施合理平均间距。该方法将与服务设施平均间距有关的15个影响因素降维至1个主成分指标,有效地挖掘出各因素与平均间距之间的关系,因此该方法合理有效。
(2) 研究表明:第一产业GDP密度指标、常住人口密度指标、私人汽车密度指标以及入境过夜游客密度指标是各因素中影响服务设施平均间距的主要指标;分析模型计算结果可得,我国东部地区服务设施的合理平均间距为40 km,中部地区为44 km,西部地区为46 km。
(3) 该模型的提出可以在实际工作中得到应用。在服务设施规划阶段,若没有交通量资料,设计人员只能根据以往的建设经验对间距进行选择,带有很大的主观性。利用该模型方程,根据当地的GDP和人口数量等相关多项预测数据,结合以往的建设经验,可以更可靠地计算出当地的合理间距预测值作为参考。此外,一个地区现有的服务设施间距是否还能满足当地的需求也可以通过该地区实际各项指标值运用本模型进行评价。
(4) 除本文统计的服务设施间距影响因素外可能还有其他相关性较高的因素 (如:规模、配置、行车便利性等),有待今后进一步的研究分析。
| [1] | JTG B01—2014, 公路工程技术标准[S]. JTG B01—2014, Technical Standard of Highway Engineering[S]. |
| [2] | 汤毅. 高速公路服务区规划的关键技术研究[D]. 西安: 长安大学, 2008. TANG Yi. Study on Key Technologies of Expressway Service Area Planning[D]. Xi'an:Chang'an University, 2008. |
| [3] | 申旺. 高速公路服务区规划与管理研究[D]. 西安: 长安大学, 2010. SHEN Wang. Study on Planning and Management of Highway Service Area[D]. Xi'an:Chang'an University, 2010. |
| [4] | 刘亚非. 高速公路服务设施关键技术标准研究[D]. 西安: 长安大学, 2012. LIU Ya-fei. Study on Key Technical Standard of Expressway Service Facility[D]. Xi'an:Chang'an University, 2012. |
| [5] | 曾志刚. 高速公路硬路肩的功能与宽度值研究[D]. 西安: 长安大学, 2012. Z ENG Zhi-gang. Study on Function and Width of Expressway Hard Shoulder[D]. Xi'an:Chang'an University, 2012. |
| [6] | JTG D80—2006, 高速公路交通工程及沿线设施设计通用规范[S]. JTG D80—2006, General Specification of Freeway Traffic Engineering and Roadside Facilities[S]. |
| [7] | 国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 2013. National Bureau of Statistics. China Statistical Yearbook[M]. Beijing: China Statistics Press, 2013. |
| [8] | 孙占全, 潘景山, 张赞军, 等. 基于主成分分析与支持向量机结合的交通流预测[J]. 公路交通科技, 2009, 26(5): 127-131 SUN Zhan-quan, PAN Jing-shan, ZHANG Zan-jun, et al. Traffic Flow Forecast Based on Combining Principal Component Analysis with Support Vector Machine[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 127-131 |
| [9] | 吴明, 王莹莹, 冯琪. 基于主成分分析的综合运输通道布局模型研究[J]. 公路交通科技, 2011, 28(1): 154-158 WU Ming, WANG Ying-ying, FENG Qi. Research on Comprehensive Transportation Channel Layout Model Based on Main Component Analysis[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 154-158 |
| [10] | 蒋惠园, 王晚香. 主成分分析法在综合评价中的应用[J]. 武汉理工大学学报:交通科学与工程版, 2004, 28(3): 467-471 JIANG Hui-yuan, WANG Wan-xiang. Application of Principal Component Analysis in Synthetic Appraisal for Multi-objects Decision-making[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering Editon, 2004, 28(3): 467-471 |
| [11] | 顾政华, 李旭宏. 主成分分析法在公路网综合评价中的应用[J]. 公路交通科技, 2003, 20(5): 71-74 GU Zheng-hua, LI Xu-hong. Application of Principal Component Analysis Method in Comprehensive Evaluation for Road Network[J]. Journal of Highway and Transportation Research and Development, 2003, 20(5): 71-74 |
| [12] | 董胜伟, 苏婷, 贾利新. 基于主成分分析的安阳市公交系统模糊综合评价[J]. 河南科学, 2016, 34(5): 775-780 DONG Sheng-wei, SU Ting, JIA Li-xin. Fuzzy Comprehensive Evaluation on Transport System of Anyang City Based on Principal Component Analysis[J]. Henan Science, 2016, 34(5): 775-780 |
| [13] | 孙刘平, 钱吴勇. 基于主成分分析法的综合评价方法的改进[J]. 数学的时间与认识, 2009, 39(18): 15-20 SUN Liu-ping, QIAN Wu-yong. An Improved Method Based on Principal Component Analysis for the Comprehensive Evaluation[J]. Mathematics in Practice and Theory, 2009, 39(18): 15-20 |
| [14] | 柴纯纯, 徐得潜, 张浏, 等. 基于模糊层次-主成分分析法的城市河道生态护坡综合评价[J]. 水土保持通报, 2016, 36(5): 167-177 CHAI Chun-chun, XU De-qian, ZHANG Liu, et al. Comprehensive Assessment on Ecological Revetment of Urban River Course Using Fuzzy Analytic Hierarchy Process and Principal Component Analysis[J]. Bulletin of Soil and Water Conservation, 2016, 36(5): 167-177 |
| [15] | 张喜成. 区域综合交通发展规划的若干关键问题研究[D]. 成都: 西南交通大学, 2011. ZHANG Xi-cheng. Research on Key Problems of Regional Transportation Planning[D]. Chengdu: Southwest Jiaotong University, 2011. |
| [16] | 吴亚非, 李科. 基于SPSS的主成分分析法在评价体系中的应用[J]. 当代经济, 2009(3): 166-168 WU Ya-fei, LI Ke. Application of Principal Component Analysis Based on SPSS in Evaluation System[J]. Contemporary Economics, 2009(3): 166-168 |
| [17] | 顾绍红, 王永生, 王光霞. 主成分分析模型在数据处理中的应用[J]. 测绘科学技术学报, 2007, 24(5): 387-390 GU Shao-hong, WANG Yong-sheng, WANG Guang-xia. Application of Principal Component Analysis Model in Data Processing[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2007, 24(5): 387-390 |
| [18] | 陈光亭, 裘哲勇. 数学建模[M]. 北京: 高等教育出版社, 2014. CHEN Guang-ting, QIU Zhe-yong. Mathematical Modeling[M]. Beijing: Higher Education Press, 2014. |
| [19] | 郝黎仁, 樊元, 郝哲欧. SPSS实用统计分析[M]. 北京: 中国水利水电出版社, 2003. HAO Li-ren, FAN Yuan, HAO Zhe-ou. SPSS Practical Statistic Analysis[M]. Beijing: China Water & Power Press, 2003. |
 2017, Vol. 34
2017, Vol. 34
