扩展功能
文章信息
- 李文杰, 侯天宇, 赵君黎, 冯苠
- LI Wen-jie, HOU Tian-yu, ZHAO Jun-li, FENG Min
- 基于可靠度理论的混凝土桥梁安全性评估方法研究
- Study on Safety Evaluation Method for Concrete Bridges Based on Reliability Theory
- 公路交通科技, 2017, 34(4): 87-92
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(4): 87-92
- 10.3969/j.issn.1002-0268.2017.04.013
-
文章历史
- 收稿日期: 2016-05-11
2. 中交公路规划设计院有限公司, 北京 100088
2. CCCC Highway Consultants Co., Ltd., Beijing 100088, China
作为一种人工构筑物,在环境、荷载、材料性能退化等多重因素影响下,公路混凝土桥梁在其全寿命周期内结构材料性能是不断退化的,材料性能的衰变主要表现为混凝土强度降低、保护层碳化、钢筋锈蚀等微观性能的退化,进而导致构件层面出现变形增大、裂缝扩展、构件破坏等宏观性能退化特征。除此之外,作为影响中小跨径桥梁结构安全性和耐久性的重要因素,汽车荷载的作用加快了结构抗力的退化进程,特别是在当前公路交通运输需求不断增长的背景下,实际运营车辆的数量和重量均出现了大幅提高,导致桥梁实际荷载水平与设计预期荷载水平之间存在很大差异。公路交通运输需求的增长与结构性能衰变之间的矛盾日益突出,加速了公路桥梁的性能劣化。随着大量桥梁短期内投入运营,未来一段时期将有大量的在役混凝土桥梁发生不同程度的劣化和损伤,需要对这些桥梁进行科学评估后才能明确进一步的处置措施。显然,不合理的评估结果将会造成巨大的资源浪费或带来较大的安全隐患。因此,如何客观评价在役混凝土桥梁安全性至关重要。
众所周知,随着桥梁工程设计理论与方法的发展,以可靠度理论为基础的概率极限状态设计方法已经成为公路桥梁结构的主流设计方法[1-2]。以此为基础,公路桥梁的承载能力评定也正逐步由传统基于外观检查和专家经验的定性评估方法逐步过渡到以无损检测和荷载试验相结合且基于概率理论的检测评定方法[3]。目前公路桥梁的承载能力评定主要通过现场实测,定性与定量相结合来分析桥梁构件的损伤程度,进而确定旧桥承载能力恶化系数,并未将抗力和荷载统筹考虑。而桥梁的安全性是抗力和荷载效应的综合反映,因此,利用可靠度理论综合考虑结构抗力的衰减和汽车荷载效应的增长对桥梁安全性的影响将是公路桥梁安全性评估的主流方法。
为获得符合工程实际的在役混凝土桥梁安全性评估方法,本文引入汽车荷载效应调整系数和抗力调整系数,确定了在役桥梁安全性评估表达式和目标可靠指标,建立了在役混凝土桥梁可靠度评估方法,进而通过分析在役混凝土桥梁临界汽车荷载效应调整系数与临界抗力调整系数之间的关系,建立了基于“双控”思想的在役混凝土桥梁安全性实用评估方法。
1 基于调整系数的在役混凝土桥梁安全性评估 1.1 评估表达式设计使用年限内,随混凝土桥梁的抗力逐渐下降及荷载效应的增加,桥梁实际可靠指标不断下降。当实际可靠指标低于在役桥梁安全性评定目标可靠指标时,桥梁不满足安全性能需求,需采取车辆限重或结构加固等措施。据此,本文引入汽车荷载调整系数ξQ和抗力调整系数ξR对《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)[4]中规定的承载能力设计表达式进行调整,以此反映公路桥梁汽车荷载效应与抗力的变化,在役桥梁安全性评估表达式可表示为:
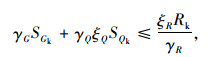
|
(1) |
式中,ξQ=SQr/SQk,SQr为实际运营汽车荷载效应; SQk为设计规范规定的汽车荷载效应标准值;ξR=Rr/Rk,Rr为实际抗力,Rk为根据设计规范计算的结构或构件满足安全性能要求的最低抗力标准值 (后文简称为计算抗力标准值)。应当明确的是,由于许多桥梁在设计时预留了很大的安全储备,因此,一般情况下Rk与实桥抗力标准值不相等,即初始状态下的抗力调整系数大于1;SGk为设计阶段实桥恒载效应标准值;γG,γQ和γR分别为恒载分项系数、汽车荷载分项系数和抗力分项系数。本文选取轴心受压构件作为脆性破坏构件 (包括轴压构件和受剪构件) 的代表,轴心受拉构件作为延性破坏构件 (包括轴心受拉构件、受弯构件和大偏心受压构件) 的代表,其设计表达式的分项系数如表 1所示。
| 构件分类 | γG | γQ | γR |
| 脆性破坏控制 | 1.2 | 1.4 | 1.45 |
| 延性破坏控制 | 1.2 | 1.4 | 1.2 |
根据式 (1),当ξR < 1时,实际抗力小于桥梁设计时满足安全性能要求的最低抗力标准值,桥梁结构或构件受损,按照承载能力评估表达式计算出的可靠指标降低。当ξQ>1时,实际汽车荷载效应大于桥梁设计时汽车荷载效应标准值,表明实际运营汽车荷载效应大于设计汽车荷载标准效应,按照承载能力评估表达式计算得出的可靠指标降低。
1.2 考虑调整系数后公路桥梁汽车荷载与抗力的统计特征在可靠度分析过程中,需要确定荷载效应和抗力的平均值和标准差。但由安全性评估表达式的定义可知,汽车荷载调整系数ξQ和抗力调整系数ξR反映的是实际值与标准值之间的关系。因此,为进行可靠性评估,应分别对汽车荷载分布模型和抗力分布模型进行分析,确定汽车荷载效应标准值,和计算抗力标准值与均值和标准差之间的关系,进而确定汽车荷载调整系数ξQ和抗力调整系数ξR对其平均值和标准差的影响。
(1) 汽车荷载效应统计特征
工程经验表明,公路桥梁汽车荷载效应设计基准期的最大值服从极值Ⅰ型分布[5]:
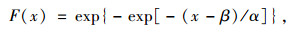
|
(2) |
式中α和β为实际汽车荷载的分布参数,根据极值Ⅰ型分布的统计特征可知:
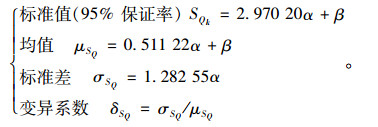
|
(3) |
由式 (3) 可得:
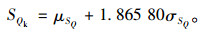
|
(4) |
由此可知SQk与μSQ和σSQ为线性关系,假定反映汽车荷载效应离散程度的变异系数δSQ不变,可得当SQk变为ξQSQk时,μSQ和σSQ分别为ξQμSQ和ξQσSQ。
(2) 抗力统计特征
工程经验表明,公路桥梁的结构抗力服从对数正态分布:
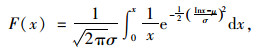
|
(5) |
式中,
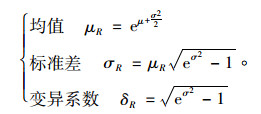
|
(6) |
假定不同规范计算确定的结构或构件满足安全性能要求的最低抗力标准值的保证率为φ,将 (1-φ) 代入标准正态分布表可确定参数ω(ω < 0),使得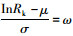
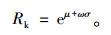
|
(7) |
假定反映抗力离散程度的变异系数δR保持不变,即σ保持不变,由式 (6) 和式 (7) 可得:
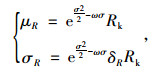
|
(8) |
所以,μR和σR均与Rk成正比,当Rk变为ξRRk时,μR和σR分别为ξRμR和ξRσR。
1.3 在役混凝土桥梁安全性评估目标可靠指标《公路工程结构可靠度设计统一标准》(GB/T 50283—1999)[6]中给定了公路桥梁设计阶段混凝土结构目标可靠指标,如表 2所示。然而,已有研究指出[7],设计规范需保证结构在整个服役期间的安全使用,而对在役桥梁评估,仅需要保证桥梁在评估间隔时段的安全性;从经济性角度,在使用阶段和设计阶段提高相同程度的桥梁承载能力时,使用阶段所需的经费远大于设计阶段,且需要解决许多的技术难题[8],因此有必要在设计目标可靠指标的基础上,通过适当的折减获得适用于安全性评估的目标可靠指标。需要指明的是,当降低目标可靠指标时,结构的失效风险也将增大。英国、荷兰、澳大利亚等国家对于在役结构的可接受风险比新建结构高一个数量级,由此推定在役结构的年最大允许失效概率也应比新建结构高一个数量级[9];美国规范中评估目标可靠指标为2.5,设计目标可靠指标为3.5[10],折算成最大允许失效概率后分别为6.2×10-3和2.3×10-4,略大于一个数量级;加拿大规范中规定对于构件失效仅会导致局部失效、失效前具有明显预兆并且评估者可以获得充分且有效的检查记录数据做出评估的结构构件,评估目标可靠指标为2.75,设计阶段目标可靠指标为3.5,折算成年最大允许失效概率分别为3×10-3和2.3×10-4,约相差一个数量级。因此本文首先将我国公路桥梁设计阶段混凝土结构的目标可靠指标换算为最大允许失效概率,通过对设计阶段的最大允许失效概率提高一个数量级,得到在役结构最大允许失效概率,据此推算出在役桥梁安全性评估目标可靠指标如表 3所示。
| 规范 | 由延性破坏控制的构件 | 由脆性破坏控制的构件 | |
| 04规范 | 三级 | 3.7 | 4.2 |
| 二级 | 4.2 | 4.7 | |
| 一级 | 4.7 | 5.2 | |
| 规范 | 由延性破坏控制的构件 | 由脆性破坏控制的构件 | |
| 04规范 | 三级 | 3.1 | 3.7 |
| 二级 | 3.7 | 4.2 | |
| 一级 | 4.2 | 4.8 | |
1.4 在役混凝土桥梁可靠度评估
根据上述在役混凝土桥梁安全性评估目标可靠指标和式 (1),即可利用可靠度理论确定汽车荷载调整系数ξQ和结构抗力调整系数ξR取不同值时,桥梁是否满足安全性能要求,具体步骤如下:
(1) 利用已有桥梁检测数据确定汽车荷载调整系数ξQ和结构抗力调整系数ξR的取值。
(2) 计算考虑调整系数后汽车荷载和抗力的统计参数。其中,在制订现行《公路工程结构可靠度设计统一标准》(GB/T 50283—1999)[11]时,通过大量的数据收集和统计分析,得出了恒载、活载和抗力的统计参数,可作为桥梁初始状态的统计参数。
(3) 利用式 (1) 并采用JC法计算出一般运行和密集运行两种状态下,不同活荷载效应与恒荷载效应标准值的比值ρ下的可靠指标,ρ分别取0.1,0.25,0.5,1.0,1.5和2.5,取其平均值作为该荷载和抗力调整系数情况下的可靠度代表值[12]。
(4) 计算结果与目标可靠指标进行对比:如果计算确定的可靠度大于到评估目标可靠指标,则满足安全性能要求;如果与计算确定的可靠度小于评估目标可靠指标,则不满足安全性能要求。
2 基于“双控”思想的混凝土桥梁安全性实用评估方法 2.1 汽车荷载和抗力调整系数临界值由上述分析可知,由于在役混凝土桥梁目标可靠指标为定值,为保证结构的安全性能,ξR和ξQ的临界值之间存在一一对应的关系,通过确定两个临界值之间的关系,即可直接对桥梁安全性能进行评估,这样就避免了复杂的可靠指标计算,便于工程应用。
由于安全储备、旧桥加固和汽车荷载限重等因素的影响,存在旧桥抗力大于计算抗力标准值或汽车荷载效应小于原设计标准值的可能。因此,取抗力调整系数ξR=0.70,0.75,0.80,0.85,0.90,0.95,1.00,1.05,1.10,1.15,1.20;汽车荷载调整系数ξQ以0.3为起始最小值,按照0.1的级差递增取值,利用1.2节所述方法确定考虑调整系数后的汽车荷载效应和抗力统计特征,并以此为依据计算目标可靠指标,直至计算出的可靠指标不满足在役桥梁的目标可靠指标。这样既可确定抗力一定时,在役桥梁在满足安全性评估目标可靠指标的情况下,所能承受的最大汽车荷载效应,可为该桥荷载管控提供决策依据,同时,也可以确定在当前汽车荷载水准下,在役桥梁满足目标可靠指标的情况下所需的抗力,进而可根据实际承载能力评定结果,选择合适的处理措施 (加固或不采取措施)。
根据上述分析,可以确定抗力调整系数为ξR时,不满足承载能力评估目标可靠指标要求的汽车荷载调整系数临界值ξ′Q。同时,也可确定出汽车荷载调整系数为ξQ时,不满足承载能力评估目标可靠指标要求的抗力调整系数临界值ξ′R。计算结果见表 4。
| ξ′Q | ξ′R | |||||||||||
| 1.20 | 1.15 | 1.10 | 1.05 | 1.00 | 0.95 | 0.90 | 0.85 | 0.80 | 0.75 | 0.70 | ||
| 一级 | 延性破坏 | 1.8 | 1.6 | 1.5 | 1.3 | 1.2 | 1.0 | 0.9 | 0.7 | 0.6 | 0.5 | 0.3 |
| 脆性破坏 | 2.8 | 2.6 | 2.4 | 2.2 | 2.0 | 1.8 | 1.6 | 1.4 | 1.3 | 1.1 | 0.9 | |
| 二级 | 延性破坏 | 1.7 | 1.6 | 1.4 | 1.3 | 1.1 | 1.0 | 0.9 | 0.7 | 0.5 | 0.4 | 0.3 |
| 脆性破坏 | 2.9 | 2.7 | 2.5 | 2.3 | 2.1 | 1.8 | 1.6 | 1.4 | 1.2 | 1.1 | 0.9 | |
| 三级 | 延性破坏 | 1.7 | 1.5 | 1.4 | 1.2 | 1.1 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 | 0.3 |
| 脆性破坏 | 2.8 | 2.6 | 2.4 | 2.2 | 2.0 | 1.8 | 1.6 | 1.4 | 1.2 | 1.0 | 0.8 | |
2.2 基于“双控”思想的混凝土桥梁安全性实用评估方法
根据上述思想,可确定两种在役混凝土桥梁承载能力评估方法,一是根据实际运营汽车效应确定满足安全性要求时的抗力,即抗力控制法;二是根据抗力确定满足安全性能要求时的最大汽车荷载效应,即汽车荷载效应控制法。本文将这两种方法统称为“双控”(抗力和汽车荷载效应) 评估方法。具体实施过程如下所述:
(1) 抗力控制法
① 根据《公路桥梁承载能力检测评定规程》(JTG/T J21—2011)[13]中的规定选取需要检测与评定构件,利用实测汽车荷载数据计算汽车荷载效应SQr,进而确定汽车荷载调整系数ξQ(ξQ=SQrk/SQk)。
② 令ξ′Q=ξQ,根据表 4查找对应的临界抗力调整系数ξ′R。
③ 计算满足安全性能的最小抗力值R′r(R′r=ξ′RRk)。当实桥抗力Rr < R′r时,需进行加固处理。
(2) 汽车荷载效应控制法
① 根据《公路桥梁承载能力检测评定规程》(JTG/T J21—2011) 中的规定选取需要的检测与评定构件,利用实桥承载能力评定结果确定桥梁抗力值Rr,进而计算抗力调整系数ξR(ξR=Rr/Rk)。
② 令ξ′R=ξR,根据表 4查找对应的临界汽车荷载效应调整系数ξ′Q。
③ 计算满足安全性能的最大汽车荷载值S′Qr(S′Qr=ξ′QSQk)。当实桥汽车荷载效应SQr>S′Qr时,需限定过桥车辆荷载。
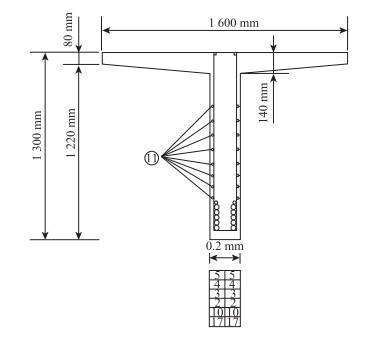
3 评估实例某二级RC简支T梁桥计算跨径20 m,桥宽为10.6 m,C30混凝土,HRB335级钢筋,主梁跨中截面配筋布置分别如图 1所示, 单片梁钢筋数量如表 5所示。该桥梁设计汽车荷载等级为公路-Ⅰ级。对当前实桥状况进行检测,该桥承载能力检算系数Z1=1.03,承载能力恶化系数ξe=0.11,钢筋的截面折减系数ξs=0.90。由于本桥进行了承载能力评定,因此,安全性评估采用汽车荷载效应控制法。
|
| 图 1 跨中截面配筋布置图 Fig. 1 Reinforcement arrangement of mid-span section |
| |
| 编号 | 直径/mm | 长度/mm | 根数 |
| 2 | ϕ32 | 2 103.6 | 2 |
| 3 | ϕ32 | 1 963.4 | 2 |
| 4 | ϕ32 | 1 673.6 | 2 |
| 5 | ϕ25 | 1 343.8 | 2 |
| 10 | ϕ32 | 1 990.0 | 2 |
| 17 | ϕ32 | 1 990.0 | 2 |
| 11 | ϕ8 | 2 000.0 | 16 |
对于抗力调整系数,首先根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004) 计算出该桥的计算抗力标准值Rk为2 275.50 kN·m,而设计阶段实桥抗力标准值为3 495.60 kN·m,可见该桥在设计阶段具有很大的安全储备。利用《公路桥梁承载能力检测评定规程》(JTG/T J21—2011) 中规定的在役桥梁承载能力计算方法计算当前实际抗力Rr为3 162.03 kN·m,所以该桥抗力调整系数ξR为1.389 6。令ξ′R=ξR=1.389 6,根据表 4,线性插值可得临界汽车荷载效应调整系数为ξ′Q≈2.2,即该桥当前所能承受的最大实际汽车荷载效应为04规范汽车荷载效应标准值的2.2倍。
对于汽车荷载效应调整系数,首先根据《公路桥涵设计通用规范》(JTG D60—2004) 中的规定计算出该桥汽车荷载效应标准值为670.67 kN·m。由于汽车荷载效应受地域和使用时期的影响较大,其统计参数在使用阶段发生了较大的变化。因此,本文利用该桥所在区域典型路段的WIM实测数据对汽车荷载进行统计分析,结果表明:一般运行状态下,实际汽车荷载效应服从极值Ⅰ型分布,其平均值μSQ=543.50 kN·m,标准差σSQ=74.48 kN·m;密集运行状态下,实际汽车荷载效应同样服从极值Ⅰ型分布,其平均值μ′SQ=929.65 kN·m,标准差σ′SQ=176.49 kN·m。由式 (4) 可得一般运行状态和密集运行状态下实际汽车荷载效应代表值分别为682.46 kN·m和1 258.95 kN·m,据此求得一般运行状态和密集运行状态下汽车荷载效应调整系数分别为1.1和1.9,均小于临界汽车荷载效应调整系数,即该桥满足安全性要求。该计算结果当前检测报告结果一致,可见采用基于“双控”思想的混凝土桥梁安全性实用评估方法进行安全性评定是可行的。
4 结论本文通过研究提出了汽车荷载效应调整系数和抗力调整系数的概念,确定了在役混凝土桥梁安全性能评估表达式,并建立了在役混凝土桥梁的可靠度评估方法。在此基础上,提出了在役混凝土桥梁安全性实用评估方法——基于“双控”思想的混凝土桥梁安全性评估方法,得出了以下结论:
(1) 引入调整系数的在役混凝土桥梁安全性评估表达式可同时考虑抗力与汽车荷载效应的影响,更符合实际情况,据此可得出更合理的评估结果。
(2) 根据国外相关规范,在役桥梁最大允许失效概率较新建桥梁高一个数量级,由此可以确定在役桥梁安全性评估的目标可靠指标。
(3) 除直接利用评估表达式对在役桥梁进行可靠度评估外,可利用本文提出的基于“双控”思想的混凝土桥梁安全性实用评估方法进行安全性评估,这样可以避免复杂的可靠度运算,便于工程应用。实桥评估算例表明,该实用方法简便可行。
| [1] | ANG H S, TANG W H. Probability Concepts in Engineering Planning and Design (Vol. 1)[M]. New York: John Wiley, 2007. |
| [2] | 贡金鑫, 魏巍巍. 工程结构可靠度设计原理[M]. 北京: 机械工业出版社, 2007. GONG Jin-xin, WEI Wei-wei. Reliability Design Principles of Engineering Structure[M]. Beijing: China Machine Press, 2007. |
| [3] | 李文杰, 张旭, 贡金鑫, 等. 工程结构设计理论与方法的发展与趋势[C]//2014工程结构可靠性设计理论、方法与应用学术研讨会论文集. 大连: 计算力学学报编辑部, 2014: 27-33. LI Wen-jie, ZHANG Xu, GONG Jin-xin, et al. Developments and Trends for Theories and Methods of Engineering Structure Design[C]//Conference Proceedings of Symposium on the Theory, Method and Application of Reliability Design for Engineering Structures. Dalian: Editorial Department of Chinese Journal of Computational Mechanics, 2014:27-33. |
| [4] | JTG D62—2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62—2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S]. |
| [5] | 李杨海, 鲍卫刚, 郭修武, 等. 公路桥梁结构可靠度与概率极限状态设计[M]. 北京: 人民交通出版社, 1997. LI Yang-hai, BAO Wei-gang, GUO Xiu-wu, et al. Reliability and Probability Limit State Design of Highway Bridges[M]. Beijing: China Communications Press, 1997. |
| [6] | GB/T 50283—1999, 公路工程结构可靠度设计统一标准[S]. GB/T 50283—1999, Unified Standard for Reliability Design of Highway Engineering Structures [S]. |
| [7] | 尤吉, 房涛, 付公康. 公路桥梁承载能力评估目标可靠指标计算[J]. 世界桥梁, 2013, 41(3): 73-76 YOU Ji, FANG Tao, FU Gong-kang. Calculation of Targeting Reliability Index for Bearing Capacity Evaluation of Highway Bridges in China[J]. World Bridges, 2013, 41(3): 73-76 |
| [8] | MOSES F. Bridge Evaluation Based on Reliability[C]//Structural Reliability in Bridge Engineering: Design, Inspection, Assessment, Rehabilitation and Management. New York: McGraw-Hill, 1996: 42-53. |
| [9] | ISO 2394—2015, General principles on Reliability for Structures[S]. |
| [10] | AASHTO. Guide Manual for Condition Evaluation and load and Resistance Factor Rating of Highway Bridges (LRFR)[M]. Washington, D.C.: AASHTO, 2003. |
| [11] | GB50153—1999, 工程结构可靠性设计统一标准[S]. GB50153—2008, Unified Design Standard for Reliability of Engineering Structures[S]. |
| [12] | 张喜刚. 公路桥梁汽车荷载标准研究[M]. 北京: 人民交通出版社, 2014. ZHANG Xi-gang. Research on Vehicle Load Standard of Highway Bridges[M]. Beijing: China Communications Press, 2014. |
| [13] | JTG/T J21—2011, 公路桥梁承载能力检测评定规程[S]. TG/T J21—2011, Specification for Inspection and Evaluation of Load-bearing Capacity of Highway Bridge [S]. |
 2017, Vol. 34
2017, Vol. 34
