扩展功能
文章信息
- 李勇, 张劲泉, 余波
- LI Yong, ZHANG Jin-quan, YU Bo
- 钢筋混凝土T梁旧桥极限承载能力研究
- Study on Ultimate Bearing Capacity of an Existing RC T-girder Bridge
- 公路交通科技, 2017, 34(4): 66-71
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(4): 66-71
- 10.3969/j.issn.1002-0268.2017.04.010
-
文章历史
- 收稿日期: 2016-09-07
2. 交通运输部公路科学研究院, 北京 100088
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
桥梁在设计时,只需满足设计荷载要求下的正常运营及极限承载能力即可,然而实际桥梁在运营过程中仍然会发生垮塌事故,这其中固然有汽车超载的原因,但是同时也显示出对于桥梁尤其是营运多年的桥梁极限承载能力的认识不足。
目前对于旧桥极限承载力评定一般会通过弹性有限元模型分析、特殊检测和荷载试验相结合的方式来判定[1],而有限元模型在计算时很难反映实际运营桥梁的材料特性,特殊检测通过检测桥梁的多种物理参数特性来评定,荷载试验也一般仅限于评定运营桥梁的正常使用状态。而对于运营桥梁极限承载能力的研究,最直接的办法就是通过实桥破坏试验来判定,但破坏性试验的成本相对较高,且一般为即将拆除的桥梁才有可能进行此类试验。尽管如此,且国内外学者已开展了一定数量的不同桥型单个桥梁的旧桥破坏性试验[2-7]来得到真实承载能力,认为旧桥的承载能力一般均远大于常规检测评定的桥梁承载能力。
铰接T型梁桥是公路桥梁较为常用的桥型,在中国20世纪70年代以后发展较多。但是,随着桥梁的运营过程中交通量的不断增加,桥梁负荷日益加重,在长期运营过程中桥梁又受到环境侵蚀或超载作用的影响,此类型桥梁出现了一些通用的病害现象,如裂缝发展严重、横隔板破坏严重等,使得了解和预测此类桥梁在超载条件下的结构状态 (特别是桥梁的极限状态) 变得日益重要。
本文以一座典型钢筋混凝土铰接T梁旧桥为例,通过外观检测、荷载试验以及破坏试验分别得到了此桥的极限承载能力,从而为此类型旧桥的加固或提载设计提供一定的参考。
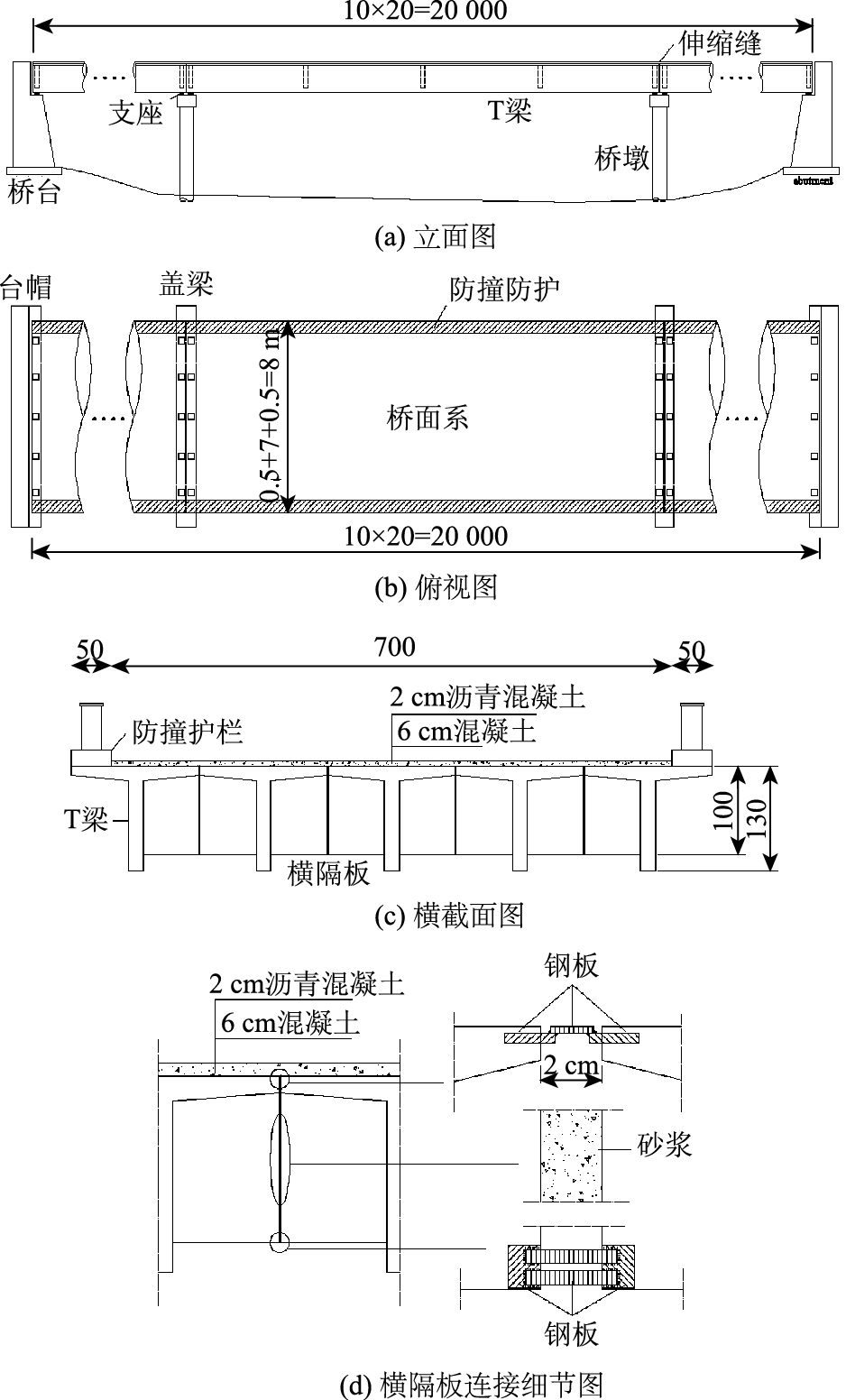
1 工程概况 1.1 桥梁概况本桥为10跨简支梁桥,单跨跨径20 m。桥面铺装连续,每跨横桥向由5片预制T梁拼接而成,桥型结构及构造如图 1所示。此桥建成于1982年,设计荷载为汽车-20级,设计车道为往返2车道。国内钢筋混凝土铰接T梁旧桥的数量较多,且病害发展较为严重。
|
| 图 1 全桥整体布置图 (单位:cm) Fig. 1 Layout of the whole bridge (unit:cm) |
| |
1.2 外观检测评定
本桥的下部结构及支座基本完好,但是上部结构外观状况较差,主要病害在桥面纵桥向沿T梁翼缘交接位置出现开裂、错位;T梁腹板出现较多竖向裂缝,且靠近支座处有斜向裂缝,且很多裂缝宽度均超过0.2 mm;T梁间横隔板破坏严重,部分横隔板连接处的灌注砂浆脱落或者开裂,且连接钢板锈蚀、焊缝开裂,如图 2所示;桥面沿T梁间纵向接缝出现较大的裂缝及竖向变形差。

|
| 图 2 典型桥梁病害 Fig. 2 Typical diseases of bridge |
| |
本桥综合评定为四类桥,应对此T型梁桥进行大修或改造。由于外观检查只能给出定性的结论,认为此桥的既有病害不满足正常运营的条件,但无法判定此桥的极限承载力是否满足设计荷载要求。
2 基于外观检测和特殊检测的极限承载能力评定既有配筋混凝土桥梁的极限承载能力进行鉴定,主要通过以下公式[1, 8]:
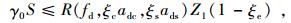
|
(1) |
式中,γ0为结构的重要性系数;S为荷载效应函数;R(·) 为抗力效应函数;fd为材料强度设计值;adc为构件混凝土几何参数值;ads为构件钢筋几何参数值;Z1为承载能力检算系数;ξe为承载能力恶化系数;ξc为配筋混凝土结构的截面折减系数;ξs为钢筋的截面折减系数。
由于主梁混凝土材料较为离散,且本桥运营时间较长,所以采用钻芯法对混凝土强度测试,试件个数为10个,直径和高度均为100 mm,得到混凝土立方体抗压强度推定值[9]范围为47.2~58.8 MPa,平均值50.33 MPa,标准差3.748 MPa,进而推得混凝土弹性模量为33 650 MPa,轴心抗压强度标准值和设计值分别为30.6 MPa和21.2 MPa,明显高于原设计混凝土强度 (抗压强度标准值和设计值分别为21.5 MPa和17.5 MPa)。由于本桥进行了破坏试验,破坏时间结束后选择其中的节段钢筋进行测试,其中主筋钢筋弹性模量取值为2.08×105 MPa,抗拉设计强度值为376 MPa;箍筋弹性模量取值为2.12×105 MPa,抗拉设计强度值为243 MPa。
综合缺损状况、混凝土强度和自振频率的评定结果,可以得到评定的Z1值为1.02。主梁几何尺寸及内部钢筋尺寸测量结果与设计尺寸基本相同;混凝土材料表面存在微风化现象,对混凝土进行碳化深度测试有略微碳化,所以主梁的混凝土截面折减系数ξc最终取为0.98;钢筋无露筋现象,但是由于主梁存在大量裂缝,且内部纵筋有轻微锈蚀现象,所以钢筋截面折减系数ξs取值为0.95。承载能力恶化系数ξe取值为0.079 6。根据确定的对应交通量、大吨位车辆混入率、轴荷分布的活载影响修正系数,计算汽车检算荷载的活载影响修正系数ξq为1.116。
在进行承载力分析时,对于主梁的抗弯极限承载能力,未考虑混凝土桥面铺装参与受力,仅将其作为恒荷载施加在结构上。这种T梁结构类型在计算跨中最不利弯矩时,符合Guyan-Massonnet桥梁空间理论。在1.2倍恒载和1.4倍移动荷载组合作用下,单根T梁最不利弯矩效应为2 131.9 kN·m。若根据原设计混凝土和钢筋的相关参数,并考虑T梁受拉区的主筋 (10ϕ28) 以及受拉区的架立筋 (2ϕ22),计算的抗力效应为2 187.4 kN·m,根据式 (1),得到的单根T梁抗力设计值为2 053.5 kN·m,则判定此桥的极限承载能力不满足原设计要求。若以混凝土的实测强度标准值进行分析,并考虑相应的钢筋后,则单根T梁的实际承载力应为2 750 kN·m,根据式 (1),单根T梁抗力评定值为2 590 kN·m,此桥的实际极限承载能力满足设计运营荷载的要求。
与外观检查对桥梁使用的定性评价不同,特殊检查给出了桥梁实际承载力定量评价。尽管桥梁从外观现状看起来很差,而极限承载力却只降低了5%左右。
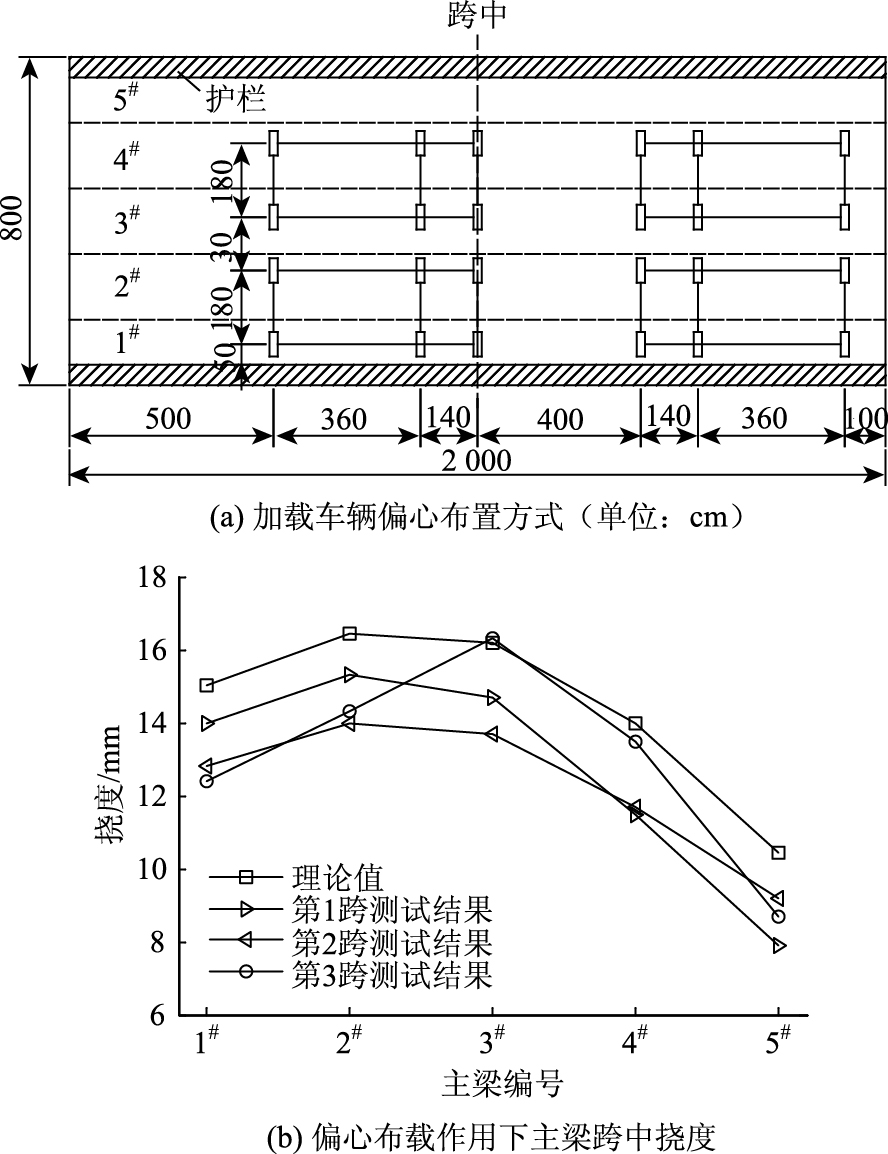
3 基于静力荷载试验的极限承载能力评定静力荷载试验是在桥梁定期检测中常用的检测手段,可以获得主梁在试验荷载作用下控制截面的应变、位移和裂缝的变化规律,主要用以评价桥梁的正常使用极限状态。若进行了静力荷载试验,则式 (1) 中的Z1可以用Z2代替[1],其中Z2的值由校验系数结果来决定。本次静力荷载试验主要通过4辆重约300 kN的加载车按照图 3(a)进行加载,主要检验主梁跨中截面在最不利偏心布载作用下产生的正弯矩效应及竖向挠度是否满足规范要求,见图 3(b)。试验跨选择第1跨、第2跨和第3跨,其中第3跨为破坏试验跨。
|
| 图 3 静力荷载试验 Fig. 3 Static loading test |
| |
试验布载下各片T梁跨中挠度的实测结果与理论计算结果的比值为校验系数η,则第1跨至第3跨的校验系数范围分别为0.76~0.95, 0.81~0.98和0.76~1.01。有限元模型虽未考虑裂缝带来的刚度折减,但通过校验系数可知,实测挠度结果仍比计算值偏低,说明本桥实际是满足设计荷载的正常运营。
通过荷载试验可知,第3跨3#梁挠度分配较前两跨大13%,而在对T梁特殊检测时也发现,此梁跨中横隔板开裂严重,说明第3跨3#梁由于横隔板的损坏,刚度有所降低,另外两跨横隔板虽然有不同程度的破损,但尚可满足横向联系的作用。
通过荷载试验的校验系数可得到校验系数Z2,进而对结构的极限承载能力进行评定,由于校验系数最大值为1.01,且为病害较为严重的第3跨,查得Z2取值可为0.95,使用Z2代替公式中的Z1,则可以对桥梁的极限承载能力进行进一步评定,若按照原设计混凝土强度进行计算,可以得到T梁的抗力评定为1 912.6 kN·m,判定本桥的极限承载能力不满足设计要求。若根据实测混凝土强度进行计算,则实际抗力为2 412 kN·m,仍可判定本桥极限承载能力满足设计要求。
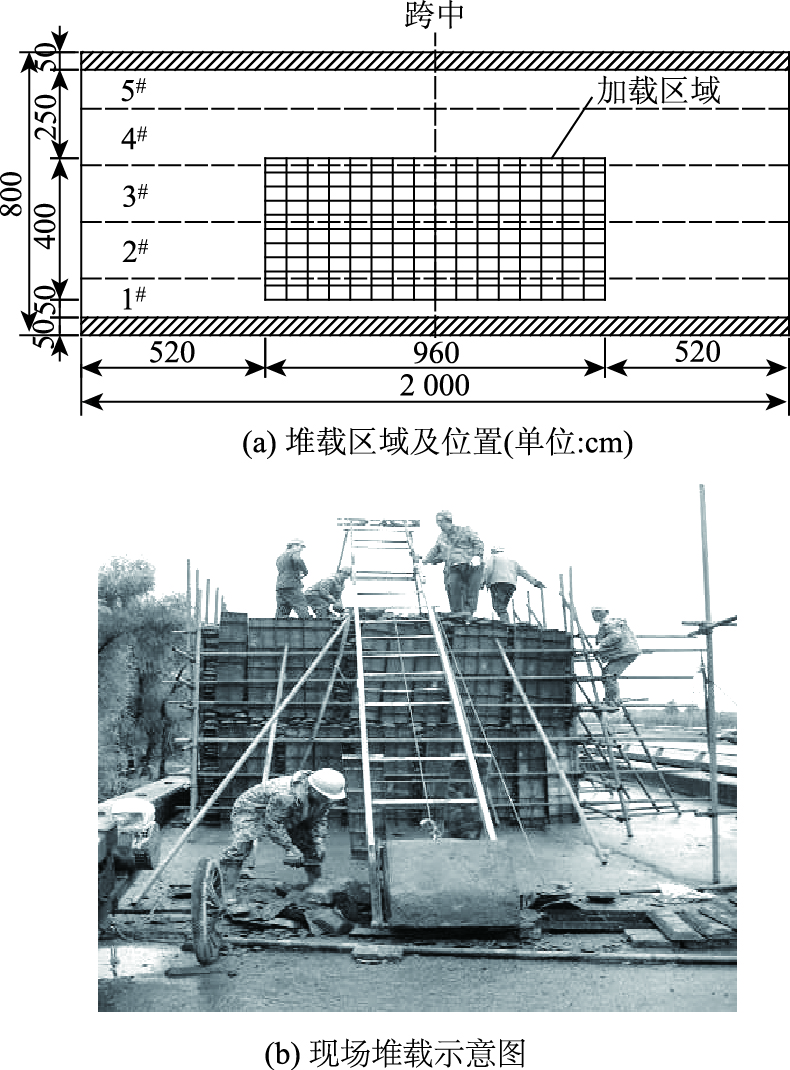
4 基于破坏试验的极限承载能力测试鉴于此桥第3跨T梁病害较为严重,对结构的耐久性影响较大,需要更换主梁,所以对此跨进行了实桥破坏试验,从而测得此桥跨真实的极限承载力。试验选用配重铁砖进行偏心堆载,加载时将加载铁块通过分级加载堆放于加载箱体内。堆载区域为一矩形面积,堆载区域沿顺桥向长9.6 m,沿横桥向宽4 m,堆载面距路缘石0.5 m,如图 4所示。
|
| 图 4 破坏加载试验 Fig. 4 Destructive loading test |
| |
当堆载达到约4 400 kN时,T梁跨中腹板出现了大量裂缝宽度大于2 mm的U形贯通裂缝,边T梁跨中挠度达到12 cm,约为计算跨度的1/50,且主梁下挠速度增快。此时,1/4跨、跨中和3/4跨处的横隔板完全破坏,砂浆完全开裂或脱落,连接钢板完全断裂,横隔板变形呈八字形。
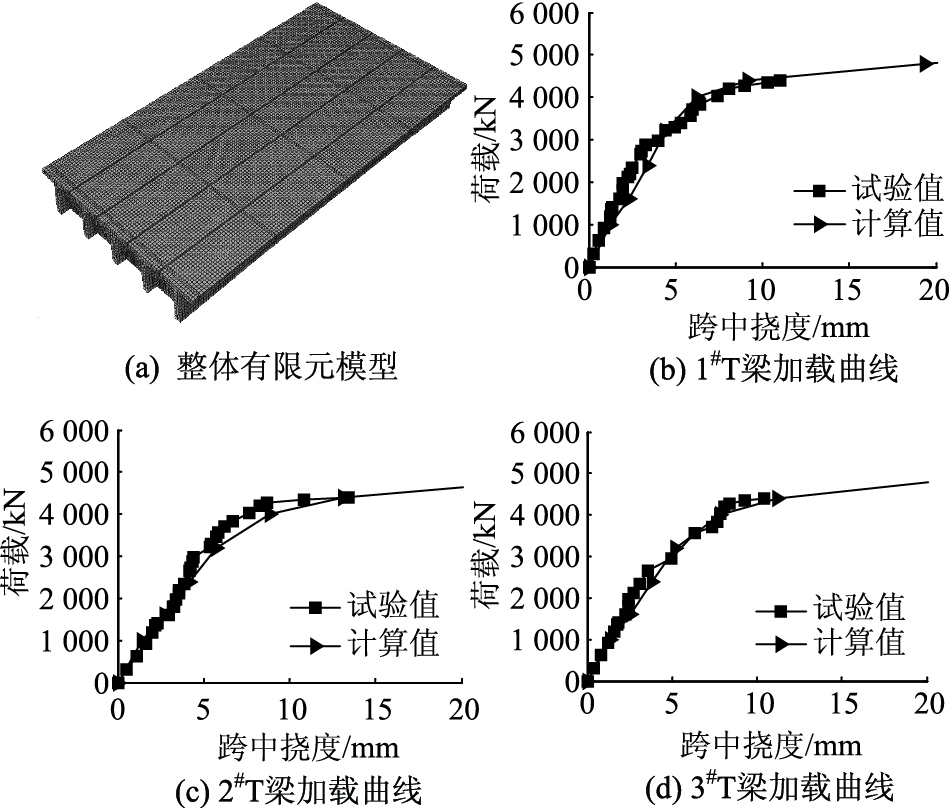
基于ABAQUS软件建立了实桥空间精细化有限元模型,见图 5。本模型考虑了混凝土铺装层参与受力,并假设混凝土铺装与主体梁结构结合良好,经检测防撞护栏由于与T梁有脱裂现象,不参与结构受力。混凝土采用实体单元模拟,见图 5。钢筋采用桁架单元模拟,钢筋通过嵌入混凝土参与受力。其中,钢筋考虑了箍筋、主筋受拉筋、构造钢筋如分布筋、受压筋等均参与受力分析。
|
| 图 5 有限元模型, 计算结果与试验结果对比 Fig. 5 FE model and comparison between test result and calculation result |
| |
模型中主要材料为素混凝土和普通钢筋。混凝土采用塑性损伤本构模型,钢筋采用理想弹塑性本构模型[10-11]。
由图 5可知,有限元模型计算结果与破坏试验实测结果符合得较好,从计算结果可知,实桥在加载终止时仍尚未达到桥梁的极限承载能力,延性较好。
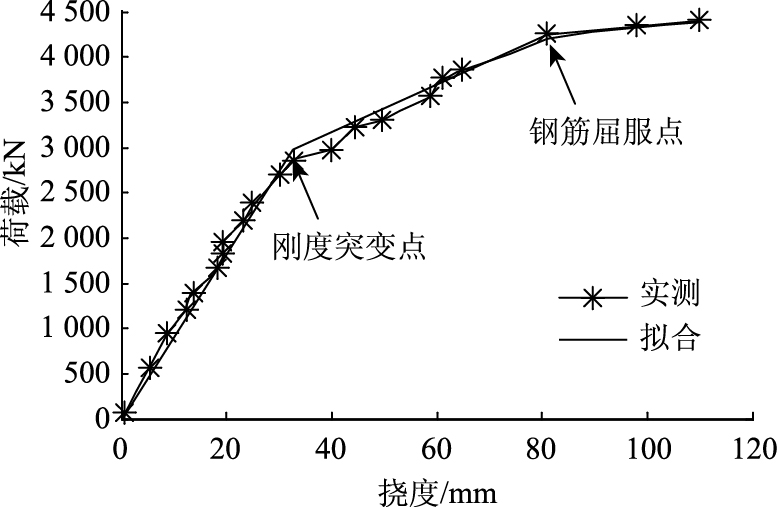
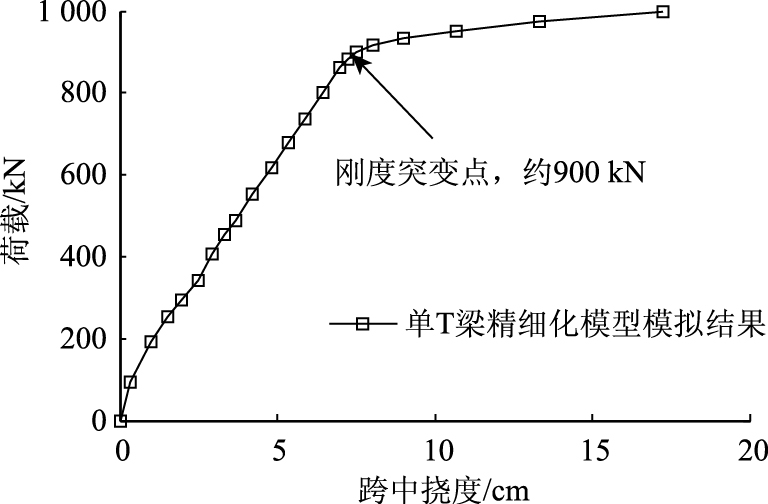
5 极限承载力试验结果对比通过对1#梁的实测荷载-挠度曲线进行分析,可知其刚度突变点对应加载吨位为2 800 kN,钢筋屈服点对应加载吨位为4 200 kN,如图 6所示。若定义钢筋屈服对应的荷载为最不利极限荷载,则根据横向分布系数,1#T梁分担的荷载约为900 kN,这与单T梁精细化三维有限元模型的极限承载能力模拟结果较为接近,如图 7所示。
|
| 图 6 1#T梁荷载-挠度曲线分段拟合 Fig. 6 Multi-phase fitting of load-deflection curve of T-girder No. 1 |
| |
|
| 图 7 单T梁精细化模型计算结果 Fig. 7 Computation result of single T-girder by fine model |
| |
根据破坏试验得到的1#T梁的荷载分担量,再叠加T梁的自重效应,得到1#T梁跨中弯矩抗力应为4 046 kN·m,大于理论计算值,这与既有破坏试验研究结论较为相似[4-6, 12]。其原因为实桥破坏性试验加载过程中,当1#T梁接近屈服时,由于横隔板及桥面铺装层的存在,一部分荷载由其他T梁进行承担,延缓了1#T梁的屈服,荷载可进一步增加,当1#T梁真正屈服时,由于其他T梁的承担,荷载已超过单梁设计屈服荷载,因此以实桥实际屈服荷载反推出来的单梁极限弯矩必定高于单T梁按理论计算得到的极限弯矩,即对于装配式T梁桥而言,只有当受力较大的T梁都发生屈服时才会发生倒塌。
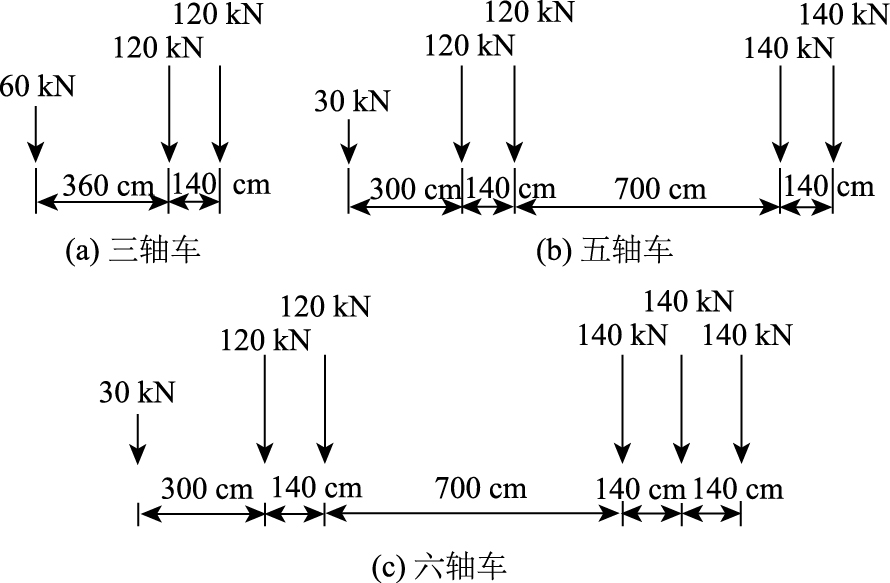
表 1给出了不同试验方法得到的本桥极限承载能力评定值,并与设计荷载进行对比,其中设计荷载组合为1.2倍恒荷载加1.4倍汽车荷载,汽车荷载分别采用300 kN三轴标准车车队、500 kN五轴标准车车队及690 kN六轴标准车车队 (见图 8),按照两车道最不利偏心布载,按照本桥实测材料参数进行理论计算并根据特检、荷载试验分别进行承载能力评定,本桥极限承载能力尚能满足三轴车和五轴车的运营要求,但是六轴车不能正常通行,实桥破坏试验证明了本桥实际上依然满足3种标准车的正常通行,且尚具有一定的超载能力。若根据实际破坏试验得到的极限承载能力,则可以判定本桥实际通行的三轴车、五轴车及六轴车队分别不能超过1 026,1 610 kN和1 800 kN,否则会导致本桥发生垮塌事故。综合前述外观检测可知,虽然本桥具有较为严重的典型病害,但其实际极限承载力尚能满足实际车辆的运营要求。按照现行规范对旧桥进行承载能力评定具有一定的安全可靠度。
| 评定方法 | 极限承载力/(kN·m) | 安全系数 | ||
| 荷载组合1 | 荷载组合2 | 荷载组合3 | ||
| 理论计算 | 2 750 | 1.19 | 1.14 | 1.01 |
| 特殊检测评定 | 2 590 | 1.13 | 1.08 | 0.95 |
| 荷载试验评定 | 2 412 | 1.05 | 1.00 | 0.88 |
| 破坏试验评定 | 4 046 | 1.76 | 1.68 | 1.48 |
| 注:荷载组合1为1.2×恒载+1.4×三轴车车队,2 302 kN·m;载荷组合2为1.2×恒载+1.4×五轴车车队,2 402 kN·m; 荷载组合3为1.2×恒载+1.4×六轴车车队,2 735 kN·m。 | ||||
|
| 图 8 不同载重标准车 Fig. 8 Trucks with different weight |
| |
6 结论
通过对一座运营多年钢筋混凝土铰接T梁旧桥按照常规的检测方式进行极限承载能力评定,并与破坏试验得到的实际承载能力进行对比可知,尽管此类T梁桥运营多年,且具有典型病害,开裂现象显著,但是通过实桥破坏试验得到的真实极限承载力远大于理论计算值及常规试验评定值,根据现行承载能力评定规范,通过特殊检测以及荷载试验评定的极限承载力均基于对理论计算值进行折减,安全可靠度较高,可为此类钢筋混凝土铰接T梁旧桥的加固与养护提供一定的技术参考。
| [1] | JTG/T J21—2011, 公路桥梁承载能力检测评定规程[S]. JTG/T J21—2011, Specification for Inspection and Evaluation of Load-bearing Capacity of Highway Bridge[S]. |
| [2] | AZIZINAMINI A. Full Scale Testing of Old Steel Truss Bridge[J]. Journal of Constructional Steel Research, 2002, 58(5): 843-858 |
| [3] | MILLER R A, AKTAN A E, SHAHROOZ B M. Destructive Testing of Decommissioned Concrete Slab Bridge[J]. Journal of Structural Engineering, 1994, 120(7): 2176-2198 |
| [4] | 张健飞, 张宇峰. 预应力混凝土连续箱梁桥破坏性试验研究[J]. 公路交通科技, 2008, 25(10): 63-68 ZHANG Jian-fei, ZHANG Yu-feng. Study on Destructive Experiment of Prestressed Concrete Continuous Box Girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2008, 25(10): 63-68 |
| [5] | 徐文平. 既有预应力混凝土梁桥承载能力实桥试验及分析研究[D]. 南京: 东南大学, 2006. XU Wen-ping. Experimental Research and Analysis on Load Bearing Capacity of Existing Prestressed Concrete Girder Bridges[D]. Nanjing: Souhteast University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10286-2007030320.htm |
| [6] | 张建仁, 彭晖, 张克波, 等. 锈蚀钢筋混凝土旧桥超限及极限荷载作用的现场破坏性试验研究[J]. 工程力学, 2009, 26(增2): 213-224 ZHANG Jian-ren, PENG Hui, ZHANG Ke-bo, et al. Test Study on Overload and Ultimate Behavior of Old Reinforced Concrete Bridge Through Destructive Test of Corroded Bridge[J]. Engineering Mechanics, 2009, 26(S2): 213-224 |
| [7] | 余波, 李勇, 孙晓红, 等. 左家堡大桥实桥承载力破坏试验及分析[J]. 公路交通科技, 2011, 28(7): 100-105 YU Bo, LI Yong, SUN Xiao-hong, et al. Destructive Test and Analysis of Bearing Capacity of Zuojiabao Bridge[J]. Journal of Highway and Transportation Research and Development, 2011, 28(7): 100-105 |
| [8] | 张劲泉, 冷艳玲, 李万恒, 等. 中国公路桥梁承载能力评定规程的可靠性水准[J]. 公路交通科技, 2015, 32(4): 59-63, 77 ZHANG Jin-quan, LENG Yan-ling, LI Wan-heng, et al. Reliability Level of Load-bearing Capacity Evaluation Specification of Highway Bridges in China[J]. Journal of Highway and Transportation Research and Development, 2015, 32(4): 59-63, 77 |
| [9] | CECS 03: 2007, 钻芯法检测混凝土强度技术规程[S]. CECS 03:2007, Technical Specification for Testing Concrete Strength by Drilling Core Method [S]. |
| [10] | SHAHROOZ B M, HO I K, AKTAN A E, et al. Nonlinear Finite Element Analysis of Deteriorated RC Slab Bridge[J]. Journal of Structural Engineering, 1994, 120(2): 422-440 |
| [11] | SONG H W, YOU D W, BYUN K J, et al. Finite Element Failure Analysis of Reinforced Concrete T-girder Bridges[J]. Engineering Structures, 2002(24): 151-162 |
| [12] | HO I, SHAHROOZ B M. Finite Element Modeling of a Deteriorated R.C. Slab Bridge: Lessons Learned and Recommendation[J]. Structural Engineering and Mechanics, 1998, 6(3): 259-274 |
 2017, Vol. 34
2017, Vol. 34
