扩展功能
文章信息
- 王骁帆, 应正兵, 刘朝晖, 苏颖奇, 李盛
- WANG Xiao-fan, YING Zheng-bing, LIU Zhao-hui, SU Ying-qi, LI Sheng
- 温度场对连续配筋混凝土路面纵向配筋的影响
- Effect of Temperature Field on Longitudinal Reinforcement of Continuously Reinforced Concrete Pavement
- 公路交通科技, 2017, 34(4): 16-24, 57
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(4): 16-24, 57
- 10.3969/j.issn.1002-0268.2017.04.003
-
文章历史
- 收稿日期: 2016-05-03
2. 长沙理工大学 公路养护技术国家工程实验室, 湖南 长沙 410004
2. State Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science and Technology, Changsha Hunan 410004, China
连续配筋混凝土路面 (CRCP) 由于配置了纵向钢筋,具有结构强度高、使用寿命长和行车舒适度高等特点,符合长寿命重载交通的发展趋势[1-2]。CRCP的配筋设计主要考虑最大温差引起的温缩应力和温度梯度引起的翘曲应力的影响[3-4]。配筋设计的3个指标 (横向裂缝宽度、缝隙间距、钢筋拉应力) 均与温度场直接相关。但是,现行规范的配筋设计对温度场的考虑不够全面。钢筋埋深处的年最大温差 (ΔTζ) 取一年中最热月份日最高气温和最冷月份日最低气温的月平均值之差,未考虑面板厚度和配筋位置对ΔTζ的影响[5]。温度梯度与路面结构材料的关系也不明确,不利于纵向配筋的设计和施工质量控制。
CRCP的热量主要来自于导流热、对流热和辐射热。严作人和Barbr用余弦三角级数描述了太阳辐射对路面的周期性影响,并用扩大气温振幅的方法来考虑有效辐射[6]。埃·牛顿用两个正弦函数来描述大气温度的日变化[6]。温度场的求解主要有现场实测和理论计算两种方法:前者通过实测路面不同结构层的温度,以回归分析法得到温度场随时间的变化规律[7-8];后者通过差分法和有限元法求解热传导微分方程[9-10]。Pretorius和Christison用有限差分法和有限元法,对半无限弹性层状体系的温度场进行了分析[6-8]。严作人在Pretorius的基础上,从定性与定量的角度,分析了基层材料的热力学性质对温度场的影响规律[6]。谈至明分析了温度场线性分布假设所带来的计算误差[11],他还对水泥混凝土路面温度的日变化进行了实测和拟合[7]。Nishizawa对CRCP的温度场进行了实测,对温缩应力与温度翘曲应力进行了研究[12]。董侨和顾兴宇对复合式路面的温度分布、温度梯度和变温速率进行了数值分析[13-14]。但是,关于CRCP温度场数值分析的研究还不够全面。基于实测的研究方法较难确定板厚、钢筋埋深和面板材料对ΔTζ和温度梯度的影响规律。
文章围绕以上不足,利用ABAQUS软件进行了针对性的数值计算。研究成果可以指导CRCP的配筋设计,也可以为路面施工质量控制提供参考。
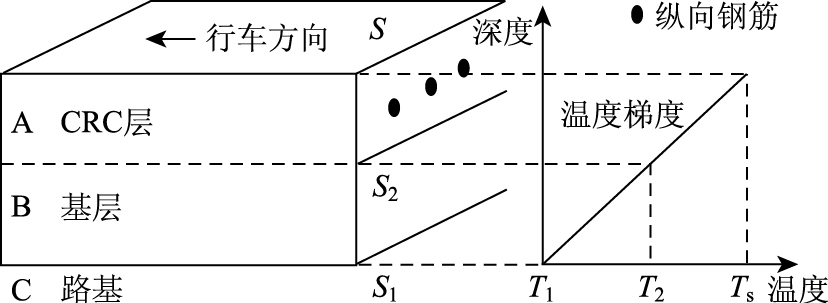
1 CRCP的热弹性理论 1.1 计算模型CRCP的三维计算结构如图 1所示。S为上表面,对应温度Ts;S1为CRC层与基层之间的接触界面,对应温度T1;S2为基层和路基之间的接触界面,对应温度T2。取深度方向为z轴,行车方向为x轴,路面横向为y轴。
|
| 图 1 CRCP的计算模型 Fig. 1 CRCP calculation model |
| |
1.2 辐射与热流条件
(1) 导热交换
导热交换主要是指结构层内部的热能交换。根据傅里叶热传导基本定律,热能传递方向与温度梯度方向相反,热流密度q与温度梯度的大小成正比:
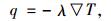
|
(1) |
式中,∇为哈密顿算子;λ为导热系数,水泥混凝土取1.4~2.3 W/(m2·℃)。
(2) 对流换热
对流换热指由板面和环境温差引起的热能交换,埃·牛顿[6-11]提出了对流换热密度qh的冷却方程:

|
(2) |
式中,hc为对流放热系数,高低温季节分别取19 W/(m2·℃) 和23 W/(m2·℃);Ts为板面温度;Ta为环境温度。
潭耒高速公路位于公路区划Ⅳ区。文章参考文献[15]的做法,用某地7月和12月的24 h代表性气温,作为该月各时刻的温度平均值 (ΔTζ=64 ℃),研究温度场对CRCP配筋设计指标的影响。表 1数据主要用于定义CRCP的升温幅值曲线。
| 时刻 | 气温/℃ | |
| 7月 | 12月 | |
| 00:00 | 32.60 | -13.90 |
| 01:00 | 31.32 | -15.98 |
| 02:00 | 30.11 | -18.12 |
| 03:00 | 29.55 | -19.06 |
| 04:00 | 29.02 | -20.01 |
| 05:00 | 29.68 | -18.82 |
| 06:00 | 30.41 | -17.61 |
| 07:00 | 32.26 | -14.20 |
| 08:00 | 34.00 | -10.78 |
| 09:00 | 36.53 | -6.54 |
| 10:00 | 38.94 | -2.23 |
| 11:00 | 40.75 | 1.22 |
| 12:00 | 42.54 | 4.56 |
| 13:00 | 43.30 | 5.81 |
| 14:00 | 44.00 | 6.96 |
| 15:00 | 43.44 | 6.06 |
| 16:00 | 42.91 | 5.10 |
| 17:00 | 41.72 | 2.91 |
| 18:00 | 40.47 | 0.83 |
| 19:00 | 39.16 | -1.63 |
| 20:00 | 37.77 | -4.14 |
| 21:00 | 36.54 | -6.48 |
| 22:00 | 35.23 | -9.13 |
| 23:00 | 33.86 | -11.34 |
严作人用两个不同周期的正弦波函数的组合曲线[6-11]来近似比拟气温的周期性变化:
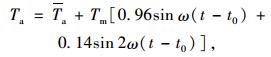
|
(3) |
式中,t为时间;ω为地球自转角频率;t0为初相位,取9 h;Tm为气温日变化幅值;Ta为日均气温。
(3) 太阳辐射
太阳短波辐射是CRCP的重要热能来源。表 2为公路区划Ⅳ区某地的气象数据,面板单位面积上吸收的太阳辐射能qs为:
| 计算参数 | 日太阳辐射量/(MJ·m-2) | 日照时长/h | 风速/(m·s-1) |
| 高温季节 | 26.0 | 12.0 | 2.6 |
| 低温季节 | 1.61 | 10.2 | 3.6 |
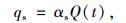
|
(4) |
式中,αs为吸收系数,取0.62;Q为太阳辐射能密度。
Q是关于t的周期性分段函数[6-11]。从日出到正午,Q随时间递增;从正午到日落,Q随时间递减;晚上Q为0。为了得到连续光滑的辐射曲线,将Q函数展开成傅里叶级数形式:
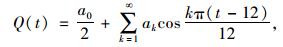
|
(5) |
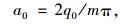
|
(6) |
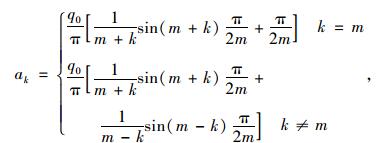
|
(7) |
式中,q0=1.31×10-2mQs, m=12/u, Qs为单位面积的日太阳辐射总量, u为日照时长;k为阶数 (k越大,函数的级数展开式与原函数的差值越小),经过子程序调试,k取40可以使计算误差小到忽略。
(4) 路表有效辐射
路表有效辐射指面板释放的长波辐射能与吸收的逆长波辐射能的差值。根据斯特藩-玻尔兹曼定律,面板单位面积的有效辐射能qF为:
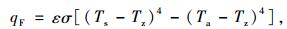
|
(8) |
式中,ε为黑度,水泥混凝土路面取0.88;σ为斯特藩-玻尔兹曼辐射系数,取5.669 7×10-8 W/(m2·K4);Tz为绝对零度,取-273 ℃。
因此,CRCP内部存在热能交换;板面的热流则由辐射热 (包括太阳辐射和路表有效辐射) 和对流热组成,即q=qh+qs+qF。
1.3 热传导微分方程(1) 热传导微分方程
CRCP的热传导微分方程为:
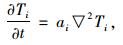
|
(9) |
式中,ai为i层的当量热扩散率,ai=λi/(Ci·ρi);λi为i层的导热系数;Ci为i层材料的比热容;ρi为i层材料的密度;Ti为i层的温度。
(2) 温度场的边值条件
假设CRCP各结构层间接触紧密,接触面S1的温度和法向热流密度qn完全连续:
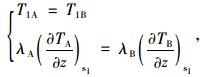
|
(10) |
路表的诺依曼边界条件为:
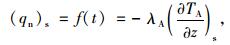
|
(11) |
式中,T1A为S1上表面温度;T1B为S1下表面温度;TA为CRC层的温度;TB为基层温度;λA为CRC层的导热系数;λB为基层的导热系数。
对于不稳定温度场,初始温度对温度场的影响随着时间变得越来越小。由于无法实测路面初始温度,取4 d的计算周期。
(3) 热传导微分方程的求解
对于平面问题,工程数学[16]采用差分法和有限元法求解热传导微分方程;对于空间问题,只能采用有限元法。CRCP路面为三维结构模型,温度场采用有限元法求解。
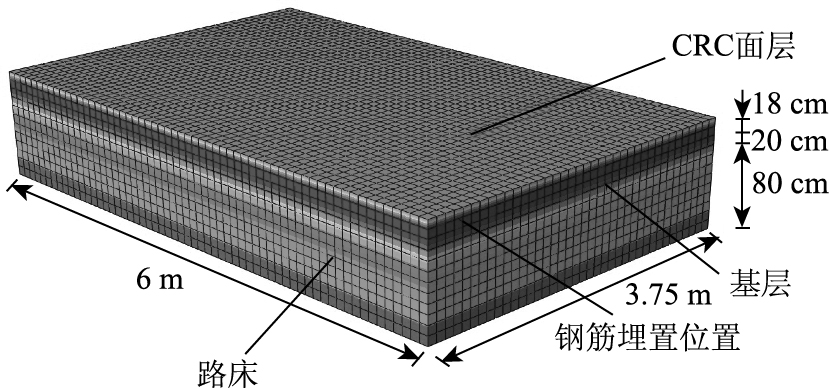
2 CRCP温度场的计算 2.1 有限元模型的建立CRCP的结构和材料取自潭耒高速公路[17],分析结构则采用三维有限元模型, 见图 2。
|
| 图 2 CRCP有限元模型 Fig. 2 CRCP FE model |
| |
(1) 材料的热力学参数
各结构层的热力学参数如表 3所示。钢筋网布置在CRC板中位置,采用HRB335。纵向钢筋的直径ds为16 mm,配筋率ρ≈0.9%,间距取124 mm,横向共30根。
| 路面结构 | 混凝土 | 纵筋 | 基层 | 路床 |
| 密度/(kg·m-3) | 2 400 | 7 800 | 2 100 | 1 800 |
| 热传导率/[J·(m·h·℃)-1] | 6 300 | 125 640 | 5 616 | 5 500 |
| 比热容/[J·(kg·℃)-1] | 973 | 520 | 912 | 1 040 |
| 厚度/m | 0.18 | — | 0.2 | 0.8 |
| 长度/m | 6 | 6 | 6 | 6 |
| 宽度/m | 3.75 | ϕ16 | 3.75 | 3.75 |
(2) 单元和网格划分
路面的单元类型采用DC3D8(八节点线性传热实体单元);钢筋在赋予截面面积和材料属性后,利用Embedded工具在建好的水泥混凝土板中嵌入钢筋骨架,单元类型采用DC1D2(二节点传热杆单元)[18-19]。
网格的划分对计算结果影响较大,经过调试与对比,在种子定义和网格尺寸取值时,取CRC板为0.1 m,基层为0.1 m,钢筋为0.05 m,路基为0.1 m,共计30 960个网格。
(3) 板面辐射和热流的模拟
分别进行高温、低温季节的瞬态、稳态热分析。为了实现路面内部的连续导热,建模时,对路基路面采用整体式模型的剖分技术;对钢筋则采用植入单元技术[20]。对流换热用Interaction模块的Surface film condition定义。根据表 1、表 2和式 (2)~(3) 的参数,用子程序FILM定义板面24 h的周期性温度变化和热能交换,以实现对qh的模拟。太阳辐射用Load模块的Surface heat flux功能定义。根据表 2和式 (4)~(7) 的参数,用子程序DFLUX定义CRCP板面对太阳辐射的吸收,从而实现qs随t的变化规律。路表有效辐射用Interaction模块的Surface radiation功能定义。根据表 1的气温数据绘制Amplitude变温曲线,结合式 (8) 的参数,以实现对qF的模拟。路床底部由于路基路面的保温作用,其日变化幅度很小,假设底面初始温度为20 ℃;假定CRCP只在板面散热,其他面默认为绝热面。
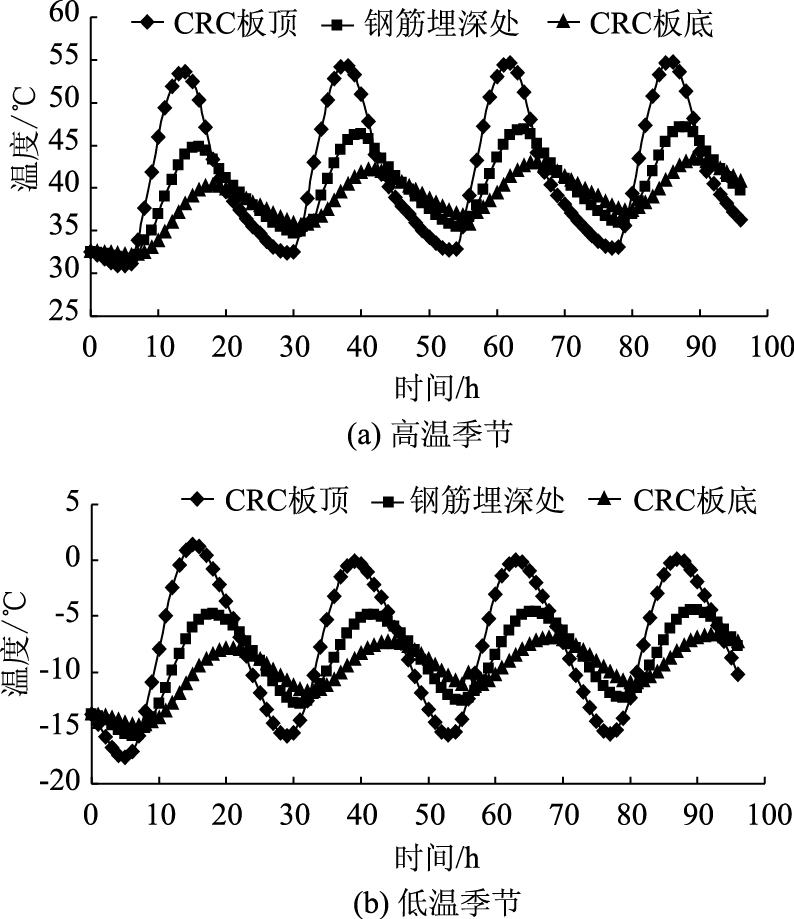
2.2 CRCP温度场分析经过4个周期 (96 h) 的计算,得到高、低温季节CRCP钢筋埋深位置较为稳定的温度场,见图 3。第4个周期温度沿深度方向的分布见图 4。
|
| 图 3 CRCP的温度场 (4个周期) Fig. 3 Temperature field of CRCP (4 cycles) |
| |
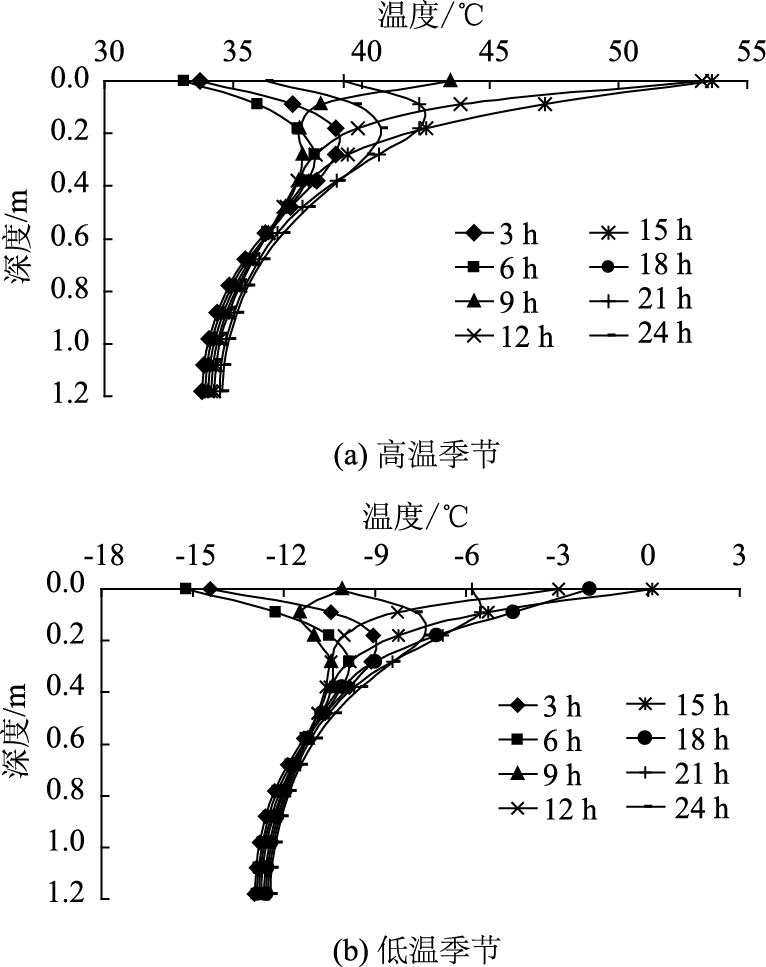
|
| 图 4 温度沿深度的分布 Fig. 4 Temperature profile through depth |
| |
由图 3可知:
(1) 钢筋埋深位置的温度曲线与大气温度曲线相比,周期相同但是振幅偏小。其相位相对于CRC板底面温度曲线要超前,相对于CRC板上表面温度曲线要滞后。
(2) 高温季节,钢筋埋置位置的温度场振幅不断增加并最终趋于稳定。这是因为高温季节,路面吸收的热量大于放出的热量,随着残余热量的积累,温度不断升高,最终趋近于环境温度;低温季节则正好相反。
(3) 高温季节,钢筋埋深位置的温度峰值出现在下午4:00,谷值出现在上午6:00;低温季节,钢筋埋深位置的温度峰值出现在下午6:00,谷值出现在上午7:00。
(4) 钢筋埋深位置的年最高温度为47.17 ℃,最低温度为-12.35 ℃。因此,ΔTζ应由64 ℃修正为59.53 ℃。这是由于钢筋上层的混凝土具有隔热作用。
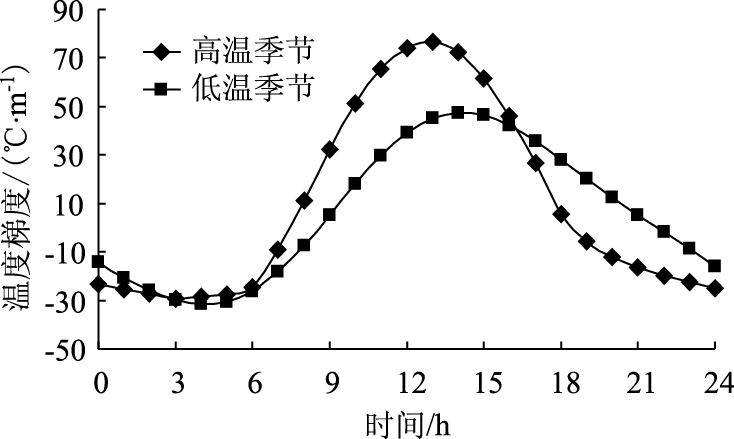
由图 4可知:CRCP面板由于厚度较薄 (0.18 m),其温度沿深度方向的分布呈线性。基层以下 (大约距板顶0.2 m) 呈现非线性。在路床深处,温度梯度则逐渐衰减为0。因此,当CRC板较薄时,温度梯度可近似取上下面温差与厚度的比值。绘制第4个周期CRCP面层温度梯度随时间变化关系如图 5所示。
|
| 图 5 CRCP面层的温度梯度 Fig. 5 Temperature gradient of surface layer of CRCP |
| |
由图 5可知:
(1) 正、负温度梯度均表现一定周期性。
(2) 高温季节,早上8:00到下午6:00,CRC板受正温度梯度的作用,在下午1:00达到最大正温度梯度76.48 ℃/m;其他时间受负温度梯度影响,在上午3:00达到最大负温度梯度-29.29 ℃/m。
(3) 低温季节,上午9:00到下午9:00受正温度梯度的影响,在下午2:00达到最大正温度梯度46.56 ℃/m;其他时间受负温度梯度影响,在上午4:00达到最大负温度梯度-31.55 ℃/m。
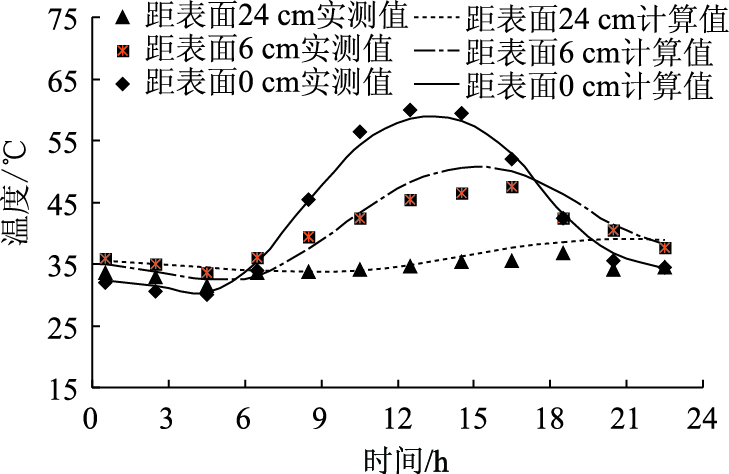
2.3 有限元计算的验证文献[14]对CRC+AC刚柔复合式路面的温度场进了实测和调研。文章用其实测温度验证有限元模型的合理性。验证模型采用的路面结构为:沥青混凝土 (AC) 层厚度10 cm;基层厚度40 cm;路床厚度80 cm。AC层的太阳辐射吸收系数αs取0.85,黑度ε取0.93。材料的热力学参数见相关文献[14]。建模的基本方法、边界条件和计算理论与本文一致。由于初始温度采用0点的实测温度。故无需考虑由于初始温度不同,对温度场计算带来的误差,进行有限元计算时只取1个周期 (24 h),结果如图 6所示。
|
| 图 6 有限元计算的验证 Fig. 6 Verification of FE calculation |
| |
由图 6可知:温度场的有限元计算值与实际测值的拟合程度较好。最大相对误差为3.7%,符合工程精度 (5%) 的要求。
3 纵向配筋温度参数的敏感性分析在进行敏感性分析时,模型基本参数同表 3和图 2。分析某个因素的敏感性时,采用简单对比试验,即基本参数保持不变,对该参数则赋予不同的取值水平。材料热力学性质的敏感性主要是混凝土的热传导率和比热容对温度参数 (包括温度梯度和最大温差) 的影响。
3.1 板厚对温度参数的影响CRC板的厚度分别取0.18,0.25,0.30,0.35 m和0.40 m,钢筋统一布置在距板顶0.10 m处。最大温度梯度与板厚的关系见图 7。
|
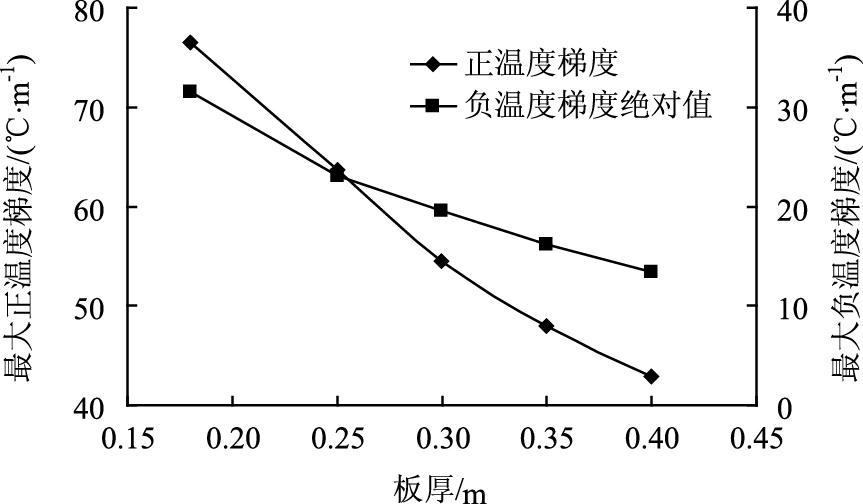
| 图 7 最大温度梯度与板厚的关系 Fig. 7 Relationship of maximum temperature gradient and slab thickness |
| |
经计算,CRC板厚每增加0.05 m,钢筋埋置位置的ΔTζ增加约0.03 ℃,板厚对ΔTζ的影响忽略不计。由图 7可知,板厚对温度梯度的影响较大,最大温度梯度随板厚的增加而减小。例如:当板厚由0.18 m变化到0.25 m时,最大正温度梯度减小了16.77%,最大负温度梯度减小了26.98%。
文献[1]取22 cm为标准厚度,提出了用温度梯度修正系数来考虑水泥混凝土板厚对最大正温度梯度的影响 (见表 4)。根据表 4,最大正温度梯度随板厚的变化趋势与图 7一致。例如:当板厚由0.18 m变化到0.25 m时,表 4最大正温度梯度减小了17.57%,图 7最大正温度梯度减小了16.77%。这也验证了有限元计算的合理性。
| 板厚/m | 0.18 | 0.20 | 0.22 | 0.24 | 0.26 |
| 修正系数 | 1.11 | 1.05 | 1.00 | 0.94 | 0.89 |
| 板厚/m | 0.28 | 0.30 | 0.32 | 0.34 | 0.36 |
| 修正系数 | 0.84 | 0.79 | 0.75 | 0.71 | 0.67 |
3.2 配筋位置对温度参数的影响
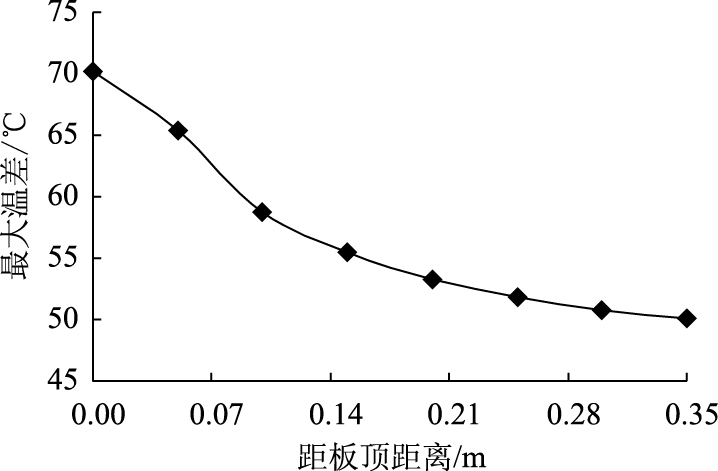
CRC板的厚度取0.35 m,板内不同深度位置的ΔTζ如图 8所示。可见ΔTζ随钢筋埋置深度的增加而减小,这是因为钢筋以上的混凝土层有一定的隔热效果。现行规范[5]建议将钢筋布置在距CRC板顶9 cm和板中位置之间,此时,ΔTζ为54~59 ℃。因此,考虑配筋位置影响时,对于0.35 m板厚,钢筋埋置位置ΔTζ的实际值要比规范法 (ΔTζ=64 ℃) 平均小10%以上,最大达到16%。
|
| 图 8 CRC板不同深度位置的最大温差 Fig. 8 Maximum temperature drop for different depths of CRC slab |
| |
3.3 热传导率对温度参数的影响
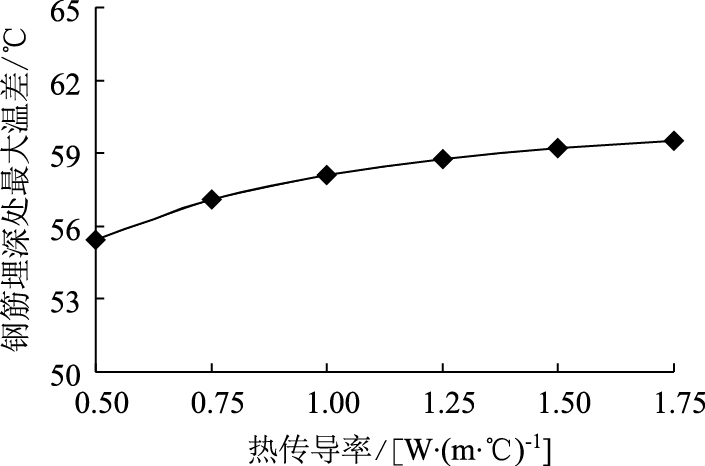
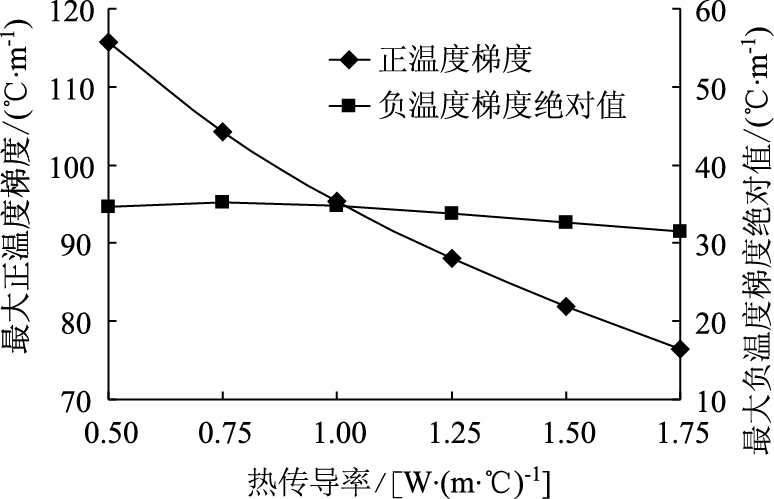
水泥混凝土热传导率K对纵向配筋温度参数的影响见图 9~图 10。K一般取0.5~1.75 W/(m·℃)。
|
| 图 9 混凝土热传导率对最大温差的影响 Fig. 9 Effect of thermal conductivity of concrete on maximum temperature drop |
| |
|
| 图 10 混凝土热传导率对温度梯度的影响 Fig. 10 Effect of thermal conductivity of concrete on temperature gradient |
| |
当K从0.5 W/(m·℃) 增加到1.75 W/(m·℃) 时,钢筋位置的ΔTζ增加了7%,说明混凝土热传导率对ΔTζ有一定影响。负温度梯度的绝对值最大相差3.6 ℃/m,正温度梯度最大相差39.22 ℃/m,说明热传导率对正温度梯度的影响明显。为降低温度翘曲应力,建议使用传热性能较好的水泥混凝土作为CRCP材料。
3.4 比热容对温度参数的影响水泥混凝土比热容C对纵向配筋温度参数的影响见表 5,C一般为800~1 200 J/(kg·℃)。
| 比热容/[J·(kg·℃)-1] | 800 | 900 | 1 000 | 1 100 | 1 200 |
| 最大温差/℃ | 60.53 | 59.98 | 59.42 | 58.92 | 58.44 |
| 最大正温度梯度/(℃·m-1) | 76.74 | 76.64 | 76.40 | 76.05 | 75.61 |
| 最大负温度梯度/(℃·m-1) | -31.39 | -31.36 | -31.25 | -31.09 | -30.86 |
3个参数均随比热容的增加而递减,但是减小的幅度并不明显。因此,CRC板混凝土的比热容对纵向配筋的影响可忽略不计。
4 温度场对结构计算的影响 4.1 潭耒高速公路算例取潭耒高速公路质量提升工程的路面结构和材料参数作为算例[17],分析温度场对配筋设计的影响。基本尺寸同图 2有限元模型。
面层混凝土为C35:抗拉强度ft为3.22 MPa,弹性模量Ec为31.0 GPa,泊松比vc为0.15,线膨胀系数αc为1.1×10-5℃-1,密度ρc为2 400 kg/m3,干缩应变εsh为3.0×10-4。配筋选用HRB335:屈服强度fsy为335 MPa,弹性模量Es为2.0×105MPa,线膨胀系数αs为9.0×10-6 ℃。
钢筋与混凝土之间的剪切刚度系数ks为32 MPa/mm[21]。基层与CRC板间的摩阻力系数kc为50 MPa/m[4, 22]。由于kc是层间黏结-滑移刚度系数和钢筋间距 (150 mm) 的乘积[4, 22],纵向钢筋间距b为124 mm时,kc为41 MPa/m。
按照规范要求[5],对于0.18 m板厚,钢筋只能布置在板中,即埋置深度ζ为0.09 m。由表 1可知,未考虑钢筋的埋置深度时,ΔTζ为64 ℃。结合板厚和深度 (见图 8) 的敏感性分析可知:0.18 m板厚和ζ=0.09 m时,ΔTζ约折减10%,取ΔTζ为58 ℃。由图 9和图 10可知:混凝土热力学性质对ΔTζ的影响较小或不明显。翘曲效应主要考虑负温度梯度引起的表面拉应力影响。由图 5和图 7可知:最大负温度梯度的绝对值Tg为30.55 ℃/m。Kohler指出:纵向配筋主要控制温缩和混凝土干缩引起的结构应力和CRCP表面横向开裂。翘曲应力只占总应力的1%[4]。故分析温度场对配筋设计影响时,重点考虑温缩效应。
4.2 CRCP的结构设计原理文献[4]和[23]在考虑层间摩阻力和钢筋约束的前提下,基于单根带筋板条的受力平衡微分方程,推导了温缩和干缩作用下CRCP的应力与位移。带筋板条长度为2L,钢筋横截面积为As,混凝土横截面积为Ac。得到钢筋最大拉应力σs, max(横向裂缝处)、混凝土最大拉应力σc, max(两条横向裂缝中间) 和混凝土最大位移uc, max(横向裂缝处) 的直角坐标解答如下:
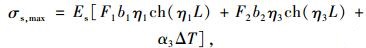
|
(10) |
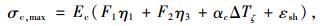
|
(11) |
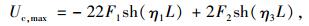
|
(12) |
式中,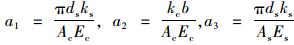
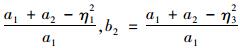
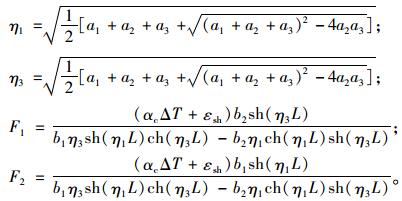
|
(1) 解析法
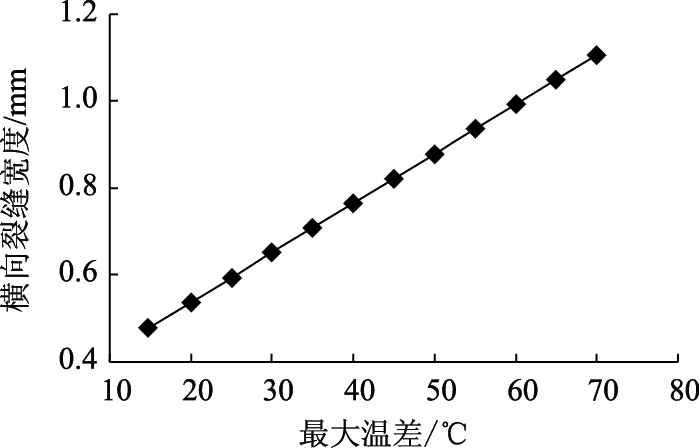
CRCP的纵向配筋指标包括:裂缝宽度bj、裂缝间距s (s=2L) 和钢筋最大拉应力σs, max。在温缩和干缩作用下:σs, max可按式 (10) 计算;bj=2uc, max(由混凝土结构的黏结-滑移理论,横向裂缝两边,板的收缩相同);σc, max用于混凝土板二次开裂的主动控制,与横向裂缝间距有关;s根据钢筋的屈服强度、混凝土的抗拉强度、横向裂缝间距和宽度的上限条件反复推算获得。文章基于潭耒高速公路实体结构,假设L=1.2 m,研究ΔTζ的折减对σs, max,σc, max和bj的影响,见图 11~图 12。
|
| 图 11 最大温差对裂缝宽度的影响 Fig. 11 Effect of maximum temperature drop on cracking width |
| |
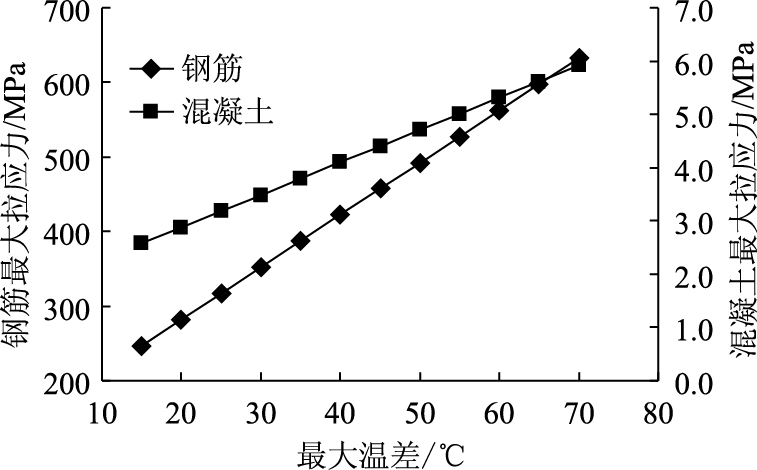
|
| 图 12 最大温差对应力的影响 Fig. 12 Effect of maximum temperature drop on stress |
| |
考虑钢筋埋深的影响时,ΔTζ由64 ℃折减为58 ℃(减幅约10%),bj,σs, max和σc, max分别减小6.6%, 7.1%和6.6%,纵向配筋量随之减小。实际应用中也验证这个问题。按照规范法对潭耒高速公路大修工程进行配筋设计,纵向配筋率需达到0.9%才能满足要求[17]。而路面结构、交通状况和气候条件基本相同的长潭高速公路纵向配筋率为0.6%,从2003年完成改造以来使用效果良好。这说明现行规范对ΔTζ取值时,过于保守。
(2) 规范法
取混凝土的物理参数为:水灰比0.4;用水量为1.4 kN/m;养生系数取1.0。根据规范[5]附表E.0.3-3,摩阻系数 (面层-基层)μ取8.9。由表 1和图 5可知,ΔTζ为64 ℃,Tg为30.55 ℃/m。公路区划Ⅳ区的计算参数k1为0.4,年平均空气相对湿度φa为80%,其他结构参数同前所述。
初拟纵向配筋率为0.90%,设横向裂缝平均间距为1.2 m,求得黏结滑移系数c1为1.567。按照规范[5]公式 (D.0.1-1),横向裂缝平均间距计算值为0.03 m≤1.8 m,满足要求。按规范[5]公式 (D.0.2-1) 和 (D.0.3) 分别计算横向裂缝平均宽度和钢筋最大拉应力,得裂缝平均宽度为0.874 mm,钢筋最大拉应力为439.002 MPa。上述计算是为了比较平均宽度和钢筋最大拉应力的折减规律,计算时并未考虑钢筋屈服强度和裂缝平均宽度最大值的限制。当ΔTζ为58 ℃时,裂缝平均宽度为0.792 mm,钢筋最大拉应力为407.642 MPa,分别减小了约10%和7%。
5 结论文章分析了CRCP温度场的时间和空间分布规律,对CRCP的纵向配筋设计指标进行了修正。主要结论包括:
(1) 温度场和温度梯度均随时间变化,表现出一定周期性。
(2) 温度梯度的极值随CRC板厚度的增加而减小。
(3) 钢筋布置位置的最大温差随着深度的增加而减小。CRC板厚为0.18 m且钢筋布置在板中时,最大温差由64 ℃折减为58 ℃,则横向裂缝宽度、钢筋最大拉应力和混凝土最大拉应力分别减小6.6%, 7.1%和6.6%。按照规范法计算,横向裂缝平均宽度和钢筋最大拉应力减小了约10%和7%。
(4) 增强混凝土的传热性能,可以显著减小CRC板的正温度梯度;而CRC板混凝土的比热容对最大温差和温度梯度的取值影响不大。
文章的成果可以为CRCP的配筋设计和施工质量控制提供参考。施工时,可以选用传热性能较好的混凝土减少温度翘曲应力。考虑钢筋布置位置对最大温差取值的影响时,可以减小设计配筋量,节省造价。由于现有的CRCP改造工程往往在其表面加铺超薄沥青罩面,故后续研究应围绕沥青罩面的隔热作用,对温度参数的取值进行修正。
| [1] | 黄仰贤. 路面分析与设计[M]. 北京: 人民交通出版社, 1998: 457-458. HUANG Yang-xian. Pavement Analysis and Design[M]. Beijing: China Communications Press, 1998: 457-458. |
| [2] | 刘朝晖, 王骁帆, 李盛, 等. 温缩和干缩对连续配筋混凝土路面纵向配筋的影响[J]. 中国公路学报, 2016, 29(11): 1-9 LIU Zhao-hui, WANG Xiao-fan, LI Sheng, et al. Influences of Thermal and Drying Shrinkages on Longitudinal Reinforcement in Continuously Reinforced Concrete Pavement[J]. China Journal of Highway and Transport, 2016, 29(11): 1-9 |
| [3] | WON M, GHEBRAB T, CHOI P, et al. Minimize Premature Distresses in Continuously Reinforced Concrete Pavement[R]. Austin: University of Texas, Austin, 2014. |
| [4] | 左志武. 连续配筋混凝土路面横向裂缝分布和冲断预估研究[D]. 西安: 长安大学, 2010. ZUO Zhi-wu. Study on Distribution of Transverse Cracks and Pounchout Prediction of Continuously Reinforced Concrete Pavement[D]. Xi'an: Chang'an University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010220756.htm |
| [5] | JTG D40—2011, 公路水泥混凝土路面设计规范[S]. JTG D40—2011, Specifications for Design of Highway Cement Concrete Pavement[S]. |
| [6] | 严作人. 层状路面体系的温度场分析[J]. 同济大学学报, 1984, 3(1): 76-85 YAN Zuo-ren. Analysis of the Temperature Field in Layered Pavement System[J]. Journal of Tongji University, 1984, 3(1): 76-85 |
| [7] | 邹晓翎, 谈至明, 钱晨, 等. 路面温度日变化曲线的拟合[J]. 长安大学学报:自然科学版, 2015, 35(3): 40-45 ZOU Xiao-ling, TAN Zhi-ming, QIAN Chen, et al. Curve Fitting of Diurnal Temperature Variations in Pavements[J]. Journal of Chang'an University: Nature Science Edition, 2015, 35(3): 40-45 |
| [8] | 康海贵, 郑元勋, 蔡迎春, 等. 实测沥青路面温度场分布规律的回归分析[J]. 中国公路学报, 2007, 20(6): 13-18 KANG Hai-gui, ZHENG Yuan-xun, CAI Ying-chun, et al. Regression Analysis of Actual Measurement of Temperature Field Distribution Rules of Asphalt Pavement[J]. China Journal of Highway and Transport, 2007, 20(6): 13-18 |
| [9] | WANG D, ROESLER J R, GUO D Z. Analytical Approach to Predicting Temperature Fields in Multilayered Pavement Systems[J]. Journal of Engineering Mechanics, 2009, 135(4): 334-344 |
| [10] | 胡昌斌, 金王杰, 孙增华. 水泥混凝土路面早龄期温度场数值模拟研究[J]. 工程力学, 2013, 30(4): 175-183 HU Chang-bin, JIN Wang-jie, SUN Zeng-hua. Numerical Simulation of Early-age Temperature of Cement Concrete Pavement[J]. Engineering Mechanics, 2013, 30(4): 175-183 |
| [11] | 谈至明, 姚祖康. 非线性温度场下的水泥混凝土路面温度应力计算[J]. 中国公路学报, 1993, 6(4): 9-17 TAN Zhi-ming, YAO Zu-kang. Thermal Stress in Cement Concrete Pavements with Non-liner Temperature Regime[J]. China Journal of Highway and Transport, 1993, 6(4): 9-17 |
| [12] | NISHIZAWA T, SHIMENO S, KOMATSUBARA A, et al. Study on Thermal Stresses in Continuously Reinforced Concrete Pavement[J]. Transportation Research Record, 1998, 1629: 99-107 |
| [13] | 顾兴宇, 倪富健, 董侨. AC+CRCP复合式路面温度场有限元分析[J]. 东南大学学报:自然科学版, 2006, 36(5): 805-809 GU Xing-yu, NI Fu-jian, DONG Qiao. Thermal Analysis for AC+CRCP Composite Pavement Using Finite Element Methods[J]. Journal of Southeast University: Natural Science Edition, 2006, 36(5): 805-809 |
| [14] | 董侨. 沥青混凝土+连续配筋水泥混凝土复合式路面结构与材料研究[D]. 南京: 东南大学, 2006. DONG Qiao. Research on Structure and Material of AC+CRCP Composite Pavement[D]. Nanjing: Southeast University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10286-2007031681.htm |
| [15] | 李盛, 刘朝晖, 李宇峙. CRC+AC复合式路面的合理配筋率[J]. 公路交通科技, 2012, 29(2): 1-6 LI Sheng, LIU Zhao-hui, LI Yu-zhi. Reasonable Reinforcement Ratio of Continuously Reinforced Concrete Composite Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development, 2012, 29(2): 1-6 |
| [16] | 铁摩辛柯, 古迪尔, 徐芝纶, 等. 弹性理论[M]. 北京: 人民教育出版社, 1964. TIMOSHENKO, GOODIER, XU Zhi-lun, et al. Elastic Theory[M]. Beijing: People's Education Press, 1964. |
| [17] | 李盛, 刘朝晖, 李宇峙. 连续配筋混凝土路面纵向配筋方法分析[J]. 公路, 2013(3): 20-25 LI Sheng, LIU Zhao-hui, LI Yu-zhi. Analysis of Longitudinal Reinforcement Method of Continuously Reinforced Concrete Pavement[J]. Highway, 2013(3): 20-25 |
| [18] | 王斌, 黄卫, 杨军, 等. CRCP+AC复合式路面结构损伤与参数敏感性分析[J]. 交通运输工程学报, 2013, 13(5): 17-26 WANG Bin, HUANG Wei, YANG Jun, et al. Analyses of Structural Damage and Parameter Sensitivity for CRCP+AC Composite Pavement[J]. Journal of Traffic and Transportation Engineering, 2013, 13(5): 17-26 |
| [19] | 白桃, 黄晓明, 李昶, 等. 均匀温降下连续配筋混凝土路面 (CRCP) 受力分析[J]. 武汉理工大学学报, 2010, 32(7): 55-59 BAI Tao, HUANG Xiao-ming, LI Chang, et al. Mechanics Analysis of CRCP under Uniform Temperature Drop Condition[J]. Journal of Wuhan University of Technology, 2010, 32(7): 55-59 |
| [20] | 张磊, 黄卫, 王斌, 等. 考虑温度与荷载耦合作用的连续配筋混凝土复合式路面损伤分析[J]. 土木工程学报, 2011, 44(1): 108-114 ZHANG Lei, HUANG Wei, WANG Bin, et al. Analysis of the Damage of CRCP+AC Composite Pavement under Thermal-mechanical Coupling Conditions by FEM[J]. China Civil Engineering Journal, 2011, 44(1): 108-114 |
| [21] | JTG D40—2002, 公路水泥混凝土路面设计规范[S]. JTG D40—2002, Specifications for Design of Highway Cement Concrete Pavement[S]. |
| [22] | 杨慧. 连续配筋混凝土路面结构受力机理研究[D]. 重庆: 重庆交通大学, 2010. YANG Hui. Study on Mechanism of Continuously Reinforced Concrete Pavement CRCP[D].Chongqing: Chongqing Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10618-2010161071.htm |
| [23] | 王衍辉, 张洪亮, 徐士翠. 连续配筋混凝土路面裂缝间距的主动控制[J]. 公路交通科技, 2012, 29(9): 24-29 WANG Yan-hui, ZHANG Hong-liang, XU Shi-cui. Active Crack Spacing Control for Continuously Reinforced Concrete Pavement[J]. Journal of Highway and Transportation Research and Development, 2012, 29(9): 24-29 |
 2017, Vol. 34
2017, Vol. 34
