扩展功能
文章信息
- 何民, 栾庆熊, 税文兵, 于海宁, 樊冬
- HE Min, LUAN Qing-xiong, SHUI Wen-bing, YU Hai-ning, FAN Dong
- 考虑同伴群的行人感知避让社会力改进模型
- An Improved Social Force Model Considering Pedestrian Perception Avoidance Feature of Peer Groups
- 公路交通科技, 2017, 34(3): 125-130
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(3): 125-130
- 10.3969/j.issn.1002-0268.2017.03.017
-
文章历史
- 收稿日期: 2016-06-27
2. 昆明市规划设计研究院, 云南 昆明 650041;
3. 昆明轨道交通集团有限公司, 云南 昆明 650011;
4. 洛阳市规划建筑设计研究院有限公司, 河南 洛阳 471000
2. Kunming Urban Planning & Design Institute, Kunming Yunnan 650041, China;
3. Kunming Rail Transit Group Co., Ltd., Kunming Yunnan 650011, China;
4. Luoyang Urban Planning and Architectural Design and Research Institute, Co., Ltd., Luoyang Henan 471000, China
行人的运动行为是外在环境和内在心理共同作用的结果,具有自主性和随机性等多种特点,行人行为研究是设施布局及制订有效行人活动准则的基础。从安全性和可靠性的角度考虑,基于真人试验研究上述问题的可操作性差。随着仿真技术的快速发展,以计算机语言为载体,以数学模型为输入条件,输出行人行为的方法正逐步成为此类问题研究的主流,而数学模型的建立则是探索一切问题的根本。
社会力模型是一种基于虚拟物理力,时间和空间上均连续的行人行为研究模型,模型雏形由Helbing和Molna[1-2]提出,早期成功地模拟了常态下单、双向行人流的自组织现象,随后引入惶恐因子,模拟了紧急状态下由于行人堵塞而导致的快既是慢、自动跟随等经典现象;模型自提出至今,经历了多次改进:Lakoba[3]等从密度与社会力大小之间的关系、最大允许压缩量与行人重叠之间的关系角度进行分析,提出了最大允许压缩量消除重叠算法对模型进行了改进;Parisi[4]等针对原始模型中存在的行人双方连续冲撞的与现实不符的现象,引入行人私人空间及自停止机制,对模型进行改进;Mehdi Moussaı¨d[5]等对不同时段商业步行街人群出行结构比例进行调查分析,得到了结伴同行出行人群比例远高于个体独立出行比例的结果,以此为基础提出了同伴群的概念,并根据同伴群成员的步行特征,建立了同伴群运动模型;国内学者胡清梅[6]从行人运动的各向异性出发对模型进行了改进,改进模型能够较好地模拟行人对于动态阻塞 (高密度) 区域的避让;汪蕾[7]等从相对速度对社会心理力影响的角度考虑,构建了自我期望速度函数对社会力模型进行了改进;王子甲[8]等将Multi Agent思想与行人微观动力学仿真模型进行融合,引入分子动力学的Gear预测校正法和链接列表元胞算法,基于Agent感知-决策建模方法对模型进行了改进。此外,国内外学者还从其他多个角度考虑,对模型进行了改进,并进行了多次的实证及运用研究[9-14]。
综上所述,经过多次改进的社会力模型已经能够模拟不同环境下行人的步行行为,但依然存在一些不足。上述研究成果多集中于完善特殊环境下行人与环境之间的交互受力以及基于力的模型的搭建,而对行人间细微受力、重复受力以及基于力的模型对行人行为刻画的有效性分析较为欠缺,这不仅加大了模型的复杂度,影响计算机的运算效率,而且难以凸显真实的行人-环境交互行为。以行人实时避让行为为研究对象,分析有效避让的主要影响因素,建立适用于个体及群体的行人避让社会力模型。
1 行人运动数学模型的建立 1.1 模型基本原理加入同伴群作用项的社会力模型由自驱力、行人间作用力及行人与障碍物间的作用力及同伴群作用力构成,模型将行人看作满足运动定律的质点,利用矢量力刻画行人的内在动机及外在受力。何民[15]等考虑到原有模型已经加入了接触力,取消了同伴群模型中的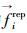
经改进的社会力模型表达式为:
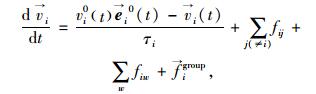
|
(1) |
式中,期望力作用项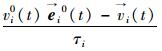
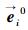
行人间相互作用力fij,反映了行人i与其他行人j间的相互作用,由行人间的社会力和接触力组成,社会力为行人间企图保持一定距离的心理状态的外在描述,接触力因身体碰撞而产生的作用力,由身体挤压力和滑动摩擦力两部分组成,详细表达式如下:
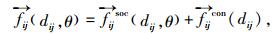
|
(2) |
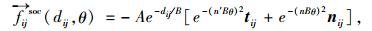
|
(3) |
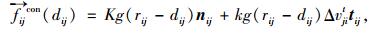
|
(4) |
式中,dij=‖ri-rj‖为行人之间的距离; rij为行人i与行人j的半径和; θ为行人i的坐标向量转向个体j时转过的角度; nij为由行人j指向行人i的单位向量; tij逆时针旋转90°得到nij,tij=Dij/‖Dij‖,Dij=λ(vi-vj)+eij,B=γ‖Dij‖,eij=(xj-xi)/‖xj-xi‖,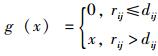
| 参数 | 取值 |
| τ/s | 0.54 |
| λ | 2 |
| n′ | 3 |
| K/(m-1s-1) | 1 200 |
| b/m | 0.3 |
| Δt/s | 0.5 |
| γ | 0.35 |
| β1/s-1 | 4 |
| k/s-2 | 2 400 |
| A/(m·s-2) | 4.5 |
| n | 2 |
| β2/(m·s-2) | 1 |
| a/(m·s-2) | 10 |
人与边界 (或障碍物) 之间的作用力fiw类似行人间的相互作用,由行人与障碍物的社会力和接触力组成,表达式如下所示:
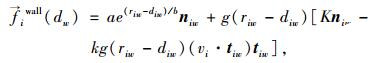
|
(5) |
式中,riw为行人与1/2障碍物厚度之和,即riw=ri+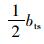
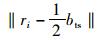
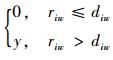
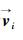
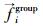
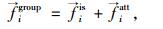
|
(6) |
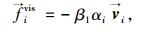
|
(7) |
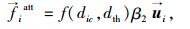
|
(8) |
式中,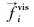
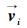
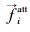
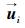
在基于原有模型的双向行人流仿真试验中,低密度状态下,行人与障碍物之间可以顺利地进行交互,但随着人流密度的加大,排斥力不足于维持良好的行人交互,行人之间相互穿透的现象时有发生。为了消除这种现象,引入动态避让作用力算法。
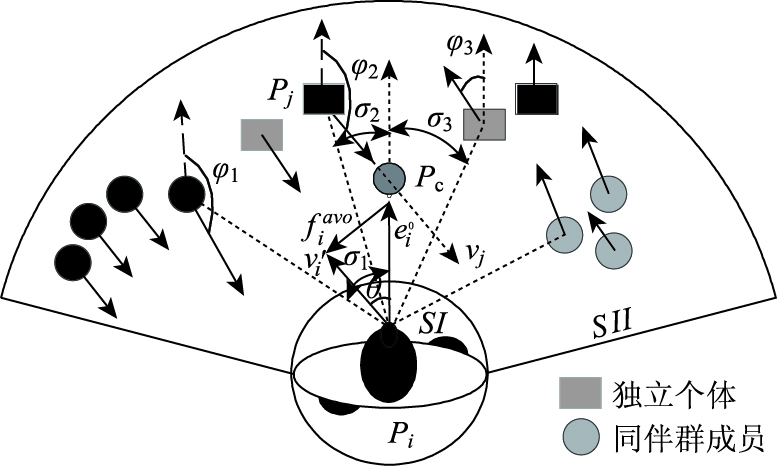
根据真实的行人交互,设定SII为行人i的避让域,SI为行人自身,根据行人的运动习性及模型的演示效果,SII为5ri,扇形角度为150°,如图 1所示,避让规则描述为:
|
| 图 1 避让域及冲突行人的确定 Fig. 1 Determination of avoidance area and conflict pedestrians |
| |
(1) 行人i搜寻行人速度方向与e0i(期望运动方向) 夹角φ大于150°的行人j(φ3 < 150°,不符合);
(2) 计算行人i与行人j质心连线 (虚线连线) 到期望方向e0i的转角σ,如果σ绝对值小于20°(|σ3|>20°,不符合),则确定其为行人i所需避让的人,如图 1所示。
根据上述规则,行人i能够获得一个需要避让的行人集合j[j]。行人i将根据与他人间的位置关系及到达冲突点的时间差,确定避让优先级。双方到达预期冲突点的时间及时间差值ξicj取为如下形式:
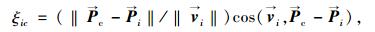
|
(9) |
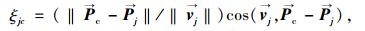
|
(10) |
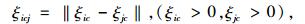
|
(11) |
式中,ξic和ξjc为行人i和行人j运动至预期冲突点的时间;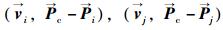
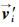
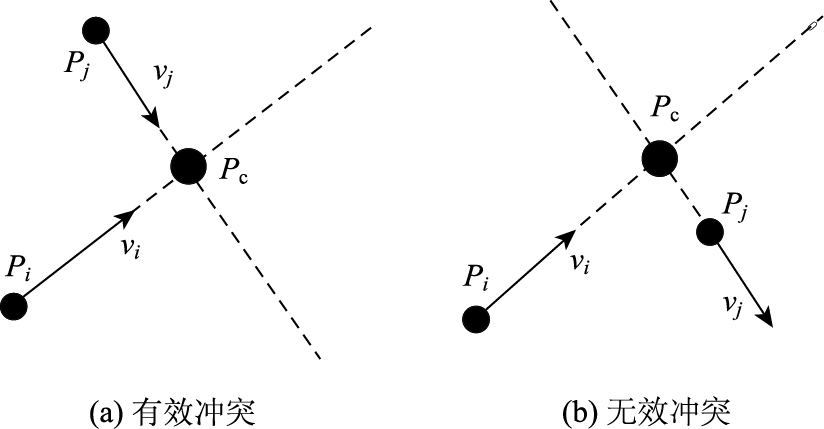
|
| 图 2 行人间冲突形式 Fig. 2 Pedestrian conflict forms |
| |
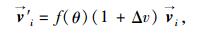
|
(12) |
式中,Δv为随机给定的速度调整量,其取值符合正态分布; f(θ) 为逆时针旋转算子,记为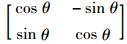
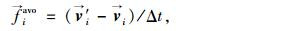
|
(13) |
式中,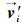
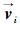
综合上述分析,改进的行人社会力模型表达式为:
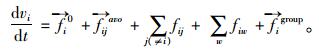
|
(14) |
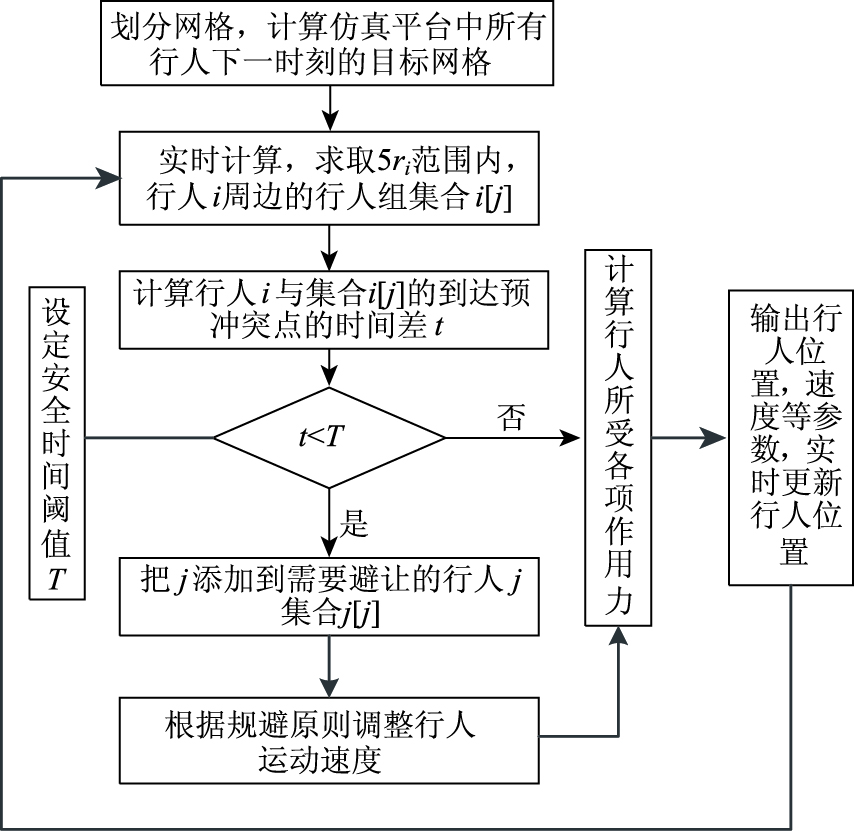
Agent是具备感知、分析、学习等智能行为,可与所处环境及其他实体动态交互、综合决策、调整自我状态的实体。将改进的模型与Agent建模思想融合,确定行人仿真中的冲突检测以及避让的计算流程,以VC++及QT作为开发工具搭建仿真平台。此外,因算法中每一个步长将计算一次距离差,整个算法中存在大量的距离运算,不利于平台的高效运行,利用四叉树空间划分技术,将场景空间划分为离散方格区域,以此提高平台的运行效率。行人冲突检测与避让算法流程如图 3所示。
|
| 图 3 行人冲突检测与避让算法流程 Fig. 3 Flowchart of pedestrian collision detection and avoidance algorithm |
| |
2.2 模型参数标定
根据既有研究[16],结合行人体征的基本情况,设定行人半径r服从[0.25~0.35]的均匀分布、行人期望速度v0i(t) 服从N(1.29,0.19) 的正态分布,相关模型参数标定如表 1所示。
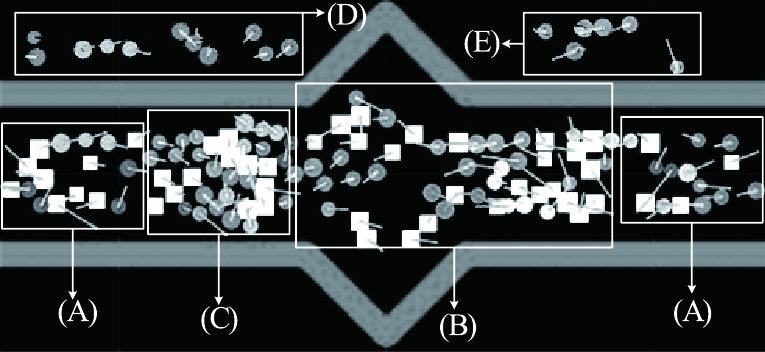
2.3 仿真实现及结果分析为对比改进模型与原有模型,逐次对融入同伴群模型的社会力模型、融入同伴群与避让模型的社会力模型进行模拟。设置的场景参数为:步行道宽5 m,长50 m,上下灰色区域为场景边界,白色方块代表独立个体,不同颜色的实心圆表示同伴群成员,颜色相同的圆表示从属同一个群体的同伴群成员,实物前方实线表示行人的运动速度,同伴群试验中同伴群成员与独立行走个体的比例为7:3[5],设计行人量由25逐步递增至125。仿真截图如图 4~图 6所示。
|
| 图 4 加入同伴群的社会力模型 Fig. 4 Social force model which joined peer group |
| |

|
| 图 5 加入同伴群与避让算法的社会力模型 Fig. 5 Social force model which joined peer group & avoidance algorithm |
| |

|
| 图 6 同伴群避让效果 Fig. 6 Peer group avoidance effect |
| |
基于融入同伴群模型的原有社会力模型仿真效果如图 4所示,低密度区域 (图 4A); 同伴群成员“V”字型、“一”字型、“U”字型等步行结构明显 (图 4D);随着密度的变大 (图 4B),具有一定运动自主性的小同伴群得以产生 (图 4E,同伴群步行结构提取);高密度区域 (图 4C),行人间因期望力的持续作用,碰撞甚至相互穿越的现象出现。而事实上,随着行人双方距离的减小,即将相遇的两个行人会采取减速和错向的方式避让对方。
基于融入动态避让行为的社会力模型仿真效果如图 5所示,从图中可以看出行人具备了一定程度的运动自主性,能够在明确双方位置关系后动态调整自己的运动速度,达到有效避开对方的目的。此外,模型体现了同伴群成员“步调一致、协同避让冲突行人”的实际情况,如图 6所示。
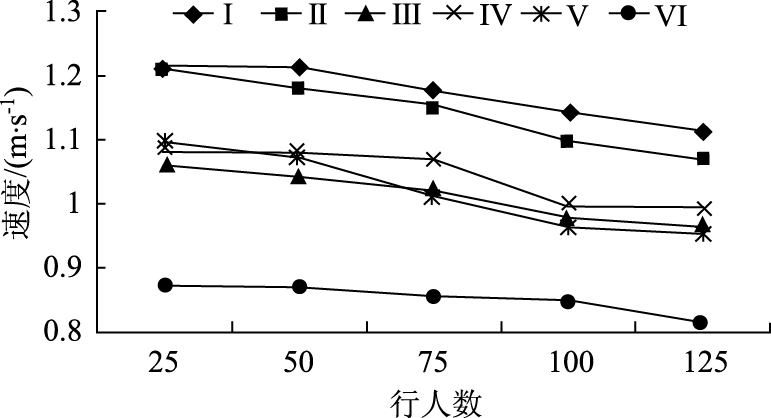
对仿真获取的数据进行分析,仿真结果如表 2所示,拟合后的行人量-速度曲线如图 7所示。
|
| 图 7 行人速度变化曲线图 Fig. 7 Curves of pedestrian speed variation |
| |
| 人数 | 速度值/(m·s-1) | |||||||
| 单向行人流 | 双向行人流 (无避让) | 双向行人流 (有避让) | ||||||
| 个体Ⅰ | 含同伴群Ⅱ | 个体Ⅲ | 含同伴群Ⅳ | 个体Ⅴ | 含同伴群Ⅵ | |||
| 25 | 1.213 | 1.082 | 1.211 | 1.094 | 1.059 | 0.872 | ||
| 50 | 1.211 | 1.078 | 1.177 | 1.072 | 1.042 | 0.868 | ||
| 75 | 1.174 | 1.067 | 1.153 | 1.011 | 1.017 | 0.856 | ||
| 100 | 1.14 | 0.996 | 1.097 | 0.965 | 0.978 | 0.848 | ||
| 125 | 1.113 | 0.993 | 1.068 | 0.953 | 0.965 | 0.814 | ||
如图 7所示,避让行为、同伴群同等控制条件下,随着行人数量的增加,单向行人流速度随行人数量的变化近似于线性变化,而在双向行人流试验中,随着行人数量的递增,对向冲突增多,行人流整体速度呈较快的下降趋势 (Ⅰ与Ⅲ或Ⅱ与Ⅳ对比)。
避让行为、行人流流向同等控制条件下,引入同伴群模型的行人流速度随行人数量的变化呈现较快的下降趋势,双向无避让行人流速度拟合曲线曲率最大,速度下降最快 (Ⅰ与Ⅱ、Ⅲ与Ⅳ或Ⅴ与Ⅵ对比)。
行人流流向、同伴群同等控制条件下,随着行人数量的增加,无避让行为行人流量-速度拟合曲线曲率较大,速度呈较快下降趋势 (Ⅲ与Ⅴ或Ⅳ与Ⅵ对比)。
3 结论避让行为是交通参与者成功摆脱交通冲突的唯一途径。考虑原有社会力模型不能实时、有效解决仿真试验中的行人碰撞及穿越问题,在对行人避让详细分析的基础上,建立融入动态避让行为的行人个体及同伴群社会力改进模型。仿真结果表明:行人个体及同伴群均能有效地避让对其运动产生影响的其他行人,同伴群成员别于个体“结伴同行、协同避让”的步行特征得以体现;单向行人流的通行效率远高于双向行人流;同伴群步行结构极大程度地降低了行人流的整体运动速度,且该现象在双向行人流中表现得更加明显;避让行为的引入成功解决了行人间靠碰撞改变合力方向进行避让的步行模式,减缓了行人碰撞前后的速度变化。
| [1] | HELBING D, MOLNÁR P. Social Force Model for Medestrian Dynamics[J]. Physical Review E:Statistical Physics Plasmas Fluids Related Interdisciplinary Topics, 1995, 51(5): 4282-4286 |
| [2] | HELBING D, FARKAS I, VICSEK T. Simulating Dynamical Features of Escape Panic[J]. Nature, 2000, 407(6803): 487-90 |
| [3] | LAKOBA T I, KAUP D J, FINKELSTEIN N M. Modifications of the Helbing-Molnár-Farkas-Vicsek Social Force Model for Pedestrian Evolution[J]. Simulation Transactions of the Society for Modeling & Simulation International, 2005, 81(5): 339-352 |
| [4] | PARISI D R, GILMAN M, MOLDOVAN H. A Modification of the Social Force Model Can Reproduce Experimental Data of Pedestrian Flows in Normal Conditions[J]. Physica A:Statistical Mechanics & Its Applications, 2009, 388(17): 3600-3608 |
| [5] | MOUSSAÏD M, PEROZO N, GARNIER S, et al. The Walking Behaviour of Pedestrian Social Groups and Its Impact on Crowd Dynamics[J]. Plos One, 2010, 5(4): e10047 |
| [6] | 胡清梅, 方卫宁, 邓野. 一种基于社会力的行人运动模型研究[J]. 系统仿真学报, 2009, 21(4): 977-980 HU Qing-mei, FANG Wei-ning, DENG Ye. Research on Pedestrian Movement'S Model Based on Social Force[J]. Journal of System Simulation, 2009, 21(4): 977-980 |
| [7] | 汪蕾, 蔡云, 徐青. 社会力模型的改进研究[J]. 南京理工大学学报:自然科学版, 2011, 35(1): 144-149 WANG Lei, CAI Yun, XU Qing. Modifications to Social Force Model[J]. Journal of Nanjing University of Science and Technology:Natural Science Edition, 2011, 35(1): 144-149 |
| [8] | 王子甲, 陈峰, 施仲衡. 基于Agent的社会力模型实现及地铁通道行人仿真[J]. 华南理工大学学报:自然科学版, 2013, 41(4): 90-95 WANG Zi-jia, CHEN Feng, SHI Zhong-heng. Agent-Based Realization of Social Force Model and Simulation of Pedestrians in Subway Passageway[J]. Journal of South China University of Technology:Natural Science Edition, 2013, 41(4): 90-95 |
| [9] | ZANLUNGO F, IKEDA T, KANDA T. Social Force Model with Explicit Collision Prediction[J]. Epl, 2011, 93(6): 3437-3442 |
| [10] | YANG X, DAAMEN W, HOOGENDOORN S P, et al. Breakdown Phenomenon Study in the Bidirectional Pedestrian Flow[J]. Transportation Research Procedia, 2014, 2: 456-461 |
| [11] | 黄鹏, 刘箴. 一种面向人群仿真的改进型社会力模型研究[J]. 系统仿真学报, 2012, 24(9): 1916-1919 HUANG Peng, LIU Zhen. Study on Improved Social Force Model for Crowd Simulation[J]. Journal of System Simulation, 2012, 24(9): 1916-1919 |
| [12] | 张海均, 施化吉. 改进社会力的双向行人流模型研究[J]. 计算机工程与应用, 2013, 49(16): 236-239 ZHANG Hai-jun, SHI Hua-ji. Research of Bi-directional Pedestrian Flow's Model on Modification of Social Force[J]. Computer Engineering and Applications, 2013, 49(16): 236-239 |
| [13] | 王爱丽, 董宝田, 王泽胜. 基于社会力的行人交通微观仿真模型研究[J]. 系统仿真学报, 2014, 26(3): 662-669 WANG Ai-li, DONG Bao-tian, WANG Ze-sheng. Modeling and Simulation of Microscopic Pedestrian Based on Social Force[J]. Journal of System Simulation, 2014, 26(3): 662-669 |
| [14] | 隋杰, 万佳慧, 于华. 基于社会力的应急疏散仿真模型应用研究[J]. 系统仿真学报, 2014, 26(6): 1197-1201 SUI Jie, WAN Jia-hui, YU Hua. Research on Simulation of Emergency Evacuation Based on Social Force Model[J]. Journal of System Simulation, 2014, 26(6): 1197-1201 |
| [15] | 何民, 樊冬, 栾庆熊, 等. 行人同伴群社会力学仿真[J]. 北京工业大学学报, 2015, 41(3): 419-425 HE Min, FAN Dong, LUAN Qing-xiong, et al. Social Dynamics Simulation of Pedestrian Social Groups[J]. Journal of Beijing Institute of Technology, 2015, 41(3): 419-425 |
| [16] | MOUSSAÏD M, HELBING D, GARNIER S. Experimental Study of the Behavioural Mechanisms Underlying Self-organization in Human Crowds[J]. Proceedings of the Royal Society Biological Sciences, 2009, 276(1668): 2755-2762 |
 2017, Vol. 34
2017, Vol. 34
