扩展功能
文章信息
- 赵靖, 马万经, 廖大彬
- ZHAO Jing, MA Wan-jing, LIAO Da-bin
- 基于宏观基本图的交通小区通过量最大化控制方法
- A Method for Controlling Maximum Throughput in Traffic Subarea Based on Macroscopic Fundamental Diagram
- 公路交通科技, 2017, 34(3): 110-116
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(3): 110-116
- 10.3969/j.issn.1002-0268.2017.03.015
-
文章历史
- 收稿日期: 2016-05-30
2. 同济大学 交通运输工程学院, 上海 201804;
3. 武汉市规划设计有限公司, 湖北 武汉 430014
2. School of Transportation Engineering, Tongji University, Shanghai 201804, China;
3. Wuhan Planning and Design Co., Ltd., Wuhan Hubei 430014, China
交通拥堵是各城市为之困扰的问题,它造成交通环境恶化和出行成本加剧。为了提升重点区域信号控制的协调性和运行效率,在单点及干线信号控制系统研究的基础上,区域交通信号控制系统孕育而生。其控制方法在早期仅将相位差作为优化参数[1],后经研究人员不断优化,现已实现了区域动态交通控制,将相位差、绿灯时间及周期均进行优化[2-3]。在此基础上,开发形成了TRANSYT,SCOOT,SCATS等多种区域控制系统。
但在实践中发现,区域交通运行水平与区域内道路交通量关系密切,若饱和度高或过饱和,区域交通控制难以达到预期效果。因此,交通小区的控制不仅包括内部交叉口的信号控制,还包括交通小区的驶入和驶出交通量的控制。Daganzo等[4-5]研究发现,流出网络车辆数和网络内车辆数之间存在抛物线的关系,即在某网络内车辆数达到某数值时,流出网络的车辆数存在一个最大值,网络整体运行效率达到最高。
自宏观基本图被揭示之后,围绕其存在性的研究首先展开。姬杨蓓蓓[6]、He[7]、卢守峰[8]、王福建[9]等利用仿真、道路检测器数据或出租车的数据,分别对荷兰阿姆斯特丹、北京三环、长沙中心城区的路网进行了研究,均验证了宏观基本图的存在性, 但其具体形态受交通条件、道路条件、管控条件等因素影响。其中,对交通条件的研究源于Geroliminis[10]在对实际数据分析中发现的滞回现象,即所采集的数据在流量与占有率比例关系图形中构成封闭曲线,而不是线性曲线。引起这种现象的主要原因在于网络中密度分布的不均匀以及所采集的数据量不足。此后,研究发现交通不均匀分布[11-12]、外部需求剧烈变化[13-14]、交通转向比例[15]、不同交通方式比例及空间分布[16-17]等均会对宏观基本图及其滞回现象产生影响。
对于影响宏观基本图的因素,研究人员发现不同路网结构具有不同宏观基本图,路网结构的均匀性、路网中干线是否双向通行等因素对宏观基本图具有较大影响[18-19]。此外,道路禁行[13]、路径选择方式[14]、信号控制[20]、检测器位置[21]、诱导信息[22]等也会对宏观基本图产生影响。
随着对宏观基本图基本性质及影响因素的深入研究,研究人员开始将其运用于网络控制。
在宏观基本图被提出之初,Geroliminis[5]就指出可通过控制交通需求来提高道路可达性。王福建依据该理念,采用密度及速度作为交通状态判别拥堵评价指标,将网络交通流的运行情况及拥堵程度划分为5个等级,并总结了对趋于拥堵的路网实施控制的策略思想,提出了基于宏观基本图的城市管理的一些措施[23]。此后,Mehdi[24]研究了采用反馈控制对网络交通进行控制的可行性及实施条件。Yoshiit[25]特别针对城市快速路网,将宏观基本图运用到过饱和网络控制中,提出了一种区域计量控制方法,并通过对阪神快速路网的仿真研究验证了该方法的有效性。
综上所述,目前研究已证实网络宏观基本图的存在,且关于其影响因素的研究也日趋成熟。但具体的控制方法主要集中于城市快速路网,缺少针对地面道路交通小区的控制方法以及定量化的控制效果分析。
本研究将基于宏观基本图理论,针对地面道路交通小区,建立以通过量最大为目标的反馈控制方法, 通过实时检测控制小区内部车辆数及进入小区的车辆数,确保小区始终处于最佳的运行状态, 并通过Vissim仿真对控制效果进行定量化验证。
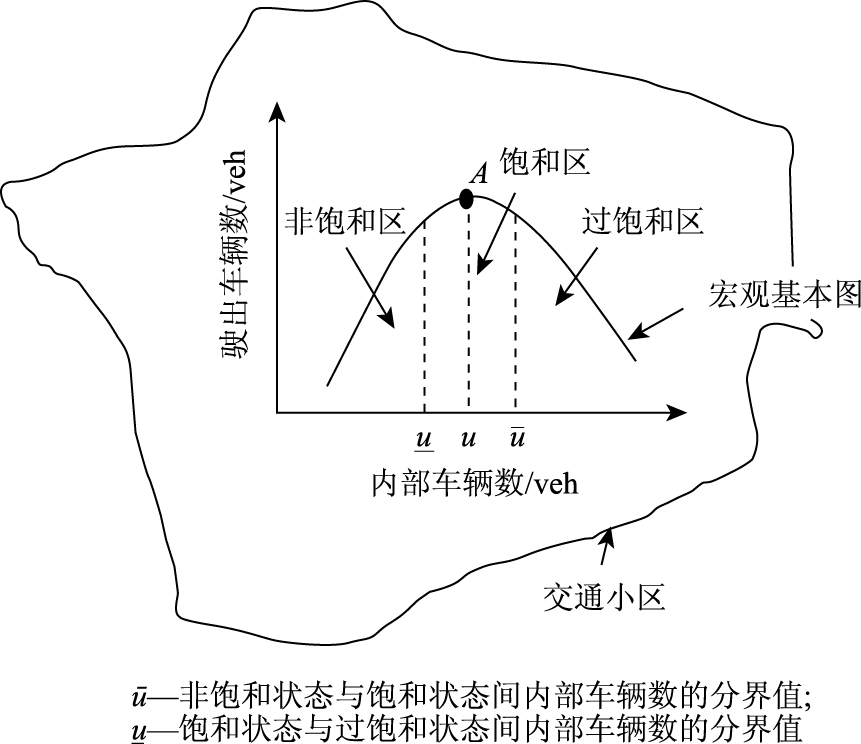
1 控制思想提出小区宏观基本图如图 1所示。为使整个小区交通保持稳定最优运行状态,需根据小区内部交通状态,实时控制小区外部驶入交通,以确保小区内部交通量在最佳车辆数u附近波动,使得小区驶出车辆数达到最大,从而确保小区运营的稳定及效益最优。
|
| 图 1 试验小区宏观基本图 Fig. 1 Macroscopic fundamental diagram of test subarea |
| |
由图 1可见,小区宏观基本图可分为3个阶段。第1阶段,在小区内部交通量较小时,整个小区驶出交通量随着小区内部交通量的增大而增大;第2阶段,当小区内部交通量在最佳车辆数附近波动时,整个小区驶出交通量达到最大,并在该最大值附近波动;第3阶段,当小区内部交通量超过最佳车辆数时,整个小区驶出交通量随着小区内部交通量的增大而减小。
因此,控制的关键在于维持小区内部车辆数在最佳车辆数附近,通过控制外部驶入交通量,防止进入第3阶段,使小区驶出交通量最大。
2 控制方法设计 2.1 控制目标针对宏观基本图已知的交通小区,本研究控制目标是使得交通小区通过量最大化,如式 (1) 所示:
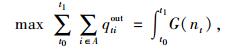
|
(1) |
式中,qtiout为控制周期t边界交叉口i实际驶出的交通量;G(nt) 为小区内部车辆数等于nt情况下的小区驶出车辆数;t0和t1分别为分析开始和结束时刻;A为边界交叉口集合。
上述优化目标可通过反馈控制实现。通过检测器实时检测小区驶入驶出车辆数,得到各个时刻交通小区内部车辆数,进而通过控制外部驶入交通量,确保交通小区内部车辆数不大于最佳车辆数,使交通小区始终处于最佳运行状态。每个控制周期t允许驶入小区的总车辆数为:
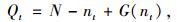
|
(2) |
式中,Qt为控制周期t允许驶入小区的总车辆数;N为小区内部最佳车辆数,可由小区宏观基本图获得。
其中控制周期t小区内部车辆数nt可通过小区前一控制周期内的车辆数及驶入驶出交通量计算得到,即:
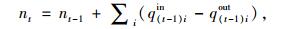
|
(3) |
式中qtiin为控制周期t边界交叉口i实际驶入交通量。
由此,若已知控制初始状态小区内部车辆数和各控制周期驶入驶出小区的交通量,便可计算各控制周期允许驶入小区的总车辆数。实际应用中可选取凌晨小区内车辆数几乎为0的时段作为控制初始状态。
2.2 驶入交通量分配上节确定了每个控制周期t允许驶入小区的总车辆数,下面根据各边界上游控制点的交通需求和通行能力,将允许驶入小区的总车辆数在各控制点进行分配。具体分配流程分为以下5个步骤。
步骤1(初始化):确定边界上游信号交叉口进口道通行能力、最大绿灯时间下的通行能力、外部交通需求和总驶入流量。
步骤2(初次分配):按等饱和度原则,对允许驶入交通量在各边界进口进行分配。
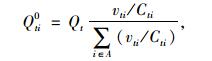
|
(4) |
式中,Qti0为控制周期t初次分配中边界进口i允许驶入小区的车辆数;vti为控制周期t边界进口i的实际交通需求;Cti为控制周期t边界进口i的最大可通行车辆数,可通过最长绿灯时间和饱和流率计算。
步骤3(通行能力约束):判断各边界进口所分配的允许驶入交通量是否存在超过边界进口按最长绿灯时间计算的通行能力,若是,进入步骤4;若否,进入步骤5。
步骤4(允许驶入交通量调整):对于所分配的允许驶入交通量超过通行能力的边界进口,应按通行能力对允许驶入交通量进行调整,其余进口按等饱和度原则重新进行分配,如式 (5) 所示。j+1,返回步骤3。
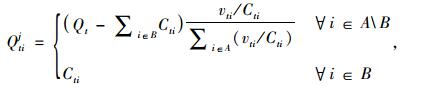
|
(5) |
式中,Qtij为控制周期t的第j次分配中边界进口i允许驶入小区的车辆数;B为所有允许驶入交通量达到通行能力的边界进口的集合。
步骤5(驶入交通量确定):考虑实际交通需求量,各边界进口i控制周期t预期驶入车辆数可按式 (6) 确定,结束。
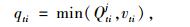
|
(6) |
式中qti为控制周期t边界进口i在信号控制中预期驶入小区的车辆数。
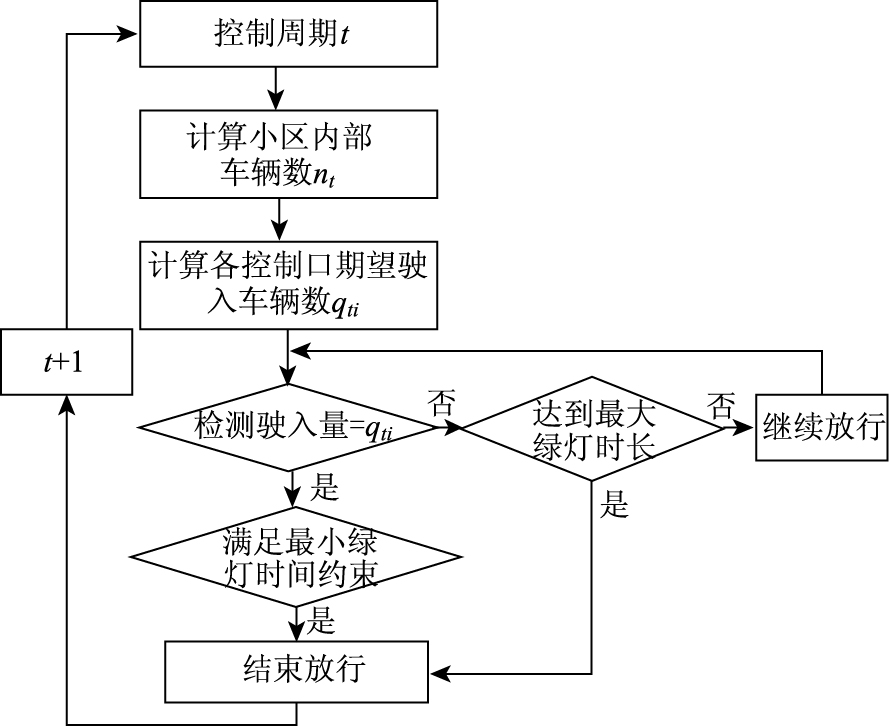
2.3 信号控制方案制订采用感应控制对边界进口交通量进行控制,控制流程如图 2所示, 其中考虑了最小和最大绿灯时长要求。由于在最小绿灯时长不满足情况下进口流量势必很小,因此适当延长绿灯时长不会对交通小区内车辆数的增加造成很大影响。
|
| 图 2 感应信号控制流程 Fig. 2 Flowchart of actuated signal control |
| |
3 控制效果检验 3.1 仿真场景构建
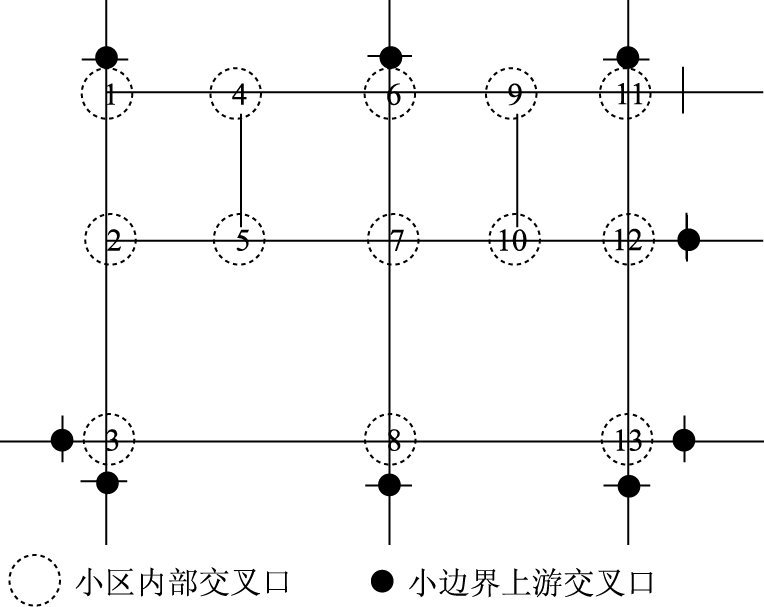
通过仿真,对比分析采用上述控制方法前后小区的运行状态。仿真路网如图 3所示,共有10条进出道路,均为双向4车道。仿真小区中所有内部机动车都通过边界交叉口进出。交通小区内部交叉口均采用两相位定时信号控制,周期时长为120 s,左直右转向比例为1:2:1,边界上游交叉口采用周期为120 s的感应控制。因此,小区的控制周期和数据采集周期均为120 s。仿真中仅考虑小客车。初始状态仿真路网中车辆数为0。边界上游所有进口交通需求变化情况为:初期200 pcu/h,然后每0.5 h增加200 pcu/h,直到第6 h,进口交通需求为2 400 pcu/h,此后需求保持不变,仿真共持续9 h。边界上游交叉口感应信号控制通过VAP模块实现。
|
| 图 3 试验小区路网 Fig. 3 Test road network |
| |
对边界上游交叉口有/无控制两种情况下的小区运行状况进行仿真对比。为消除仿真随机性影响,在同一情况下仿真5次,并对最后结果取均值。
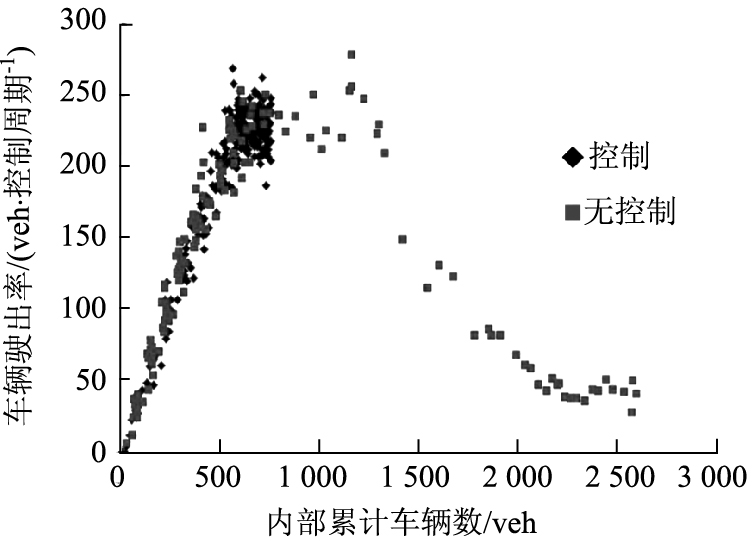
3.2 交通小区宏观基本图分析首先运行无边界控制的情况,发现小区存在宏观基本图,如图 4所示。随着小区内部累计车辆数的逐渐增加,整个小区的驶出车辆数逐步增大;当驶出车辆数达到240 veh/控制周期左右,内部累计车辆数达到800 veh左右时,整个小区的驶出车辆数不再随小区内部累计车辆数的增大而增加,小区驶出车辆数维持在一个相对稳定的状态;随着整个小区内部累计车辆数进一步增大,整个小区驶出车辆数逐步减小,当内部累计车辆数达到2 500 veh左右时,小区驶出车辆数趋近最小值。小区最佳内部车辆数约为800 veh,最大驶出流量约为240 veh/控制周期。
|
| 图 4 试验小区宏观基本图 Fig. 4 Macroscopic fundamental diagram of test subarea |
| |
在获取交通小区宏观基本图特征的情况下,对其进行驶入交通量控制,运行结果如图 4所示。随着小区内部车辆数的逐步增加,小区每控制周期内驶出车辆数逐步增大,当小区内部车辆数达到800辆左右时,小区每控制周期内驶出车辆数趋于稳定状态,约为230 veh左右。随着仿真时间的增加,整个小区每控制周期内驶出车辆数在200~250 veh之间波动。可见本文所提出的控制策略可使交通小区运行集中在小区宏观基本图的左边部分,使其始终保持良好的运行状态,车辆驶出率提高近4倍。
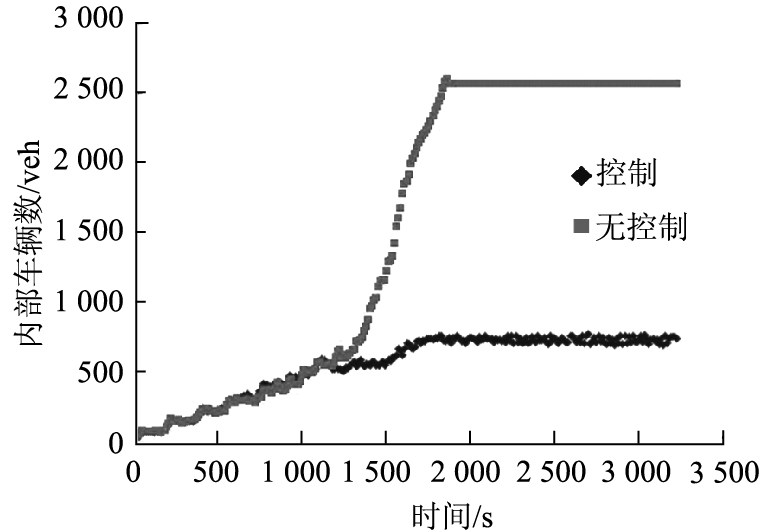
进一步对有/无边界控制条件下小区内部车辆数随时间变化情况进行分析,如图 5所示。在无边界控制情况下,小区内部车辆数会不断累积,最终稳定在2 500 veh左右,远远超过了800 veh小客车的最佳内部车辆数,使得在仿真中后期,路网始终处于低效的通行状态。而在有边界控制情况下,随着仿真时间的逐步增大,内部车辆数逐步增大,最后稳定在800 veh小客车左右,使得路网保持稳定高效运行状态。
|
| 图 5 仿真时段内试验小区内部车辆数的变化 Fig. 5 Number of vehicles in test subarea during simulation |
| |
3.3 交通小区服务水平分析
有/无边界控制情况下的仿真试验小区总体运行情况如表 1所示。采用边界控制交通小区的运行水平显著高于无边界控制的情况。其中,边界控制使分析时段总延误降低49%,驶出车辆数增加147%,总行程时间减少35%。
| 运营指标 | 有控制 | 无控制 | 优化比例/% |
| 总延误/h | 13 756.88 | 26 966.91 | 49 |
| 驶出车辆/veh | 50 211 | 20 318 | 147 |
| 总行程时间/h | 18 985.52 | 29 167.07 | 35 |
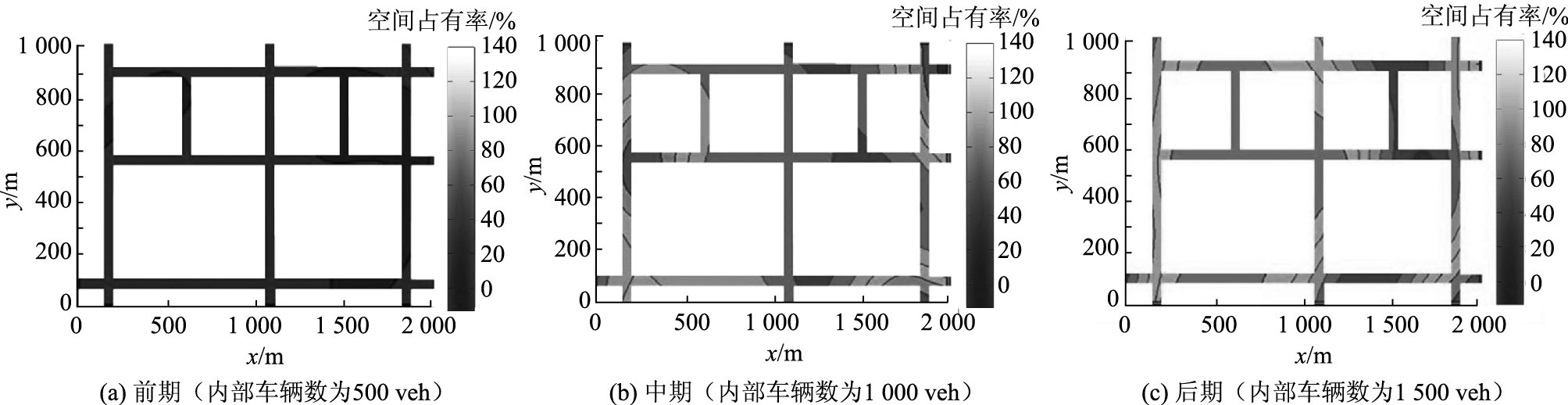
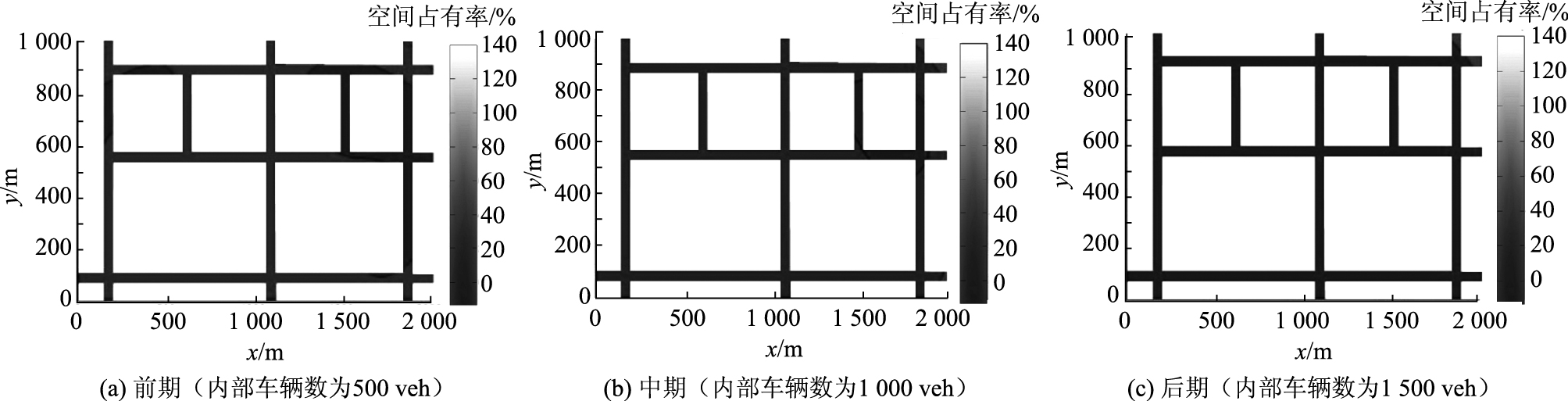
具体分析小区在有/无边界控制情况下内部交通的演变情况,选取仿真前期、中期及仿真后期3个时间段小区内部路段空间占有率变化情况进行对比,分别如图 6、图 7所示。其中横纵坐标表示小区路段的位置坐标,不同灰度代表不同路段空间占有率水平。
|
| 图 6 无控制情况下仿真小区道路占有率分布图 Fig. 6 Distribution road occupancies at simulation subarea without control |
| |
|
| 图 7 有控制情况下仿真小区道路占有率分布图 Fig. 7 Distribution road occupancies at simulation subarea with control |
| |
可以看出,在仿真开始阶段,有/无控制时小区道路空间占有率情况基本一致,无明显差异。当仿真运行到中期时,由图 6(b)可见,在无控制情况下,小区部分道路开始出现高占有率情况,说明局部交叉口已发生拥堵并有溢流现象。到仿真后期时,由图 6(c)可见,在无控制情况下,小区运行已演化为大面积的交叉口及路段拥堵,导致整个小区交通处于瘫痪状态。而整个运行过程中有边界控制情况下,路段的占有率均较小,说明控制策略可使小区的驶入驶出车辆数达到动态平衡,整个小区处于最佳运行状态,直到仿真结束。
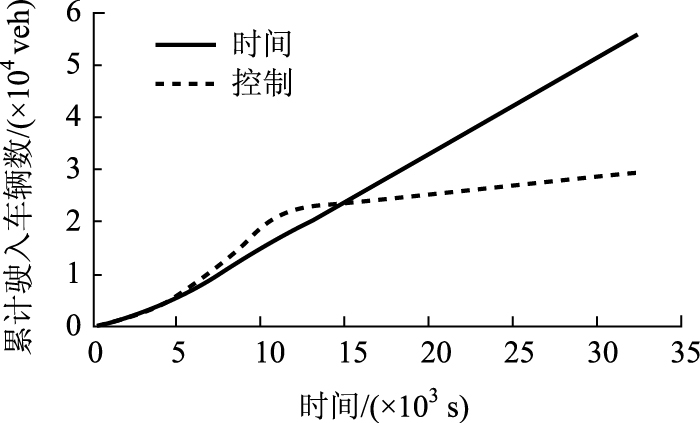
边界控制可提高小区内部的交通运行效率,但以往对其主要的反对意见是质疑边界控制限制了外围车辆的进入,从而在交通小区入口处产生超长排队。针对这一质疑,进一步分析了仿真时段内累计驶入车辆数随时间的变化情况,如图 8所示。
|
| 图 8 累计驶入车辆数 Fig. 8 Accumulative number of vehicles |
| |
可见,只是在边界控制的初期 (8 000~14 000 s),有控制情况下的累计驶入车辆数小于无控制的情况。而随着仿真时间的推移,边界控制的优势开始显现,其累计驶入车辆数显著大于无控制的情况。此时有控制情况下的外围车辆的排队数必然显著小于无控制的情况。这是由于在控制初期,控制方案就将小区内的车辆数控制在最佳运行状态附近,限制了部分车辆的进入。此时由于小区路网尚未饱和,因此无控制情况下车辆仍能持续进入。但当小区路网进入拥挤状态、运行效率急剧降低、无控制的条件下,驶入驶出小区的交通量均很小。此时边界控制虽然表面上人为限制了车辆的驶入,但实质反而有助于车辆的驶入驶出。
该分析表明,若交通小区高峰时段较长,边界控制有助于提高外围车辆驶入小区的效率,并减少入口处的排队长度。
4 结论(1) 从控制小区通行效率角度分析,在拥挤状况下对外部需求进行控制是十分必要的,可使小区运行集中在小区宏观基本图的左半部分,否则将出现仿真试验中的道路大面积瘫痪状态。
(2) 无论小区有无边界控制,随着交通需求的增加,路网总能达到一个相对稳定状态,所不同的是,采用了驶入交通量控制后,路网处于高效运行的稳定状态,在拥挤状态下可提高车辆驶出率近4倍。
(2) 所设计的交通小区边界控制方法可显著提升控制小区的服务水平。试验中可使总延误降低49%,驶出车辆数增加147%,总行程时间减少35%。
(4) 若交通小区高峰时段较长,边界控制有助于提高外围车辆驶入小区的效率,并减少小区边界处的排队长度。
本研究仅针对单个交通小区,但对于路网整体运行效益,单个小区的最优控制可能造成拥堵转移。后续应建立考虑控制子区间驶入驶出交通量的协调控制模型,确保相邻小区整体处于最优的运行状态。此外,在实践中,描述控制小区的宏观基本图是实施本控制方案的前期工作,应充分考虑小区边界不受控进出道路的交通量,将其在允许驶入交通量中剔除。后续研究可选择典型路网,进一步评估优化方法的应用效果。
| [1] | GARTNER N H, LITTLE J D C, GABBAY H. Optimization of Traffic Signal Settings by Mixed Integer Linear Programming Part I:the Network Coordination Problem[J]. Transportation Science, 1975, 9(4): 321-343 |
| [2] | 龙建成, 高自友, 任华玲. 城市网络交通动态信号控制方法[J]. 中国公路学报, 2009, 22(4): 108-114 LONG Jian-cheng, GAO Zi-you, REN Hua-ling. Dynamic Signal Control Method of Urban Network Traffic[J]. China Journal of Highway and Transport, 2009, 22(4): 108-114 |
| [3] | 韩印, 邢冰, 姚佼, 等. 混合交通流条件下区域交通信号控制优化模型[J]. 交通运输工程学报, 2015, 15(1): 119-126 HAN Yin, XING Bing, YAO Jiao, et al. Optimal Model of Regional Traffic Signal Control under Mixed Traffic Flow Condition[J]. Journal of Traffic and Transportation Engineering, 2015, 15(1): 119-126 |
| [4] | DAGANZO C F. Urban Gridlock:Macroscopic Modeling and Mitigation Approaches[J]. Transportation Research Part B:Methodological, 2007, 41(1): 49-62 |
| [5] | GEROLIMINIS N, DAGANZO C F. Existence of Urban-Scale Macroscopic Fundamental Diagrams:Some Experimental Findings[J]. Transportation Research Part B:Methodological, 2008, 42(9): 759-770 |
| [6] | 姬杨蓓蓓, DAAMEW. 阿姆斯特丹城市道路线圈检测器布设方法研究[J]. 重庆交通大学学报:自然科学版, 2010, 29(5): 754-757 JIYANG Bei-bei, DAAME W. Loop Detector Location Research on Urban Road in Amsterdam[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2010, 29(5): 754-757 |
| [7] | HE Z, HE S, GUAN W. A Figure-eight Hysteresis Pattern in Macroscopic Fundamental Diagrams and Its Microscopic Causes[J]. Transportation Letters, 2015, 7(3): 133-142 |
| [8] | 卢守峰, 王杰, 刘改红, 等. 基于流量和出租车GPS数据的城市道路网络宏观基本图[J]. 公路交通科技, 2014, 31(9): 138-144 LU Shou-feng, WANG Jie, LIU Gai-hong, et al. Macroscopic Fundamental Diagram of Urban Road Network Based on Traffic Volume and Taxi GPS Data[J]. Journal of Highway and Transportation Research and Development, 2014, 31(9): 138-144 |
| [9] | 王福建, 孙凌涛, 钱伟. 基于改进后冲击波剖面模型的宏观基本图特性研究[J]. 公路交通科技, 2016, 33(4): 127-133 WANG Fu-jian, SUN Ling-tao, QIAN Wei. Characteristics of Macroscopic Fundamental Diagram Based on SPM[J]. Journal of Highway and Transportation Research and Development, 2016, 33(4): 127-133 |
| [10] | GEROLIMINIS N, SUN J. Hysteresis Phenomena of a Macroscopic Fundamental Diagram in Freeway Networks[J]. Transportation Research Part A:Policy and Practice, 2011, 45(4): 966-979 |
| [11] | SHI X, LIN H. Exploring the Characteristics of Hysteresis Phenomena of Macroscopic Fundamental Diagram for Urban Expressway Network:The Case of Shanghai[C]//Transportation Research Board 93rd Annual Meeting. Washington, D.C.:Transportation Research Board, 2014. |
| [12] | JIN P J, ZHANG J, RAN B. An Automatic Calculation Method of Identifying the Hysteresis Loop Characteristics in Macroscopic Fundamental Diagram[C]//Transportation Research Board 93rd Annual Meeting. Washington, D.C.:Transportation Research Board, 2014. |
| [13] | 许菲菲, 何兆成, 沙志仁. 交通管理措施对路网宏观基本图的影响分析[J]. 交通运输系统工程与信息, 2013, 13(2): 185-190 XU Fei-fei, HE Zhao-cheng, SHA Zhi-ren. Impacts of Traffic Management Measures on Urban Network Microscopic Fundamental Diagram[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(2): 185-190 |
| [14] | 朱琳, 于雷, 宋国华. 基于MFD的路网宏观交通状态及影响因素研究[J]. 华南理工大学学报:自然科学版, 2012, 40(11): 138-146 ZHU Lin, YU Lei, SONG Guo-hua. MFD-based Investigation into Macroscopic Traffic Status of Urban Networks and Its Influencing Factors[J]. Journal of South China University of Technology:Natural Science Edition, 2012, 40(11): 138-146 |
| [15] | GEROLIMINIS N, BOYAC B. The Effect of Variability of Urban Systems Characteristics in the Network Capacity[J]. Transportation Research Part B:Methodological, 2012, 46(10): 1607-1623 |
| [16] | GEROLIMINIS N, DANES J, ESTRADA M. Multimodal Macroscopic Fundamental Diagram for "Car-Bus" Mixed Traffic Signalized Corridors:Application in City of Barcelona, Spain[C]//Transportation Research Board 92nd Annual Meeting. Washington, D. C.:Transportation Research Board, 2013. |
| [17] | ZHENG N, GEROLIMINIS N. On the Distribution of Urban Road Space for Multimodal Congested Networks[J]. Procedia-Social and Behavioral Sciences, 2013, 80: 119-138 |
| [18] | BUISSON C, LADIER C. Exploring the Impact of Homogeneity of Traffic Measurements on the Existence of Macroscopic Fundamental Diagrams[J]. Transportation Research Record, 2009, 2124: 127-136 |
| [19] | KNOOP V L, DE JONG D, HOOGENDOORN S. The Influence of the Road Layout on the Network Fundamental Diagram[J]. Transportation Research Record, 2014, 2421: 22-30 |
| [20] | ZHANG L, GARONI T M, GIER J D. A Comparative Study of Macroscopic Fundamental Diagrams of Arterial Road Networks Governed by Adaptive Traffic Signal Systems[J]. Transportation Research Part B:Methodological, 2013, 49(2): 1-23 |
| [21] | COURBON T, LECLERCQ L. Cross-comparison of Macroscopic Fundamental Diagram Estimation Methods[J]. Procedia-Social and Behavioral Sciences, 2011, 20(6): 417-426 |
| [22] | ZHAO T T, LI Z H, MU B P, et al. Exploring the Influence of Real-time Traveler Information on the Macroscopic Fundamental Diagrams[C]//11th International Conference of Chinese Transportation Professionals. Nanjing:ASCE, 2012. |
| [23] | 王福建, 韦薇, 王殿海, 等.基于宏观基本图的城市路网交通状态判别与监控[C]//第7届中国智能交通年会.北京:电子工业出版社, 2012. WANG Fu-jian, WEI Wei, WANG Dian-hai, et al. Urban Road Network Traffic State Identification and Monitoring Based on Macroscopic Fundamental Diagram[C]//The 7th China Intelligent Transportation Conference. Beijing:Publishing House of Electronics Industry, 2012. |
| [24] | KEYVAN-EKBATANI M, KOUVELAS A, PAPAMICHAIL I, et al. Exploiting the Fundamental Diagram of Urban Networks for Feedback-Based Gating[J]. Transportation Research Part B:Methodological, 2012, 46(10): 1393-1403 |
| [25] | TOSHIO Y, YUJI Y, KITAMURA R. Evaluation of an Area Metering Control Method Using the Macroscopic Fundamental Diagram[C]//The 12th World Conference on Transportation Research. Lisbon, Portugal:[s. n.], 2010. |
 2017, Vol. 34
2017, Vol. 34
