扩展功能
文章信息
- 孙祯, 上官萍, 卓卫东, 陈力波, 谷音
- SUN Zhen, SHANGGUAN Ping, ZHUO Wei-dong, CHEN Li-bo, GU Yin
- 抗震加固对简支旧桥地震易损性的影响
- Influence of Seismic Reinforcement on Fragility of Old Simply Supported Bridge
- 公路交通科技, 2017, 34(3): 87-93, 109
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(3): 87-93, 109
- 10.3969/j.issn.1002-0268.2017.03.012
-
文章历史
- 收稿日期: 2015-07-30
公路桥梁在抗震救灾中起关键作用,属“生命线工程”,但在《公路工程抗震设计规范》(JTJ 004-89) 出台之前设计的桥梁大多未进行抗震设计。随着我国进入地震活跃期[1],现有大批关键线路上的重要桥梁亟待加固。根据震害特点,针对下部结构 (墩柱) 和连接构件 (支座),采用墩柱钢套管加固、墩柱碳纤维加固、替换隔震支座等方案对桥梁进行抗震加固。如何在众多的抗震加固方案中选择出最优加固策略是关键,可通过对比加固前后的桥梁地震易损性曲线来实现。已有国外学者[2]对加固后的桥梁进行易损性分析,以对比各抗震加固方案对桥梁地震易损性的影响,而国内研究仅限于构件 (墩柱、支座) 和桥梁整体结构的地震易损性和参数敏感性分析,并未对采用不同方案加固后的桥梁进行易损性分析。因此,有必要针对各抗震加固方案对简支旧桥地震易损性的影响进行研究。
参考美国[3]和中国台湾地区的桥梁抗震加固规范和相关报告,建立加固桥梁的有限元模型并绘制桥梁加固前后的易损性曲线,选择能将桥梁结构的损伤概率降至最低的方案为最优抗震加固方案。该分析亦为抗震加固方案的风险分析和成本-收益分析提供了基础。
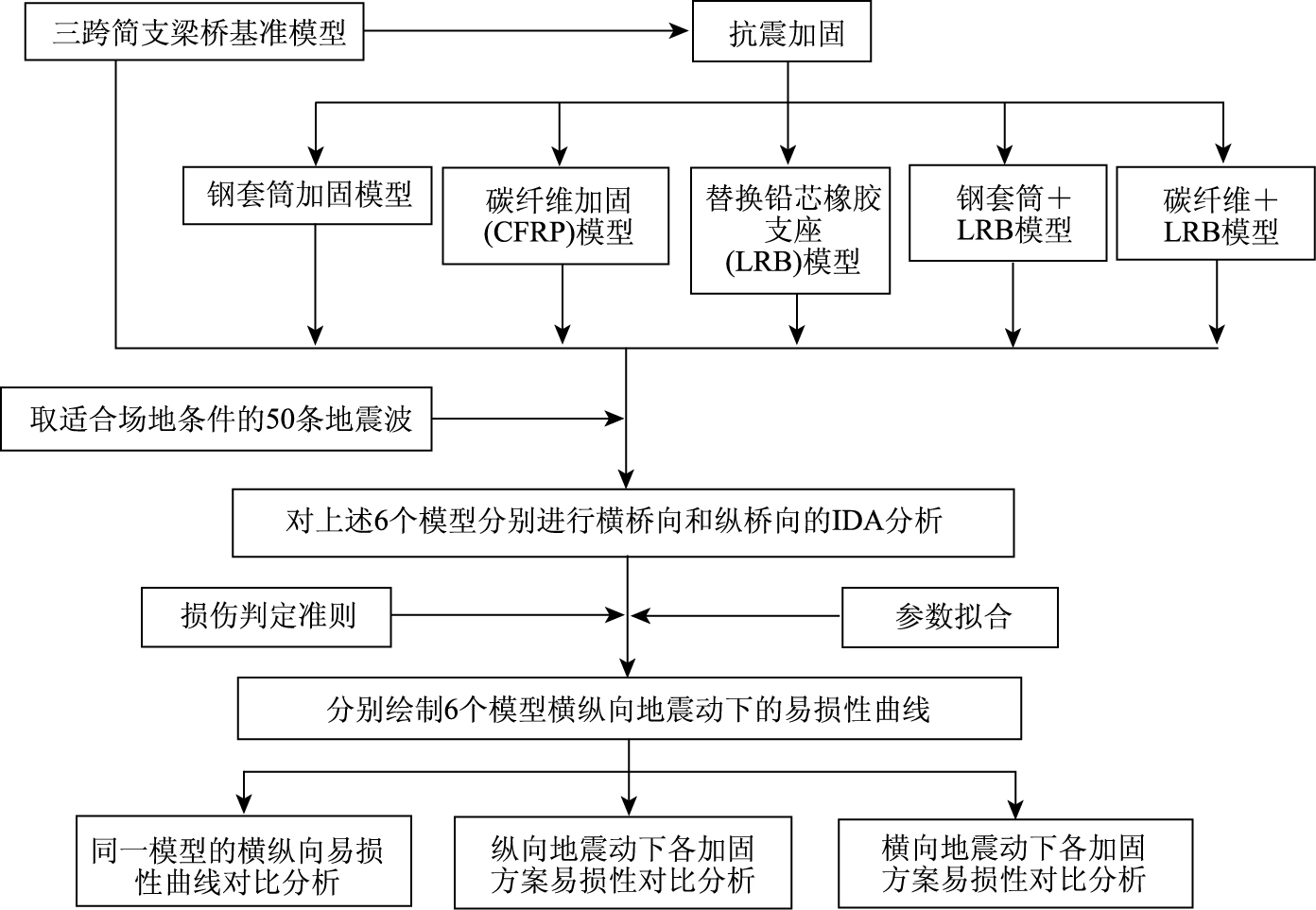
1 地震易损性分析流程地震易损性是指在不同水平地震动作用下,结构达到或超过某一极限损伤状态 (性能水平) 的超越概率。由于各种抗震加固策略未经过实际地震的检验, 难以通过经验统计回归分析的方法进行震害预测,因此宜采用理论易损性的分析方法,具体流程图如图 1所示。
|
| 图 1 抗震加固桥梁的地震易损性分析流程 Fig. 1 Process of fragility analysis for seismic retrofitted bridges |
| |
1.1 损伤指标的确定
墩柱损伤指标选择墩顶漂移率DR,是墩顶位移Δ与净墩高L的比值,DR=Δ/L×100%。对独柱墩L均取为桥墩墩高;对多柱墩,纵向时L为墩高,横向时L取墩顶到反弯点的距离。该指标直观性强, 可较好地反映结构构件的损伤程度,且相对于裂缝宽度、应变等性能指标的量测更为便捷,不会因为采用不同的方法定义屈服、极限位移而使得到的延性系数区别较大,减少了各种不确定性因素的影响。
支座损伤指标选容许剪切应变γa,是支座最大相对位移μmax与支座橡胶层总厚度∑te的比值。因其直接受剪切模量、橡胶层阻尼和支座尺寸的影响,故能更好地反映支座的性能。
桥梁结构系统的损伤指标。Jian Zhang等人[4]依据修复费用和承载能力对桥墩和隔震支座赋予不同的权重:在轻微、中等、严重破坏 (DS取1,2,3) 时,因为墩柱比支座具有更强的功能性且修复费用更高,故赋予桥墩破坏概率P(Fp) 的权重为0.75,赋予支座破坏概率P(Fb) 的权重为0.25;在完全破坏 (DS取4) 时,任何构件的损伤都可能导致桥梁系统的整体破坏,因此宜选择串联系统的概率结构,即桥梁结构系统的破坏概率等于最易破坏的构件的破坏概率。桥梁结构系统破坏状态如下:
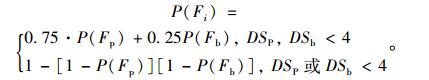
|
将桥墩和支座的损伤破坏等级分为4个等级,则墩柱和支座的各级损伤破坏指标[5-6]见表 1。
| 损伤破坏极限状态 | 破坏状态描述[7] | 量化描述 | |
| 墩柱漂移率DR/% | 支座剪切应变γa/% | ||
| 轻微破坏 | 微小裂缝和混凝土剥落,无需维修即可投入使用 | 0.41 < DR < 0.91 | 100 < γa < 150 |
| 中等破坏 | 中等裂缝和混凝土剥落,经一般维修可投入使用 | 0.91 < DR < 1.01 | 150 < γa < 200 |
| 严重破坏 | 严重退化但不至于倒塌危及生命安全,无修复价值 | 1.01 < DR < 2.20 | 200 < γa < 250 |
| 完全破坏 | 结构倒塌失效,完全丧失使用功能,无法修复 | DR>2.20 | γa>250 |
1.2 地震波的选取
以地震波的动力放大系数谱为基础,综合考虑场地类别、震中距、震级等因素,忽略桩土效应,从1971年San Fernando地震、1985年Michocan地震、1987年Whittier地震、Loma Prieta地震、1994年Northridge地震选取符合Ⅰ类场地特征的地震波共50条[8]。选取PGA作为地震动输入的强度指标。
1.3 绘制地震易损性曲线首先采用IDA分析方法,得到每条地震动激励下的墩顶最大位移以及支座最大相对位移;再利用损伤破坏指标与破坏等级之间的关系,获得每个损伤等级的发生概率;然后通过数据进行曲线拟合,得出易损性曲线[9]。
2 算例及非线性模型 2.1 基准模型据统计资料[10]:梁式桥中以简支梁桥震害最为严重。我国20世纪建造了大量简支梁桥,且多为跨径20~30 m的直线桥、板式橡胶支座、双柱墩。基于此,选取最具有代表性的漳州市第二通道大嵼林头大桥作为基准模型,截取其中三跨进行分析。该桥属桥面连续的简支T型梁桥,跨径组合为3×25 m,桥面总宽12 m,主梁采用C30混凝土;板式橡胶支座;桥墩采用C20混凝土, 截面直径1.2 m, 墩高7 m,双柱圆形墩; 纵筋为18根直径为25 mm的HRB235级钢筋,箍筋为直径为8 mm的HPB235级钢筋,箍筋间距为20 cm。该桥位于Ⅰ类场地。不考虑土与结构的相互作用,墩底固结处理。
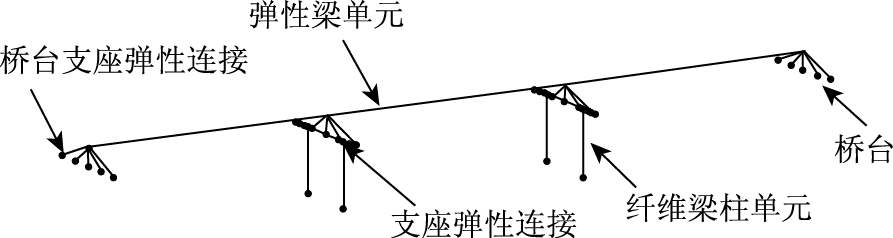
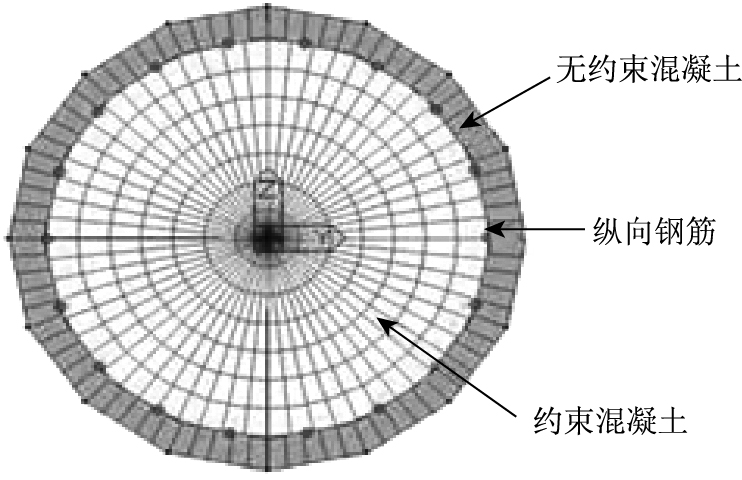
利用Midas/Civil软件建立桥梁非线性有限元分析模型见图 2。地震作用下,上部结构不易破坏,故采用弹性梁单元模拟;破坏主要集中在墩柱和支座,要求墩柱具有较大延性,抗震规范中允许桥墩在强震作用下出现塑性铰,故墩柱采用纤维截面模拟塑性铰,见图 3。混凝土保护层和约束混凝土用Mander模型,忽略混凝土的抗拉强度;钢筋采用对称的双折线钢筋模型,认为其受拉和受压性能相同。
|
| 图 2 简支桥梁有限元模型 Fig. 2 Finite element model of simply supported bridge |
| |
|
| 图 3 墩柱纤维截面划分 Fig. 3 Fiber section gridding of pier |
| |
板式橡胶支座类型为GJZ200×350,其恢复力模型近似为直线型,即可用弹性连接模拟,由代表 6个自由度方向的弹簧组成。依据《公路桥梁抗震设计细则》(JTG/T B02-01-2008) 求得支座竖向刚度为506 500.23 kN/m,水平向刚度为1 615.38 kN/m,转动刚度均取零。
2.2 钢套管加固钢套管加固是将两片钢板卷成半圆 (考虑到间隙,半径为墩柱半径再加13~15 mm),固定到待加固墩柱,再将两片钢板间的竖向焊缝焊接起来,钢板与混凝土圆柱表面之间填充水泥砂浆。该法旨在通过约束混凝土来提高其延性能力,类似钢筋混凝土柱中的箍筋[11]。钢管不直接承压以防止起到受压钢筋的作用,一般都是通过在钢套管与梁、钢套管与柱脚之间预留约50 mm的缝隙来实现的,如图 4所示。

|
| 图 4 钢套筒加固立面图和截面图 Fig. 4 Steel jacket retrofit details of full height and section |
| |
钢套管计算公式是基于美国联邦公路局 (FHWA) 编写的《公路结构物抗震加固手册:第一部分--桥梁》(FHWA-HRT-06-032) 和中国台湾编写的《公路桥梁耐震能力评估及补强准则之研究》进行的。由于钢套管的约束,混凝土纤维增加了抗压强度f′cc和极限应变εcc,可通过改变混凝土的Mander本构模型参数来对其进行模拟。径向约束应力f′l由箍筋改为钢套管提供:
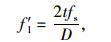
|
式中,t为钢套筒筒壁厚度;fs为钢套筒产生的应力;D为柱直径。
综上所述:确定建模所需参数的关键是钢套管的厚度tj,而钢套管的厚度又与其延性性能、抗剪性能、搭接补强和施工方便可操作这4项有关,接下来将着重研究钢套管厚度的计算方法。
(1) 从延性角度考虑钢套管厚度tj
依据Mander模型约束混凝土应力应变曲线,可得所需钢套管厚度为tj:
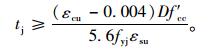
|
计算tj是一个不断迭代和分析的过程,初始代入的tj值一般偏于保守:先假设混凝土应变需求εcu为0.02、约束混凝土应力f′l需求为1.7 f′co,钢套管极限应变εsc于Q235取0.1。加固旧桥墩柱采用C20混凝土,其抗压强度f′co取为17,则求得厚度为9.743 mm。
(2) 从抗剪角度考虑钢套管厚度tj
参考《高速桥梁抗震设计》[13]对墩柱截面进行弯矩-曲率分析求得墩柱抗剪能力,并参考《桥梁延性抗震设计》[12]确定剪力需求,得出墩柱的抗剪能力和需求,见表 2。
| 抗剪能力 | 抗剪需求 | ||||||
| 参数 | 纵向 | 横向 | 参数 | 纵向 | 横向 | ||
| 初始 抗剪 |
Vci/kN | 1 081.84 | 1 081.84 | Mtzc/(kN·m) | - | 1 820.68 | |
| Vsi/kN | 142.17 | 142.17 | Mbzc/(kN·m) | 1 893.56 | 1 893.56 | ||
| Vpi/kN | 136.03 | 272.06 | Hn/m | 7 | 7 | ||
| Vni/kN | 1 360.04 | 1 496.07 | Voi/kN | 378.71 | 742.85 | ||
| 延性 抗剪 |
Vcd/kN | 373.05 | 373.05 | Mtzc/(kN·m) | - | 1 849.93 | |
| Vsd/kN | 142.17 | 142.17 | Mbzc/(kN·m) | 1 783.28 | 1 849.93 | ||
| Vpd/kN | 120.59 | 241.19 | Hn/m | 7 | 7 | ||
| Vnd/kN | 635.81 | 756.41 | Vod/kN | 369.99 | 726.64 | ||
| 注:表中Vni和Vnd分别表示脆性破坏和延性破坏时的抗剪能力, Vni=Vci+Vsi+Vpi, Vnd=Vcd+Vsd+Vpd;Voi和Vod表示脆性破坏和延性破坏时的抗剪需求;Vci和Vcd表示混凝土提供的抗剪强度;Vsi和Vsd表示钢筋提供的抗剪强度;Vpi和Vpd表示轴力提供的抗剪强度;Mtzc为柱顶截面正截面受弯承载力对应弯矩值;Mbzc为柱底截面正截面受弯承载力对应弯矩值;Hn为墩柱净长度。 | |||||||
由此可见,墩柱原本抗剪能力大于抗剪需求,因此不需要钢套管对其抗剪能力进行加固补强。
(3) 从搭接角度考虑钢套管厚度tj
虽然我国新规范对柱底塑性铰区内的钢筋做出了禁止搭接的要求,但旧桥却不可避免:柱底钢筋搭接使得钢筋加倍,屈服不显著,导致延性不佳。所需钢套管厚度为:
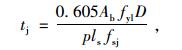
|
式中,Ab为单根圆柱主筋横截面积;fyl为主筋的屈服强度;fsj为钢套管材料的屈服强度;D为钢套管的直径;p为搭接钢筋发生劈裂后,一根钢筋外环绕裂缝的长度;ls为柱底钢筋搭接长度。可求得搭接加固时,钢套管最小厚度应为1.534 mm。
(4) 施工方便和可操作性
为了操作方便,钢板厚度应大于10 mm;由于厚板弯曲的限制,厚度不应超过25 mm。对于直径为1.2 m的旧桥墩柱,10 mm厚的Q235钢已足以提供足够的延性能力、抗剪能力和搭接加固补强。
综上所述,旧桥加固的钢套管厚度应选为10 mm,参考规范公式求得混凝土有效侧应力fl、约束混凝土的强度f′ccεcc,见表 3。
| 参数 | fl/MPa | f′cc/ MPa | εcc |
| 取值 | 3.333 | 33.287 | 0.011 581 |
2.3 碳纤维 (CFRP) 加固
纤维增强复合材料 (FRP) 是由纤维材料用环氧树脂等复合而成的高性能复合材料,质轻高强、加工方便,适于承受往复荷载、移动荷载作用的桥梁结构。碳纤维 (CFRP) 在工程应用中尤为常见[13]。CFRP贴布用环氧树脂紧贴于墩柱,不得与柱脚或柱顶接触,预留5 cm缝隙,其建模方法与钢套筒一致。
计算的碳纤维布均以日本某公司生产的UT70-30碳纤维布为准,设计厚度为0.167 mm,实测抗拉强度为4 223 MPa,抗拉弹性模量为243 000 MPa,则设计拉应变为0.017 3。
(1) 从延性角度考虑CFRP厚度tj
纤维复合材料贴布的计算与钢套筒类似,二者不同之处在于纤维复合材料贴布达到其拉力强度前,其应力应变关系属于线性,所需碳纤维布筒厚度tj公式变为:
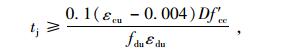
|
式中,f′cc取值同钢套筒,但其径向约束应力取为fl=2.07 MPa;εcu混凝土极限应变,取0.02;fdu为CFRP的设计抗拉强度,取4 223 MPa;εdu为CFRP的设计拉应变,取0.017 3,则厚度为0.788 mm。
(2) 从抗剪角度考虑CFRP厚度tj
墩柱原本抗剪能力大于抗剪需求,不需要CFRP对其抗剪能力进行加固。
(3) 从搭接角度考虑CFRP厚度tj
同钢套筒计算方法一样,CFRP布的最小厚度应为0.1 mm。
综合上述3个方面:碳纤维布的加固厚度应取0.788 mm,约为设计厚度的5倍,即需缠绕5层,厚度为0.835 mm,由此可得CFRP加固建模所需的参数,见表 4。
2.4 铅芯橡胶支座 (LRB) 替换
铅芯橡胶支座 (LRB-Lead Rubber Bearing) 是在叠层橡胶支座的基础上加入铅芯,使其具有更大的初始刚度与滞回耗能的能力。铅芯橡胶支座 (LRB) 支座轴向方向为单线性力学模型,其有效刚度取为支座的轴向刚度,非线性特性值的弹性刚度应与线性特性值中的有效刚度相同;水平剪切方向是双轴塑性,即双线性力学模型。Midas内置了铅芯橡胶支座的建模模块,确定支座种类和参数后可直接调用。参考《公路桥梁铅芯隔震橡胶支座》(JT/T822-2011) 和卓卫东等人[14]的研究成果,选择替换的支座类型为J4Q350×350。具体建模参数如下:
| 支座类型 | 水平等效刚度/(kN·m-1) | 竖向刚度/(kN·m-1) | 铅芯屈服力Qy/kN | 剪切弹模/MPa | 等效阻尼比ξ/% | 等效阻尼系数C | 刚度比γ |
| J4Q350×350 | 1 900 | 1 000 000 | 67 | 1.2 | 16.7 | 117.38 | 0.155 |
3 桥梁构件和结构易损性曲线 3.1 旧桥横纵向易损性曲线对比
将地震波分别从横桥向和纵桥向输入旧桥基准模型,计算并绘制墩柱、支座和桥梁结构的易损性曲线,见图 5。

|
| 图 5 基准模型在纵桥向和横桥向的地震易损性曲线 Fig. 5 Seismic fragility curves of benchmark model in longitudinal and transverse directions |
| |
对比图 5中旧桥基准模型的横、纵向易损性曲线,得出:(1) 桥墩在纵桥向发生轻微、中等和严重破坏的概率比横桥向更大,但发生完全破坏的概率比横桥向小;(2) 支座在横、纵桥向的易损性曲线相似;(3) 由于桥梁结构的易损性很大程度取决于墩柱,故桥梁结构易损性曲线的趋势与墩柱类似,即桥梁在纵桥向发生轻微、中等、严重破坏的概率比横桥向大,但发生完全破坏的概率比横桥向小。
3.2 各加固方案对构件、桥梁地震易损性的影响基于上述结果,针对更易发生破坏的纵桥向地震波输入情况进行研究,考虑5组抗震加固方案:钢套筒加固、碳纤维加固 (CFRP)、铅芯橡胶支座的替换 (LRB)、钢套筒加铅芯支座 (LRB+钢套筒) 和碳纤维加铅芯支座 (LRB+CFRP), 5组加固桥梁在轻微、中等、严重、完全破坏状态下的构件和结构易损性曲线见图 6。

|
| 图 6 各加固方案对桥墩、支座和桥梁易损性曲线的影响 Fig. 6 Influence of 5 retrofitting schemes on fragility curves of piers, bearing and bridge |
| |
对墩柱而言:(1) 钢套筒和CFRP加固在轻微、中等、严重破坏状态下对墩柱的破坏概率几乎没有影响,只有在完全破坏时才会较明显地降低墩柱的破坏概率;(2) LRB在各种破坏状态下均可较大幅度降低墩柱破坏概率;(3) 两种组合加固方案 (LRB+钢套筒、LRB+CFRP) 可使桥墩破坏概率下降最多,但当地面峰值加速度大于0.5g时,LRB使墩柱发生轻微破坏的概率下降最多。
对支座而言:(1) 墩柱加固后,支座的破坏概率会略有增加;(2) 铅芯橡胶支座 (LRB) 在各破坏状态下可最大程度降低支座破坏概率,而两种组合加固方案 (LRB+钢套筒、LRB+CFRP) 对支座破坏概率的降低程度较铅芯橡胶支座小,这是由加固墩柱后会增加支座的破坏概率所造成的。
对桥梁结构而言:(1) 对墩柱进行钢套筒和碳纤维加固,桥梁结构的破坏概率略有降低但不明显;(2) 铅芯橡胶支座 (LRB) 可显著降低桥梁结构在各破坏状态下的破坏概率;(3) 各加固方案对桥梁结构易损性降低的幅度从大到小依次为:LRB+CFRP、LRB+钢套筒、LRB、CFRP、钢套筒。
4 结论针对常见的典型简支旧桥,采用5种常见的抗震加固方案对其进行加固,并建立加固前后的桥梁有限元模型,经非线性时程分析绘制理论易损性曲线,分析了旧桥基准模型在横、纵桥向的破坏情况并对比了5个加固方案对构件和结构的易损性影响,结论如下:
(1) 对于桥墩,同时加固墩柱和替换支座能最大程度地降低桥墩发生各个破坏状态的概率。
(2) 对于支座,加固桥墩会使支座更易破坏,故替换铅芯橡胶支座可最大程度降低支座破坏概率。
(3) 对于桥梁结构,各加固方案降低桥梁易损性的程度由高到低依次为:铅芯橡胶支座加碳纤维、铅芯橡胶支座加钢套筒、铅芯橡胶支座、碳纤维、钢套筒。故在不考虑经济条件的情况下,采用铅芯橡胶支座加碳纤维的抗震加固方法可有效降低桥梁结构发生破坏的概率。
(4) 在选取地震波时仅考虑了Ⅰ类场地,而大量研究表明,不同场地的地震波频谱成分相差较大,而频谱成分将明显影响结构的地震响应,进而影响结构的易损性;且工程实际中有大量的桥梁位于I类、Ⅱ类, 甚至Ⅲ类场地上。因此在选取地震波时至少应选取Ⅰ类、Ⅱ类场地的地震波,最好包括Ⅲ类场地。
| [1] | PADGETT J E. Seismic Vulnerability Assessment of Retrofitted Bridges Using Probabilistic Methods[D]. Atlanta:Georgia Institute of Technology, 2007. |
| [2] | PADGETT J E. Seismic Vulnerability Assessment of Retrofitted Bridges Using Probabilistic Methods[D]. Atlanta:Georgia Institute of Technology, 2007. |
| [3] | FHWA-HRT-06-032, Seismic Retrofitting Manual for Highway Structures:Part1-Bridges[S]. |
| [4] | ZHANG Jian, HUO Yi-li. Evaluating Effectiveness and Optimum Design of Isolation Devices for Highway Bridges Using the Fragility Function Method[J]. Engineering Structures, 2009, 31(8): 1648-1660 |
| [5] | 邢文杰.规则桥梁概率地震需求与抗震能力研究[D].福州:福州大学, 2013:37-38. XING Wen-jie. Study on Probabilistic Seismic Demand and Capacity Analysis for Regular Bridges[D]. Fuzhou:Fuzhou University, 2013:37-38. |
| [6] | 陈力波.汶川地区公路桥梁地震易损性分析研究[D].成都:西南交通大学, 2012:83-84. CHEN Li-bo. Seismic Vulnerability Analysis for Highway Bridges in Wenchuan Region[D]. Chengdu:Southwest Jiaotong University, 2012:83-84. |
| [7] | Federal Emergency Management Agency. Multi-hazard Loss Estimation Methodology, Earthquake Model:HAZUS99 User's Manual[M]. Washington, D. C.:Federal Emergency Management Agency, 1999. |
| [8] | 吴少锋.独塔部分斜拉桥地震易损性分析[D].福州:福州大学, 2009. WU Shao-feng. Seismic Fragility Analysis of Extra-dosed Cable-stayed Bridge with Single-tower[D]. Fuzhou:Fuzhou University, 2009. |
| [9] | 张菊辉, 胡世德. 桥梁地震易损性分析的研究现状[J]. 结构工程师, 2005, 21(5): 76-80 ZHANG Ju-hui, HU Shi-de. State of the Art of Bridge Seismic Vulnerability Analysis Research[J]. Structural Engineers, 2005, 21(5): 76-80 |
| [10] | 游福科.在役公路混凝土梁式桥震害预测与抗震鉴定研究[D].福州:福州大学, 2011. YOU Fu-ke. Study on Damage Prediction and Identification of Seismic Performance for In-service Highway Concrete Beam Bridges[D]. Fuzhou:Fuzhou University, 2011. |
| [11] | 蔡健, 徐进. 圆形钢套管加固混凝土中长柱轴压承载力研究[J]. 铁道科学与工程学报, 2005, 2(4): 62-67 CAI Jian, XU Jin. Research on Bearing Capacity of Reinforced Concrete Column Strengthened by Circular Steel jacketing Subjected to Axial Loads[J]. Journal of Railway Science and Engineering, 2005, 2(4): 62-67 |
| [12] | 卓卫东, 范立础. 桥梁延性抗震设计[M]. 北京: 人民交通出版社, 2001: 197-198. ZHUO Wei-dong, FAN Li-chu. Bridge Ductility Seismic Design[M]. Beijing: China Communications Press, 2001: 197-198. |
| [13] | 范立础. 高架桥抗震设计[M]. 北京: 人民交通出版社, 2001. FAN Li-chu. Seismic Design of Elevated Bridge[M]. Beijing: China Communications Press, 2001. |
| [14] | 王吉忠, 王苏岩, 黄承逵. CFRP加固高强混凝土柱抗震性能和延性研究[J]. 大连理工大学学报, 2008, 48(5): 708-714 WANG Ji-zhong, WANG Su-yan, HUANG Cheng-kui. Research on Ductility and Earthquake-resistance of High-strength Concrete Column Confined by CFRP[J]. Journal of Dalian University of Technology, 2008, 48(5): 708-714 |
| [15] | 卓卫东, 孙颖, 谷音. 长大公路混凝土连续梁桥抗震方案比选[J]. 土木工程与管理学报, 2011, 28(3): 313-321 ZHUO Wei-dong, SUN Ying, GU Yin. Comparison of Seismic Design Schemes for Long-span Concrete Continuous Hhighway Girder Bridges[J]. Journal of Civil Engineering and Management, 2011, 28(3): 313-321 |
 2017, Vol. 34
2017, Vol. 34
