扩展功能
文章信息
- 张存超, 张士红, 郭晓光, 邵旭东
- ZHANG Cun-chao, ZHANG Shi-hong, GUO Xiao-guang, SHAO Xu-dong
- 轻型组合桥面板层间剪应力计算及栓钉连接件的布置设计
- Calculation of Interlaminar Shear Stress of Lightweight Composite Bridge and Preliminary Study on Layout Design of Stud Connectors
- 公路交通科技, 2017, 34(3): 62-69
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(3): 62-69
- 10.3969/j.issn.1002-0268.2017.03.009
-
文章历史
- 收稿日期: 2016-06-06
2. 湖南大学, 湖南 长沙 410082
2. Hunan University, Changsha Hunan 410082, China
由于沥青混凝土具有重量轻、变形协调性好、与钢桥面板黏着性能优越、易于维修以及行车舒适等优点,现代正交异性钢桥面板 (下文均简称“钢桥面板”) 一般均采用沥青混合料铺装[1]。工程实践表明[1-5],由于层间黏结力不足,沥青铺装易出现脱空、裂缝等病害。关于钢桥面板沥青铺装的层间应力计算,许多学者进了大量的研究:文献[2]基于具有特殊边界的叠层梁模型,推导了横向层间剪应力的解析计算公式;文献[4]采用有限元方法,分析了沥青铺装层间剪应力的影响因素,并拟合出层间应力计算公式;文献[5]基于正交试验方法分析了沥青的受力特性,结果表明,有限元模型的几何尺寸和边界条件对层间剪应力的大小几乎没有影响,并提出钢桥铺装计算分析的合理简化有限元模型。
为解决传统钢桥面板的铺装层易损及钢结构疲劳两大难题,文献[6-7]提出将具有高弹性模量 (E=42.6 GPa)、高抗拉强度 (>7 MPa) 的密实配筋UHPC层通过栓钉连接件与钢桥面板连接,形成新型的轻型组合桥面板结构。由于UHPC层与钢顶板的弹性模量差别较大,荷载作用下,层间同样会产生较大的剪应力。为保证UHPC层与钢顶板之间的有效黏结,工程实践中主要采用栓钉连接件来实现二者的共同受力[6]。目前,轻型组合桥面板中栓钉连接件的布置设计主要依赖粗糙的计算和工程经验,这可能会导致栓钉的数量和布置方式的不合理。另外,由于有限元计算结果与实际工程具有一一对应的特点,反复修改栓钉的布置方案会消耗大量的计算费用。为方便工程设计,本文以洞庭湖二桥为工程背景,在分析局部轮载荷位对层间剪应力影响的基础上,推导得到轻型组合桥面板横、纵向层间剪应力的解析计算公式,对轻型组合桥面板的层间剪应力计算和栓钉连接件的布置设计进行了初步的探究。
1 有限元分析研究表明[3],大跨径悬索桥的铺装层与钢顶板之间的层间剪应力主要受局部轮载的影响,整体效应的影响可忽略不计。为简化计算和抓住问题的主要方面,本文仅考虑局部轮载作用下UHPC层与钢顶板之间的层间剪应力计算。为方便后续分析,首先探究局部轮载荷位对层间剪应力的影响。
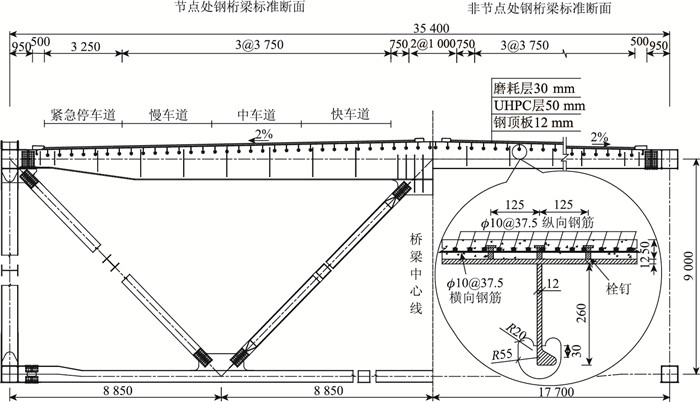
1.1 荷位对层间剪应力的影响 1.1.1 局部有限元模型以洞庭湖二桥为工程背景。洞庭湖二桥为双塔双跨钢桁梁悬索桥,垂跨比1/10,主跨1 480 m,全长2 390 m。初步设计方案中,加劲梁桁高9.0 m,桥面全宽35.4 m,钢桁梁顶板厚12 mm,横梁高1.38 m,横肋高0.75 m,每隔2.8 m设一道横梁或横肋,横隔板厚10 mm。纵肋采用HP260 mm×12 mm (高度×厚度) 的球扁钢,间距500 mm。钢顶板上焊上长35 mm、直径13 mm的材质为ML15A的栓钉,间距125×125 mm (纵向×横向)。然后再绑扎ϕ10的HRB335钢筋,其纵、横向间距均为37.5 cm,形成钢筋网。最后浇注50 mm厚的UHPC层,采用蒸汽养护,形成轻型组合桥面板结构,如图 1所示。
|
| 图 1 钢桁梁标准横断面图 (单位:mm) Fig. 1 Standard cross-section of steel truss girder (unit: mm) |
| |
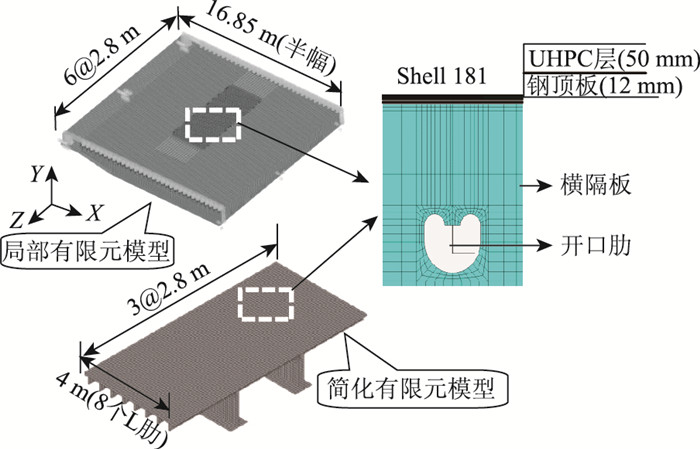
采用ANSYS有限元软件建立轻型组合桥面板的局部有限元模型[6-7]和简化有限元模型[5]。局部有限元模型纵向包括6跨横隔板间距长度,考虑到对称性,横向采用半幅结构;简化有限元模型为文献[5]推荐的钢桥铺装简化有限元分析模型--在整体钢箱梁模型的基础上,确定一个包含数个纵肋、横肋以及一定边界约束条件的小尺寸有限元模型,且能保证其计算结果与采用整体有限元模型的计算结果基本一致。本文的简化有限元模型纵向包括3跨横隔板长度,横向包括8个肋间距,横隔板高度为1.2 m,如图 2所示。
|
| 图 2 有限元模型 Fig. 2 Finite element model |
| |
两类有限元模型中,除钢顶外的其他钢板 (杨氏模量为2.1×105 MPa,泊松比为0.3) 均采用SHELL63模拟,UHPC (弹性模量为4.26×104 MPa,泊松比为0.2) 和钢顶板采用多层壳SHELL181单元模拟。SHELL181单元分为两层,上层为50 mm厚UHPC,下层为12 mm厚钢顶板。局部轮载作用下,UHPC与钢顶板之间的相对滑移很小,因此有限元分析中,假设UHPC层与钢顶板之间完全连续接触[8-9]。考虑到模型的规模较大,对关注局部区域的网格进行细化,其他区域采用较粗糙的网格。有限元计算前先进行了模型的敛散性分析,最终确定网格尺寸在10 mm左右,计算结果精度能满足要求。文献[8-9]采用与上述局部有限元模型相同的建模方式计算得到的轻型组合桥面板的各项力学指标与实测值吻合度极高,这在一定程度上佐证了采用上述局部有限元模型得到的计算结果能代表轻型组合桥面板层间剪应力实际值。
局部有限元模型的边界条件为[6-7]:在端横隔板截面处,约束端部的纵向 (Z向) 平动自由度和绕竖向 (Y向) 与横轴 (X向) 的转动自由度;在道路中心线截面处,采用横向 (X向) 对称约束;在有吊索位置的横隔板底板位置处约束其竖向 (Y向) 平动自由度;在桁架节点处,约束钢桁梁横隔板底板的全部自由度。
简化有限元模型的边界条件为[5]:纵边自由,横边简支,横隔板底固接。
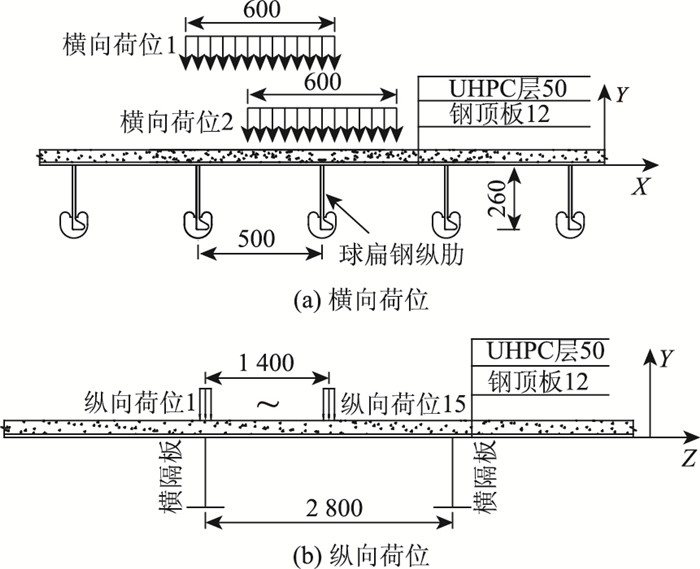
1.1.2 加载荷位及计算结果计算荷载采用《公路桥涵通用设计规范》[11]规定的车辆荷载 (轴重140 kN,单轮着地面积0.20 m×0.60 m)。考虑轮载与纵肋之间的相对位置,选择2个横向荷位,见图 3(a);考虑轮载与横隔板之间的相对位置,选择纵向间距为100 mm的共计15个纵向荷位,见图 3(b) 。计算得到2×15=30个荷载工况下的纵、横向层间剪应力最大值,见图 4。
|
| 图 3 加载荷位 (单位:mm) Fig. 3 Loading positions (unit:mm) |
| |

|
| 图 4 不同荷位层间剪应力计算结果 Fig. 4 Calculation result of interlaminar shear stresses at different wheel load positions |
| |
由图 4可知:(1) 不同纵向荷位时,两类有限元模型的计算结果差别小于1%。这表明,采用上述两类有限元模型的计算结果是等效的,与文献[5]的研究结果一致;(2) 除纵向荷位1~3外,纵向荷位的变化对横、纵向层间剪应力的影响较小;(3) 与横向荷位2相比,横向荷位1下的横向层间剪应力τxy大5%~18%,纵向层间剪应力τyz相差在±14%以下;(4) 除个别荷位外,同一荷位下的横向层间剪应力值较纵向层间剪应力大50%左右。
1.2 汽车制动力对层间剪应力的影响汽车在桥面行驶时,轮胎与路面之间会产生很大的水平力,水平荷载的计算公式[4]为:

|
(1) |
式中,T为水平荷载;P为车辆荷载;μ为制动系数,通常在0.3~1.0之间,这里取汽车紧急制动的最不利情况,即μ=0.5。
在局部有限元模型的基础上,在局部轮载作用位置建立表面效应单元SURF154,并施加水平汽车荷载T。计算得到汽车制动作用力下,纵、横桥向层间剪应力分别为τTL=0.055 MPa和τTH=0.071 MPa。可见,汽车制动力对轻型组合桥面板层间剪应力的影响在4%左右,可忽略不计。
2 层间剪应力计算 2.1 横向层间剪应力计算根据前文分析可知,横向层间剪应力峰值的计算荷位可取横向荷位1,纵向荷位15的轮载位置组合。将轻型组合桥面板简化成连续弹性支撑在纵肋上的叠层梁,称为计算模型1,如图 5所示,其中,Ln为纵肋间距;Kn为纵肋对叠层梁的当量支承刚度;hs为钢顶板厚度;hc为UHPC层的厚度。

|
| 图 5 计算模型1 Fig. 5 Computational model 1 |
| |
文献[2]提出了钢桥面板沥青铺装的层间剪应力计算模型,即具有特殊边界条件的简支叠层梁模型,并基于这一简化计算模型,推导得到了层间剪应力的解析计算公式。本文基于文献[2]的计算思想,将计算模型1也简化为具有特殊边界条件的简支叠层梁模型,即计算模型2,见图 6。由于约束了支座位移,同时忽略了其他部分的横向约束,则基于计算模型2得到的横向层间剪应力较计算模型1的偏大,计算结果偏安全。

|
| 图 6 计算模型2 Fig. 6 Computational model 2 |
| |
基于计算模型2,可推导得到宽度为b的叠层梁层间最大剪应力的解析计算公式,见式 (2),具体的推导过程在文献[2]中已有详述,本文不再赘述:

|
(2) |
其中,q为轮载荷载集度;a为叠层梁的中心轴与界面之间的距离,满足:
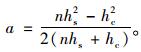
|
(3) |
I为叠层梁的惯性矩 (单位宽度),即:

|
(4) |
式中,n=Es/Ec,其中,Es为钢的弹性模量,Ec为UHPC的弹性模量。
以洞庭湖二桥轻型组合桥面板工程为例。车辆荷载同前述,即有q=140×103÷2÷0.6=116 666 N/m。考虑到轻型组合桥面板的双向传力作用,本文对文献[2]中简支叠层梁模型直接取轮载的纵向长度作为板计算长度的方法进行修正,这里板的纵向计算长度取轻型组合桥面板的有效宽度。基于最不利荷位,轮载作用下板的有效分布宽度可近似参考《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD62-2004)[13]计算,即取b=(0.2+0.5)/3=0.366 7 m。横桥向计算宽度考虑L=0.5 m的肋间轮载的计算,分布在肋外的轮载,对跨中弯矩起到减小作用,因此这样的计算结果偏于保守。
将n=Es/Ec=206 GPa/42.6 GPa=4.84,hs=12 mm,hc=50 mm,代入式 (3) 可得a=-8.34 mm。
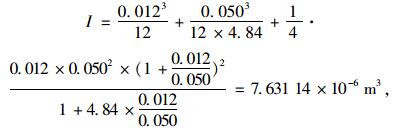
|
将上述数据代入式 (2) 中,可得:

|
局部有限元模型计算得到局部轮载作用下横向层间剪应力为1.743 MPa,基于本文修正的简支叠层梁模型计算方法得到的解析值比有限元值大1.5%,可见解析值比有限元结果偏安全。采用文献[2]的计算方法,轻型组合桥面板的纵向计算长度取荷载的实际长度b=0.2 m,代入式 (2) 可得横向层间剪应力解析值为3.289 MPa。此时,基于文献[2]的简支叠层梁模型计算方法得到的横向层间剪应力解析值比有限元值大88.7%,与有限元值偏差较大。
2.2 纵向层间剪应力计算根据前文的分析可知,纵向层间剪应力峰值的计算荷位可取横向荷位1、纵向荷位2的轮载位置组合。将轻型组合桥面板简化成连续弹性支撑在横肋上的叠层梁,称为计算模型3,如图 7所示。其中,Kn为横梁的当量支撑刚度,Ln为横梁间距。

|
| 图 7 计算模型3 Fig. 7 Computational model 3 |
| |
由于横梁间距较大,而轮载纵向分布宽度仅为l=0.2 m左右,可将计算模型3进一步简化为计算模型4,即悬臂叠层梁模型,见图 8。由于忽略了其他部分的纵向约束,采用计算模型4得到的横向层间剪应力较计算模型3的偏大,偏安全。

|
| 图 8 计算模型4 Fig. 8 Computational model 4 |
| |
采用材料力学方法,基于计算模型4推导得到宽度为b的叠层梁层间最大剪应力的解析计算公式:

|
(5) |
式中,S0为上结构层对整个截面的面积矩;b为板的有效分布宽度;F为悬臂承受的荷载值,F=ql。
基于最不利荷位,横桥向计算宽度考虑L=0.5 m的肋间轮载的计算,即有b=L=0.5 m。取F=140×103÷2÷0.6×0.5=58 333 N,b=0. 5 m,S0=1.721 074 3×10-4 m4,代入式 (5) 可得:

|
局部有限元计算得到局部轮载作用下纵向层间剪应力为1.830 MPa,解析计算值比有限元值大30.4%,可见解析计算值比有限元结果偏安全。
3 栓钉连接件的布置设计在得到层间剪应力的基础上,可偏安全地以最大层间剪应力进行栓钉连接件的布置设计。假设纵向栓钉间距为uL,横向栓钉间距为uH,则一个栓钉连接件承受的剪力Vsd应小于其承载力值[Pu],需满足:
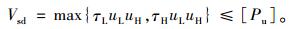
|
(6) |
可先假定横向栓钉的间距uH,然后代入式 (6) 中即可确定纵向栓钉的间距uL。
参考文献[13]可知,UHPC薄层中直径13 mm,高35 mm,材质为ML15A的栓钉接件的承载力值为[Pu]=51.6 kN。假设横向栓钉的间距uH=125 mm,将前文数据代入式 (6) 可得:uL≤245 mm。同时为方便施工,最终拟定纵、横桥向栓钉的间距取值相同,即uH=uL=125 mm。此时,栓钉连接件的最大剪力值为:
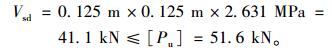
|
(7) |
由于解析计算公式是基于简化计算模型得到,层间剪应力有限元值比解析值偏小8.8%~38.6%,因而采用125 mm×125 mm (横向×纵向) 的栓钉布置方案是偏安全的,能满足洞庭湖二桥轻型组合桥面板的层间抗剪要求。一方面,Wang[15]的研究指出,工作状态下栓钉连接件受到的荷载一般约为0.5倍的承载力设计值。这就意味着,工作状态下的栓钉连接件,除局部区域的少数外,剪力值普遍处于较低水平。另一方面,栓钉受力不仅要满足静力承载力的要求,还需要满足疲劳要求。我国《钢-混凝土组合桥梁设计规范》(GB50917-2013)[16]规定工程构件中栓钉连接件疲劳剪力幅不大于0.2倍的抗剪承载力设计值。因此从栓钉连接件抗疲劳的角度出发,应采用偏保守的计算方法。
在初步确定栓钉的布置后,还需建立带栓钉连接件且考虑层间滑移的组合桥面板有限元模型,进行栓钉承载力和疲劳强度两方面的验算,具体方法可参考文献[14],反复修改栓钉连接件的布置方案,直至满足栓钉的承载力和疲劳强度两方面的要求为止。
4 进一步的分析由前文分析可知,局部轮载下轻型组合桥面板的横向层间剪应力基本对栓钉连接件的布置设计起控制作用。在实际工程中,为方便施工和设计,栓钉连接件通常采用等间距布置,且纵、横向连接件的间距保持一致,即uL=uH=s。因而可将问题进一步简化,在栓钉连接件初步布置设计中,可仅考虑局部轮载作用下栓钉连接件沿横桥向的布置设计。
假设UHPC层与钢顶板之间仅靠栓钉连接件提供层间抗剪作用,而UHPC层与钢顶板之间光滑无摩擦。将采用栓钉连接件进行层间抗剪的轻型组合桥面板简化成计算模型5,见图 9。考虑到轻型组合桥面板的局部刚度较大,纵桥向选取长度为b=0.366 7 m,横桥向选取一个肋间距的组合板段进行研究,其他字符含义同前述。由前文分析可知,采用计算模型5得到的栓钉连接件剪力值也是偏保守的。

|
| 图 9 计算模型5 Fig. 9 Computational model 5 |
| |
研究轻型组合桥面板条的i-1断面,该断面的轴向力为Ni-1, i,上、下板条中的弯矩Mi-1, i1(x),Mi-1, i2(x),则组合板条的i-1断面满足弯矩满足平衡条件:
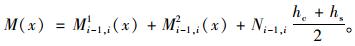
|
(8) |
分析i和i-1断面之间的板条。由于栓钉连接件的作用,UHPC层的下表面总变形与钢顶板上表面总变形相等,即满足变形条件。其中,UHPC层的下表面应变εi-1, i1(x)和钢顶板上表面的应变εi-1, i2(x)为:

|
(9) |
栓钉i和栓钉i-1之间的UHPC层下表面伸长量和钢顶板上表面伸长量相等,满足:

|
(10) |
另外,UHPC层与钢顶板的曲率半径相等,即满足物理条件:

|
(11) |
对于计算模型5,均布荷载作用下,距离端部x断面的弯矩大小为:

|
(12) |
联立式 (8)、(11) 可得:

|
(13) |
将式 (9)、(13) 代入式 (10) 中,可得断面i和i-1之间的剪力Ni-1, i:

|
(14) |
同理,可得断面i+1和i之间的剪力Ni, i+1:

|
(15) |
由式 (14)、(15) 可得第i个断面的总的剪力Qi:

|
(16) |
由式 (16) 可知,越靠近支座端部位置的断面的剪力越大。由于选取的板条宽度b已知,且uL=uH=s,即可得到i截面上栓钉连接件的个数为Nnum=
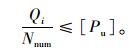
|
(17) |
由式 (17) 即可确定栓钉连接件的横向布置间距s。
对于端部位置有栓钉连接件的情况,可由式 (9) 得:

|
(18) |
即得端部位置栓钉连接件的剪力值Qn:

|
(19) |
对于洞庭湖二桥轻型组合桥面板工程,栓钉连接件采用125 mm×125 mm (横向×纵向) 的布置方案来说,s=125 mm,L=500 mm,长度b=0.366 7 m的板条上一个截面上的栓钉个数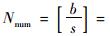


|
(20) |
式 (20) 计算表明,洞庭湖二桥轻型组合桥面板的栓钉连接件布置方式满足栓钉连接件的承载力要求。
5 结论轻型组合桥面板是为解决传统钢桥面的铺装层易损和钢结构疲劳两大难题而提出的高性能组合结构,UHPC层与钢顶板的界面有效抗剪是轻型组合桥面板结构发挥有效作用的关键,需重点关注。本文基于洞庭湖二桥轻型组合桥面板工程,在分析局部轮载对轻型组合桥面板层间剪应力影响的基础上,提出了纵向层间剪应力的简化计算模型--悬臂叠层梁模型,并基于轻型组合桥面板的受力特点,修正了文献[2]中基于简支叠层梁模型的横向层间剪应力计算中对板的计算长度取值。在简化计算模型的基础上,得到轻型组合桥面板层间剪应力的解析计算公式。基于工程实例的计算表明,采用文献[2]简支叠层梁模型的计算方法得到的横向层间剪应力解析值比有限元值大88.7%,而采用本文修正的简支叠层梁模型计算方法得到的解析值比有限元值仅大1.5%,计算精度有较大提高;纵向层间剪应力解析公式计算值比有限元值大30.4%左右,均偏保守。最后,进一步提出了栓钉连接件布置设计的简化计算模型。本文所给出的计算模型可为轻型组合桥面板的层间剪应力计算及栓钉连接件的布置设计提供参考。
| [1] | 黄卫. 大跨径桥梁钢桥面铺装设计理论与方法[M]. 北京: 中国建筑工业出版社, 2006. HUANG Wei. Theory and Method of Steel Deck Paving Design for Long-span Bridges[M]. Beijing: China Architecture and Building Press, 2006. |
| [2] | 赵锋军, 李宇峙, 易伟建. 桥面沥青铺装层间应力分析简化模型[J]. 土木工程学报, 2007, 40(6): 100-104 ZHAO Feng-jun, LI Yu-zhi, YI Wei-jian. A Simplified Model for Interlaminar Stress Analysis of Bridge Asphalt Pavement[J]. China Civil Engineering Journal, 2007, 40(6): 100-104 |
| [3] | 赵锋军.大跨径钢箱梁桥面沥青铺装设计方法研究[D].长沙:湖南大学, 2012. ZHAO Feng-jun. Research on Design Method for Steel Deck Asphalt Pavement on Large-span Steel Box Beam Bridges[D]. Changsha:Hunan University, 2012. |
| [4] | 顾兴宇, 吴一鸣. 钢桥桥面铺装层间剪应力影响因素及简化计算[J]. 交通运输工程学报, 2007, 7(3): 70-75 GU Xing-yu, WU Yi-ming. Influence Factors and Simplified Calculation of Interbedded Shear Stress of Asphalt Paving on Steel Bridge[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 70-75 |
| [5] | 邓强民, 倪富健, 顾兴宇, 等. 大跨钢桥桥面铺装有限元分析合理简化模型[J]. 交通运输工程学报, 2008, 8(2): 53-58 DENG Qiang-min, NI Fu-jian, GU Xing-yu, et al. Rational Simplified Model of Finite Element Analysis for Deck Pavement of Long-span Steel Bridge[J]. Journal of Traffic and Transportation Engineering, 2008, 8(2): 53-58 |
| [6] | SHAO Xu-dong, YI Du-tao, HUANG Zheng-yu, et al. Basic Performance of the Composite Deck System Composed of Orthotropic Steel Deck and Ultrathin RPC Layer[J]. Journal of Bridge Engineering, 2013, 18(5): 417-428 |
| [7] | ZHANG Shi-hong, SHAO Xu-dong, CAO Jun-hui, et al. Fatigue Performance of a Lightweight Composite Bridge Deck with Open Ribs[J]. Journal of Bridge Engineering, 2016, 21(7): 04016039 |
| [8] | 李嘉, 冯啸天, 邵旭东, 等. STC钢桥面铺装新体系的力学计算与实桥试验对比分析[J]. 中国公路学报, 2014, 27(3): 39-44 LI Jia, FENG Xiao-tian, SHAO Xu-dong, et al. Comparison of Mechanical Calculation and Actual Test for New STC Steel Bridge Paving System[J]. China Journal of Highway and Transport, 2014, 27(3): 39-44 |
| [9] | 李嘉, 王懿, 李洪, 等. 超高性能轻型组合桥面铺装体系基本力学性能研究[J]. 公路交通科技, 2015, 32(7): 55-61 LI Jia, WANG Yi, LI Hong, et al. Research on Basic Mechanical Property of Super High-performance Lightweight Composite Deck Pavement System[J]. Journal of Highway and Transportation Research and Development, 2015, 32(7): 55-61 |
| [10] | 邵旭东, 周环宇, 曹君辉. 钢-薄层RPC组合桥面结构栓钉的抗剪性能[J]. 公路交通科技, 2013, 30(4): 34-39 SHAO Xu-dong, ZHOU Huan-yu, CAO Jun-hui. Shear Behavior of Studs of Composite Deck System Composed of Steel and Ultra-thin RPC Layer[J]. Journal of Highway and Transportation Research and Development, 2013, 30(4): 34-39 |
| [11] | JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D50-2006, General Specification for Design of Highway Bridge and Culverts[S]. |
| [12] | 张起森, 李雪莲, 查旭东. 黄河二桥系杆拱桥桥面铺装结构力学性能研究[J]. 土木工程学报, 2006, 39(7): 88-93 ZHANG Qi-sen, LI Xue-lian, ZHA Xu-dong. Structural Mechanics Study of Tied Arch Bridge Deck Overlays of the Second Huanghe Bridge[J]. China Civil Engineering Journal, 2006, 39(7): 88-93 |
| [13] | JTG D62-2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62-2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [14] | 张士红, 邵旭东, 黄细军, 等. 轻型组合桥面板中小栓钉连接件的静力及疲劳性能研究[J]. 公路交通科技, 2016, 33(11): 41-49 ZHANG Shi-hong, SHAO Xu-dong, HUANG Xi-jun, et al. Static and Fatigue Behavior of Small Stud Shear Connector for Lightweight Composite Bridge Deck[J]. Journal of Highway and Transportation Research and Development, 2016, 33(11): 41-49 |
| [15] | WANG Y C. Deflection of Steel-Concrete Composite Beams with Partial Shear Interaction[J]. Journal of Structural Engineering, 1998, 124(10): 1159-1165 |
| [16] | GB 50917-2013, 钢-混凝土组合桥梁设计规范[S]. GB 50917-2013, Code for Design of Steel and Concrete Composite Bridges[S]. |
 2017, Vol. 34
2017, Vol. 34
