扩展功能
文章信息
- 霍学晋, 程曦
- HUO Xue-jin, CHENG Xi
- 钢-混结合段的极限承载力研究
- Study on Ultimate Bearing Capacity of Steel-concrete Composite Segment
- 公路交通科技, 2017, 34(3): 52-61
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(3): 52-61
- 10.3969/j.issn.1002-0268.2017.03.008
-
文章历史
- 收稿日期: 2015-10-08
2. 清华大学 土木水利学院, 北京 100084
2. School of Civil Engineering, Tsinghua University, Beijing 100084, China
钢-混凝土混合结构具有诸多优点,其工程应用日益增多,而作为关键构件的钢-混结合段,目前针对其设计方法和传力机理的研究明显滞后,严重制约着混合结构在大跨度桥梁中的推广和应用。关于钢-混组合结构极限承载力的研究多针对各类剪力连接件,研究方法也以推出试验为主[1-10],而对整个钢-混结合段极限承载力的研究还较少。由于受力过程中,格室钢板对填充混凝土产生约束,且钢板与混凝土间存在接触摩擦,使得推出试验的结果并不能完全反映结合段的真实受力情况。
为了解结合段构造的极限承载力,本文选取一个格室采用ABAQUS软件建立精细有限元模型,考虑材料非线性和剪力钉的非线性荷载滑移关系及格室内混凝土的开裂和压碎,对4种不同构造的单格室模型进行非线性全过程分析,研究了3种传力构件 (承压板、PBL连接件、剪力钉) 的传力比例及共同工作性能,并分析了格室内各构件在加载过程中的破坏顺序及最终的破坏形态。
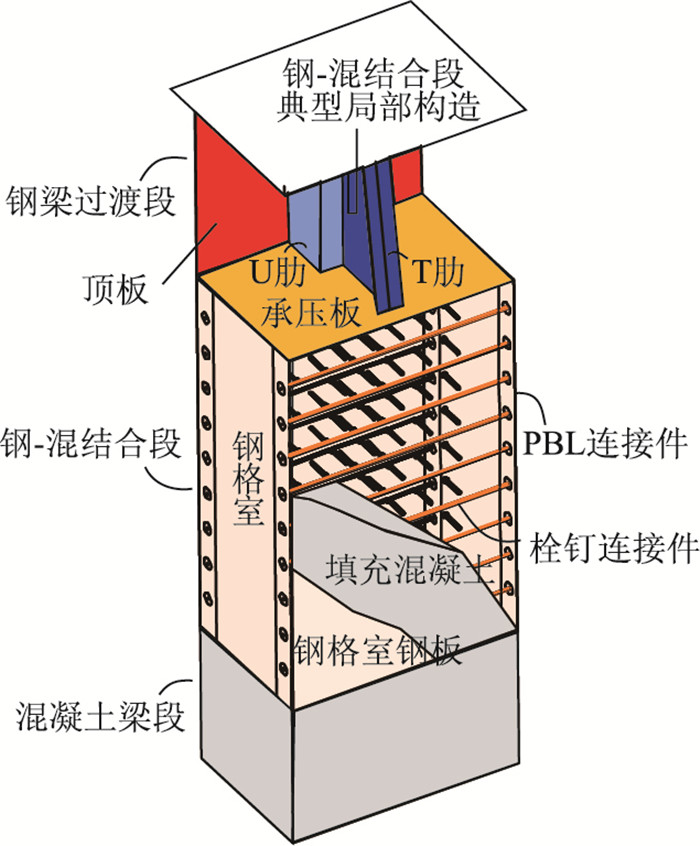
1 工程背景重庆永川长江大桥主桥为主跨608 m的7跨连续半漂浮体系的双塔混合梁斜拉桥。主梁为混合结构,中跨采用PK断面钢箱梁,边跨采用同外形的PK断面预应力混凝土箱梁,钢箱梁和混凝土箱梁通过钢-混结合段连接。该桥的钢-混结合段靠近主塔根部,承受主跨传来的较大轴力和弯矩。主梁钢-混结合段采用带格室的后承压板形式,具体构造:采用带T型加劲的U肋,钢箱梁端部设置多格室结构,且在格室内填充混凝土,并通过剪力键及钢板与混凝土间的黏结摩阻力传力,同时,在钢格室腹板上设置PBL剪力键。典型的钢-混结合段局部构造如图 1所示。
|
| 图 1 钢-混结合段的局部构造 Fig. 1 Local structure of steel-concrete composite segment |
| |
2 有限元模型的建立 2.1 单元的选择
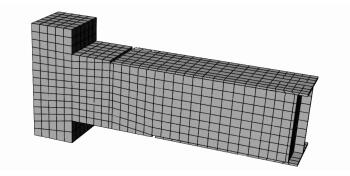
外钢板、PBL腹板、承压板、加载工字钢及格室混凝土和基座均采用实体单元C3D8R模拟,单元尺寸设为80 mm,对于形状规则的钢板如外钢板和承压板采用结构化网格划分技术,对于PBL腹板采用自由划分的方式,由于开孔钢板圆孔及连通孔处受力复杂,对其周围网格进行了加密。钢筋混凝土构件采用分离式模型模拟,普通钢筋采用杆单元T3D2模拟,PBL贯穿钢筋采用梁单元B31模拟,钢筋嵌入混凝土内,钢筋节点通过与相邻混凝土节点进行插值建立位移关系。剪力钉采用一维弹簧单元模拟,剪力钉的抗拔作用采用线性弹簧单元模拟,抗剪作用采用非线性弹簧单元模拟。有限元模型如图 2所示。
|
| 图 2 单格室的有限元模型 Fig. 2 Finite element model of sigle cell |
| |
2.2 边界条件
基座底面完全固结,PBL腹板与两侧混凝土间设置横向约束,避免互相穿透,采用硬接触模拟,不考虑腹板端部与混凝土之间的相互挤压作用。4种不同的构件,约束关系不同,考虑承压板的作用时采用节点耦合的方式模拟,无PBL的情况不考虑PBL贯穿钢筋的嵌入和开孔面上钢板与混凝土的约束关系,无剪力钉的情况在模型中取消弹簧单元,具体如表 1所示。为便于收敛,端部轴力以均布荷载的形式施加在加载端面上。
| 构件编号 | 承压板 | PBL贯穿钢筋 | 开孔 | 剪力钉 |
| 1 | 耦合 | 嵌入 | 接触 | 弹簧单元 |
| 2 | 不耦合 | 嵌入 | 接触 | 弹簧单元 |
| 3 | 不耦合 | 嵌入 | 接触 | 无弹簧单元 |
| 4 | 不耦合 | 不嵌入 | 不接触 | 弹簧单元 |
2.3 材料特性
(1) 混凝土材料
根据《混凝土结构设计规范》(GB 50010-2002),模型中取混凝土立方体抗压强度标准值fcu, k为50 MPa,单轴抗压强度fc为23.1 MPa,单轴抗拉强度ft为1.89 MPa,张开裂缝的剪力传递系数βt取0.5,闭合裂缝的剪力传递系数βc取0.95,拉应力释放系数取0.6。混凝土单轴应力应变关系上升段采用GB 50010-2002规定的公式,下降段则采用Hongnestad的处理方法,即:
当εc≤ε0时:
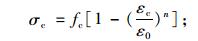
|
(1) |
当ε0<εc≤εcu时:
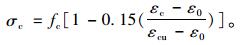
|
(2) |
按规范可取n=2, ε0=0.002, εcu=0.003 3,上述曲线可用一系列数据点拟合以便输入。
(2) 钢板和钢筋
钢板和钢筋的应力应变关系采用理想弹塑性模型,本文采用双线性随动强化模型,钢筋采用双线性等向强化模型模拟。
(3) 弹簧单元
剪力钉连接件为柔性连接件,在界面水平剪力作用下,不可避免地要发生界面滑移。纵向通过弹簧单元连接,弹簧单元模拟纵桥向连接件的抗剪刚度,单个剪力钉连接件的抗剪刚度采用《公路钢混凝土组合桥梁设计与施工规范》[11]中规定的方法进行计算:
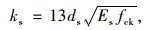
|
(3) |
式中,ks为剪力钉连接件的抗剪刚度;ds为剪力钉连接件的直径;fck为混凝土轴心抗压强度标准值;Ec为混凝土弹性模量。
圆柱头剪力钉的剪力-滑移曲线采用Ollgaard等人于1971年提出的本构关系[12]:
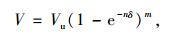
|
(4) |
式中,V为剪力钉承担的剪力;δ为界面滑移;n和m为常数,本文取m=0.558,n=1 mm-1;Vu为单个剪力钉的极限抗剪承载力,按式 (5) 计算[12]。
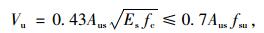
|
(5) |
式中,fcu为剪力钉材料极限抗拉强度;Aus为剪力钉截面积;Ec=105/(2.2+33/fcu);fc>=0.76fcu。
2.4 收敛条件求解采用Newton-Raphson法,将荷载分为100个增量步,每个增量步中设置迭代步,迭代收敛后,进入下一个增量步。计算中设置了双重收敛条件,残余力容差取为平均内力的0.05%,在残余力容差满足收敛条件后,检查位移增量是否小于总位移的0.1%。
3 不同构件的极限承载力分析 3.1 模型1的极限承载力模型1为原设计形式,主要目的是研究在设计构造形式下单个格室的极限承载力及受力状态。
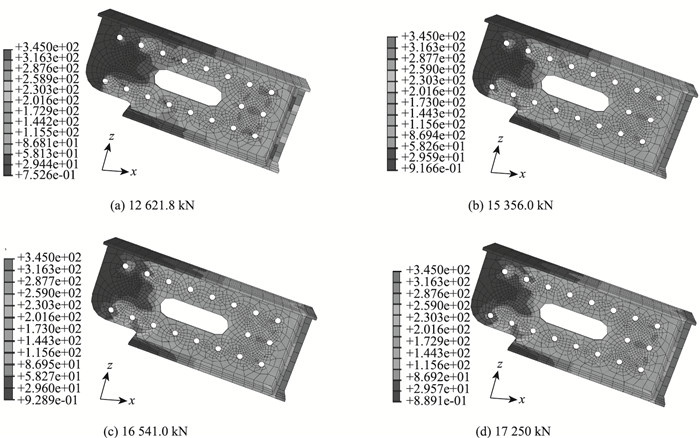
3.1.1 受力过程分析图 3示出了格室钢腹板在各加载阶段的应力分布情况。腹板的Mises应力刚达到屈服值345 MPa时的应力分布如图 3(a)所示,可见腹板最开始的屈服点出现在远离承压板的下端PBL开孔处,屈服荷载为12 621.8 kN,这时钢板大部分区域的应力均较低。由图 3(a)~(d)可见,随着荷载的增大,屈服区域并没有较大的扩展,仍集中在远端的上下开孔处,而格室外侧加载板的应力逐渐增大而趋于屈服,即构件的薄弱环节已转移至格室外。图 3(d)表明,在加载的极限荷载下,格室腹板仍保持较好的受力状态,可见原设计可承受更大的荷载,具有足够的安全储备。
|
| 图 3 格室腹板的应力分布 Fig. 3 Stress distribution of cell web |
| |
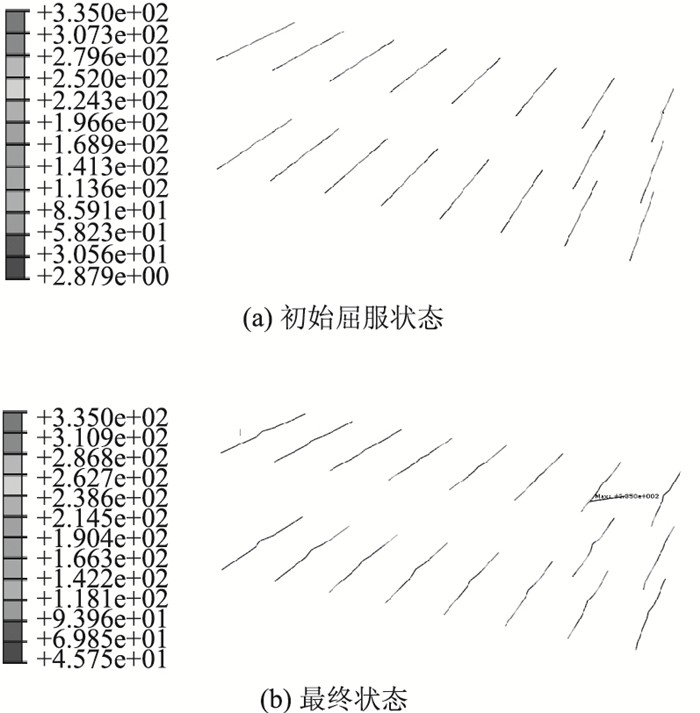
图 4示出了PBL贯穿钢筋在刚出现应力屈服和加载极限值时的应力分布。由图 4可见,PBL贯穿钢筋首先在靠近承压板的位置屈服,而加载极限状态时,由于应力重分布,各钢筋基本上都进入了屈服阶段,尤其在远离承压板侧。
|
| 图 4 不同阶段PBL贯穿钢筋的受力状态 Fig. 4 Stress states of PBL reinforced bar in different stages |
| |
3.1.2 PBL钢筋的屈服荷载
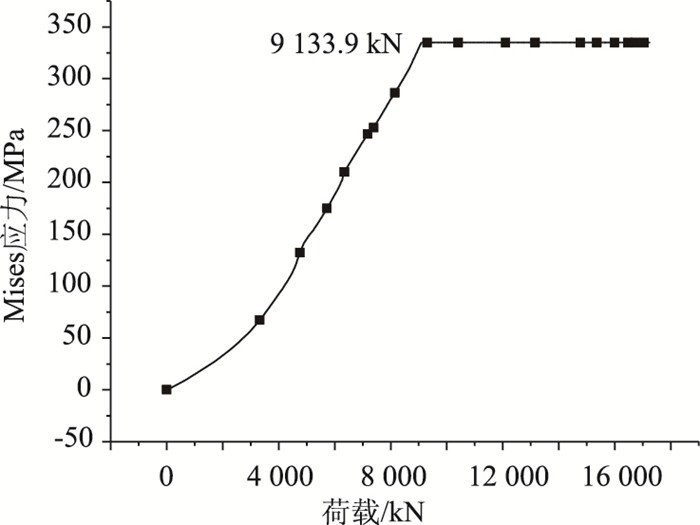
由图 4可见,PBL钢筋首先在靠近承压板的上端开孔处出现屈服。图 5示出了PBL贯穿钢筋首先屈服点的荷载应力曲线。由图 5可见,PBL钢筋的屈服荷载为9 133.9 kN。
|
| 图 5 PBL贯穿钢筋荷载应力曲线 Fig. 5 Load-stress curve of PBL reinforced bar |
| |
3.1.3 相对滑移量
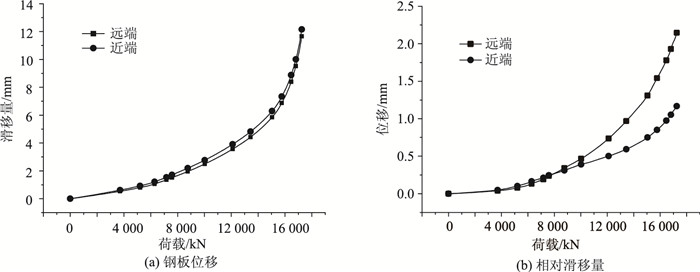
图 6示出了顶板剪力钉处钢板的位移和相对滑移量,图中远端和近端均相对于承压板而言。由图 6(a)可见,远端点和近端点的位移差别很小;由图 6 (b) 可见,在荷载较小时,远端点和近端点的相对滑移量相差不大,而随着荷载的增大,远端点的相对滑移量较近端点要大,且差值越来越大。由图 6可见,位移和相对滑移量曲线均呈现出明显的非线性特点。
|
| 图 6 钢板的位移和相对滑移量 Fig. 6 Displacement and relative slippage of steel plate |
| |
3.2 模型2的极限承载力
模型2不考虑承压板的承压传力作用,主要目的是研究PBL连接件和剪力钉在传力过程中的作用及各构件的受力全过程。
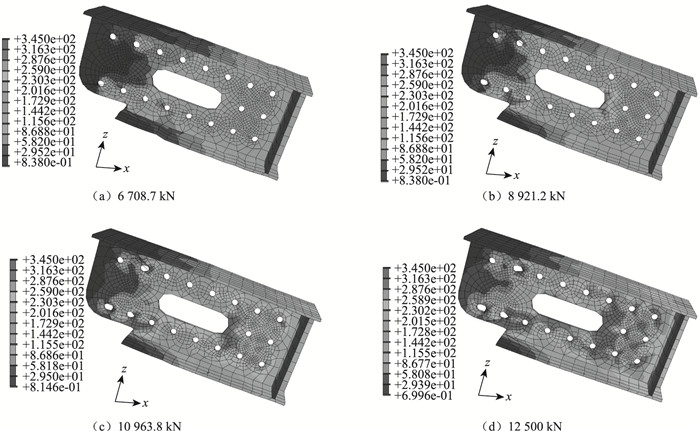
3.2.1 受力过程分析图 7示出了格室钢腹板在各加载阶段的应力分布情况,腹板的Mises应力刚达到屈服值345 MPa时的应力分布如图 7(a)所示,可见腹板最开始的屈服点仍出现在远离承压板的下端PBL开孔处,屈服荷载为6 708.7 kN,这时钢板大部分区域的应力均较低。由图 7(a)~(d)可见,随着荷载的增加,屈服的区域由远端的PBL开孔处向承压板方向扩展,上下端第2个PBL开孔及连通孔在承压板侧均出现了明显的屈服,直到屈服区域满布整个腹板。
|
| 图 7 格室腹板的应力分布 Fig. 7 Stress distribution of cell web |
| |
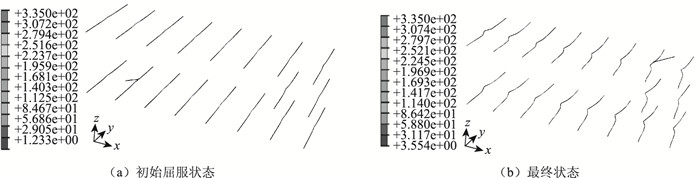
图 8示出了PBL贯穿钢筋在刚出现应力屈服和加载极限值时的应力分布。由图 8可见,PBL贯穿钢筋首先在靠近承压板的位置屈服,而加载极限状态时,由于应力重分布,各钢筋基本上都进入了屈服阶段,尤其在远离承压板侧。
|
| 图 8 不同阶段PBL贯穿钢筋的受力状态 Fig. 8 Stress states of PBL reinforced bar in different stages |
| |
3.2.2 PBL钢筋的屈服荷载
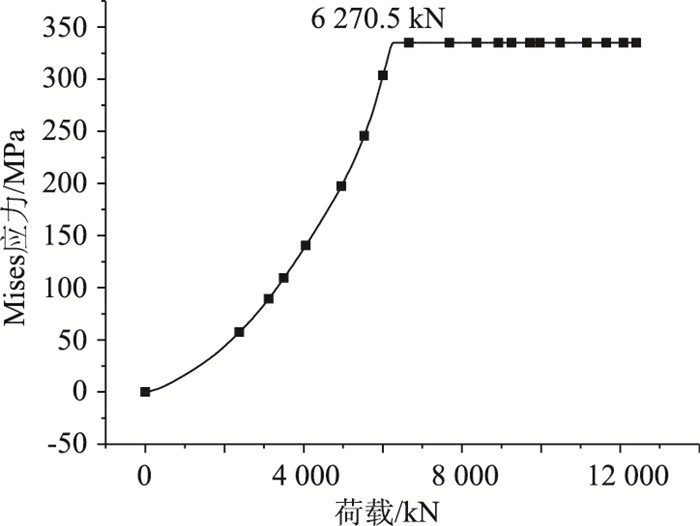
图 8表明PBL钢筋首先在远离承压板的上端开孔处屈服。图 9为PBL贯穿钢筋首先屈服点的荷载应力曲线,PBL钢筋的屈服荷载为6 270.5 kN。
|
| 图 9 PBL贯穿钢筋的荷载应力曲线 Fig. 9 Load-stress curve of PBL reinforced bar |
| |
3.2.3 相对滑移量
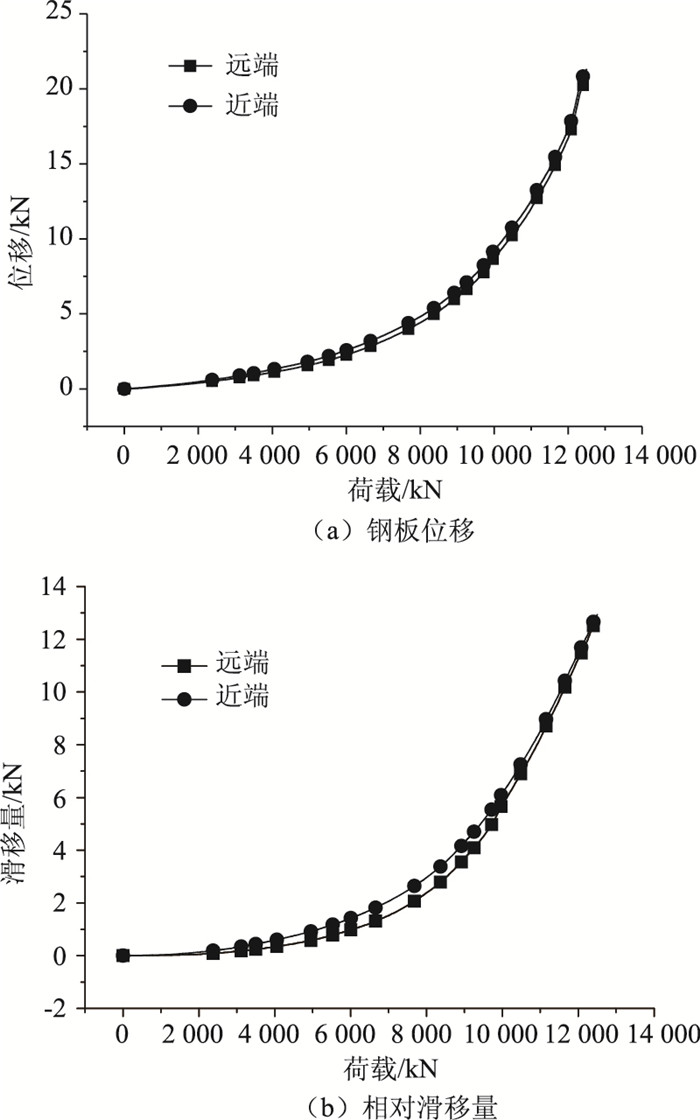
图 10示出顶板剪力钉处钢板的位移和相对滑移量。由图 10(a)可见,远端点的位移略大于近端点,整体上两者相差不大,而由图 10(b)可见,在荷载相对较小时,远端点的相对滑移量相差较大,随着荷载的增大,两者逐渐趋于一致,表明在临近破坏时,各剪力连接件的受力状态趋于相同。由图 10可见,位移和相对滑移量曲线均呈现出明显的非线性特点。
|
| 图 10 钢板的位移和相对滑移量 Fig. 10 Displacement and relative slippage of steel plate |
| |
3.3 模型3的极限承载力
模型3在模型2的基础上取消剪力钉的作用,既不考虑承压板的承压作用也不考虑剪力钉的传剪作用,主要目的是研究PBL连接件在传力过程中的作用及各构件的受力全过程。
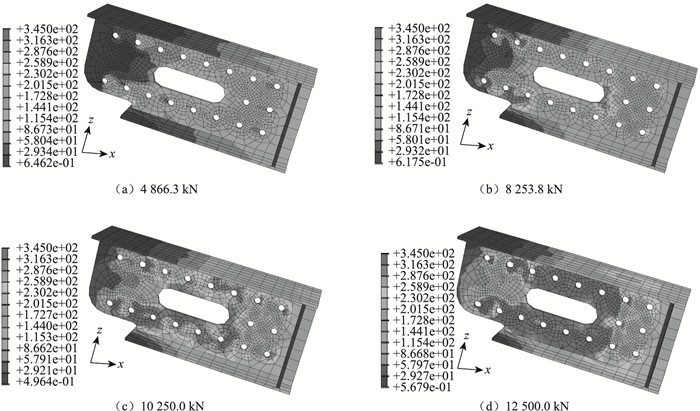
3.3.1 受力过程分析图 11(a)示出了腹板的Mises应力刚达到屈服值345 MPa时的应力分布,可见腹板最开始的屈服点仍出现在远离承压板的下端PBL开孔处,屈服荷载为4 866.3 kN,这时钢板大部分区域的应力均较低。由图 11可见,随着荷载的增加,屈服的区域由远端的PBL开孔处向承压板方向扩展,下端远端两个PBL开孔和上端第2个PBL开孔及连通孔在承压板侧均出现了明显的屈服。随着荷载的增大,屈服区域逐渐增大,在加载的极限荷载下,第2列PBL开孔以外的腹板基本上都处于屈服状态。
|
| 图 11 格室腹板的应力分布 Fig. 11 Stress distribution of cell web |
| |
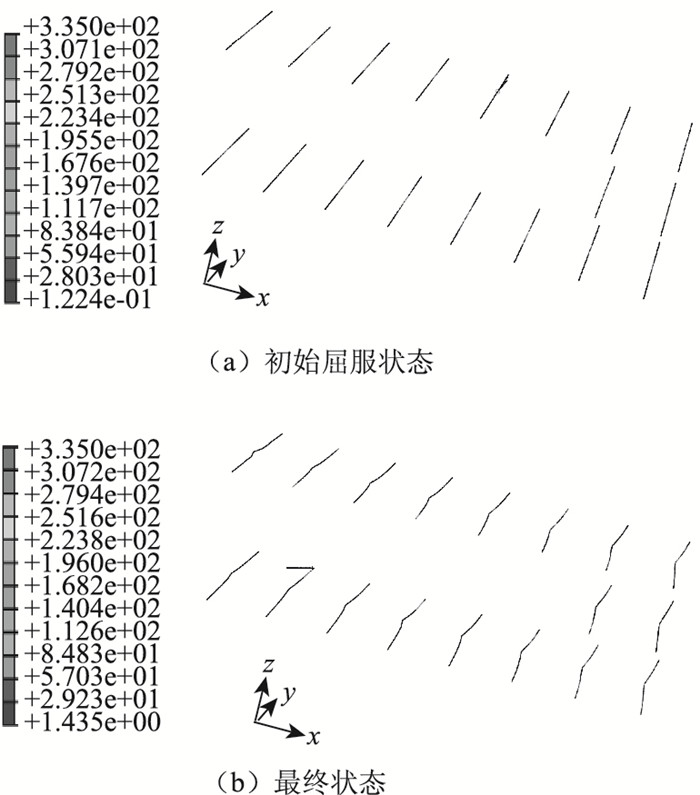
图 12示出了PBL贯穿钢筋在刚出现应力屈服和加载极限值时的应力分布。由图 12可见,PBL贯穿钢筋首先在腹板中部屈服,而加载极限状态时,由于应力重分布,大部分钢筋都进入了屈服阶段,但靠近承压板的一列贯穿钢筋尚未完全屈服,这与腹板的屈服状态是一致的。
|
| 图 12 不同阶段PBL贯穿钢筋的受力状态 (单位:MPa) Fig. 12 Stress states of PBL reinforced bar in different stages (unit:MPa) |
| |
3.3.2 PBL钢筋的屈服荷载
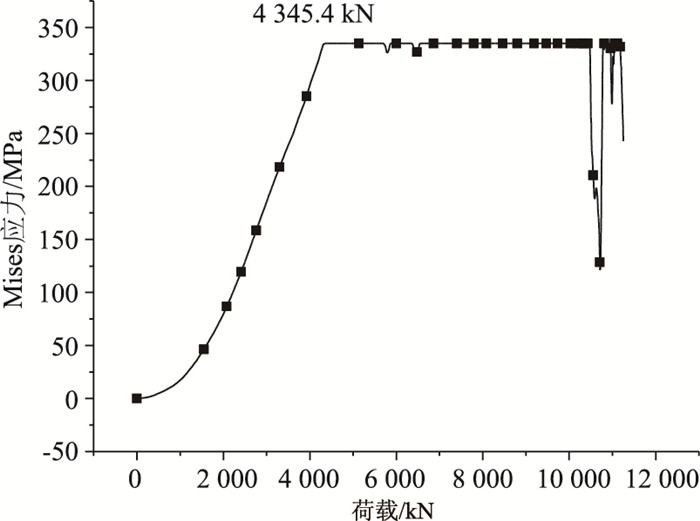
图 12表明PBL钢筋首先在远离承压板的上端开孔处屈服。图 13示出PBL贯穿钢筋首先屈服点的荷载应力曲线。由图 13可见,PBL钢筋的屈服荷载为4 345.4 kN,可见PBL钢筋的屈服荷载较低,在荷载较小时,某些贯穿钢筋就出现受剪屈服。
|
| 图 13 PBL贯穿钢筋荷载应力曲线 Fig. 13 Load-stress curve of PBL reinforced bar |
| |
3.3.3 相对滑移量
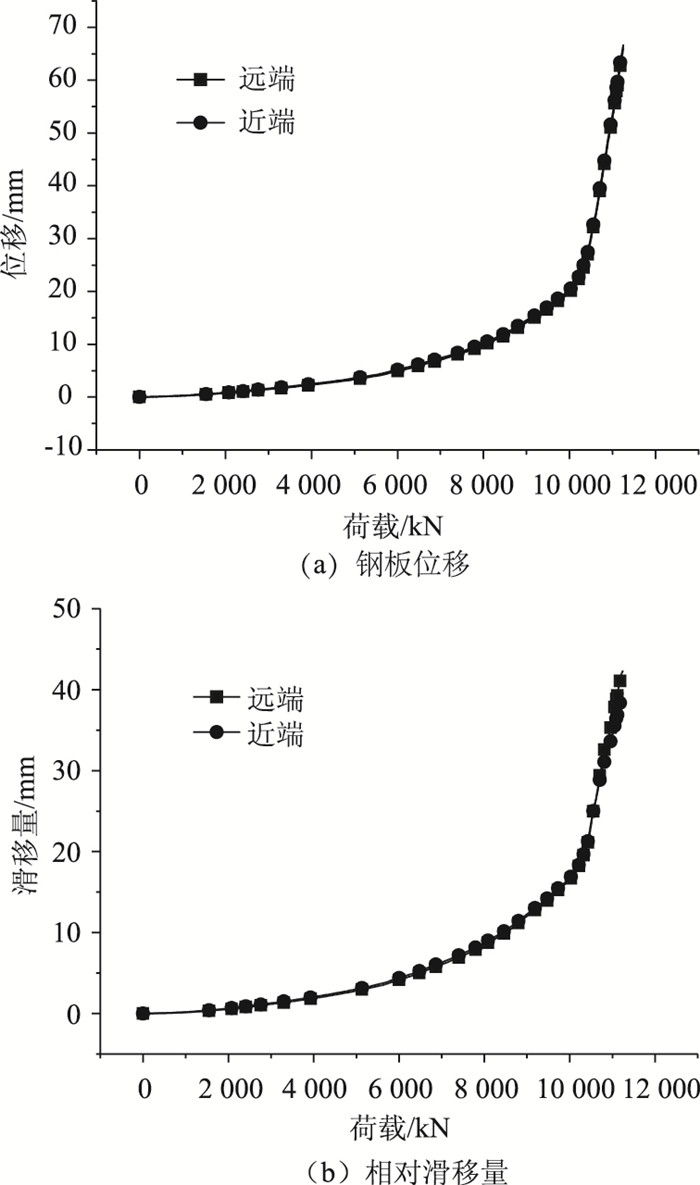
图 14示出了顶板剪力钉处钢板的位移和相对滑移量。由图 14可见,远端点和近端点的位移和相对滑移量均相差很小,几乎完全一致。
|
| 图 14 钢板的位移和相对滑移量 Fig. 14 Displacement and relative slippage of steel plate |
| |
3.4 模型4的极限承载力
模型4只考虑剪力钉的传剪作用,主要目的是研究剪力钉在传力过程中的作用及各构件的受力全过程。
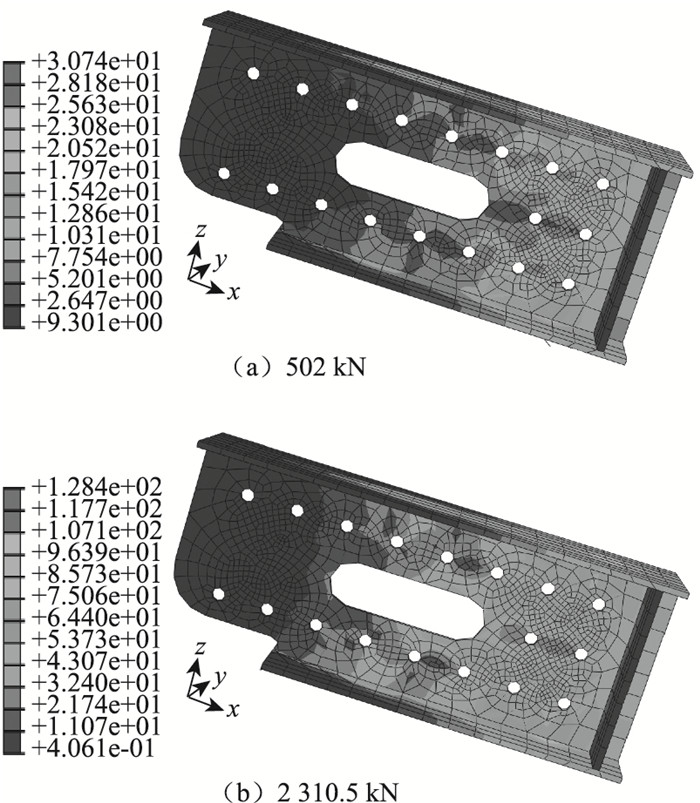
3.4.1 受力过程分析图 15示出了格室钢腹板在各加载阶段的应力分布情况。由图 15可见,在整个加载过程中,腹板的应力均较小,未出现屈服现象,应力较大点出现在顶板上靠近承压板的剪力钉处。由于只有剪力钉传力,极限荷载只能达到2 310.5 kN,荷载较小,因此各板件的应力水平均较低。
|
| 图 15 格室腹板的应力分布 Fig. 15 Stress distribution of cell web |
| |
3.4.2 相对滑移量
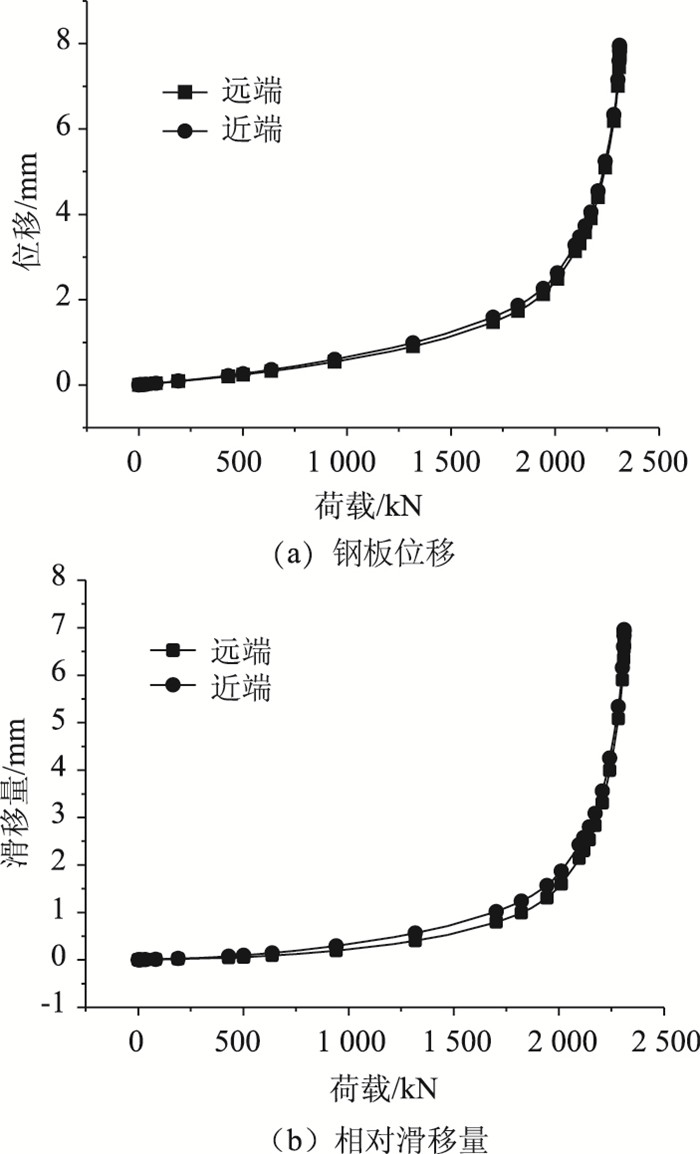
图 16示出了顶板剪力钉处钢板的位移和相对滑移量。由图 16可见,整体上,远端点和近端点的位移和滑移量基本一致,近端点的位移和滑移量略大于远端点。由图 16还可看出,当荷载增大到一定程度,位移和滑移量的曲线接近竖直,表明结构已失去了承载能力。
|
| 图 16 钢板的位移和相对滑移量 Fig. 16 Displacement and relative slippage of steel plate |
| |
3.5 四种模型的比较 3.5.1 受力状态的对比
对比图 3、图 7、图 11和图 15可见,4种模型的受力过程和破坏形态各不相同。考虑承压板作用的模型1中腹板的屈服区域随着荷载的增大并未明显扩大,当荷载达到17 250 kN时,屈服区域仍较小,构件的薄弱部分为格室外的加载板;不考虑承压板作用的模型2中腹板的屈服区域随着荷载的增大而明显扩大,最终状态为屈服区域散布整个腹板。在模型2的基础上去掉剪力钉的作用即模型3,腹板的屈服区域连成一片,且集中在第2列PBL开孔的外侧,第2列PBL开孔与承压板之间的腹板并未屈服;只考虑剪力钉作用的模型4,腹板的应力较小,并未出现屈服现象。
对比图 4(a)、图 8(a)和图 12(a)可见,3种模型中PBL贯穿钢筋首先出现屈服的位置并不相同。模型1中,靠近承压板的PBL贯穿钢筋首先屈服,这是由于承压板的传力作用,格室内混凝土直接承受较大的力,而中间腹板上的开孔对混凝土存在约束作用,使得端部的PBL贯穿钢筋受力较大。模型2中,远离承压板的PBL贯穿钢筋首先屈服,这是由于取消承压板的直接传力作用后,钢板在外荷载的作用下发生位移,该位移首先在远离承压板的端部受到混凝土块的约束,且该区域无剪力钉分担剪力,使得该处开孔的钢筋首先屈服。模型3中,既无承压板也无剪力钉,就使得各PBL贯穿钢筋的受力相差不大,相对较为均匀,另外由于连通孔的作用,在连通孔和承压板之间的区域,PBL贯穿钢筋的受力相对较小。
对比图 4(b)、图 8(b)和图 12(b)可见,3种模型的极限状态下PBL钢筋的受力状态基本一致,且各排钢筋的受力整体上趋于均匀。
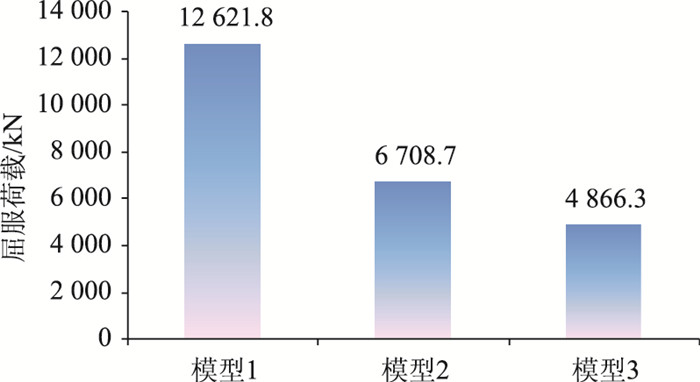
3.5.2 屈服荷载的比较图 17和图 18分别示出了钢腹板、PBL贯穿钢筋和混凝土内普通钢筋在不同构造形式下的屈服荷载。
|
| 图 17 钢板的屈服荷载 Fig. 17 Yield load of steel plate |
| |
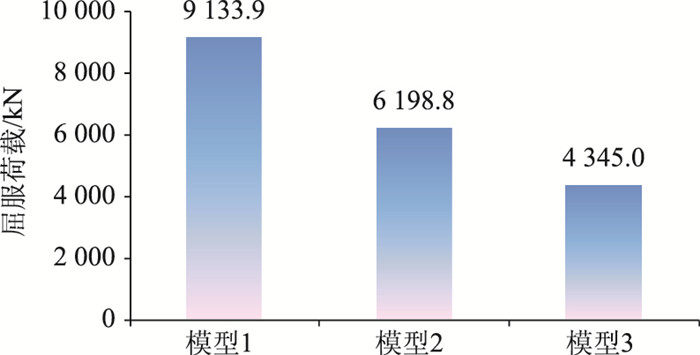
|
| 图 18 PBL贯穿钢筋的屈服荷载 Fig. 18 Yield load of PBL reinforced bar |
| |
由图 17可见,考虑承压板的承压作用后,钢腹板的屈服荷载要远大于无承压板模型,模型1相对模型2,屈服荷载提高了近一倍;而不考虑剪力钉的传剪作用后,模型3相对模型2,屈服荷载减小了27.5%。可见,剪力钉的设置可有效地提高钢板的屈服荷载,而承压板的作用更加明显。
由图 18可见,相比只有PBL连接件的模型3,增加剪力钉后模型2中PBL贯穿钢筋的屈服荷载提高了42.7%;相对模型2,增加承压板的作用后模型1中PBL贯穿钢筋的屈服荷载提高了47.4%。由此可见,剪力钉和承压板均能分担部分剪力,有效地提高了PBL钢筋的屈服荷载。
由图 19可见,剪力钉使得U筋在局部受压屈服,因此模型2相对模型3的屈服荷载降低,但由于钢筋屈服后会出现应力重分布,结构整体的承载力并未降低。
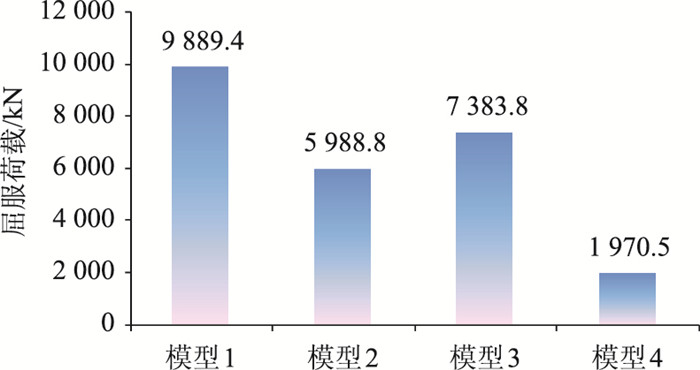
|
| 图 19 普通钢筋的屈服荷载 Fig. 19 Yield load of common steel bar |
| |
3.5.3 位移的比较
对比图 6、图 10、图 14和图 16可见,有承压板的情况下,随着荷载的增大远离承压板点和靠近承压板点的位移相差越大,而没有承压板的情况下,两者相差很小,尤其模型3,在只有PBL连接件时,两者几乎完全一致,这是由于模型3不考虑剪力钉的传剪作用以及钢板与混凝土间的摩阻力,外钢板只通过与腹板间的剪切作用传力,而模型3中腹板的变形也较为均匀,使得两者差别很小。
对比图 6、图 10、图 14和图 16还可看出,在荷载较大时,随着传力构件的减小,滑移量曲线的斜率逐渐趋于竖直。模型1在荷载达到16 000 kN时,滑移量曲线的斜率仍未接近竖直,可见该构件仍能承受更大的荷载;模型2在荷载达到12 000 kN时,仍可继续承担荷载;模型3当荷载为11 000 kN时,荷载-滑移量曲线接近竖直;模型4中,当荷载为2 250 kN时,荷载-滑移量曲线已接近竖直,构件失去了承载能力。由此可见,传力构件越多,构件的极限承载力越大,安全储备也越高,剪力钉的承载能力较低,可作为安全储备。
4 结论本文选取单个格室采用ABAQUS软件建立精细有限元模型,对4种不同构造的单格室模型进行非线性全过程分析,研究了3种传力构件的传力比例及共同工作性能。得到如下主要结论:
(1) 对于原设计构件,随着荷载的增大,腹板的屈服区域并没有较大的扩展,仍集中在远端的上下开孔处,而格室外侧加载板的应力逐渐增大而趋于屈服。
(2) 4种模型的受力过程和破坏形态各不相同,考虑承压板作用的模型1中腹板的屈服区域随着荷载的增大并未明显扩大,荷载达到17 250 kN时,屈服区域仍较小;不考虑承压板作用的模型2中腹板的屈服区域随着荷载的增大而明显扩大,最终状态为屈服区域散布整个腹板;无剪力钉的模型3,腹板的屈服区域连成一片,且集中在第2列PBL开孔的外侧;只考虑剪力钉作用的模型4,腹板的应力较小,并未出现屈服现象。
(3) 在荷载较大时,随着传力构件的减小,滑移量曲线的斜率逐渐趋于竖直。
(4) 3种传力构件中,承压板的直接承压作用能够有效地提高构件的极限承载力;有剪力钉的区域PBL钢筋和钢腹板的应力均相对较小,可见剪力钉能够有效地分担部分荷载,起到传力的作用;只有PBL连接件的情况下,各连接件的受力较为均匀。
| [1] | 吴文明.大跨度钢箱拱桥钢与混凝土结合部试验研究[D].上海:同济大学, 2007. WU Wen-ming. Experimental Research of Joint between Steel-concrete Arch Rib for Long Span Steel Box Arch Bridge[D]. Shanghai:Tongji University, 2007. |
| [2] | 黄彩萍.混合梁斜拉桥钢-混结合段受力性能的试验研究与理论分析[D].武汉:华中科技大学, 2012. HUANG Cai-ping. Experimental Study and Theoretical Analysis of Mechanical Behavior of Steel-concrete Joint Section of Hybrid Girder Cable-stayed Bridge[D]. Wuhan:Huazhong University of Science and Technology, 2012. |
| [3] | 张喜刚, 吴文明, 刘高. 无格式-承压板钢-混凝土结合部力学模型及简化计算方法[J]. 公路交通科技, 2013, 30(10): 49-53 ZHANG Xi-gang, WU Wen-ming, LIU Gao. Mechanical Model and Simplified Calculation Method of Steel-Concrete Connection Joint with Full-Connection Bearing-plates[J]. Journal of Highway and Transportation Research and Development, 2013, 30(10): 49-53 |
| [4] | 张清华, 李乔, 唐亮. 桥塔钢-混凝土结合段剪力键破坏机理及极限承载力[J]. 中国公路学报, 2007, 20(1): 85-90 ZHANG Qing-hua, LI Qiao, TANG Liang. Fracture Mechanism and Ultimate Carrying Capacity of Shear Connectors Applied for Steel concrete Joint Segment of Bridge Pylon[J]. China Journal of Highway and Transport, 2007, 20(1): 85-90 |
| [5] | 陈开利, 王戒躁, 安群慧. 舟山桃夭门大桥钢与混凝土结合段模型试验研究[J]. 土木工程学报, 2006, 39(3): 86-90 CHEN Kai-li, WANG Jie-zao, AN QUN-hui. Model Tests on Steel-concrete Joining Section of Main Girder of a Cable-stayed Bridge[J]. China Civil Engineering Journal, 2006, 39(3): 86-90 |
| [6] | 刘荣, 余俊林, 刘玉擎, 等. 鄂东长江大桥混合梁结合段受力分析[J]. 桥梁建设, 2010(3): 33-35 LIU Rong, YU Jun-lin, LIU Yu-qing, et al. Mechanical Analysis of Joint Sections of Hybrid Girder of Edong Changjiang River Bridge[J]. Bridge Construction, 2010(3): 33-35 |
| [7] | BOUAZAOUI L, PERRENOT G, DELMAS Y, et al. Experimental Study of Bonded Steel Concrete Composite Structures[J]. Journal of Constructional Steel Research, 2007, 63(9): 1268-1278 |
| [8] | VALENTE I B, CRUZ P J S. Experimental Analysis of Perfobond Shear Connection between steel and Lightweight Concrete[J]. Journal of Constructional Steel Research, 2004, 60(9): 465-479 |
| [9] | 黄彩萍, 张仲先, 陈开利. 混合梁斜拉桥钢-混结合段试验与传力机理研究[J]. 华中科技大学学报:自然科学版, 2012, 40(1): 67-71 HUANG Cai-ping, ZHANG Zhong-xian, CHEN Kai-li. Model Test and Transfer Mechanism of Steel-concrete Composite Structure for Hybrid Girder Cable-stayed Bridges[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2012, 40(1): 67-71 |
| [10] | 肖林, 李小珍, 卫星. PBL剪力键静载力学性能推出试验研究[J]. 中国铁道科学, 2010, 31(3): 15-21 XIAO Lin, LI Xiao-zhen, WEI Xing. Research on the Static Load Mechanical Properties of PBL Shear Connectors' Push-out Test[J]. China Railway Science, 2010, 31(3): 15-21 |
| [11] | JTG/T D64-01-2015, 公路钢混组合桥梁设计与施工规范[S]. JTG/T D64-01-2015, Specification for Design and Construction of Highway Steel-concrete Composite Bridge[S]. |
| [12] | 聂建国. 钢-混凝土组合结构桥梁[M]. 北京: 人民交通出版社, 2011. NIE Jian-guo. Steel-concrete Composite Bridges[M]. Beijing: China Communications Press, 2011. |
 2017, Vol. 34
2017, Vol. 34
