扩展功能
文章信息
- 苗晓燕, 陈昌富, 王思逸
- MIAO Xiao-yan, CHEN Chang-fu, WANG Si-yi
- 有限填土地震主动土压力计算上限法
- Upper-bound Method for Calculating Seismic Active Earth Pressure with Limited Backfill
- 公路交通科技, 2017, 34(3): 38-44
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(3): 38-44
- 10.3969/j.issn.1002-0268.2017.03.006
-
文章历史
- 收稿日期: 2016-04-25
有限填土挡土墙广泛存在于公路、铁路、房建、市政等工程中,传统的朗肯和库仑土压力理论不再适用[1]。为此,谢小荣[2]、高印立[3]基于土的塑性上限理论,研究了该类挡墙主动与被动土压力计算方法。马平[4]根据极限平衡理论及平面滑裂面假定,推导得到有限土体滑裂面剪切破坏角的数学表达式。但上述计算均假定墙土界面光滑,这与实际情况不符。为此,王洪亮[5]、李峰[6]考虑墙土界面摩擦影响,研究了紧邻既有建筑基础挡墙的土压力,但其假设墙背直立、墙后填土面水平。
上述研究成果[2-7]均假定填土为单滑块破坏模式。然而,应宏伟[8-9]通过有限元数值分析发现,随着墙后填土宽度的逐渐减小,土体将进一步形成双滑块甚至多滑块破坏模式。GRECO[10-11]也认为有限填土土体破坏为双滑块或多滑块破坏模式,并采用极限平衡法,分别研究了有无地震力作用下主动土压力的计算方法,但未考虑超载影响。
众所周知,除填土性质外,超载和地震作用对土压力的分布影响很大,因此,本文在前人[8-11]研究的基础上,按照有限土体滑裂面的发展形式,假定其破坏模式为单滑块和双滑块两种模式,基于Mononobe-Okabe拟静力法和塑性理论上限法,考虑墙背倾斜粗糙、墙后填土面和填土后岩层面倾斜,推导得到了在地震和超载共同作用下有限填土主动土压力上限解,最后与已有试验结果及现有计算方法进行对比分析,验证了本文方法合理、可行。
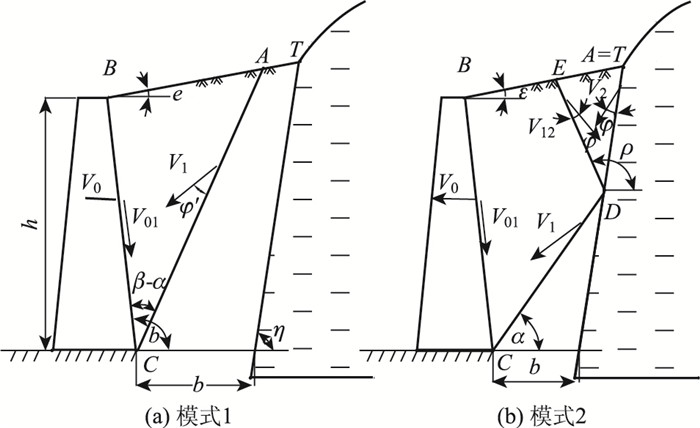
1 有限填土破坏模型及假定有限填土破坏模型如图 1所示,本文假定:(1) 墙后填土为无黏性土,满足摩尔-库仑破坏准则;(2) 按平面应变问题分析,墙体在土压力作用下产生平动;(3) 视有限填土宽度不同,墙后土体达到主动极限状态时形成一个或两个刚性滑动楔体,分别如图 1(a)与图 1(b)所示;(4) 作用在楔体上的地震力采用拟静力法计算,只考虑水平地震力作用,且水平地震系数为k。

|
| 图 1 破坏模型和滑动平面 Fig. 1 Failure modes and slip planes |
| |
设挡墙高h;墙后填土面坡角ε;填土内摩擦角和重度分别为φ′和γ;墙背水平倾角为β;墙背与墙土间摩擦角为δ;岩层面水平倾角为η;墙底填土宽度为b。
由图 1可知,当墙底填土宽度b较大时,与水平面夹角为α的滑裂面CA逸出填土表面 (A点位于BT之间),此为单滑块破坏模式,称为模式1。
当墙底填土宽度b较小时,与水平面夹角为α的第一滑裂面CD与岩面相交于D点,同时与水平面夹角为ρ的第二滑裂面DE与填土表面相交于E点,此为双滑块破坏模式,称为模式2。
显然,墙底填土宽度b的大小决定有限填土的破坏模式,因此,我们把由模式1转换到模式2的临界墙底填土宽度bc称为界限宽度。
2 粗糙墙主动土压力计算 2.1 模式1主动土压力S1计算分析对于δ=φ′的粗糙墙[12]情况。依相关联流动法则,土楔ABC下滑速度V1与滑动面AC成φ′角,相对于墙体平移速度V0的相对速度V01与滑动面BC成φ′角,其速度场见图 2(a)。根据速度相容原理,有:

|
| 图 2 模式1速度和作用力图 Fig. 2 Velocity and acting forces in Mode 1 |
| |
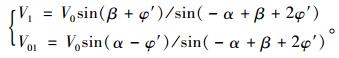
|
(1) |
如图 2(b)所示,土楔体ABC上的作用力有:楔体重力W1;水平地震力H1=kW1;主动土压力S1;填土表面超载Q。由于填土为无黏性土,滑面AC上不会因黏聚力而产生内能耗散。根据外功率与塑性变形区内部能量损耗率相等原理,有:

|
(2) |
解得:
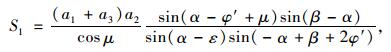
|
(3) |
式中参数为:
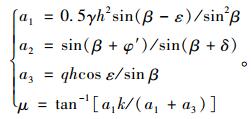
|
(4) |
由式 (3)、式 (4) 可见,主动土压力S1取决于角α。对角α求导得S1的极值点α=α1c,将α1c代回式 (3) 可得S1的极大值,即粗糙墙模式1最大主动土压力。具体过程如下:

|
(5) |
解得:

|
(6) |
式中参数为,
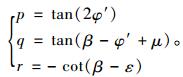
|
(7) |
设TC面与水平面夹角为αmin,由几何关系得:
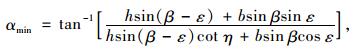
|
(8) |
显然,若
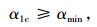
|
(9) |
则滑面逸出点A位于BT之间,模式1成立;否则,进入模式2。界限宽度bc可由式 (8)、式 (9) 解得:
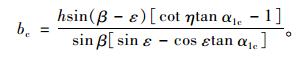
|
(10) |
模式2中,有限填土形成过墙踵C点的双折线破坏面CDE,楔体EDT沿TD面滑动,速度为V2;楔体BCDE沿CD面滑动,速度为V1。二者相对速度为V12。挡土墙水平移动速度为V0,楔体BCDE与挡土墙的相对速度为V01。其速度场见图 3(a)。依据速度相容原理,V2, V12可用V0表示如下:

|
| 图 3 模式2的速度和作用力图 Fig. 3 Velocity and acting forces in Mode 2 |
| |
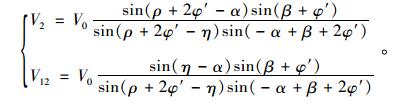
|
(11) |
图 3中ymax为T点到墙底平面的竖直距离,y为第一道破裂面与岩层交点D到墙底平面的竖直距离。ymax可表示为:
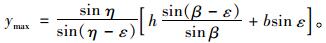
|
(12) |
楔体BCDE的作用外力有楔体重力W1,水平地震力H1=kW1,主动土压力S2,BE段填土表面超载Q1;而楔体EDT的作用外力有楔体重力W2,水平地震力H2=kW2,ET段填土表面超载Q2。
同样,根据外功率与塑性变形区内部能量损耗率相等,有:
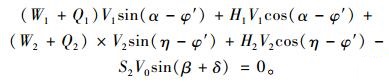
|
(13) |
将式 (11) 代入式 (13) 并简化得:
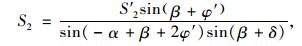
|
(14) |
式中,
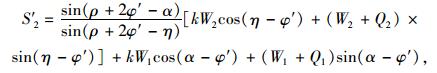
|
(15) |
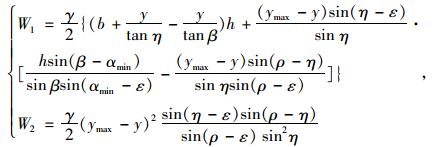
|
(16) |
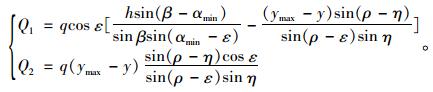
|
(17) |
由式 (14)~式 (17) 可见,主动土压力S2取决于角α和ρ,分别对α,ρ求导,求得S2极值点的α=α2c,ρ=ρ2c,将α2c,ρ2c代回式 (14) 可求S2的极大值即为粗糙墙模式2最大主动土压力,其计算过程如下:
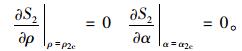
|
(18) |
由式 (18) 中的第一式求得:
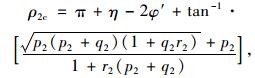
|
(19) |
式中参数为:
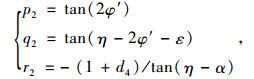
|
(20) |
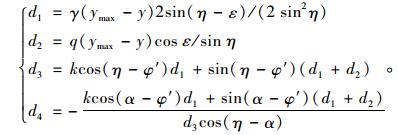
|
(21) |
由于α=tan-1[ysinη/(bsinη+ycosη)],故式 (18) 第二式等价于:
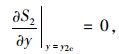
|
(22) |
求导后化简得到如下三次方程式 (23),求解得y2c,代回前式可求得α2c。
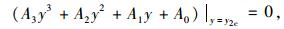
|
(23) |
式中参数为:
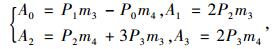
|
(24) |
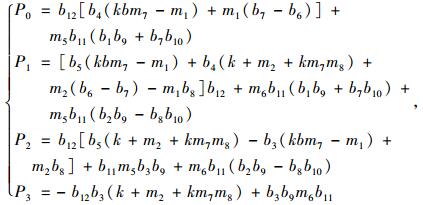
|
(25) |
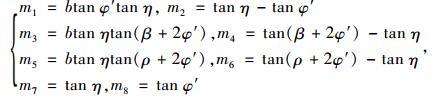
|
(26) |
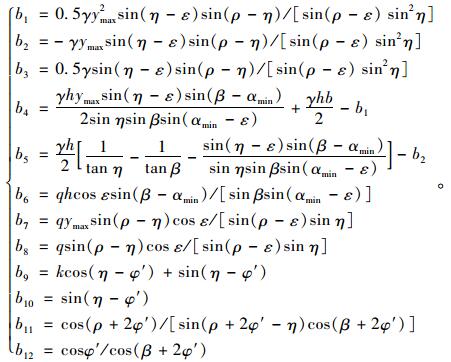
|
(27) |
对于δ=0的光滑墙[12]情况,模式1与模式2中假设速度场如图 4所示,与粗糙墙不同的是,此时挡土墙与楔体相对速度V01沿墙背BC向下,并与墙背平行。除此以外,模型假设与计算原理等均与粗糙墙情况相同,此处仅列出主动土压力计算公式和参数改变部分。
|
| 图 4 模式1和模式2的速度场 Fig. 4 Velocity fields in Mode 1 and Mode 2 |
| |
3.1 模式1主动土压力S1计算公式
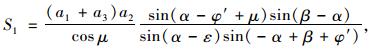
|
(28) |
式中参数同粗糙墙式 (4),仅第二式改为:
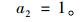
|
(29) |
α1c的计算公式同粗糙墙式 (6)~式 (7),仅式 (7) 第一式改为:
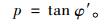
|
(30) |
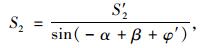
|
(31) |
式中S′2同粗糙墙式 (15)。
ρ2c的计算公式同粗糙墙式 (19)~式 (21)。
α2c的计算公式同粗糙墙式 (22)~式 (27),但是需将式 (26) 第三式和第四式分别改为:
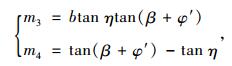
|
(32) |
另将式 (27) 最后两式分别改为:
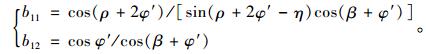
|
(33) |
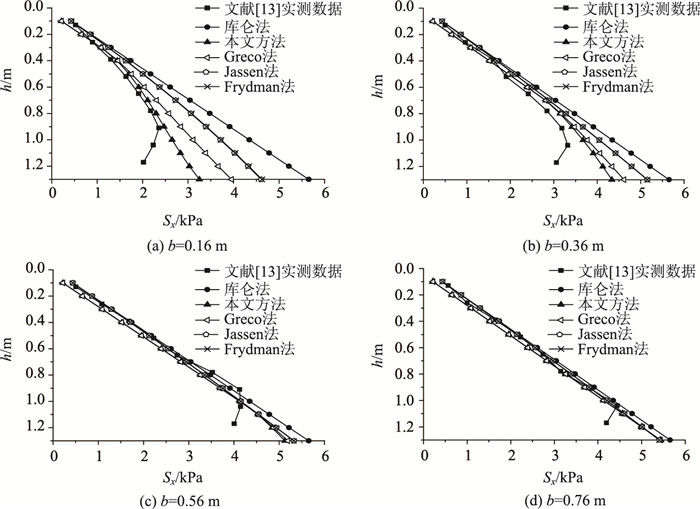
文献[13]针对墙后有限宽度无黏性土,开展了3种墙体变位模式下的主动土压力室内模型试验,通过观测墙后不同宽度土体的破坏过程和土压力大小,对有限填土的破坏模式及主动土压力分布规律进行了探讨。本文参照其刚性挡墙平动模式的试验数据,并与库仑法及Jassen法[14]、Frydman法[1]、Greco法[10]对比分析,以验证本文方法的合理性。文献[13]参数如下:ε=0°,γ=14.6 kN/m3,q=0,h=1.3 m,k=0,φ′=32.75°,b=0.16,0.36,0.56,0.76 m。考虑试验中装土箱侧壁涂抹了润滑油,取δ=0光滑墙情况分析。
本文方法中主动土压力不再随深度线性分布,难以直接对深度求导得到土压力强度的解析式。这里基于差分法表示主动土压力强度:
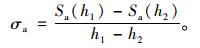
|
(34) |
本文方法和库仑法等得到的主动土压力计算结果以及文献[13]试验数据见图 5,由图 5可知:(1) 有限填土范围内,本文方法主动土压力值小于库仑法,呈非线性分布,σz随深度增加而增大,增大速率先快后慢。本文结果与Jassen法、Frydman法和Greco法趋势相似,且同试验数据最为吻合。(2) 随着b/h的增大,本文解逐渐增大向库仑解靠近,最终趋于一致,与主动土压力从有限填土模式过渡至半无限空间模式的过程相符。
|
| 图 5 有限填土下的主动土压力分布 Fig. 5 Distributions of active earth pressure under limited backfill |
| |
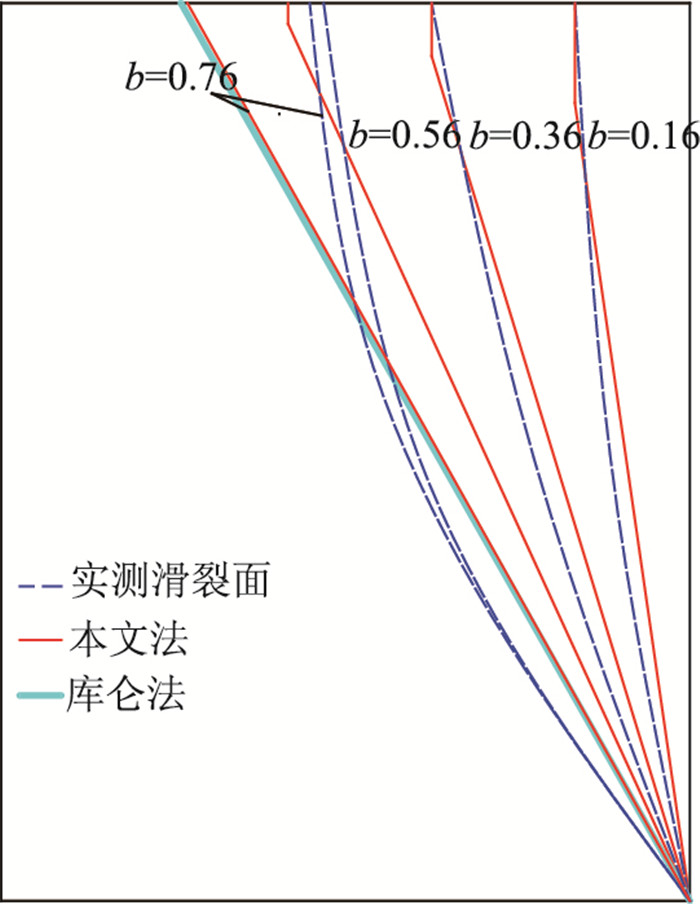
图 6为有限填土范围内库仑法与本文方法及实测滑裂面的对比。显然,库仑法破坏面与水平面的夹角始终为45°+φ′/2,与实测相差较大;而本文方法中滑裂面倾角α随b的增大而减小,当b增至界限宽度bc后保持恒定,与库仑滑裂面倾角重合,同实测破坏面吻合度较高。
|
| 图 6 有限填土下的滑裂面 Fig. 6 Slip surface under limited backfill |
| |
进一步分析表明:模式2较好地模拟了有限填土主动破坏形态,得到更加精确的主动土压力值;模式1则对应半无限空间体情况,是模式2的极限形式,从能量角度验证了库仑法。模式1和模式2的过渡点bc,是判断有限填土的界限宽度。
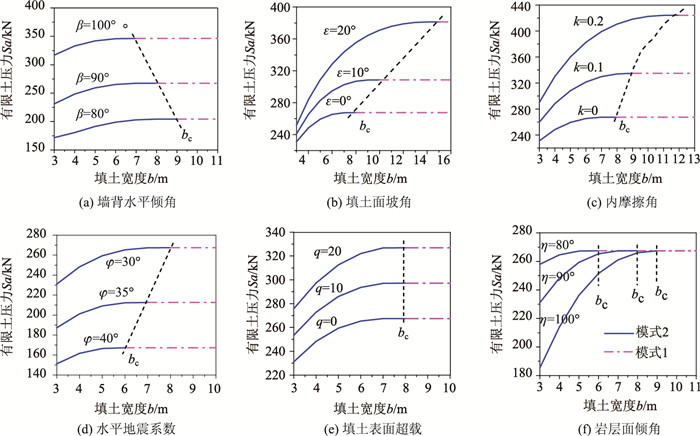
4.2 参数分析为探究有限填土各因素对挡墙主动土压力和填土破坏形态的影响,分别取墙背水平倾角β、填土面坡角ε、内摩擦角φ′、水平地震系数k、填土表面超载q、岩层面倾角η进行分析。设某挡墙h=10 m,η=β=90°,ε=0°,γ=18 kN/m3,q=0,k=0.2,δ=φ′=30°。各参数在此基础上分别变化,其对主动土压力和界限宽度的影响如图 7所示。由图 7可知:(1) 有限填土主动土压力随β,ε,k和q的增大而增大,随φ和η的增大而减小。其中,β和φ与半无限空间内影响相似,而ε,k,q的变化引起的差值小于半无限空间,η仅影响有限填土[15];(2) 界限宽度bc不恒定,β,φ增大bc变小,ε,k,η增大bc变大,而q对bc无影响。
|
| 图 7 有限填土各参数对主动土压力和界限宽度的影响 Fig. 7 Influence of different parameters on active earth pressure and the boundary width under limited backfill |
| |
本文方法中β,ε,φ,δ对滑裂面倾角的影响与库仑法相似,而k,q对滑裂面倾角的影响如表 1所示。由表 1可知有限填土滑裂面倾角非定值,而是随b的增加逐渐变小,最终等于库仑破坏角,且随q的增加小幅增大,随k的增加明显减小。
| k, q | 不同填土宽度 (m) 下滑裂面倾角/(°) | 库仑破坏 角/(°) |
||||
| 4 | 6 | 8 | 10 | 12 | ||
| k=0,q=0 | 58.4 | 56.0 | 54.3 | 54.3 | 54.3 | 54.3 |
| k=0,q=10 kN/m | 58.6 | 56.5 | 54.3 | 54.3 | 54.3 | |
| k=0,q=20 kN/m | 58.7 | 56.9 | 54.3 | 54.3 | 54.3 | |
| k=0.1,q=0 | 56.7 | 53.2 | 49.8 | 48.6 | 48.6 | |
| k=0.2,q=0 | 55.0 | 50.6 | 46.7 | 43.5 | 41.8 | |
5 结论
本文通过建立有限填土单、双滑块破坏模型,基于Mononobe-Okabe法和极限分析上限定理,考虑填土表面超载及水平地震效应共同作用,推导了主动极限状态下滑裂面倾角和主动土压力的上限解,并得到如下结论:
(1) 有限填土主动土压力,当墙底填土宽度b小于界限宽度bc时,小于传统库仑主动土压力解;当b≥bc时,则近似等于库仑解。
(2) 有限填土主动土压力强度呈现上部为直线、下部为曲线的非线性分布,且有限填土越狭窄,上部直线段越短。
(3) 填土表面超载q越大,则有限填土主动土压力和滑裂面倾角越大;而水平地震系数k越大,有限填土主动土压力越大,滑裂面倾角越小。
(4) 库仑土压力理论用于有限填土情况时偏保守,而采用本文方法更符合实际,且适用于受地震、超载作用,墙体倾斜粗糙、墙后填土面倾斜、有限填土后岩面倾斜的情况。
| [1] | FRYDMAN S, KEISSAR I. Earth Pressures on Retaining Walls Near Rock Faces[J]. Journal of Geotechnical Engineering, 1987, 113(6): 586-599 |
| [2] | 谢小荣, 张可能, 许宏武, 等. 极限分析法计算有限土体主动土侧压力[J]. 西部探矿工程, 2005, 17(9): 22-23 XIE Xiao-rong, ZHANG Ke-neng, XU Hong-wu, et al. Calculation of Lateral Active Earth Pressure for Limited Soils by Limit Analysis Method[J]. West-China Exploration Engineering, 2005, 17(9): 22-23 |
| [3] | 高印立. 极限分析法计算有限范围土体土压力[J]. 建筑结构, 2001, 17(8): 66-68 GAO Yin-li. Calculation of Finite Earth Pressure with Limit Analysis Method[J]. Building Structures, 2001, 17(8): 66-68 |
| [4] | 马平, 秦四清, 钱海涛. 有限土体主动土压力计算[J]. 岩石力学与工程学报, 2008, 27(增2): 3070-3074 MA Ping, QIN Si-qing, QIAN Hai-tao. Calculation of Active Earth Pressure for Limited Soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S1): 3070-3074 |
| [5] | 王洪亮, 宋二祥, 宋福渊. 紧邻既有建筑基坑有限土体主动土压力计算方法[J]. 工程力学, 2014, 31(4): 76-81 WANG Hong-liang, SONG Er-xiang, SONG Fu-yuan. Calculation of Active Earth Pressure for Limited Soil between Existing Building and Excavation[J]. Engineering Mechanics, 2014, 31(4): 76-81 |
| [6] | 李峰, 郭院成. 基坑工程有限土体主动土压力计算分析研究[J]. 建筑科学, 2008, 24(1): 15-18 LI Feng, GUO Yuan-cheng. Analytical Study on Active Soil Pressure from Finite Soil Body in Construction Pit[J]. Building Science, 2008, 24(1): 15-18 |
| [7] | 杨明辉, 汪罗成, 赵明华. 考虑土拱效应的双排抗滑桩桩侧土压力计算[J]. 公路交通科技, 2011, 28(10): 12-17,39 YANG Ming-hui, WANG Luo-cheng, ZHAO Ming-hua. Calculation of Soil Pressure against Double-row Anti-slide Piles Considering Soil Arching Effect[J]. Journal of Highway and Transportation Research and Development, 2011, 28(10): 12-17,39 |
| [8] | 应宏伟, 郑贝贝, 谢新宇. 狭窄基坑平动模式刚性挡墙被动土压力分析[J]. 岩土力学, 2011, 32(12): 3755-3762 YING Hong-wei, ZHENG Bei-bei, XIE Xin-yu. Study of Passive Earth Pressures against Translating Rigid Retaining Walls in Narrow Excavations[J]. Rock and Soil Mechanics, 2011, 32(12): 3755-3762 |
| [9] | 应宏伟, 黄东, 谢新宇. 考虑邻近地下室外墙侧压力影响的平动模式挡土增主动土压力研究[J]. 岩石力学与工程学报, 2011, 30(增2): 2970-2978 YING Hong-wei, HUANG Dong, XIE Xin-yu. Study of Active Earth Pressure on Retaining Wall Subjected to Translation Mode Considering Lateral Pressure on Adjacent Existing Basement Exterior Wall[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S1): 2970-2978 |
| [10] | GRECO V. Active Thrust on Retaining Walls of Narrow Backfill Width[J]. Computers and Geotechnics, 2013, 50: 66-78 |
| [11] | GRECO V. Analytical Solution of Seismic Pseudo-static Active Thrust Acting on Fascia Retaining Walls[J]. Soil Dynamics and Earthquake Engineering, 2014, 57(2): 25-36 |
| [12] | 陈惠发. 极限分析与土体塑性[M]. 北京: 人民交通出版社, 1995: 205. CHEN Hui-fa. Limit Analysis and Soil Plasticity[M]. Beijing: China Communications Press, 1995: 205. |
| [13] | 杨明辉, 戴夏斌, 赵明华, 等. 墙后有限宽度无粘性土主动土压力实验研究[J]. 岩土工程学报, 2016, 38(1): 131-137 YANG Ming-hui, DAI Xia-bin, ZHAO Ming-hua, et al. Experimental Study on Active Earth Pressure of Cohesionless Soil with Limited Width behind Retaining Wall[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(1): 131-137 |
| [14] | JANSSEN H A. Versuche uber Getreidedruck in Silozellen[J]. Zeitschrift des Vereines Deutscher Ingenieure, 1895, 35: 1045-1049 |
| [15] | 张孝彬, 乐金朝. 半填半挖路基挡土墙静止土压力计算[J]. 公路交通科技, 2014, 31(6): 17-22 ZHANG Xiao-bin, YUE Jin-chao. Calculation of Static Earth Pressure on Retaining Wall of Cut-and-fill Subgrade[J]. Journal of Highway and Transportation Research and Development, 2014, 31(6): 17-22 |
 2017, Vol. 34
2017, Vol. 34
