扩展功能
文章信息
- 张期树, 徐则民, 夏香波, 任喆
- ZHANG Qi-shu, XU Ze-min, XIA Xiang-bo, REN Zhe
- 差异化锚长组合支护方式对边坡稳定性影响的数值分析
- Numerical Analysis on Influence of Support Pattern of Variation Bolt Length Combination on Slope Stability
- 公路交通科技, 2017, 34(3): 26-37
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(3): 26-37
- 10.3969/j.issn.1002-0268.2017.03.005
-
文章历史
- 收稿日期: 2016-03-24
2. 长安大学 建筑工程学院, 陕西 西安 710061
2. School of Architectural Engineering, Chang'an University, Xi'an Shaanxi 710061, China
随着公路、铁路等交通设施的大量建设,边坡数量增加,边坡稳定性和加固问题更加突出,使得锚杆支护在边坡加固工程中得到了广泛应用[1]。此外,锚杆具有成本低、支护效果良好、施工方便等优点[2]。目前,工程上通常采用等长锚杆加固边坡,使设计结果过于保守,造成了不必要的浪费[3]。彭文祥等[4]研究了边坡的锚杆长度、垂直间距、锚杆倾角、布设位置、锚杆直径和砂浆厚度对边坡安全系数的影响;林杭[5-7]等分析了边坡的锚杆倾角、布设位置和布设形式对边坡稳定性的影响;何忠明[8]等采用数值计算方法,建立了节理边坡的计算模型,探讨了结构面厚度对于节理边坡稳定性的影响,以及锚杆长度、倾角、间距与边坡安全系数的关系; 朱宏伟[9]等分析了锚杆支护边坡动力响应规律及锚固参数影响。以上研究侧重于分析锚杆参数对边坡稳定性的影响,且锚杆布设方式单调,基本按全坡面等长布置,而关于锚杆组合布设形式研究考虑较少。林杭等探讨了长短相间锚杆布设形式[3]、单调变化土钉布置形式[10]以及锚杆对称分布形式[11]在边坡中的应用;何忠明[12]等研究表明二级边坡中采用先短后长相间布置与一级边坡采用短锚杆、二级边坡采用长锚杆这两种形式能较好地加固风化岩质边坡。但这些研究中所提到的组合方案并没有阐述其来源或布设依据。另外,对于建议加强边坡中下部锚杆这一结论在文中虽有提及而未能在组合方案中加以体现[3, 5],仅直接运用软件设计一些简单组合方案进行对比分析,而在边坡不同部位布锚的实际效果方面欠虑。因此,本文通过有限差分软件FLAC3D,采用cable单元模拟锚杆,利用强度折减法[13-15]计算边坡安全系数,将单层 (不同层位) 布锚效果运用至 (锚长、锚固角) 差异化组合布锚形式中,力求发挥锚杆的最大加固效能,以期为边坡加固实践提供一种经济化的设计思路。
1 FLAC3D锚固力学模型及材料单元特性锚杆支护体系通过以下3种方式进行加固:(1) 锚杆自身的轴向作用;(2) 浆-岩界面间剪切作用;(3) 浆体界面法向作用。因此,全长黏结型注浆锚杆简化为黏结-滑移模型[16](如图 1所示)。其主要力学行为由2部分构成:一是通过具有一定剪切刚度的弹簧来模拟界面的抗剪切作用;二是采用滑块来模拟界面的黏结作用,即锚杆在拉拔作用下的抵抗滑移的行为[17]。
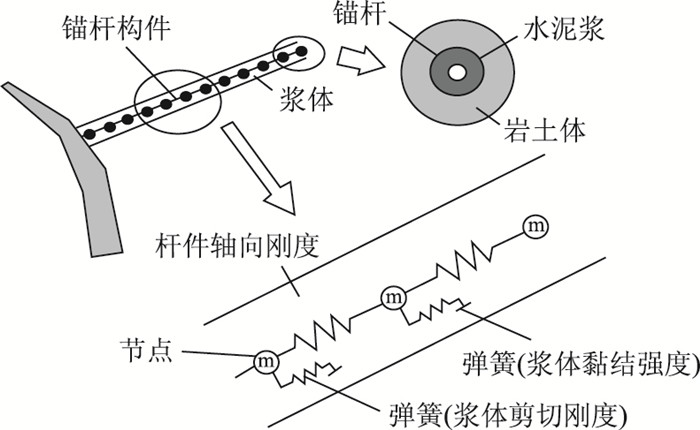
|
| 图 1 全长注浆加筋体力学模型 Fig. 1 Mechanical model of fully bonded reinforcement |
| |
单元轴向力学行为采用一维弹塑性本构模型描述[17](如图 2所示):
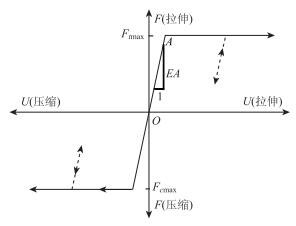
|
| 图 2 杆体材料力学特性 Fig. 2 Material behavior of bolt Cable |
| |
(1) 弹性OA段:轴向刚度
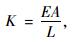
|
式中,A为锚单元横截面积;E为弹性模量;L为锚单元长度。
由轴向位移增量Δut计算轴向力增量ΔFt
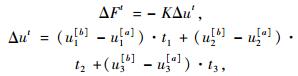
|
式中,ui[a],ui[b]为节点位移,i=1, 2, 3;[a], [b]分别为节点a, b;t1; t2, t3分别为锚单元轴向的方向余弦。
(2) A点以后,即cable单元轴力达屈服状态 (拉伸Ft max或压缩Fc max) 时,轴力不再增加,轴向刚度下降至0,单元可无限伸缩。
cable包括杆件部分和浆体部分,由里及外分别为杆件、浆体、岩土体。锚杆或锚索一般是多个cablese l (锚杆构件) 的集合,每个cablese l与2个node连接组成cable element,其局部坐标系如图 3所示,中心轴与x轴一致,x轴正向为node 1指向node 2。与周围岩土体的加固机制为当土体变形后,外荷载通过浆体作用在node上,node的变形又引起锚杆构件产生力学行为,结果为反向反作用于土体,最终实现力学平衡。浆体力学机理体现在锚杆与岩土体界面间的黏结-摩擦,故采用黏结-滑块模型描述其行为,锚-浆与浆-岩界面发生相对位移us时,通过浆体参数计算响应。杆单元element力学机制为杆内的受力变形通过节点node传递,杆单元仅为2个自由度,通过位移u1,u2呈现,且杆单元轴力与之对应,具体内容详见FLAC3D手册[18]。
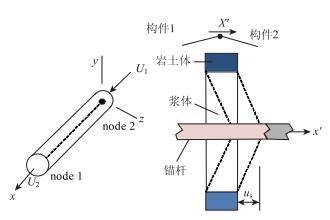
|
| 图 3 Cable单元局部坐标系及锚-岩界面相对位移 Fig. 3 Cable element local coordinate system and relative displacement at interface between anchorage and rock |
| |
2 计算模型
本文选用文献[3]中的边坡模型作为研究对象,边坡高20 m,坡角为59°。模型计算范围符合张鲁渝等[13]提出的最佳模型尺寸要求,长×高×厚=92 m×40 m×1 m,按平面应变问题分析[5]。模型尺寸与土体参数见图 1,锚杆参数如表 1所示。边界条件为底部固定,左右水平约束,上部自由。采用Mohr-Coulomb强度准则,初始应力场按自重考虑。计算收敛准则为最大不平衡力比率满足1×10-5的精度要求[18]。通过计算得到该边坡安全系数为0.96( < 1.0),说明边坡处于临界失稳状态,需采取一定的支护措施,故本文拟采用锚杆加固边坡。
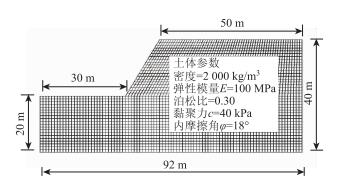
|
| 图 4 模型与土体参数 Fig. 4 Model and parameters of soil |
| |
| 弹性模量/ GPa |
锚杆直径/ mm |
黏结刚度/ (MN·m-2) |
砂浆黏结 力/kPa |
内摩擦角/ (°) |
锚孔直径/ mm |
| 200 | 30 | 10 | 35 | 25 | 100 |
3 单层布锚支护效果的差异分析 3.1 边坡层位确定
由均质土坡滑裂面为圆弧状特征可知,不同坡高处的滑动面迹线与坡面间的相对距离d差异明显,且滑动面迹线可用自编FISH程序提取并量化得到。如图 5所示,可见差异表现为:从坡脚剪出口至坡顶拉裂区范围内,d逐渐增大 (d3 < d2 < d1),且迹线向坡体内侧的延伸速率由快变缓。此外,坡面组成要素沿坡面向下依次为:坡肩、坡腰和坡脚。为研究在不同坡体部位 (简称边坡层位) 单独布锚对边坡稳定性的贡献,按上述差异对边坡分层,除坡顶垂直向下2 m为覆盖层外,剩余坡体按三要素将边坡大致分成:坡顶层、坡腰层和坡脚层。
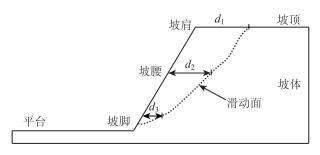
|
| 图 5 边坡要素及初始边坡滑动面位置 Fig. 5 Slope factors and initial slope sliding surface position |
| |
3.2 单层布设方案
在各层位单独布设3根相同长度、相同倾角的一组锚杆,布设形式:取锚长L范围为2~20 m (2 m递增),锚固角θ范围为[5°, 50°](5°递增),覆盖层以下18 m的竖向布锚间距为2 m,在坡顶层、坡腰层和坡脚层分别布设锚杆组,编号分别为1#~3#,4#~6#,7#~9#。具体布置如图 3所示 (以L=10 m,θ=25°为例说明)。

|
| 图 6 各层位布锚形式 Fig. 6 Forms of arranging bolts in each layer |
| |
3.3 结果分析
图 7为不同层上锚长与安全系数的结果关系曲线,可知在坡顶和坡腰层布设2~6 m短锚杆的加固效果甚微。其中存在一段曲线斜率较大的部分,表明边坡稳定性提升迅速。除坡脚层外,当锚固角较小时,坡顶与坡腰层的安全系数随锚长增加不断提高,且加固效果处于该层位的高水平。各关系曲线均存在一个“拐点”位置,当锚长超过拐点值后曲线基本趋于水平,说明此后继续增长锚杆对支护效果已无明显帮助,可知边坡锚固存在有效锚长Leff[5](锚固角小的Leff >20 m),且Leff在各层上出现的速率不一致,这跟坡面与滑动面迹线间的相对距离d有关。坡顶至坡脚层对应的安全系数域分别为[1.0, 1.19], [1.0, 1.35]和[1.0, 1.27],可见从整体上来说,加强坡体中、下部更利于边坡稳定,尤其在坡腰层布设长锚杆,这也符合边坡“固脚强腰”的防治思想[19-20]。此外,对比图 7(a)~(c)可知,采用短锚杆 (2~8 m) 加固坡脚层时,锚固效果立即凸显,关系曲线斜率大,安全系数增幅快且达“拐点”(Leff) 迅速。加之图 5中坡脚层处d3较短,锚杆能快速穿过滑动面并达有效锚长,故在坡脚层不宜布设长锚杆。
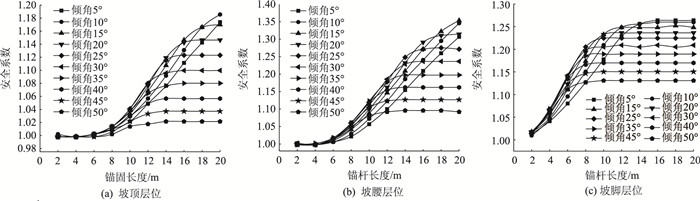
|
| 图 7 锚长与安全系数的关系 Fig. 7 Relationship between anchoring length and safety factor |
| |
图 8为锚固角与安全系数的关系曲线,可见除几组短锚杆之外,安全系数系数均随锚固角增大呈先上升后降低的趋势,峰值处即为最佳锚固角。还可知,在未达峰值之前,关系曲线斜率随锚长增加而增大,由此可知,锚杆越长,锚固效果提升速度越快;最佳锚固角位置随锚长增加而逐渐减小,二者大致呈负线性关系。
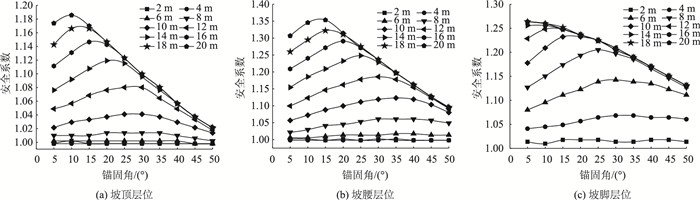
|
| 图 8 锚固角与安全系数的关系 Fig. 8 Relationship between anchoring angle and safety factor |
| |
图 9为锚长4,10 m和16 m在各层上的关系曲线,可知除坡顶和坡腰层的4 m锚长外,相同长度锚杆组布设在不同层位上所表现出的加固效果差异显著,从而验证了边坡层位的合理性以及下述分层差异化组合布锚研究的必要性。
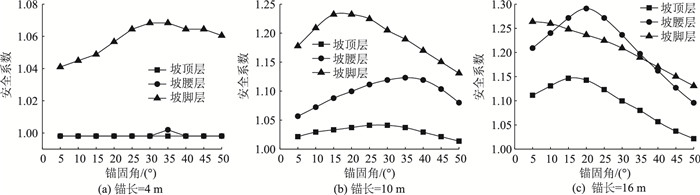
|
| 图 9 锚杆组在边坡各层位上的关系曲线 Fig. 9 Relation curves of bolt group in each layer of slope |
| |
4 差异化锚长组合方案 4.1 方案依据来源与分析思路
为便于研究锚长差异化 (即各层锚杆组锚长存在差别) 组合形式与边坡稳定性的关系,笔者按长度将锚杆分成:短锚杆 (2~6 m)、中长锚杆 (8~12 m)、长锚杆 (14~18 m)3类, 提出从坡顶至坡脚依次将锚杆组布设成:长-中-短型、中-长-短型、短-长-中型三大组合形式。其中,长-中-短型布设依据源于滑动面迹线与坡面间的相对距离d的大小 (对应d1>d2>d3);中-长-短型与短-长-中型布置方式,依据的原则是单层布锚结论中重点加强坡体中下部 (尤其坡腰层) 锚长更利于边坡稳定且在坡脚层不宜布设长锚杆,在中-长-短型的坡脚层选择布设短锚杆,在短-长-中型的坡脚层选择布设中长锚杆。以下研究内容的分析思路为:通过限定边坡锚杆总使用量90 m[3],设竖向间距为2 m,全坡面布3组,共9根锚杆,锚固角θ∈[5°,50°](5°递增),按坡顶、坡腰、坡脚层顺序依次固定所在层锚长,然后调整余下两层位间的相对锚长作为对比方案。受篇幅所限,以下9组方案用不同方式进行穿插分析,未能一一详述。另外,将各层锚杆组的锚固角按上述单层最佳锚固角 (在下述各图中横坐标为 (*) 处) 作为附加方案加入对比分析 (则每种组合有11种锚固角布设工况),由此分析各层锚杆组锚长变化对安全系数的敏感度SL以及锚固角变化对锚固效果及滑动面的影响规律。
4.2 “长-中-短”型布锚形式如图 10所示。
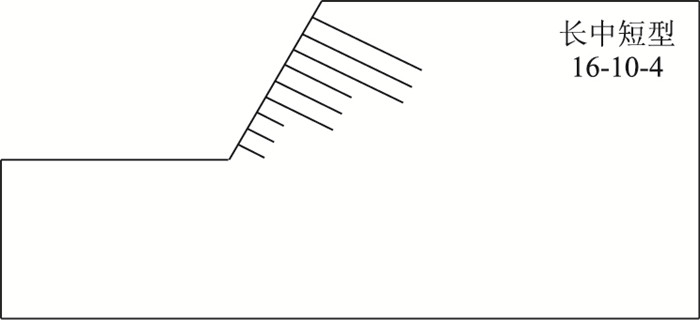
|
| 图 10 长中短型布设形式 Fig. 10 long-medium-short layout |
| |
(1) 固定坡顶层-长锚杆组
坡顶层锚长固定为16 m,然后调整坡腰与坡脚层间的相对锚长,组合形式有:16-8-6(以下简称A1;单位:m),16-10-4(A2),16-12-2(A3) 共3种,所得安全系数变化曲线见图 11,可知3个组合的安全系数均随锚固角增大呈先升后降的趋势,大致呈拱形分布,且最佳锚固角θopt均在30°左右。以下对锚固角θ予以分段讨论。当θ < 23°时,安全系数在同一锚固角下的大小为A1>A3>A2,彼此差异较小,说明三者锚固效果基本相当,且当坡脚或坡腰层锚杆组达该层锚杆长度类型的最大值时,锚固效果更优;当进一步比较A1与A3时,发现坡脚层布置最长短锚杆将最具优势,故A1最优,A3次之,而A2中坡腰与坡脚层的锚杆组均处于中等长度 (无优势锚长),则安全系数相较最低。当θ∈[23°, 36°]时,安全系数大小为A3>A1>A2,可见A3中坡腰层的中长锚杆对安全系数大小起重要作用,A1中坡脚层的最长短锚杆作用次之,而A2仍因坡腰与坡脚层的锚长未集中突出,安全系数最低。当θ>36°时,安全系数优势从坡腰层的中长锚杆逐渐转移至坡脚层的短锚杆。具体为:θ∈[36°, 43°]属安全系数优势因素的过渡段;θ∈[43°, 50°]时,安全系数优势则完全过渡至坡脚层短锚杆,且短锚杆越长优势越明显。
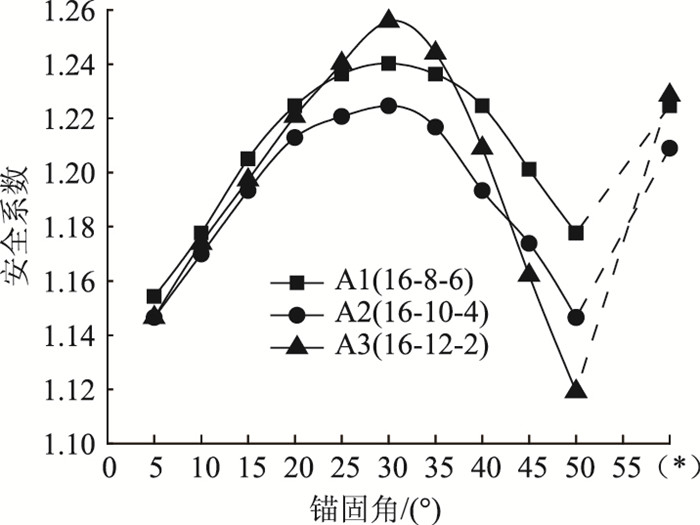
|
| 图 11 固定坡顶层锚长方案 Fig. 11 Scheme of bolt length for fixing slope top layer 注:(*) 处A1-A3的锚固角组合依次为:15°-35°-30°,15°-35°-32.5°,15°-30°-20° |
| |
(2) 固定坡腰层-中长锚杆组
固定坡腰层锚长为10 m,然后变化坡顶与坡脚两层间的相对锚长,组合形式有:18-10-2(B1),16-10-4(B2),14-10-6(B3),结果见图 9,可知3个组合的最佳锚固角θopt位置差异较大,B1-B3分别为20°,30°和40°。当θ < 27°并忽略坡腰层的影响时,可知坡顶层锚长对安全系数差异起主控作用,表现为坡顶锚杆越长,安全系数越高。这是由于长锚杆在坡体中的端部随锚长增加逐渐深入坡体内侧,而端部又决定了滑动面位置,故滑动面趋近于坡体内侧,约束浅层滑动,滑动体增大,相应地边坡失稳将需要提供更大的致滑力。因此,按小锚角布设时宜增长坡顶层长锚杆。θ∈[27°, 33°]为安全系数差异的过渡域。当θ>33°时,相同锚固角下,安全系数差异的主控因素转至坡脚层短锚杆,短锚杆越长,坡脚层的布锚区范围越大,亦即土体强度提高的区域扩大,则安全系数越高。因此,采用大锚角布设时,宜加长坡脚层短锚杆。(注:图 12横坐标 (*) 处B1-B3的锚固角组合依次为:12.5°-35°-20°,15°-35°-32.5°,20°-35°-30°)
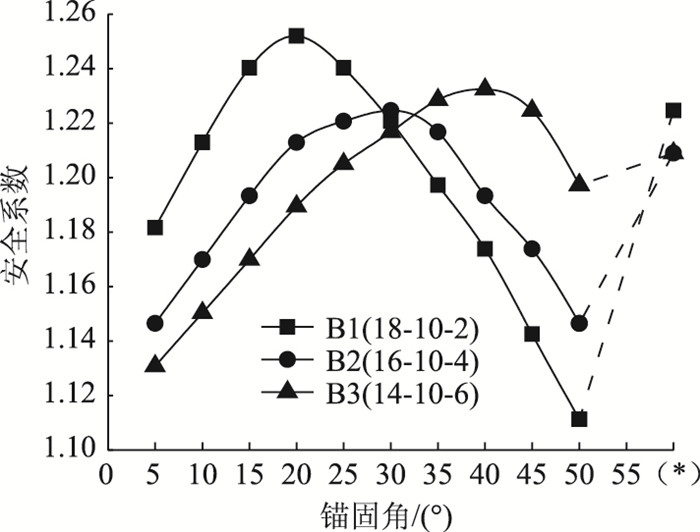
|
| 图 12 固定坡腰层锚长方案 Fig. 12 Scheme of bolt length for fixing slope waist layer |
| |
(3) 固定坡脚层-短锚杆组
将坡脚锚长设为定值4 m,然后调整坡顶与坡腰间的相对锚长,具体组合有:18-8-4(C1),16-10-4(C2),14-12-4(C3)。结果曲线见图 13,可知C1-C2的最佳锚固角θopt分别为16°,30°,36°。当θ < 21°时,C1-C3间安全系数差异主要由坡顶层锚杆引起,坡顶层锚杆越长,支护效果越佳,且在此范围内三者安全系数均随锚固角增加而增大。因此,当坡脚层锚长固定时,宜加长坡顶层长锚杆,相应地缩短坡腰层锚杆 (即扩大两层间的锚长差,以提高锚固效果)。同样,θ∈[21°, 31°]为安全系数差异控制因素过渡段;当θ∈[31°, 50°]时,坡腰层中长锚杆端部随锚固角增大逐渐转向坡体下侧、近坡面靠近,而其对滑动面位置起支配作用。故安全系数随锚固角增大持续降低,出现该现象的原因为坡顶层所布长锚杆已穿过滑动面一定距离并达有效锚长,且C1-C3在坡脚层所布锚长相同,则安全系数差异主要由坡腰层锚杆组引起。因此,可能在某一锚固角下,边坡破坏模式由深层滑动突变成浅层滑动,安全系数由此开始降低。
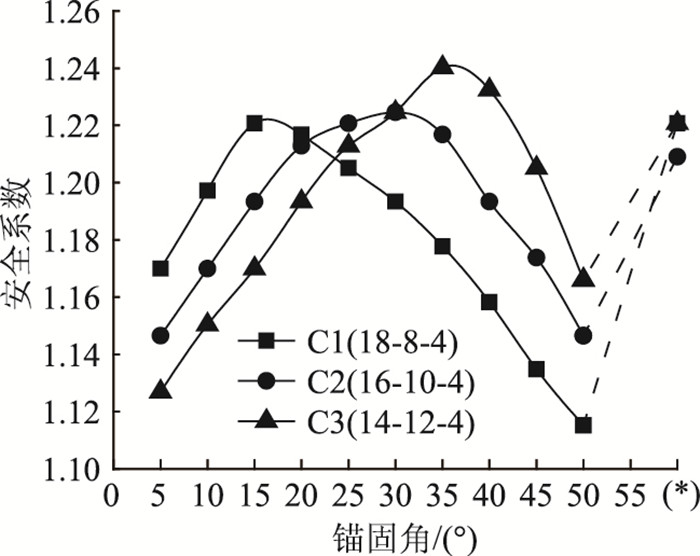
|
| 图 13 固定坡脚层锚长方案 Fig. 13 Scheme of bolt length for fixing slope foot layer 注:(*) 处C1-C3锚固角组合依次为:20°-30°-32.5°,15°-35°-32.5°,12.5°-35°-32.5° |
| |
综上所述,长中短型的最大安全系数为1.252,比原始边坡仅提高了约25%。以过渡段作为分界位置,之前锚固角范围称为小锚角段,后段范围为大锚角段。该型组合的优化结论见表 2。
| 固定 层位 |
锚固角类型 | |
| 小锚角 | 大锚角 | |
| 坡顶 | 宜集中增长坡腰层或坡脚层锚长 | 宜突出坡脚层锚长 |
| 坡腰 | 宜增长坡顶层锚长,缩短坡脚层锚长 | 宜突出坡脚层锚长 |
| 坡脚 | 宜增长坡顶层锚长,缩短坡腰层锚长 | 宜突出坡腰层锚长 |
4.3 “短-长-中”型
布锚形式如图 14所示。
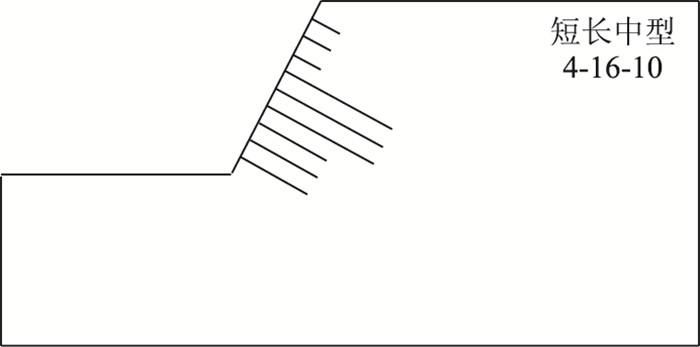
|
| 图 14 短长中型布设形式 Fig. 14 Short-long-medium layout type |
| |
(1) 固定坡顶层-短锚杆组
固定坡顶层锚长为4 m,然后调整坡腰与坡脚层间的锚长,具体组合有:4-14-12(D1),4-16-10(D2),4-18-8(D3)。结果见图 15,最佳锚固角θopt分别为30°,35°,35°,安全系数域为[1.24,1.44],比原始边坡提高了24%~44%,较长中短型支护水平高出近1倍。当θ < 32°时,安全系数大小为D3>D1>D2,在相同锚固角下,D3与D1间的安全系数差值明显大于D1与D2,说明加强坡腰层比坡脚层的效果突出,而D2各层上锚长均不集中突出,故安全系数最低。θ∈[32°,35°]为过渡段。当θ>35°时,三者安全系数差异甚小,但仍以坡脚层锚长突出为佳。
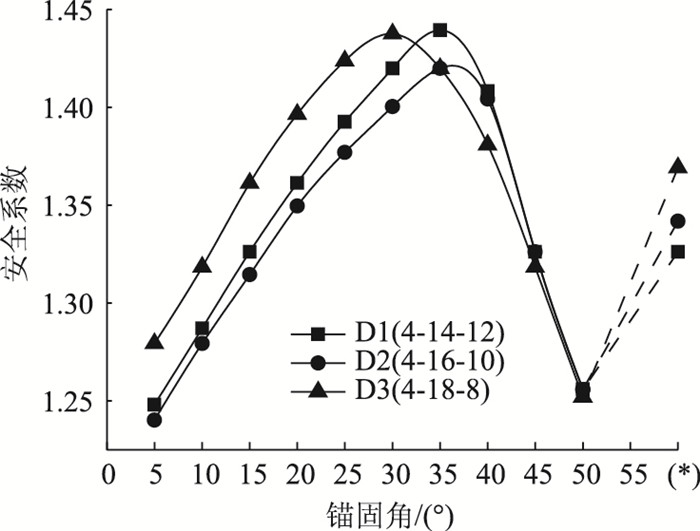
|
| 图 15 固定坡顶层锚长方案 Fig. 15 Scheme of bolt length for fixing slope top layer 注:(*) 处D1-D3锚固角组合依次为:20°-25°-12.5°,20°-20°-17.5°,20°-15°-25° |
| |
此结论还可据各层锚杆组轴力占边坡锚杆总轴力的百分比来加以印证,结果如图 16所示,可见坡顶层锚杆所占比重小;当θ < 35°时,坡腰层锚杆轴力比例均随锚固角增大而增加,且每增长2 m,比例上升约15%~20%,说明坡腰层锚杆越长,轴力所占比重越大,其发挥程度越高,而相对应地坡脚层锚杆在缩短 (锚长差),比例不断下降。
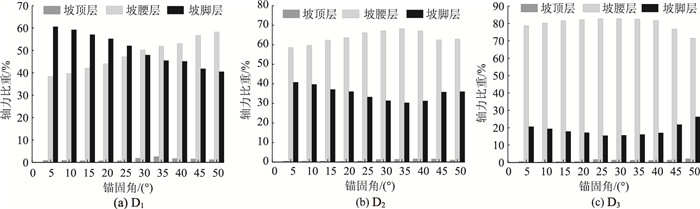
|
| 图 16 D1-D3在不同锚固角下的各层轴力比重 Fig. 16 Proportion of bolt axial force for D1-D3 in each layer |
| |
对于D1,坡腰与坡脚层间所布锚长差异小,当两层间锚杆轴力比重彼此较为接近时达最佳锚固状态;而对于D2和D3,在最佳锚固角下时,坡腰与坡脚层间比重出现最大差值,说明最佳锚固状态与坡腰层锚杆轴力最高程度地发挥几乎同步。轴力比重在坡腰层大小依次为D3>D2>D1,在坡脚层为D1>D2>D3,可知D2在这两层位上的轴力发挥程度均一般,都不具备突出优势,故安全系数最低。当θ>35°时,安全系数大小为D1>D2>D3,但之间三者差异随锚固角增大逐渐变小,而综合对比图 13可得,在相同锚固角下,坡脚层轴力水平大小为D1>D2>D3,说明此时以突出坡脚层锚长为佳。
另外,对D2的总轴力与安全系数数据进行一元线性回归分析[21],记总轴力为Xi,安全系数为Yi,数据见表 3,得到回归直线方程为y=0.02x+1.07,且线性回归显著,由此可知,锚杆总轴力值越大,边坡的锚固效果越好[12]。
| 锚固角/(°) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 总轴力/MN | 8.037 | 8.971 | 10.336 | 11.782 | 13.712 | 15.126 | 15.946 | 15.366 | 11.981 | 10.645 |
| 安全系数 | 1.24 | 1.279 | 1.314 | 1.35 | 1.377 | 1.4 | 1.42 | 1.404 | 1.326 | 1.256 |
(2) 固定坡腰层-长锚杆组
组合形式有:2 -16-12(E1),4-16-10(E2),6-16-8(E3)。从轴力比重、坡顶层单独布锚结论可知,布置在坡顶层的短锚杆对边坡的加固作用微弱,且3种组合在坡腰层所布锚长均相同,则此时考虑坡脚层锚长变化对加固作用的影响即可。由图 17可知,在整个锚固角范围内不存在过渡段,当θ < 45°时,安全系数大小为E1>E2>E3,由此说明坡脚层中长锚杆越长,边坡越稳定。当θ>45°时,由于坡腰与坡脚层的锚杆均已达到有效锚长以及坡顶层短锚杆对加固作用影响较小,图中3条关系曲线几乎重合,说明3种组合的支护效果基本相当。因此,当固定坡腰层锚长时,可适当地缩短坡顶层锚杆,相应地增长坡脚层锚杆为宜。
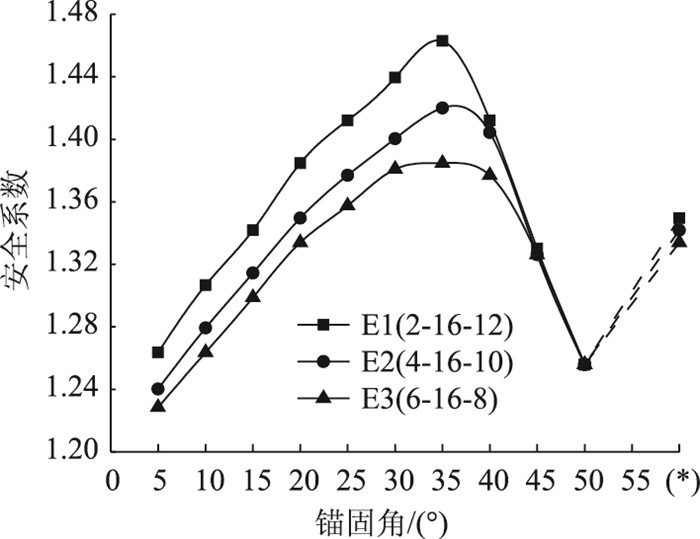
|
| 图 17 固定坡腰层锚长方案 Fig. 17 Scheme of bolt length for fixing slope waist layer 注:(*)处E1-E3锚固角组合依次为: 20°-20°-12.5°,20°-20°-17.5°,20°-20°-25° |
| |
(3) 固定坡脚层-中长锚杆组
组合方式有:6-14-10(F1),4-16-10(F2),2-18-10(F3)。关系曲线见图 18,可知当θ < 38°时,安全系数大小为F3>F2>F1,在忽略坡脚层锚杆组影响后,坡腰层的锚长变化将主导安全系数差异。换言之,坡顶与坡腰间的锚长差越大,安全系数越高,则此时宜突出坡腰层锚长,且F3组合在θ=33°时安全系数达峰值1.48,加固效果十分显著。图中过渡段并不明显。当θ>41°时,F1~F3间安全系数基本相同,这与坡脚层所布锚长相同有关。
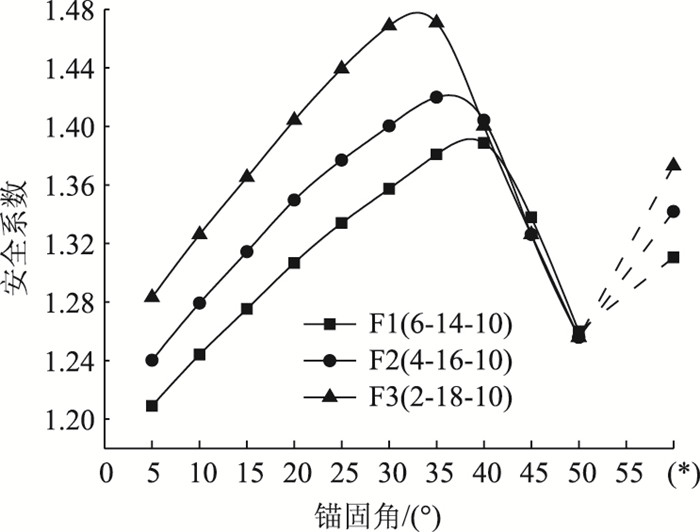
|
| 图 18 固定坡脚层锚长方案 Fig. 18 Scheme of bolt length for fixing slope foot layer 注:(*)处F1~F3锚固角组合依次为20°-25°-17.5°,20°-20°-17.5°,20°-15°-17.5° |
| |
通过轴力比重分析短长中型加固效果,可知轴力比重规律与安全系数差异特征匹配。除D类方案中存在过渡段之外,其他两大组合方案中无明显过渡段。采用小锚角布设时,宜适当加长坡腰层长锚杆,这点与单层布锚结论相符;而采用大锚角时,坡顶层短锚杆加固作用甚微, 且坡腰与坡脚层锚杆均已达有效锚长,故支护效果趋同。
4.4 中-长-短型布锚形式如图 19所示。
|
| 图 19 中长短型布设形式 Fig. 19 Medium-long-short layout type |
| |
(1) 固定坡顶层-中长锚杆组
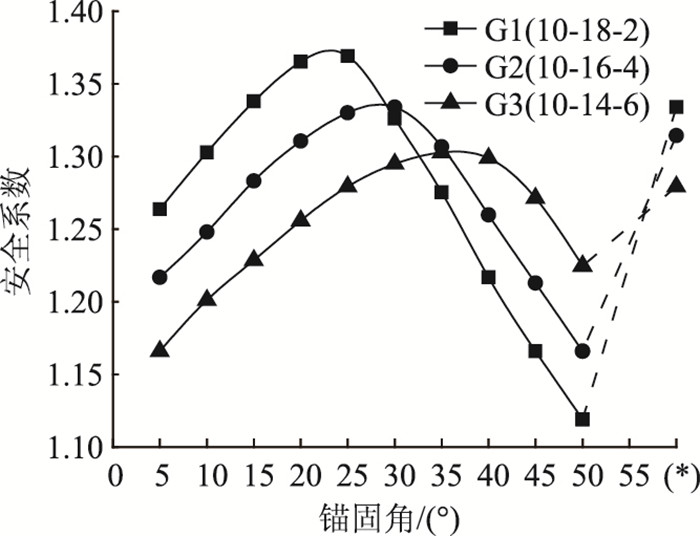
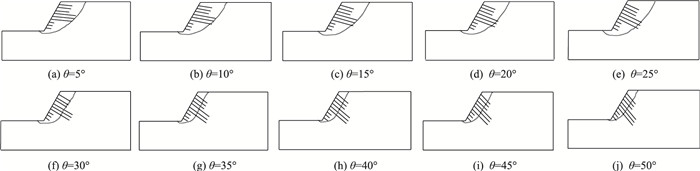
具体组合有:10-18-2(G1),10-16-4(G2),10-14-6(G3)。关系曲线见图 20,可知当θ < 29°时,在相同锚固角下,坡腰与坡脚层间锚长差越大,安全系数越高;θ∈[29°,36°]为过渡段;当θ>36°时,安全系数差异由坡脚层短锚杆体现,且锚杆越长,安全系数越高。限于篇幅,仅以G2为例阐明边坡滑动面迹线及其随锚固角变化时受控于锚杆组的变化规律,通过FLAC3D自编FISH语言搜索出边坡最大剪应变数据量化得到滑动面迹线,如图 21所示,对θ∈[5°, 50°],以过渡段为分界位置进行分段讨论。当按小锚角布设时,滑动面主要受控于坡腰层长锚杆端部,并随锚固角增大,坡体内锚杆端部均向坡体下方、内侧移动;同时,边坡上缘拉裂区逐渐远离坡肩,剪出口穿出坡脚左侧平台,并与坡脚的距离逐渐拉大,边坡破坏模式逐渐发展为深层滑动。因此,小锚角范围对应为滑动面变缓、滑体变大、后移的过程。当锚固角正好介于过渡段范围内时,坡腰层长锚杆已穿过滑动面一定距离,滑动面位置转由坡顶层中长锚杆的端部控制;一旦锚固角大于过渡段时,边坡破坏模式立刻由深层滑动突变为浅层滑动,滑动面将受控于坡脚层短锚杆。这是由于锚杆打入土体后形成筋土复合体,当其范围扩展至极限后,若滑动面继续向坡体内侧发展时,则对应的安全系数或所需滑动能量均比临坡面附近的大,从而迫使滑动面转向近坡面位置,变成浅层滑动破坏,具体表现为剪出口由坡脚左侧平台突变至坡脚上方坡面,坡顶拉裂区突变至坡肩后方附近,而此时坡顶与坡腰层锚杆均已穿出滑动面,仅坡脚层短锚杆端部贴近于滑动面。因此,在大锚角情况下,滑动面形状由坡脚层短锚杆主控。G1、G3滑动面受控于锚杆组的顺序与G2类似,仅各层锚杆组控制锚固角范围大小不同而已。所以,在G类方案中,随锚固角增加,滑动面迹线所受锚杆组控制的先后顺序为:坡腰层长锚杆-坡顶层中长锚杆-坡脚层短锚杆。
|
| 图 20 固定坡顶层锚长方案 Fig. 20 Scheme of bolt length for fixing slope top 注:(*) 处G1-G3锚固角组合依次为:27.5°-15°-20°,27.5°-20°-32.5°,27.5°-25°-30° |
| |
|
| 图 21 锚杆组与滑动面的位置关系 Fig. 21 Positional relations between bolt group and sliding surface |
| |
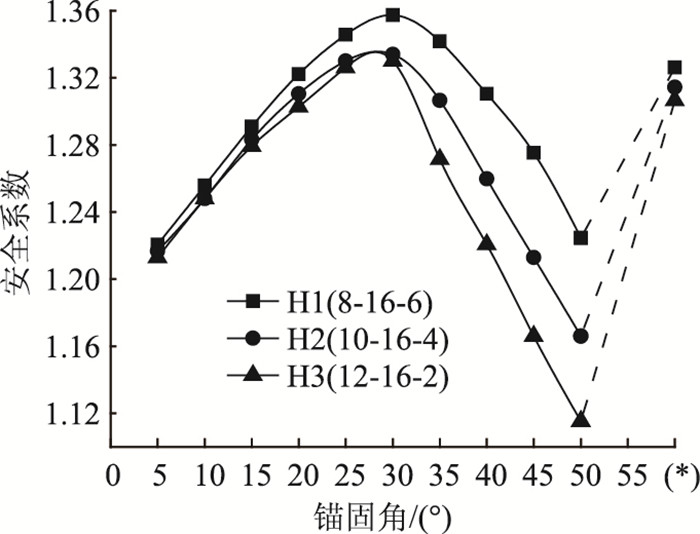
(2) 固定坡腰层-长锚杆组
具体组合有:8-16-6(H1),10-16-4(H2),12-16-2(H3)。结果如图 22所示,H类组合的最佳锚固角θopt均在30°左右,整个θ范围内无过渡段,安全系数大小始终保持为H1>H2>H3。当θ < 30°时,三者安全系数差异较小 (尤其H2与H3)。这是因为边坡稳定基本都由坡腰层长锚杆控制 (轴力比重也可阐明,此处不再赘述),而安全系数差异由坡脚与坡顶层间的锚长差产生。当θ>30°时,H1-H3间的安全系数差异随锚固角增加而扩大,而此时坡顶层锚杆组已作用不大,仅与坡脚层短锚杆锚长有关,即短锚杆越长,安全系数越高。
|
| 图 22 固定坡腰层锚长方案 Fig. 22 Scheme of bolt length for fixing slope waist layer |
| |
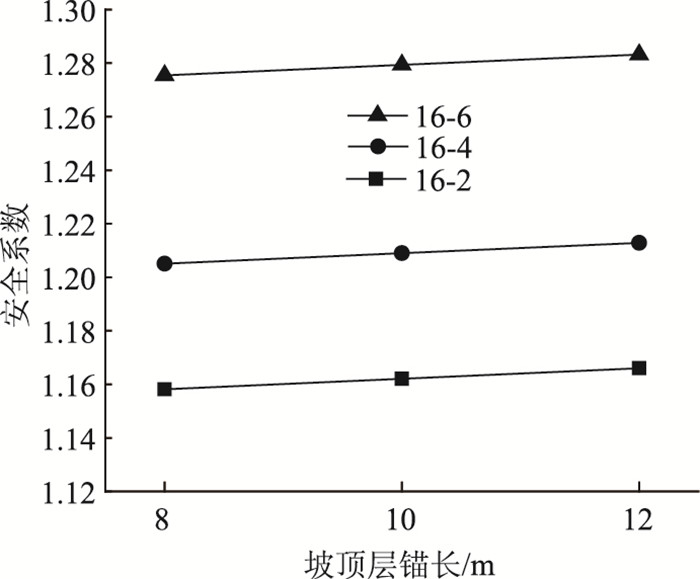
为进一步验证上述θ>30°时所得结论的正确性,通过布设大锚角 (以θ=45°为例) 分析坡顶层中长锚杆的锚长变化对安全系数的灵敏度SL。先固定G1-G3中坡腰与坡脚层锚长,然后改变坡顶层锚长分别为8,10 m和12 m,结果见图 23。从横向观察可知,3条曲线增幅均较小 (Δmax < 0.004);而从纵向观察,当固定坡顶与坡腰层锚长,仅改变坡脚层短锚杆的长度时 (分别固定图中横坐标8,10 m和12 m,然后观察对应y值),可以清晰地看出三者间安全系数差值 (Δmin>0.04)。因此,改变坡脚层锚长比改变坡顶层锚长所得的安全系数变化幅度大一个数量级,而此时坡腰层对应的长锚杆已穿出滑动面并达有效锚长Leff,对安全系数差异已无明显影响。因此,按大锚角布设时,安全系数差异的主控因素为坡脚层短锚杆。
|
| 图 23 坡顶层锚长与安全系数的关系 Fig. 23 Relationship between bolt length of slope top and safety factor |
| |
(3) 固定坡脚层-短锚杆组
具体组合有:8-18-4(I1),10-16-4(I2) 和12-14-4(I3)。结果如图 24所示,可见当θ < 28°时,安全系数大小为I1>I2>I3,说明安全系数与坡腰锚长正相关,与坡顶锚长负相关,增长坡腰锚杆组有利于支护;θ∈[28°,36°]为过渡段;当θ>36°时,坡脚层短锚杆控制滑动面位置,坡顶与坡腰层间的锚长差产生了安全系数差异;当θ∈[40°,50°]时,3种组合间的安全系数差异是由坡顶层锚长控制,而I2与I3的关系曲线基本重合,故笔者判定此时坡顶10 m锚长已达有效锚长Leff。为验证该观点的正确性,变化坡顶锚长分别为10,12 m和14 m,选择锚固角40°,45°和50°,计算结果如表 4所示,可知在同一锚固角下,增加坡顶锚长安全系数不变,说明坡顶层10 m锚长≥有效锚长Leff,那么进一步增长坡顶层锚杆无异于浪费材料,增加成本。
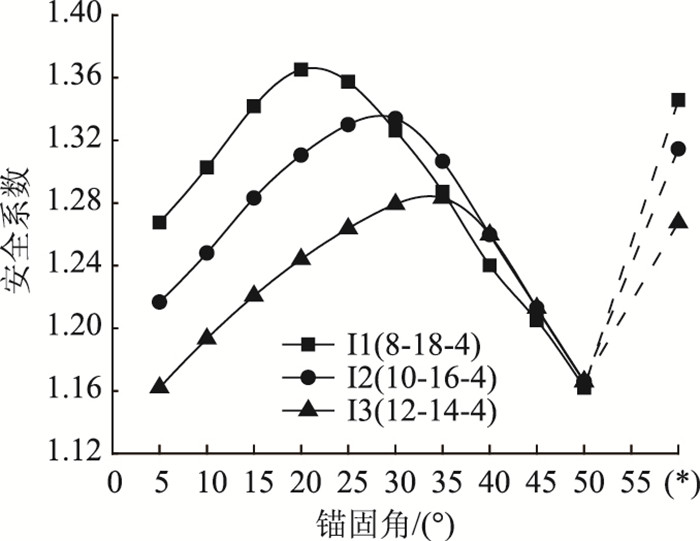
|
| 图 24 固定坡脚层锚长方案 Fig. 24 Scheme of bolt length for fixing slope foot layer 注:(*) 处I1-I3锚固角组合依次为27.5°-15°-32.5°,27.5°-20°-32.5°,27.5°-25°-32.5° |
| |
| θ/(°) | Lbolt | ||
| 10 m | 12 m | 14 m | |
| 40 | 1.259 765 625 | 1.259 765 625 | 1.259 765 625 |
| 45 | 1.208 984 375 | 1.208 984 375 | 1.208 984 375 |
| 50 | 1.166 015 625 | 1.166 015 625 | 1.166 015 625 |
综上,按小锚角布设时,宜增长坡腰层锚杆;按大锚角布设时,宜突出坡脚层锚长。此外,利用锚杆端部与滑动面的相对位置, 描述中-长-短型组合布锚时滑动面在整个锚固角内受锚杆组控制的规律为:坡腰长锚杆-坡顶中长锚杆-坡脚短锚杆;还通过分析边坡稳定性对层位锚长变化的灵敏度SL来判定主控因素,进一步佐证了有关结论的正确性。
4.5 组合-群锚效应与最优锚固角组合形式当各层锚杆组的锚固角θ按单层布锚所得的最佳锚固角进行布设 (如I3组合按27.5°(θtop)-25°(θwaist)-32.5° (θfoot) 布设,3层锚杆组的θ皆不相同) 时,且从上述各组合关系曲线图可知,除C1曲线外,其余组合横坐标 (*) 的安全系数与曲线峰值相比,仅达中等或中等偏上水平。究其主因在于:相邻层间锚杆组的锚固角存在差别 (如I3的坡顶层27.5°,坡腰层25°,Δθ=-2.5° < 0),使相邻层间锚杆间距逐渐缩小 (如I3组合中第3根与第4根间间距 < 2 m),打破了锚杆的正常布设间距2 m,导致各层锚杆组在锚固角组合情况下出现了“组合-群锚效应”(本质为群锚效应,出现该现象是由于相邻层锚固角“组合”(Δθ < 0) 时造成锚杆间距缩小,而Δθ>0时,加固效果趋好),即锚杆在彼此交界层域内产生了应力场重叠,影响了单根锚杆承载力的发挥,进而减小了锚杆的抗拔力并增加位移量[5],故弱化了支护效果。
为得到组合布锚下的最优锚固角组合形式,经大量合理试算,发现各组合以整体最佳锚固角θopt为基准,再找到并固定此锚固角下的主控层锚杆组,而其他相邻层Δθ按5°~10°与之岔开 (以上层θ减小,以下层θ增加,目的是使相邻层间的Δθ>0) 布设才能达到更佳的加固效能 (安全系数:θ岔开组合≥整体最佳锚固角θopt)。最优锚固角组合要根据锚长组合下对应的整体最佳锚固角θopt进行具体优化选择 (主要为Δθ取值),本质是适当地扩大相邻锚杆组间的布设间距 (如C1组合中横坐标 (*):20°-30°-32.5°,Δθ1=10°>0,Δθ2=2.5°>0)。下面以4 m短锚杆、10 m中长锚杆和16 m长锚杆为例进行锚固角的组合优化,部分优化结果如表 5所示。
| 组合形式 | θtop/(°) | θwaist/(°) | θfoot/(°) | 安全系数 |
| 长中短型 16-10-4(30°) 1.224 609 375 |
25 | 30 | 35 | 1.228 515 625 |
| 20 | 30 | 40 | 1.220 703 125 | |
| 25 | 30 | 30 | 1.228 515 625 | |
| 30 | 30 | 35 | 1.224 609 375 | |
| 短长中型 4-16-10(35°) 1.419 921 875 |
30 | 35 | 40 | 1.419 921 875 |
| 35 | 35 | 40 | 1.423 828 125 | |
| 30 | 35 | 35 | 1.419 921 875 | |
| 中长短型 10-16-4(30°) 1.333 984 375 |
25 | 30 | 35 | 1.337 890 625 |
| 20 | 30 | 40 | 1.333 984 375 | |
| 25 | 30 | 30 | 1.337 890 625 | |
| 30 | 30 | 35 | 1.337 890 625 | |
| 30 | 30 | 40 | 1.337 890 625 | |
| 注:() 内为整体最佳锚固角θopt;下方为安全系数 | ||||
5 结论
(1) 各组合条件下安全系数均随锚固角呈拱形分布,即存在整体最佳锚固角θopt,大致介于20°~40°之间,集中于30°附近。与此同时,边坡层位上也存在有效锚长Leff。三大组合的整体锚固效果依次为:短长中型>中长短型>长中短型。
(2) 边坡滑动面和安全系数差异与锚杆组的布设层位、锚长以及锚固角θ均紧密相关,三大组合的滑动面主控层位锚杆组随锚固角θ增大的转移规律大致为:长中短型, 坡顶-坡腰-坡脚;短长中型, 坡腰与坡脚协同-坡顶;中长短型, 坡腰-坡顶-坡脚。层间锚长差引起安全系数差异。以过渡段为分界,差异化锚长组合的一般优化规律为:小锚固角宜突出坡腰层,大锚角宜重视坡脚层,这与单层布锚、固脚强腰结论匹配。
(3) 边坡各层锚固角当按单层布锚所得的最佳锚固角组合布设时,存在“组合-群锚效应”。各层锚杆组间的锚固角应适当地选择岔开进行组合,本质为增大锚杆组间的布设间距。
在实际工程中建议合理化采用差异 (锚长、锚固角) 组合布锚这一经济布置思路。
| [1] | 言志信, 刘灿, 彭宁波, 等. 交通荷载作用下锚固公路边坡动力响应[J]. 长安大学学报:自然科学版, 2015, 30(1): 62-67 YAN Zhi-xin, LIU Can, PENG Ning-bo, et al. Dynamic Response of Anchoring Highway Slope under Dynamic Loads[J]. Journal of Chang'an University:Natural Science Edition, 2015, 30(1): 62-67 |
| [2] | 陈尤, 韦秉旭, 唐辉湘. 基于FLAC~(3D) 的岩质边坡锚杆优化设计[J]. 中外公路, 2011, 31(6): 85-89 CHEN You, WEI Bing-xu, TANG Hui-xiang. Optimal Design of Bolt of Rock Slope Based on FLAC~(3D)[J]. Journal of China & Foreign Highway, 2011, 31(6): 85-89 |
| [3] | 林杭, 陈宝成, 范祥, 等. 锚杆长短相间布置形式对边坡稳定性的影响[J]. 中南大学学报:自然科学版, 2015, 46(2): 625-630 LIN Hang, CHEN Bao-cheng, FAN Xiang, et al. Effect of Bolt with Long-short Layout on Slope Stability[J]. Journal of Central South University:Science and Technology Edition, 2015, 46(2): 625-630 |
| [4] | 彭文祥, 赵明华, 袁海平, 等. 基于拉格朗日差分法的全长注浆锚杆支护参数优化[J]. 中南大学学报:自然科学版, 2006, 37(5): 1002-1007 PENG Wen-xiang, ZHAO Ming-hua, YUAN Hai-ping, et al. Parameters Analysis of Grouted Bolts by Lagrangian Difference Method[J]. Journal of Central South University:Science and Technology Edition, 2006, 37(5): 1002-1007 |
| [5] | 林杭, 曹平. 锚杆长度对边坡稳定性影响的数值分析[J]. 岩土工程学报, 2009, 31(3): 470-474 LIN Hang, CAO Ping. Numerical Analysis for Effect of Bolt Length on Stability of Slopes[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(3): 470-474 |
| [6] | 林杭, 曹平, 李江腾. 全长注浆锚杆布设方式对边坡稳定性的影响分析[J]. 解放军理工大学学报:自然科学版, 2010, 11(2): 137-141 LIN Hang, CAO Ping, LI Jiang-teng. Effect of Wholly Grouted Cable Layout Mode on Stability of Slope[J]. Journal of PLA University of Science and Technology:Natural Science Edition, 2010, 11(2): 137-141 |
| [7] | 林杭, 钟文文, 熊威, 等. 锚杆长度与边坡坡率对最优锚固角的影响[J]. 岩土工程学报, 2014, 36(增2): 7-11 LIN Hang, ZHONG Wen-wen, XIONG Wei, et al. Effect of Bolt Length And Slope Rate on Optimum Anchorage Angle[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(S2): 7-11 |
| [8] | 何忠明, 林杭. 节理岩体边坡稳定性的锚杆支护影响分析[J]. 公路交通科技, 2010, 27(11): 8-9 HE Zhong-ming, LIN Hang. Influence of Bolt Reinforcement on Stability of Rock Jointed Slope[J]. Journal of Highway & Transportation Research & Development, 2010, 27(11): 8-9 |
| [9] | 朱宏伟, 项琴. 锚杆支护边坡动力响应规律及锚固参数影响[J]. 公路交通科技, 2011, 28(7): 30-18 ZHU Hong-wei, XIANG Qin. Dynamic Response of Anchored Slopes and Influence of Anchoring Parameters[J]. Journal of Highway & Transportation Research & Development, 2011, 28(7): 30-18 |
| [10] | 林杭, 陈宝成, 钟文文. 单调变化土钉布置形式对边坡稳定性的影响[J]. 公路, 2014(6): 41-45 LIN Hang, CHEN Bao-cheng, ZHONG Wen-wen. Effect of Monotonous Variation of Nail Layout on the Slope Stability[J]. Highway, 2014(6): 41-45 |
| [11] | 林杭, 陈宝成, 钟文文. 锚杆对称分布形式对边坡稳定性影响分析[J]. 铁道建筑, 2014(8): 62-65 LIN Hang, CHEN Bao-cheng, ZHONG Wen-wen. Effect of Bolt with Symmetrical Layout on Slope Stability[J]. Railway Engineering, 2014(8): 62-65 |
| [12] | 何忠明, 蔡军, 胡庆国, 等. 支护参数对锚固风化岩质边坡稳定性影响的数值分析[J]. 长沙理工大学学报:自然科学版, 2014, 11(1): 48-52 HE Zhong-ming, CAI Jun, HU Qing-guo, et al. Numerical Analysis of Support Parameters on the Weathered Rock Slope Stability[J]. Journal of Changsha University of Science and Technology:Natural Science Edition, 2014, 11(1): 48-52 |
| [13] | SONG Hong-wei, DUAN Yan-yan, JIANG Jing, et al. Numerical Simulation on Bolted Rock Joint Shearing Performance[J]. Mining Science & Technology, 2010, 20(3): 460-465 |
| [14] | 赵尚毅, 郑颖人, 邓卫东. 用有限元强度折减法进行节理岩质边坡稳定性分析[J]. 岩石力学与工程学报, 2003, 22(2): 254-260 ZHAO Shang-yi, ZHENG Ying-ren, DENG Wei-dong. Stability Analysis on Jointed Rock Slope by Strength Reduction FEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 254-260 |
| [15] | 张鲁渝, 郑颖人, 赵尚毅, 等. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]. 水利学报, 2003, 34(1): 21-27 ZHANG Lu-yu, ZHENG Ying-ren, ZHAO Shang-yi, et al. The Feasibility Study of Strength-reduction Method with FEM for Calculating Safety Factors of Soil Slope Stability[J]. Journal of Hydraulic Engineering, 2003, 34(1): 21-27 |
| [16] | 丁万涛, 刘金慧, 张乐文. 不同锈蚀度时海底隧道锚固支护结构岩锚相互作用分析[J]. 中南大学学报:自然科学版, 2014, 45(5): 1642-1652 DING Wan-tao, LIU Jin-hui, ZHANG Le-wen, et al. Analysis on Interaction of Rock-bolts in Anchorage Support Structure of Subsea Tunnel at Different Corrosion Levels[J]. Journal of Central South University:Science and Technology Edition, 2014, 45(5): 1642-1652 |
| [17] | 江文武, 徐国元, 马长年. FLAC_3D的锚杆拉拔数值模拟试验[J]. 哈尔滨工业大学学报, 2009, 41(10): 129-133 JIANG Wen-wu, XU Guo-yuan, MA Chang-nian. Numerical Simulation on Pull-tests of a Cable by FLAC_3D[J]. Journal of Harbin Institute of Technology, 2009, 41(10): 129-133 |
| [18] | Itasca Consulting Group Inc. Theory and Background[M]. Minnesota: Itasca Consulting Group, 2002. |
| [19] | 邹祖银, 陶连金, 朱占元, 等. 梅城公路K93+946~K94+082段边坡稳定性分析与加固研究[J]. 水文地质工程地质, 2009, 36(6): 89-93 ZOU Zu-yin, TAO Lian-jin, ZHU Zhan-yuan, et al. Stability Analysis and Reinforcement Study for the K93+946~K94+082 Section of the Slope of Meicheng Highway[J]. Hydrogeology & Engineering Geology, 2009, 36(6): 89-93 |
| [20] | 方薇, 杨果林, 刘晓红, 等. 非均质边坡稳定性极限分析上限法[J]. 中国铁道科学, 2010, 31(6): 14-20 FANG Wei, YANG Guo-lin, LIU Xiao-hong, et al. The Upper-Bound Limit Analysis of the Inhomogeneous Slope Stability[J]. China Railway Science, 2010, 31(6): 14-20 |
| [21] | 汪荣鑫. 数理统计[M]. 西安: 西安交通大学, 1986. WAN Rong-xin. Mathematical Statistics[M]. Xi'an: Xi'an Jiaotong University Press, 1986. |
 2017, Vol. 34
2017, Vol. 34
