扩展功能
文章信息
- 贾亮, 贺世开, 朱彦鹏, 郭健
- JIA Liang, HE Shi-kai, ZHU Yan-peng, GUO Jian
- 高填方路堤工后沉降监测试验研究
- Experimental Study on Monitoring of Post-construction Settlement of High-filled Embankment
- 公路交通科技, 2017, 34(3): 15-19, 25
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(3): 15-19, 25
- 10.3969/j.issn.1002-0268.2017.03.003
-
文章历史
- 收稿日期: 2016-05-19
路基是道路结构的基础,路基的稳定和变形控制是确保汽车快速、安全、舒适运行的前提。对高填方路堤,不仅要求施工中的安全可靠和竣工运营后的稳定,而且需要严格控制工后沉降,否则会出现局部路段的沉降过大,导致路基路面病害的发生。
国内学者从现场监测、试验研究、沉降预测方面开展了高填方路基沉降的研究。冯忠居等[1]依托某高填方路堤工程,现场测试了原地表沉降量、分层沉降量和地表水平位移。景宏君等[2]采用离心模型试验,研究了黄土高路堤沉降沿其高度、路线纵向和横断面方向的变化规律。黄涛等[3]对强夯结合碾压控制高填方沉降机理进行了试验分析。匡希龙等[4]提出用龚帕斯曲线法预测高填方路基的工后沉降。景宏君等[5]提出高路堤工后最终沉降量可采用灰色预测模型反映不均匀沉降趋势。王瑞甫等[6]提出了基于改进D-P弹塑性的地基模型沉降计算理论。肖衡林等[7]以实测沉降数据为基础,得出时间模型与泊松模型能较好地模拟沉降实测数据的结论。王丽琴等[8]提出了预测黄土路堤工后沉降的新模型。郑建国等[9]提出了适用于黄土路基沉降预测的方法。刘奉银等[10]采用层重固结法、层重未固结法得出黄土高填方路堤最终沉降计算方法。孙笑等[11]得到了典型断面高填方沉降变形规律。刘赪炜等[12]提出了一种适用于工程应用的半数值半解析方法。李华等[13]模拟了不同压实度对高填方路基沉降的影响。吴国雄等[14]分析了V形冲沟特有地形条件对超高路堤变形的影响。吕庆等[15-16]对高填方路堤工后沉降做出了预测。
在兰州至永靖沿黄河一级公路高填方路基桩号K24+400~405段布置单点沉降计,对高填方路堤沉降进行长期监测,并对兰永一级公路路堤施工中的稳定性分析及通车运营期的安全性分析提供基础数据。
1 工程及地质条件 1.1 地质条件本试验段主要为残坡积地层,成份为黏性土及卵砾石,地层分布有:(1) 黄土:厚度7.2~13.6 m,浅黄色,土质较均匀,干燥~稍湿,含砂量较高,主要以粉粒组成,可塑, Ⅱ级自重湿陷黄土。(2) 黄土:厚度4.5~5.1 m,浅红色,稍湿,土质较均匀,含砂量较高,黏粒含量高,硬塑。(3) 卵石:厚度2~4.6 m,黄褐色~青灰色,分选性差,磨圆度较好,骨架成份以变质砂岩碎屑组成,粒径2~10 cm,含量约占50%,最大粒径可见20 cm,细砂及少量土充填。(4) 泥岩:未见底,紫红色,中厚层状构造,泥质结构,成岩性好,泥质和钙质胶结,岩芯断面新鲜,软硬不均匀,暴晒易龟裂,岩芯呈短柱状。各层土体物理力学性质见表 1。
| 层号 | 土层名称 | 层厚/m | 含水率/% | 重度/(kN·m-3) | 孔隙比 | 压缩系数/ MPa-1 |
压缩模量/ MPa |
标贯击数 | 承载力特 征值/kPa |
| 1 | 黄土 | 10.4 | 8.5 | 14.1 | 0.96 | 0.21 | 6.2 | 7 | 150 |
| 2 | 黄土 | 4.8 | 16.5 | 14.9 | 0.89 | 0.23 | 7.6 | 8 | 180 |
| 3 | 卵石 | 3.3 | 21 | 24.8 | 1.15 | - | - | 19 | 400 |
| 4 | 泥岩 | 未见底 | - | 25.3 | - | - | - | >50 | 600 |
1.2 工程条件
兰永一级公路桩号K24+160~K25+838属于填方路基,选择在最高填方桩号K24+400~405段布置沉降监测设施。该段路堤最大填高18.3 m,路基右侧为陡峻山坡,左侧为泄洪河沟,路基横断面为半填半挖路基。工程设计中按照挖方土体就近利用原则,开挖的土方用作填方,不足填土就近利用恐龙湾隧道开挖的卵砾石材料。从原地面到路堤顶面具体填料为:原地面~12.3 m为黄土,12.3~16.1 m为砂卵石,16.1 m~路基顶面为卵砾石。
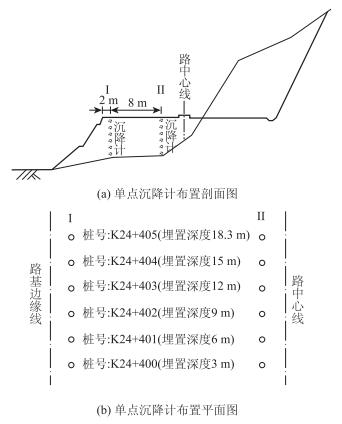
2 数据采集及试验设备现场埋设情况 2.1 试验设备及现场埋设情况沉降设备采用单点沉降计。单点沉降计具有对土质要求低、外界干扰少、可手动也可自动采集等优点。项目主要测试设备及型号为:沉降计用量程200 mm智能型JMDL-4720A、全密封标配机箱16点JMBV-1116综合采集模块、16通道JMZX-16ADTU手机上CMNET传输网模块、DSC测试系统软件JMZX-2007-1。用单点沉降计分别在左幅路基行车道和左路肩处沿道路纵向不同深度布置两列监测点,具体沉降计布置如图 1所示,编号和埋置深度如表 2所示。
|
| 图 1 单点沉降计布置示意图 Fig. 1 Layout of single-point settlement meters |
| |
| 单点沉降计编号 | 路肩 | 622730 | 622704 | 622751 | 622742 | 622764 | 622762 |
| 行车道 | 622724 | 622674 | 622680 | 622736 | 622723 | 622701 | |
| 埋置深度/m | 3 | 6 | 9 | 12 | 15 | 18 | |
2.2 试验数据采集
由于施工场地所限,沉降数据采集线临时设在路堤表层土体中,大约每月到现场1次挖出数据线手动采集数据。中央分隔带位置放线确定后,在中央分隔带位置安放自动采集设备,通过CMNET无线传输网自动采集数据,对路堤的沉降及稳定性作长期观测,获取第一手可靠资料,为我省以后公路建设中高填方路堤沉降研究提供基础数据。
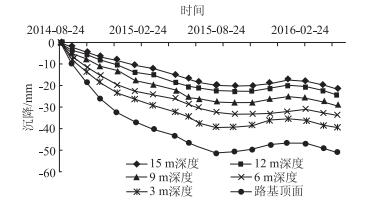
3 试验结果与分析 3.1 试验结果埋设沉降计后,2014年8月24日至2015年6月30日,约每月到现场手动采集数据1次。2015年6月30日安装自动采集设备后,用自动采集系统采集数据。路肩位置分层沉降与时间的关系如图 2所示,行车道位置分层沉降与时间的关系如图 3所示。
|
| 图 2 路肩分层沉降与时间的关系 Fig. 2 Relationship between settlement at depth under shoulder position and time |
| |
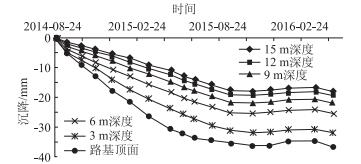
|
| 图 3 行车道分层沉降与时间的关系 Fig. 3 Relationship between settlement at depth under driveway position and time |
| |
由图 2、图 3可知,路肩位置沉降大于行车道位置沉降。路肩位置表面沉降相对较大,且一直呈现较大的增长趋势,其他位置沉降增加速度较慢。路基施工结束1 a后沉降基本趋于稳定。2015年10月1日道路通车后,路基在车辆荷载作用下沉降没有出现较明显的增大趋势。道路竣工后第1年12月到次年2月中旬,路堤不但没有出现沉降现象,反而出现了抬升,最大升高值出现在路肩位置的顶面,2月中旬升高达到峰值3 mm,2月中旬路堤开始沉降,4月中旬以后路堤沉降趋于稳定。高填方路堤沉降监测19个月后,得到路肩位置顶面最大沉降量51.02 mm,行车道位置顶面最大沉降量36.71 mm。
3.2 结果分析(1) 布置沉降监测设施的道路断面为半填半挖路基,且填方地面横坡较陡,受原地形影响,填方路基会发生水平位移。由图 1可知,路肩比行车道位置填方路基的水平位移大,较大的水平位移导致路基出现较大的竖向沉降[17-8];同时路肩的填方厚度大于行车道,较大填土厚度工后沉降较大,因而路肩位置的沉降大于行车道位置的沉降。
(2) 兰永线是兰州市区到永靖县 (刘家峡) 的旅游线路,通行车辆以小型汽车为主,基本没有重型车辆,荷载相对较小。通车后车辆荷载对高填方路堤沉降的影响很小,路基的分层沉降没有出现明显的增大趋势。
(3) 2015年12月至次年2月中旬,路堤不但没有出现沉降现象,反而出现缓慢升高现象,主要是由于兰永线位于季节性冻土地区,路堤出现了冻胀导致轻微的抬升。虽然路面结构设计中要进行防冻厚度验算,但从沉降实测数据发现路堤出现了轻微的冻胀。
4 沉降理论分析结果与实测结果比较 4.1 沉降理论分析模型高填方路基沉降理论模型主要有指数模型、双曲线模型、3点法幂函数模型、平方根模型、对数模型及《建筑地基基础设计规范》分层综合模型等[9, 16]。大量实践证明,规范法采用的系数偏大,故计算值均大于实测值[10]。根据现场实际结果,采用指数模型、双曲线模型、3点法幂函数模型、平方根模型及对数模型进行数据拟合预测最终路基的沉降量,进行预测值与实测值的对比。
4.2 理论结果与实测结果对比取路肩和行车道监测点工后沉降观测数据进行回归分析,以最终 (2016年5月5日) 沉降量为例对比理论结果与实测结果,如表 3、表 4所示。
| 深度/m | 实测值/mm | 对数模型 | 指数模型 | 幂函数模型 | 平方根模型 | 双曲线模型 | |||||||||
| 预测值/mm | 误差/% | 预测值/mm | 误差/% | 预测值/mm | 误差/% | 预测值/mm | 误差/% | 预测值/mm | 误差/% | ||||||
| 15 | -21.74 | -22.66 | 4.23 | -22.16 | 1.93 | -23.56 | 8.37 | -20.96 | -3.59 | -22.09 | 1.61 | ||||
| 12 | -24.25 | -24.86 | 2.51 | -24.28 | 0.12 | -25.47 | 5.03 | -22.55 | -7.01 | -25.62 | 5.65 | ||||
| 9 | -29.53 | -30.61 | 3.66 | -29.13 | -1.35 | -31.65 | 7.18 | -31.71 | 7.38 | -28.13 | -4.74 | ||||
| 6 | -34.02 | -34.45 | 1.26 | -34.58 | 1.65 | -34.97 | 2.79 | -37.38 | 9.88 | -35.93 | 5.61 | ||||
| 3 | -39.60 | -40.83 | 3.10 | -39.92 | 0.81 | -37.39 | -5.58 | -40.11 | 1.29 | -42.07 | 6.24 | ||||
| 0 | -51.02 | -50.66 | -0.71 | -52.06 | 2.04 | -54.79 | 7.39 | -48.17 | -5.59 | -52.31 | 2.53 | ||||
| 深度/m | 实测值/mm | 对数模型 | 指数模型 | 幂函数模型 | 平方根模型 | 双曲线模型 | |||||||||
| 预测值/mm | 误差/% | 预测值/mm | 误差/% | 预测值/mm | 误差/% | 预测值/mm | 误差/% | 预测值/mm | 误差/% | ||||||
| 15 | -18.03 | -17.32 | -3.94 | -18.22 | 1.05 | -18.42 | 2.16 | -19.02 | 5.49 | -19.10 | 5.93 | ||||
| 12 | -19.42 | -19.66 | 1.24 | -19.18 | -1.24 | -20.85 | 7.36 | -21.23 | 9.32 | -20.12 | 3.60 | ||||
| 9 | -21.90 | -22.54 | 2.92 | -22.39 | 2.24 | -20.75 | -5.25 | -20.45 | -6.62 | -21.30 | -2.74 | ||||
| 6 | -25.38 | -26.45 | 4.22 | -24.90 | -1.89 | -27.47 | 8.23 | -26.74 | 5.36 | -26.55 | 4.61 | ||||
| 3 | -31.98 | -33.15 | 3.66 | -32.61 | 1.97 | -34.02 | 6.38 | -34.90 | 9.13 | -33.65 | 5.22 | ||||
| 0 | -36.71 | -35.48 | -3.35 | -36.66 | -0.14 | -35.78 | -2.53 | -38.26 | 4.22 | -38.37 | 4.52 | ||||
从表 3和表 4可知,各回归参数模型最终沉降量与观测值比较接近,其中指数模型的预测误差最小,最大误差仅为2.24%,对数模型和双曲线模型次之,最大误差分别为4.23%和6.24%,幂函数模型和平方根模型预测误差稍大,分别为8.37%和9.88%,说明指数模型相比其他模型能较好地反映兰永线工程高填方路基的工后沉降规律。
5 结论(1) 半填半挖高填方路堤沉降随时间增加而增大,且填方高度较大的路肩位置沉降大于行车道位置沉降。
(2) 高填方路堤沉降稳定时间较长,路堤填筑结束1年后沉降速率变小。
(3) 高填方路堤沉降监测19个月后,路肩位置路堤顶面最大沉降量为51.02 mm,行车道位置路堤顶面最大沉降量为36.71 mm。
(4) 2015年12月至次年2月中旬路基的升高疑为冻胀,还需后续布置相关的监测设施进一步从试验角度验证。
(5) 在指数模型、幂函数模型、平方根模型、双曲线模型和对数模型中,对数模型能较好地反映高填方路基的工后沉降规律。
| [1] | 冯忠居, 曹文海. 软弱地基上高填方路堤沉降观测及数值分析[J]. 兰州理工大学学报, 2013, 39(2): 491-496 FENG Zhong-ju, CAO Wen-hai. Observation and Numerical Analysis of Settlement of High Filled Embankment on Soft Subgrade[J]. Journal of Lanzhou University of Technology, 2013, 39(2): 491-496 |
| [2] | 景宏君, 胡长顺, 王秉纲. 黄土高路堤沉降变形规律研究[J]. 岩石力学与工程学报, 2005, 24(增2): 5845-5850 JING Hong-jun, HU Chang-shun, WANG Bing-gang. Study on Settlement and Deformation Laws of High Loess-fill Embankment[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(S2): 5845-5850 |
| [3] | 黄涛, 刘辉. 强夯结合碾压控制高填方沉降的机理研究[J]. 西南交通大学学报, 2007, 42(2): 158-162 HUANG Tao, LIU Hui. Study on Mechanism of High Fill Settlement Controlled by Dynamic Compaction and Bedded-Earth Rolling[J]. Journal of Southwest Jaotong University, 2007, 42(2): 158-162 |
| [4] | 匡希龙, 邹德强. 基于龚帕斯曲线法的高填方路基工后沉降预测新思路[J]. 公路工程, 2008, 33(1): 127-129 KUANG Xi-long, ZOU De-qiang. A New Thought on Prediction Method for Settlement After Construction to High Embankment Based on Compertz Curve Method[J]. Highway Engineering, 2008, 33(1): 127-129 |
| [5] | 景宏君, 苏如荣, 苏霆. 高路堤沉降变形预测模型研究[J]. 岩土力学, 2007, 28(8): 1762-1766 JING Hong-jun, SU Ru-rong, SU Ting. Study of Settlement Deformation Prediction Model of High Embankment[J]. Rock and Soil Mechanics, 2007, 28(8): 1762-1766 |
| [6] | 王瑞甫, 陈华兴, 刘宏力. 高填方路基沉降计算方法研究[J]. 中外公路, 2007, 27(6): 14-16 WANG Rui-fu, CHEN Hua-xing, LIU Hong-li. Study of Method of Settlement Calculation of High Fill Embankment[J]. Journal of China & Foreign Highway, 2007, 27(6): 14-16 |
| [7] | 肖衡林, 李丽华, 郭小川, 等. 山区高填方路堤沉降预测方法[J]. 应用基础与工程科学学报, 2015, 23(1): 154-160 XIAO Heng-lin, LI Li-hua, GUO Xiao-chuan, et al. Settlement Predicted Method of High Filled Embankment in Mountain Area[J]. Journal of Basic Science and Engineering, 2015, 23(1): 154-160 |
| [8] | 王丽琴, 靳宝成, 杨有海. 黄土路堤工后沉降预测新模型与方法[J]. 岩石力学与工程学报, 2007, 26(11): 2370-2376 WANG Li-qin, JIN Bao-cheng, YANG You-hai. New Model and Method for Forecasting Post-construction Settlement of Loess-fill Embankments[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(11): 2370-2376 |
| [9] | 郑建国, 王婷, 张继文. 黄土路基沉降量预测方法的研究[J]. 岩土力学, 2010, 31(1): 321-325 ZHENG Jian-guo, WANG Ting, ZHANG Ji-wen. Study of Settlement Prediction Methods of Loess Subgrade[J]. Rock and Soil Mechanics, 2010, 31(1): 321-325 |
| [10] | 刘奉银, 赵然, 谢定义, 等. 黄土高填方路堤沉降分析[J]. 长安大学学报:自然科学版, 2003, 23(6): 23-28 LIU Feng-yin, ZHAO Ran, XIE Ding-yi, et al. Settlement of Loess-filled Highway Embankment[J]. Journal of Chang'an University:Natural Science Edition, 2003, 23(6): 23-28 |
| [11] | 孙笑, 赵明阶, 汪魁, 等. 长安综合试车场高填方路堤施工沉降控制数值模拟[J]. 重庆交通大学学报:自然科学版, 2012, 31(2): 257-260 SUN Xiao, ZHAO Ming-jie, WANG Kui, et al. Numerical Simulation on Settlements of Changan Comprehensive Test Track with High Fill Embankment[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2012, 31(2): 257-260 |
| [12] | 刘赪炜, 韩煊, 陈昌彦, 等. 高填方路基沉降预测的半数值半解析方法[J]. 地下空间与工程学报, 2011, 7(3): 491-496 LIU Cheng-wei, HAN Xuan, CHEN Chang-yan, et al. A Semi-analytical and Semi-numerical Method for Settlement Prediction to High Filling Embankment[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(3): 491-496 |
| [13] | 李华, 陈晨, 李向群. 压实度对高填方路基自身沉降影响的数值分析[J]. 铁道建筑, 2010(5): 85-86 LI Hua, CHEN Chen, LI Xiang-qiong. Numerical Analysis about Influence of Soil Compactness on High Filled Subgrade Subsidence[J]. Railway Engineering, 2010(5): 85-86 |
| [14] | 吴国雄, 曹竞荣, 丁静声, 等. V形冲沟超高路堤稳定性三维效应研究[J]. 中国公路学报, 2013, 26(1): 1-8 WU Guo-xiong, CAO Jing-rong, DING Jing-sheng, et al. Research on 3D Effect of V-shaped Gully on Super-high Embankment Stability[J]. China Journal of Highway and Transport, 2013, 26(1): 1-8 |
| [15] | 吕庆, 尚岳全, 陈允法, 等. 高填方路堤粘弹性参数反演与工后沉降预测分析[J]. 岩石力学与工程学报, 2005, 24(7): 1231-1235 LV Qing, SHANG Yue-quan, CHEN Yun-fa, et al. Back-analysis of Visco-elastic Parameters of Filling Materials and Settlement Prediction for High-filled Embankment[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1231-1235 |
| [16] | 刘宏, 李攀峰, 张倬元. 九寨黄龙机场高填方地基工后沉降预测[J]. 岩土工程学报, 2005, 27(1): 90-93 LIU Hong, LI Pan-feng, ZHANG Zhuo-yuan. Prediction of the Post-construction Settlement of the High Embankment of Jiuzhai-Huanglong Airport[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 90-93 |
| [17] | 高成雷, 赵文忠, 凌建明, 等. 山区公路半填半挖路基沉降控制指标与标准研究[J]. 岩土力学, 2014, 35(1): 151-158 GAO Cheng-lei, ZHAO Wen-zhong, LING Jian-ming, et al. Study of Index and Criterion for Settlement Control Applicable to Cut-and-fill Subgrade in Mountain-highway[J]. Rock and Soil Mechanics, 2014, 35(1): 151-158 |
| [18] | 王峰, 金武, 王宏坤, 等. 考虑侧向变形影响的客运专线路基沉降的修正[J]. 岩土工程学报, 2010, 8(增2): 245-248 WANG Feng, JIN Wu, WANG Hong-kun, et al. Amendment of Subgrade Settlement of Passenger Dedicated Line Considering the Lateral Deformation Effects[J]. Chinese Journal of Geotechnical Engineering, 2010, 8(S2): 245-248 |
 2017, Vol. 34
2017, Vol. 34
