扩展功能
文章信息
- 张光远, 庄河, 丁小东, 黄修莉, 王瑶
- ZHANG Guang-yuan, ZHUANG He, DING Xiao-dong, HUANG Xiu-li, WANG Yao
- 损失规避和缺货规避对订购行为影响的仿真试验分析
- Experimental Study on Impact of Loss Avoidance and Stockout Avoidance on Order Behavior Based on Simulation
- 公路交通科技, 2017, 34(2): 149-158
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 149-158
- 10.3969/j.issn.1002-0268.2017.02.023
-
文章历史
- 收稿日期: 2016-05-30
2. 西南交通大学 综合交通运输智能化国家 地方联合工程实验室, 四川 成都 610031;
3. 中国铁道科学研究院 运输及经济研究所, 北京 100081
2. Nation and Region Combined Engineering Lab of Intelligentizing Integrated Transportation, Chengdu Sichuan 610031, China;
3. Transport and Economic Research Institute, China Academy of Railway Sciences, Beijing 100081, China
不确定需求情况下,决策者受风险偏好、决策环境、管理经验等因素的影响,其实际决策行为将偏离理论模型。Whitin等[1]首次提出报童模型,用于解决需求波动情况下的库存决策问题,并成为需求不确定库存问题的经典模型。Fisher等[2]通过实证分析发现报童模型理论解和实际决策之间存在较大的偏差。Schweitzer等[3]通过设计行为试验证实了偏差,并提出低利润产品中决策者的实际订购量大于报童模型最优订购量,高利润产品中小于报童模型最优订购量。Lau等[4]对比分析了群体、个体订购行为,发现报童决策偏差现象在群体订购行为中表现得更为显著。基于上述研究,丁小东等[5]将决策者实际订购行为与报童模型最优解之间的偏差定义为报童决策偏差。
经典的报童模型假设决策者为风险中性、效用最大化,但在库存实践中,决策者的订购行为受各种决策偏差的影响,表现为有限理性。针对EUT的风险中性等假设,Kahneman 等[6-7]提出了损失规避理论。Schweitzer等首次将损失规避模型与报童模型相结合,发现损失规避决策者的订购量小于报童模型最优解。上述学者的研究中,缺货时对订购不足部分均不予惩罚。Wang等[8-9]认为缺货不仅会使决策者失去部分机会成本、流失顾客,甚至会影响企业信誉,应对订购不足的部分进行惩罚,并在Schweitzer等损失规避订购模型的基础上,研究了缺货惩罚下损失规避型决策者的订购行为。谭建[10]对Wang等的模型进行扩展,并对参数进行了灵敏度分析。上述学者将损失规避理论主要应用在库存决策研究中,而夏金娇[11]、龙雪琴[12]将损失规避理论扩展至交通出行行为研究。本文在经典报童模型基础上,引进缺货规避和损失规避因子,构建部分惩罚和完全惩罚下决策者订购行为模型,并采用仿真试验的方法,测算了缺货规避和损失规避参数的有效取值区间。
1 问题描述Schweitzer等以报童模型为理论基础,首次设计库存决策行为试验,其试验参数为:市场需求为D~U[0, 300], 零售价格p=12,期末残值s=0,将生产成本c<(p+s)/2=6(以c=3为例子)定义为高利润产品,将c>(p+s)/2(以c=9为例子)定义为低利润产品。试验结果表明,决策者的实际订购量将分布在需求分布均值和理论最优订购量之间。结合表 1可知,学者们通过大量的行为试验,进一步证实了决策者的实际订购行为与报童模型最优订购量之间存在偏差。报童决策偏差是近10 a库存决策领域的重要发现,反映的是决策者的实际订购行为与以报童模型为代表的理论优化模型之间的偏差。
2 基于损失规避库存订购行为 2.1 报童模型
报童每天早上从报社购进报纸零售,晚上将没有卖掉的报纸退回。假设每份报纸的购进价为c,零售价为p,退回价为s(p>c>s),每天的订购量为q。根据历史统计数据可知报纸每日需求量D的分布函数为F,概率密度函数为f。在理性情况下,报童的利润为πn(q,D),如式(1)所示:
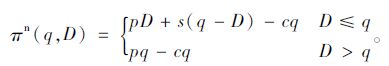
|
(1) |
报童的期望利润可表示为E[πn(q,D)],则关键分位点F(qn)如式(2)所示:
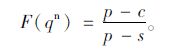
|
(2) |
考虑缺货成本时,受缺货规避偏差的影响,决策者将对订购不足部分[D-q]+进行惩罚,其中α>0为缺货惩罚系数,此时报童的利润πs(q,D)如式(3)所示:
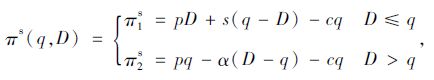
|
(3) |
期望利润E[πs(q,D)]=∫D=0∞πs(q,D)f(D)dD=∫D=0q[pD+s(q-D)f(D)]dD+∫D=q∞[pq-α(D-q)f(D)dD-cq=(p-s+α)[∫D=0qDf(D)-q·∫D=0qf(D)]+(p-c+α)q-αμ,在上式中分别对q求一阶导数、二阶导数,可得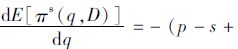
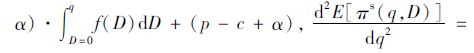
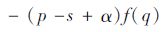
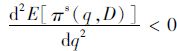
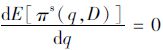
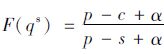
考虑缺货惩罚成本,式(3)中当D≤q时,令π1s=pD+s(q-D)-cq=0, 可得盈亏平衡点为D1=q(c-s)/(p-s): 当D∈[0,D1]时,报童处于亏损状态(π1s<0); 当D∈[D1,q]时,报童处于盈利状态(π1s>0)。同理,当D>q时,盈亏平衡点为D2=q(p-c+α)/α: 当D∈[q,D2]时, 报童处于盈利状态(π2s>0); 当D∈[D2,∞]时, 报童处于亏损状态(π2s<0)。
假设1:当D>q且D∈[D2,∞]时,令π2s=0。因此,D>q时,报童的利润函数为π2s=[π2s,0]+。
当D>q且D∈[D2,∞]时,出现订购不足现象,且决策者受缺货规避的影响其收益为负值(π2s<0)。然而,该情形下产品售尽,决策者不会认为其处于亏损状态,相比失去的机会成本收益甚微。因此,可假设此时决策者的收益为0,即令π2s=0。在Schweitze等的高利润场景中(U~[0, 300],p=12,c=3,s=0),如果决策者实际订购量为q=10,真实需求d=250,此时决策者的实际获益为πg=90,而决策者失去的机会成本为π1=2 160。若考虑缺货规避偏差,此时决策者的感知利润π2s<0,但此时产品售尽,决策者不会认为其处于亏损状态,只是较失去的机会成本其收益甚少,因此可假设此时π2s=0。由于D>q且D∈[q,D2]时,π2s>0,因此D>q时,报童的利润函数为π2s=[π2s,0]+。
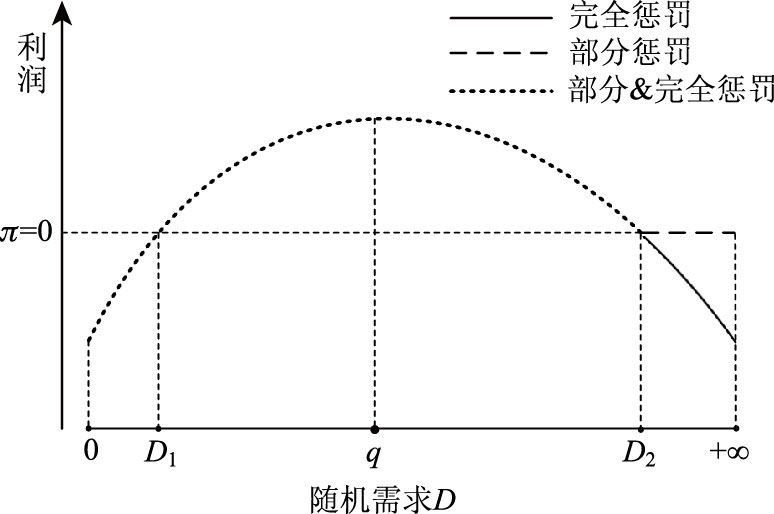
考虑缺货规避偏差,当D>q时,须对订购不足部分[D-q]+进行惩罚。如果对D∈[q,D2],D∈[D2,∞]均采用缺货规避的策略进行惩罚,可将此类策略称为完全惩罚策略;如果对D∈[q,D2]采用缺货规避的策略进行惩罚,当D∈[D2,∞]时采用假设1中的惩罚策略进行惩罚,可将此类策略称为部分惩罚策略。如图 1可知,当D∈[0,D2]时,完全惩罚、部分惩罚策略的利润函数曲线重合;当D∈[D2,∞]时,在完全惩罚策略下π2s<0,在部分惩罚策略下π2s=0。
|
| 图 1 不同惩罚策略下的利润函数 Fig. 1 Profit function under different punishment strategies |
| |
定义1:当D>q时,对订购不足部分[D-q]+进行惩罚:若决策者的感知利润满足假设1,该类惩罚策略即为部分惩罚;若决策者的感知利润满足式(3),则为全部惩罚策略。
由假设1可知,当D∈[0,D1]时,报童处于亏损状态,其利润为πL=∫D=0D1π1sdD; 当D∈[D1,∞]时,报童处于盈利状态,利润为πG=∫D=D1qπ1sdD+∫D=qD2π2sdD。 根据损失规避价值函数,可构建式(4)所示的价值函数表达式,其中损失规避系数λ≥1。
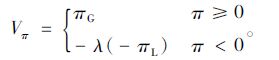
|
(4) |
(1) 部分惩罚策略下,决策者的订购模型
基于假设1和式(4)可得部分惩罚下,报童的期望效用U如式(5)所示:
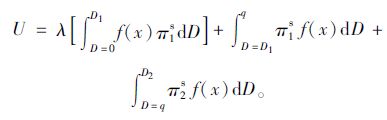
|
(5) |
在部分惩罚策略下,报童的利润函数为U=λ·∫D=0D1f(x)π1sdD+∫D=D1qπ1s f(x)dD+∫D=qD2π2s f(x)dD=(λ-1)∫D=0D1[pD-cq+s(q-D)]f(D)dD+∫D=0q[pD-cq+s(q-D)]f(D)dD+∫D=qD2[(p-c)q-α(D-q)]f(D)dD,对式中q求一阶导数,可得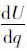
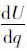

|
(6) |
(2) 完全惩罚下,决策者的订购模型
完全惩罚策略下,报童期望效用U′,如式(7)所示:
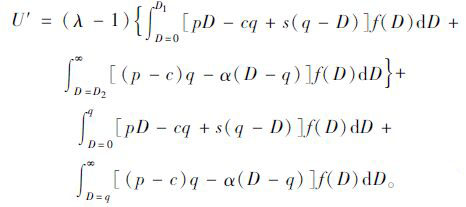
|
(7) |
当D∈[D2,∞]时,πs=π2s<0,则可得报童的期望效用U′=U+λ∫D=D2∞f(x)π2sdD= ∫D=D1qπ1sf(x)dD+∫D=qD2π2s f(x)dD+λ∫D=0D1f(x)π1sdD+λ∫D=D2∞f(x)π2sdD=∫D=D1q[pD-cq+s(q-D)]f(D)dD+∫D=qD2[(p-c)q-α(D-q)]f(D)dD+λ∫D=0D1[pD-cq+s(q-D)]f(D)dD+λ∫D=D2∞ [(p-c)q-α(D-q)]f(D)dD=(λ-1)∫D=0D1[pD-cq+s(q-D)]f(D)dD +∫D=D2∞[(p-c)q-α(D-q)]f(D)dD+∫D=0q[pD-cq+s(q-D)]f(D)dD+∫D=q∞[(p-c)q-α(D-q)]f(D)dD。 以上推理过程可知,完全惩罚下报童的期望效用为隐函数,无法直接求解最优解,因此,后文将采用仿真试验的方法求解最优解。
在式(7)中,令λ=1,对q求一阶导数、二阶导数,可得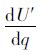
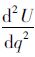
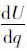
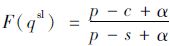
定理1:在缺货规避偏差的影响下,决策者的实际订购量要大于报童模型最优订购量。
证明: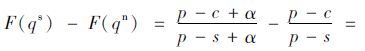

定理1表明在实际库存管理中,决策者不仅会因为缺货失去部分机会成本,还需面对由于需求未被满足而导致的客户流失、企业信誉下降等后果。因此决策者在实际库存决策时,通常受缺货规避偏差的影响,其实际订购量大于报童模型最优订购量,以降低缺货造成的损失。
推论1:假设市场需求为均匀分布D~U[a,b], 低(高)利润产品的生产成本为cL(cH), 报童模型的最优订购量为qLn(qHn), 考虑缺货规避时的最优订购量为qLs(qHs)。 决策者在低利润场景下将表现出更为显著的缺货规避偏差qLs-qLn>qHs-qHn。
证明:已知D~U[a,b],则qs=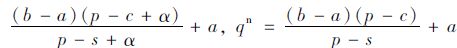
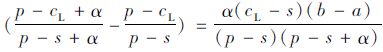
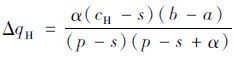
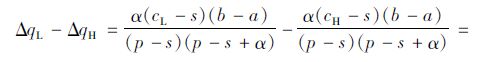
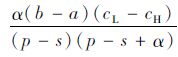
结合定理1、推论1可知,受缺货规避偏差的影响,决策者的实际订购量与报童模型最优订购量之间存在偏差,且实际订购量大于理论最优订购量,同时该偏差在低利润产品中表现得更为显著。由式(2)可知,低利润场景下最优订购量要小于高利润场景(qLn<qHn)。由于需求为均匀分布,则低利润场景下出现缺货的概率要大于高利润场景,因此决策者在低利润场景下表现出更显著的缺货规避偏差。
3.2 损失规避对订购行为的影响定理2:当不考虑缺货惩罚时,决策者受损失规避偏差的影响,其最优订购量ql如式(8)所示,ql小于报童模型最优订购量。
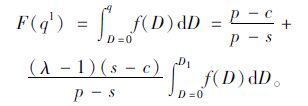
|
(8) |
证明:不考虑缺货惩罚时,报童的利润函数为E[πl(q,D)]=λ∫D=0D1[(s-c)q+(p-c)D]f(D)dD+
∫D=D1q[(s-c)q+(p-c)D]f(D)dD+(p-c)·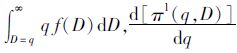
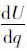
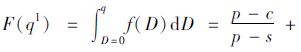

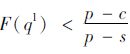
由式(4)可知,在损失规避的影响下,当π≥0时,损失规避系数λ=1;当π<0时,损失规避系数λ>1,这表明亏损带来的痛苦要大于获益带来的快乐,可见决策者实际感知到的效用要小于报童模型的最大期望利润,因此决策者的实际订购量小于报童模型的最优订购量。
推论2:假设市场需求为均匀分布D~U[a,b], 低(高)利润产品的生产成本为cL(cH), 报童模型的最优订购量为qLn(qHn), 考虑损失规避时最优订购量为qLl(qHl)。 决策者在高利润场景下将表现出更为显著的损失规避偏差,即qLn-qLl<qHn-qHl。
证明:已知D~U[a,b],则ql=∫D=aqf(D)dD=
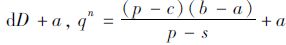
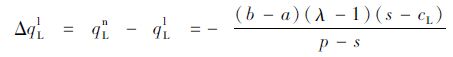
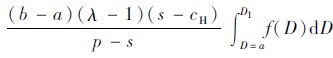
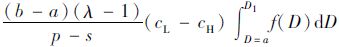
定理2表明,在损失规避偏差的影响下,决策者的实际订购量将小于报童最优订购量。同时由推论2可知,当D~U[a,b]时,相比报童模型最优订购量,决策者在低利润场景下订购量的减少量要小于高利润情况下,即损失规避偏差在高利润场景下表现得更为显著。
3.3 报童决策偏差的形成机制由定理1、定理2可知,在缺货规避(损失规避)的影响下,决策者的实际订购量将大于(小于)报童模型最优订购量。由推论1可知,缺货规避偏差在低利润产品中表现得更为显著,即低利润场景下决策者主要受缺货规避偏差的影响,其实际订购量将大于报童模型最优订购量。由推论2可知,损失规避偏差在高利润产品中表现得更为显著,即高利润场景下决策者主要受损失规避偏差的影响,其实际订购量将小于报童模型最优订购量。由上述定性分析可知,决策者在低利润场景下的实际订购量大于报童模型最优订购量,在高利润场景下的实际订购量小于报童模型最优解。因此,在缺货规避和损失规避的双重影响下,决策者的实际订购行为与报童模型最优订购量之间存在报童决策偏差。
定理3:假设市场需求为均匀分布D~U[a,b], 存在参数α>0,λ>1,使得在低利润产品中,当λL<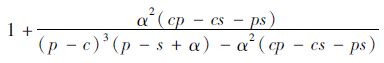
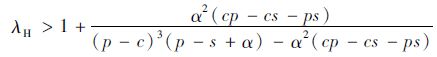
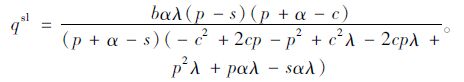
|
(9) |
证明:当D~U[a,b]时,U′=λ·∫D=aD1f(D)π1sdD+∫D=D1qπ1s f(D)dD+∫D=qD2π2s f(D)dD+λ·∫D=D2bπ2s f(D)dD=λ∫D=aD1[(p-s)D+(s-c)q]f(D)·dD+∫D=D1q[(p-s)D+(s-c)q]f(D)dD+∫D=qD2[(p+α-c)q-αD]f(D)dD+λ∫D=D2b[(p+α-c)q-αD]f(D)dD,dU′dq=λ∫0D1(s-c)f(D)dD+∫D1q(s-c)f(D)dD+∫D2q(p+α-c)f(D)dD+λ∫D1b(p+α-c)f(D)dD=1b[λ(s-c)D1+(s-c)(q-D1)+(p+α-c)(D2-q)+λ(p+α-c)(b-D2)]; 同理可得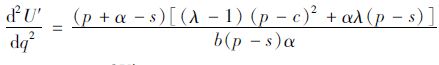
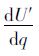

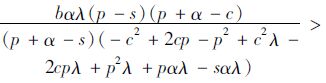
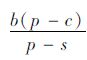
由定理3可知,当决策者受缺货规避和损失规避偏差的双重影响(即α,λ在一定的取值范围内)时,决策者在高利润产品中的实际订购量小于报童最优订购量,在低利润产品中大于报童最优订购量,这符合报童决策偏差的特征。在双重规避偏差的影响下,决策者最优订购量的表达式为隐函数,且十分复杂,无法求解参数的区间范围。本文将采用仿真试验的方法确定参数α,λ的取值范围。
4 仿真试验分析为验证本文提出的报童决策偏差现象,本文采用Schweitzer等的试验参数进行仿真试验。假设市场需求D~U[0, 300], 零售价格p=12,期末残值s=0,高(低)利润产品生产成本cH=3(cL=9)。 从式(2)可计算出高(低)利润产品的最优订购量为qHn=225(qLn=75)。下文的仿真试验中如没有特殊说明,均默认该试验参数。
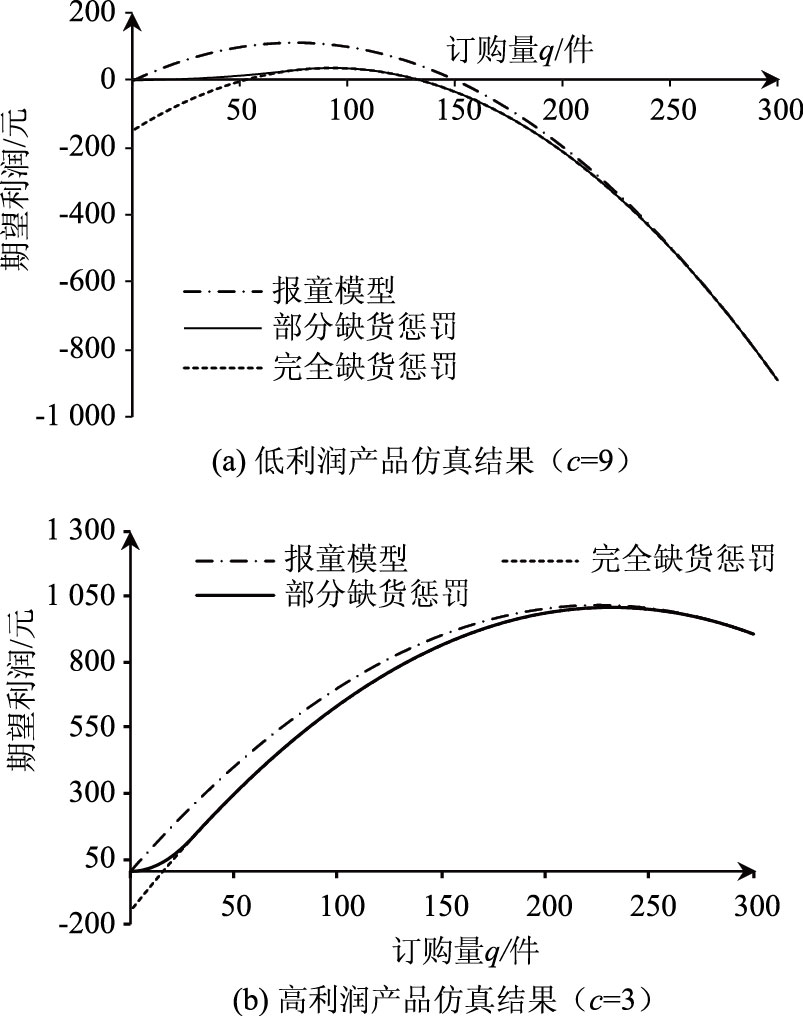
4.1 报童模型、部分惩罚、完全惩罚关系在对比报童模型与缺货惩罚之间的关系时,以缺货惩罚系数α=1为例,分别建立低利润、高利润产品仿真试验。如图 2(a)所示,在低利润场景中,当订购量q∈[70, 300]时,部分缺货惩罚期望利润U等于完全缺货惩罚的期望利润U′;当q∈[0,70)时,U>U′。 如图 2(b)所示,在高利润场景中,当订购量q∈[30,300]时,U=U′,当q∈[0,30)时,U>U′。 相比报童模型,缺货惩罚会降低决策者的期望利润。
|
| 图 2 部分缺货惩罚和完全缺货惩罚下的订购行为(α=1) Fig. 2 Order behaviors under fully-stockout-punishment and partial-stockout-punishment strategies(α=1) |
| |
图 2表明,部分与完全缺货惩罚策略对应的期望利润只在较小的范围内存在差异,且上述两个仿真试验中,报童模型最优订购量均分布在两种惩罚策略的期望利润无差异区间内(75∈[70,300],225∈[30, 300]), 这表明两种惩罚策略下,决策者的最优订购策略相同,即假设1不影响决策者的最优订购行为。
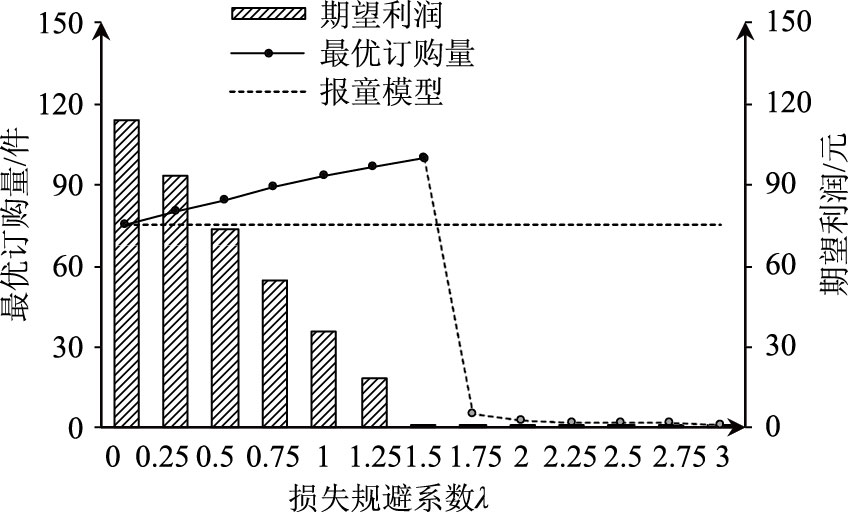
4.2 缺货规避对订购行为的影响从定理1可知,当决策者受缺货规避偏差影响时,其实际订购量将大于报童最优订购量。根据2.2节考虑缺货规避的库存决策模型,构建如图 3所示的仿真试验。如图 3所示,低利润场景中,当缺货规避系数α>1.5时,最优订购量小于5,决策者的期望利润趋近于0,此时决策者无利可图,表明惩罚成本过高,不符合现实情况。因此低利润场景下,规避系数的合理取值区间为α∈[0,1.5]。同理,在高利润场景中,构建类似的仿真试验,发现α∈[0,1.5]满足试验要求。因此在本文的仿真试验中,α的合理取值区间应为α∈[0,1.5],并在下文分别以α=0.5,α=1,α=1.5为例构建仿真试验。
|
| 图 3 缺货规避系数的取值范围(c=3) Fig. 3 Value scope of stockout avoidance coefficient(c=3) |
| |
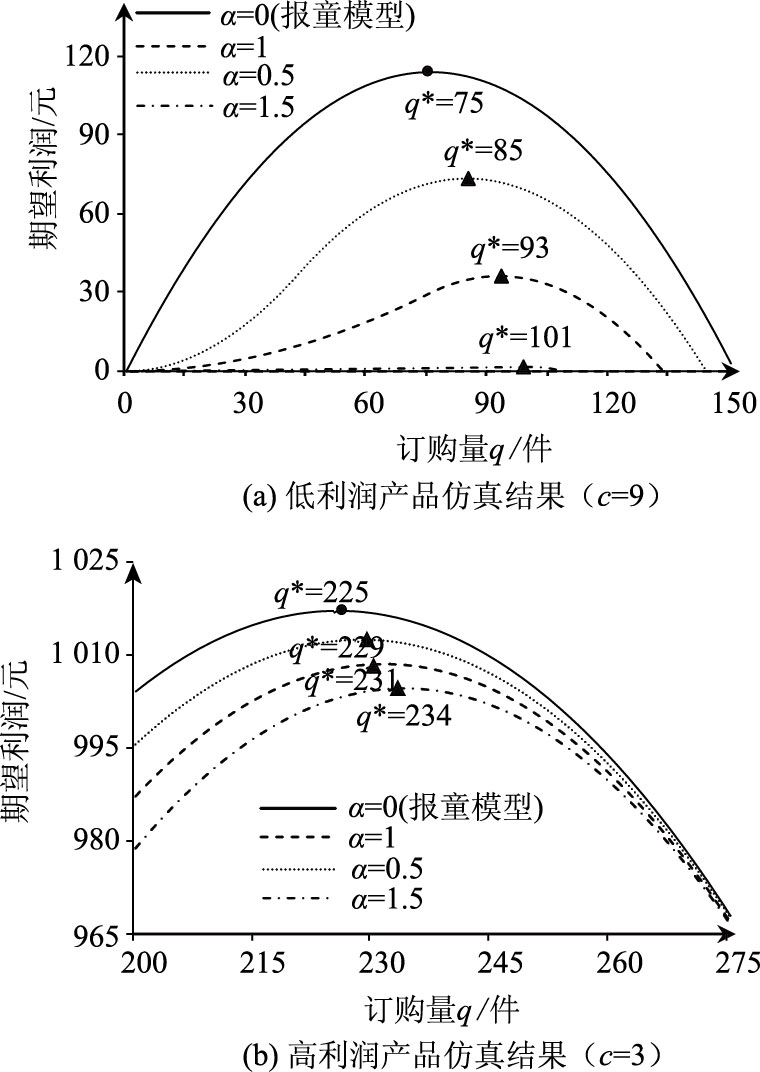
如图 4(a)所示,在低利润场景中,当α取0.5,1,1.5时,最优订购量分别为85,93,101,均大于报童模型最优订购量75,同时随着缺货惩罚系数的增加,决策者的最优订购量在不断增加。同理,如图 4(b)所示,在高利润场景中,受缺货规避偏差的影响,决策者的实际订购量均大于报童模型最优订购量。上述结果表明,决策者的最优订购量随着缺货规避系数的增大而增大。
|
| 图 4 缺货规避对订购行为的影响 Fig. 4 Impact of stockout avoidance on order behavior |
| |
从推论1可知,决策者在低利润和高利润产品中,均表现出缺货规避的订购行为,但在低利润产品中更为显著。从图 4所示的仿真结果可知,在低利润产品中,当缺货偏差由0增加至1.5时,其最优订购量由75增加至101,增量为26;在高利润产品中,当缺货偏差由0增加至1.5时,其最优订购量由225增加至234,增量为9。可见,低利润场景中,决策者对缺货更为敏感。该仿真试验中,需求为[0, 300]的均匀分布,低利润场景下,报童模型的最优订购量为75,需求被满足的概率为0.25·(75÷300),即出现缺货的概率为0.75(1-0.25);同理,高利润场景下出现缺货的概率为0.25。可见,低利润场景下出现缺货的概率更大,因此缺货规避行为在低利润产品中表现得更为显著。
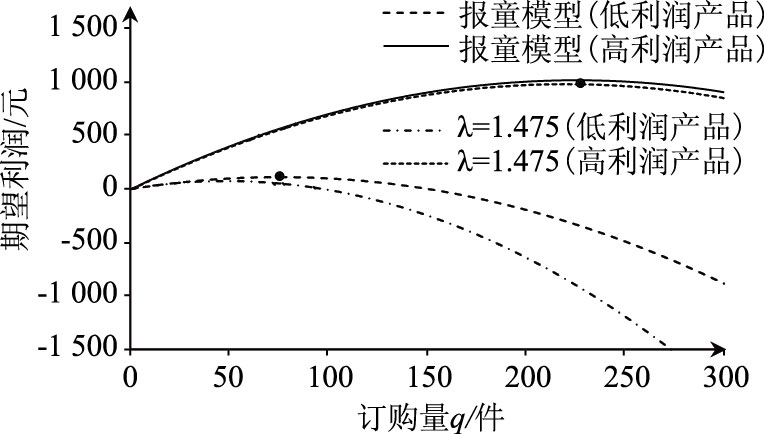
4.3 损失规避对订购行为的影响在式(5)中令α=0,构建低利润产品和高利润产品仿真试验。如图 5所示,在高利润场景中,当λ=1.475时,决策者的实际订购量与报童模型最优订购量相等(qH1.475=qHn=225)。从定理2可知,若1<λ1<λ2,则有qn≥qλ1≥qλ2。因此当1<λ≤1.475时,qHn≥qHλ≥qH1.475,有qHλ=225,即损失规避系数λ对决策者实际订购行为的影响不显著。因此本文在构建高利润产品仿真试验时,取λH>1.475。在低利润产品中,当λL=1.475时,决策者的最大期望利润仅为89,表明损失规避系数过大,不符合实际情况。从定理2可知,随着缺货规避系数的增大,决策者的最优订购量、最大期望利润将减小,即当λL>1.475时,决策者的最大期望将小于89。因此,本文在构建低利润产品中,损失规避偏差的合理取值为λL<1.475。
|
| 图 5 损失规避系数确定 Fig. 5 Determining loss aversion coefficient |
| |
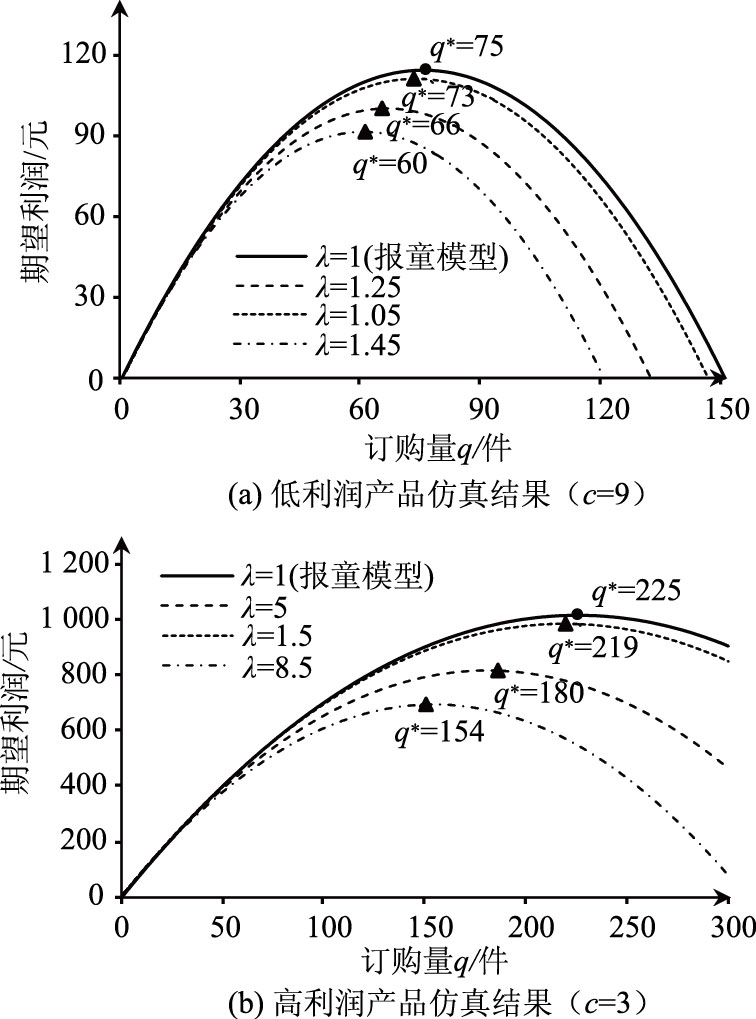
结合上述分析,本文在构建仿真试验时,以λ=1.475为分割点:在低利润产品中,取λL<1.475;在高利润产品中,则有λH>1.475。在实际仿真时,令λL∈[1.05,1.25,1.45],λH∈[1.5,5,8.5],结果如图 6所示。
|
| 图 6 损失规避对订购行为的影响 Fig. 6 Impact of loss avoidance on order behavior |
| |
由定理2可知,当决策者受损失规避影响时,其实际订购量小于报童模型最优订购量。如图 6(a)所示,在低利润产品中,当λ取1.05,1.25,1.45时,最优订购量分别为73,66,60,均小于报童模型最优订购量75。同理,在高利润产品中,当λ取1.5,5,8.5时,最优订购量分别为219,180,154,均小于报童模型最优订购量225。同时,决策者的最优订购量随着损失规避系数的增加而减小。
从推论2可知,决策者在低利润和高利润产品中均表现出损失规避的订购行为,但在高利润产品中更为显著。从图 6可知,低利润场景下,决策者最优订购量的波动区间为[60, 75],而需求的分布区间为[0, 300],即决策波动率为5%;高利润场景下,决策者最优订购量的波动区间为[154, 225],波动率为24%。由此可见,在高利润场景下,决策者的订购行为随着缺货规避系数的波动更为显著,即决策者在高利润场景下表现出更显著的损失规避行为。
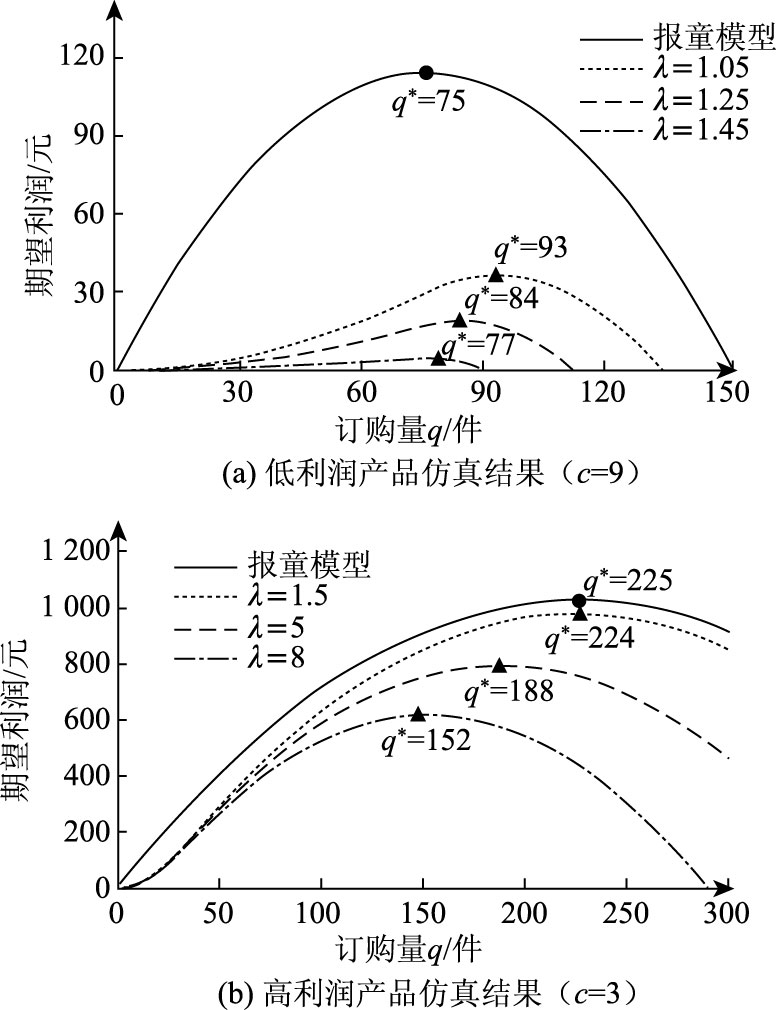
4.4 报童决策偏差形成机制为验证报童决策偏差的形成机制,本文结合式(5),令α=1(缺货规避系数α是一个经验参数,其反映由于供应短缺造成的企业信誉降低、顾客流失、失去潜在的利润等无形损失,需要而根据具体情况对其进行估计。),λL∈[1.05,1.25,1.45],λH∈[1.5,5,8.5]构建仿真试验,结果如图 7所示。
|
| 图 7 损失规避决策者最优订购量(α=1) Fig. 7 Loss aversion decision-maker's optimal quantity(α=1) |
| |
同时考虑缺货规避和损失规避,在低利润产品中,当α=1,λL∈[1.05,1.25,1.45]时,决策者实 际订购量均大于报童模型最优订购量,同时,随着损失规避系数增大,决策者的最优订购量、期望利润均减小;在高利润产品中,当α=1,λH∈[1.5,5,8.5]时,决策者的实际订购量均小于报童模型最优订购量,同时,随着损失规避系数增大,决策者的最优订购量、期望利润均减小。由上述仿真试验可知,决策者的缺货规避偏差和损失规避偏差可以解释报童决策偏差的形成机制。
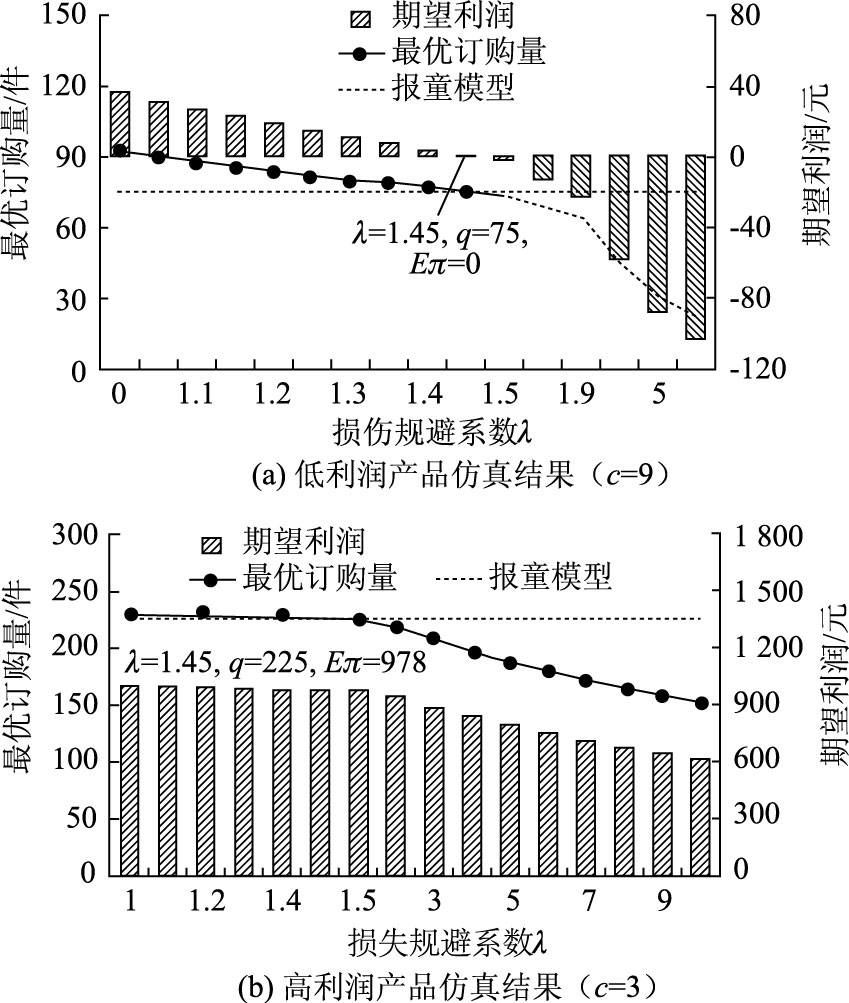
4.5 确定参数取值范围损失规避系数反映的是决策者对损失与获益的敏感系数。λ=1表明损失带来的痛苦等于(相同单位)获益带来的快乐;λ>1表明决策者对损失带来的痛苦更加敏感。Wu等[15]、曾建敏[16]通过大量试验测试了不同情况下损失规避系数的取值。为获得损失规避系数的取值范围,本文对上述试验进行扩展。如图 8(a)所示,在低利润产品中,当λL=1.45时,决策者的期望利润为0,同时订购量等于报童模型最优订购量;当λL>1.45时,决策者的期望利润均为负值,表明损失规避系数过大,不符合实际情况;当1 <λL<1.45时,E(πL)>0,决策者的最优订购量均大于报童模型最优订购量,该现象与报童决策偏差现象一致。综上所述,在低利润产中,损失规避系数的取值范围为λL∈(1,1.45)。
|
| 图 8 损失规避系数的取值范围(α=1) Fig. 8 Value scope of loss avoidance coefficient(α=1) |
| |
如图 8(b)所示,在高利润产品中,当λH=1.45时,决策者实际订购量等于报童模型最优订购量;当1<λH<1.45时,决策者的实际订购行为对λH的变化不明感,且qHsl>qHn,不满足报童决策偏差现象;当λH>1.45时,随着λH的增大,最优订购量、期望利润均显著减小,同时qHsl<qHn,满足报童决策偏差现象。Schweitzer等通过行为试验发现,高利润场景下决策者的订购量一般大于需求均值;再结合图 8(b)可知,当λH=10.5时,决策者的实际订购量为150。综上所述,高利润产品中,损失规避系数的取值范围为:λH∈(1.475,10.5)。
仿真试验结果表明,当α=1,λL∈(1,1.45],λH∈(1.45,10.5]时,决策者表现出报童决策偏差现象。结合定理3,可得出该仿真试验下α,λ参数组合,如表 2所示。
| α | 0.2 | 0.4 | 0.6 | 0.8 | 1 | 1.2 | 1.4 | 1.5 |
| λL | 1~1.01 | 1~1.05 | 1~1.13 | 1~1.25 | 1~1.45 | 1~1.77 | 1~2.41 | 1~3 |
| λH | 1.01~ 10.5 |
1.05 ~ 10.5 |
1.13~ 10.5 |
1.25~ 10.5 |
1.45~ 10.5 |
1.77~ 10.5 |
2.41~ 10.5 |
3~ 10.5 |
从图 9(a)可知,在低利润产品中,λL的取值区间随着α的增大而扩大,表明当决策者表现出较为显著的缺货规避心理时,其损失规避心理显著性增强;从图 9(b)可知,在高利润产品中,λL的取值区间随着α不断增大而缩小,表明当决策者表现出较为显著的缺货规避心理时,其损失规避显著性减弱。该结论表明,决策者在实际库存决策时,将同时受缺货规避偏差和损失规避偏差的双重影响,且二者之间相互影响,即低利润产品中二者之间为正向关系,在高利润产品中二者之间为反向关系,当λ,α的取值满足表 2所示参数组合时,决策者的订购行为将表现出报童决策偏差现象。

|
| 图 9 损失规避系数与缺货规避系数的关系 Fig. 9 Relationship between loss aversion coefficient and stockout avoidance coefficient |
| |
5 结论
采用仿真试验的方法,研究缺货规避、损失规避的角度研究报童决策偏差的形成机制,得到如下主要结论:(1)在缺货规避偏差(损失规避偏差)的影响下,决策者的实际订购量大于(小于)报童模型最优解;(2)在低(高)利润场景下,决策者表现出更为显著的缺货规避(损失规避)偏差;(3)在缺货规避和损失规避的双重影响下,决策者的订购行为表现出报童决策偏差的特征;(4)当市场需求为D~U[0, 300]时,缺货规避系数的有效区间为α∈[0,1.5], 损失规避系数的有效区间为λL∈(1,1.45),λH∈(1.45,10.5)。
在研究缺货规避偏差、损失规避偏差对决策者订购行为的影响时,假设市场需求为均匀分布,同时在确定试验参数的取值范围时,采用的是仿真试验的方法。接下来的研究将通过行为试验的方法,估计决策者缺货规避系数、损失规避系数的取值范围,并验证当需求分布为正态分布、三角分布、指数分布时,规避偏差对订购行为的影响。
| [1] | WHITIN T M. Inventory Control And Price Theory[J]. Management Science, 1955, 2 (1): 61-68 |
| [2] | FISHER M, RAMAN A. Reducing The Cost of Demand Uncertainty Through Accurate Response to Early Sales[J]. Operational Research, 1996, 44 (1): 87-99 |
| [3] | SCHWEITZER M E, CACHON G P. Decision Bias in the Newsvendor Problem With A Known Demand Distribution:Experimental Evidence[J]. Management Science, 2000, 46 (3): 404-420 |
| [4] | LAU N, HASIJA S, BEARDEN J N. Newsvendor Pull-to-center Reconsidered[J]. Decision Support Systems, 2014, 58 (2): 68-73 |
| [5] | 丁小东, 庄河, 徐菱, 等. 前景理论对报童决策偏差的适用性[J]. 控制与决策, 2016, 31 (5) : 853-862 DING Xiao-dong, ZHUANG He, XU Ling, et al. Applicability of Prospect Theory to Newsvendor Decision Bias[J]. Control and Decision, 2016, 31 (5): 853-862 |
| [6] | KAHNEMAN D, TVERSKY A. Prospect Theory:An Analysis of Decision Under Risk[J]. Econometrica, 1979, 47 (2): 263-292 |
| [7] | TVERSKY A, KAHNEMAN D. Advances in Prospect Theory:Cumulative Representation of Uncertaint[J]. Journal of Risk and Uncertainty, 1992, 5 (4): 297-323 |
| [8] | WANG C X, WEBSTER S. The Loss-averse Newsvendor Problem[J]. Omega, 2009, 37 (1): 93-105 |
| [9] | WANG C X. The Loss-Averse Newsvendor Game[J]. International Journal Production Economics, 2010, 124 (2): 448-452 |
| [10] | 谭建, 王先甲. 缺货惩罚下的损失厌恶报童模型[J]. 武汉大学学报:工学版, 2010, 43 (5) : 677-680 TAN Jian, WANG Xian-jia. Out of Stock Penalty and Loss Aversion Newsvendor Model[J]. Engineering Journal of Wuhan University, 2010, 43 (5): 677-680 |
| [11] | 夏金娇, 隽志才, 高晶鑫. 基于前景理论的出行路径选择行为[J]. 公路交通科技, 2012, 39 (4) : 126-131 XIA Jin-jiao, JUAN Zhi-cai, GAO Jing-xin. Travel Routing Behaviors Based on Prospect Theory[J]. Journal of Highway and Transportation Research and Development, 2012, 39 (4): 126-131 |
| [12] | 龙雪琴, 宋嘉骐, 王建军, 等. 面向有限理性决策的出行者行为研究[J]. 公路交通科技, 2016, 33 (5) : 105-110 LONG Xue-qin, SONG Jia-qi, WANG Jian-jun, et al. Study on Traveler's Behavior for Bounded-rational Decision-making[J]. Journal of Highway and Transportation Research and Development, 2016, 33 (5): 105-110 |
| [13] | BOSTIAN A, HOLT A, SMITH M. Newsvendor"Pull-to-Center"Effect:Adaptive Learning in a Laboratory Experiment[J]. Manufacturing & Service Operations Management, 2008, 10 (4): 590-608 |
| [14] | BOLTON G, ELENA K. Learning-by-doing in the Newsvendor Problem:A Laboratory Investigation of the Role of Experience and Feedbback[J]. Manufacturing & Service Operations Management, 2008, 10 (3): 519-538 |
| [15] | WU G, GONZALEZ R. Curvature of the Probability Weighting Function[J]. Management Science, 1996, 42 (12): 1676-1690 |
| [16] | 曾建敏. 实验检验累积前景理论[J]. 暨南大学学报:自然科学与医学版, 2007, 28 (1) : 44-47 ZENG Jian-min. An Experimental Test on Cumulative Prospect Theory[J]. Journal of Jinan University:Natural Science & Medicine Edition, 2007, 28 (1): 44-47 |
 2017, Vol. 34
2017, Vol. 34

 ,
,