扩展功能
文章信息
- 郭秀荣, 刘跃雄, 杜丹丰, 亓占丰, 王迎辉
- GUO Xiu-rong, LIU Yue-xiong, DU Dan-feng, QI Zhan-feng, WANG Ying-hui
- 柴油车排气尾管处尾气温度影响因素的理论计算与试验研究
- Theoretical Calculation and Experimental Study on Influencing Factors of Temperature at Tail Pipe of Exhaust System of Diesel Vehicle
- 公路交通科技, 2017, 34(2): 135-142
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 135-142
- 10.3969/j.issn.1002-0268.2017.02.021
-
文章历史
- 收稿日期: 2016-01-26
机动车所排尾气中的主要污染物有HC,CO,NOx和PM等,其中HC和CO主要来源于汽油车,而NOx和PM 则主要来源于柴油车,尤其是重型柴油车[1]。Kirchstetter 等所做的一项测量显示,重型柴油车所排放的PM 值约为汽油车的24 倍[2]。目前颗粒捕集器(Diesel Particulate Filter,DPF)是净化尾气中PM最为简单有效的后处理方式之一[1, 3],随着欧Ⅵ排放法规的实施,柴油车已被强制要求装配DPF,使得DPF在柴油车排放后处理中愈发重要。微米木纤维作为DPF滤芯材料,与堇青石、金属丝网等滤芯相比,因其过滤效率高、排气背压小、取材广泛、成本低廉等优点体现出经济和环保的双重价值,有望成为新型柴油车尾气过滤材料。但微米木纤维的缺点在于不能长时间处于220 ℃以上高温环境,否则会被逐渐炭化,影响过滤效率,因此需将其放置在温度较低的排气系统尾管处[4-5]。然而尾管处尾气温度在高转速或大负荷时极有可能超过220 ℃,因而需要冷却器将尾气温度冷却至微米木纤维可承受的范围内。对于不同车型,由于其发动机型号和排气管路结构尺寸不同,其尾管处的排气温度也会有很大的差别,在研制冷却器时,需知道具体车型尾管处排气温度的变化范围及影响因素,有针对性地进行设计。目前,许多学者在柴油机涡轮增压器匹配和尾气温差回收利用等研究领域对尾气温度进行了相当丰富的讨论研究,但都是针对排气系统中排气歧管、排气管或消音器等某一部位进行的。例如,顾宏中[6]在涡轮增压柴油机性能研究中对涡轮增压器前的废气温度进行了探讨,并根据容积法提出了排温计算模型;H.Pucher等[7]研究了涡轮增压柴油机中排气能量的传输,并讨论排气能量对涡轮增压器的影响;张莉等[8]采用Navier-Stokes方程、标准k-ε方程模型对大型柴油集材车排气管内温度场进行模拟分析;李以农等[9]采用ANSYS CFX软件对排气消音器内部流场及温度场进行了模拟研究。
综合考虑排气系统各组件对排气尾管处温度影响的相关研究,对尾气余热利用及本研究后续的冷却器设计具有重要的意义。本文将根据排气温度计算模型——热平衡法模型(热力学第一定律修正模型)、一维稳态对流换热模型以及排气管系中的能量守恒,系统地研究整个排气系统不同组件处尾气温度,最终得到排气尾管处尾气温度的数值模型。
1 数值计算与试验 1.1 数值计算气缸中燃烧产生的废气经排气系统排出,由于热力学和气体动力学的综合作用,尾气总是以不稳定状态流动,整个尾气流场的温度分布极不均匀。发动机排气温度受诸多因素的影响,它不仅与气缸工作过程有关,而且与排气系统的结构尺寸有关。
本文对发动机排气系统进行简化,以试验用发动机台架为参照,不考虑副消音器及尾气净化装置,如图 1所示。尾气从排气歧管出来后,流经排气管直接到达主消音器,再经排气尾管排入大气。在尾气流动过程中,忽略因排气管结构引起的尾气流动变化,将排气管简化成直径为di的圆管。废气排放不但气流速度高,还伴随着一些化学反应,同时热量以热辐射和热传递等形式大量散发到大气中,散热过程极其复杂[10]。因此,本文对整个排气系统尾气温度的影响因素进行分段讨论。
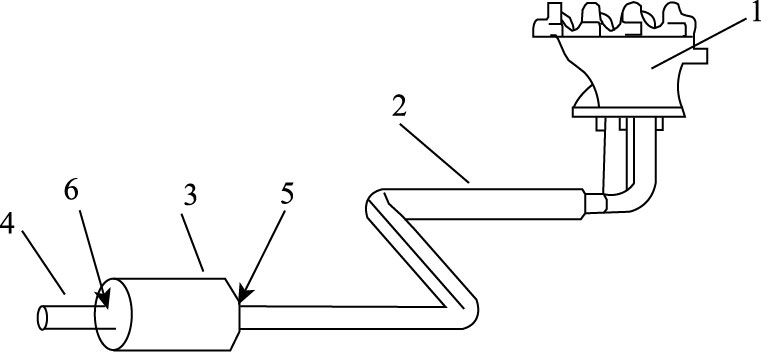
|
| 图 1 发动机排气系统简易结构图 Fig. 1 Simple structure diagram of engine exhaust system |
| |
1.1.1 排气歧管处尾气温度Tt
目前的排气温度计算理论主要有容积法、能量守恒法(热力学第一定律)、热平衡法(热力学第一定律修正法)。文献[11]的试验数据表明容积法较适合于发动机的低速工况,高速工况模拟误差较大,与实际值相比,模型计算值偏低;能量守恒法的计算结果误差较大,且误差值随转速升高而增大;热平衡法在低速工况下排温误差较大,但能正确反映排温变化趋势,但对于中高转速工况,计算值与试验值相比误差最小。因此,本文选用热平衡法计算柴油机排气歧管处尾气温度。根据文献 [7, 12],有:
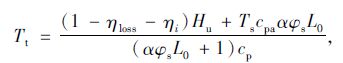
|
(1) |
式中,Tt,Ts分别为发动机排气歧管处温度和发动机进气温度;ηi为指示热效率;ηloss为冷却介质的散热系数; Hu为燃料低热值;cpa为空气平均定压比热容;cp为尾气比热容;L0为燃烧1 kg燃料理论上所需的空气量;α为过量空气系数;φs为扫气系数。
根据文献[13-14]中负荷特性台架试验的结果(指示热效率的图线变化趋势)以及指示热效率的经验取值范围(0.4~0.5),对有效功率和指示热效率的关系在MATLAB中进行拟合,得到一个指数函数如下:
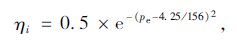
|
(2) |
式中pe为柴油机有效功率。
根据文献[15],有:
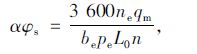
|
(3) |
式中,ne为额定工况转速; be为额定工况燃油消耗率; n为任意工况转速;qm为进气流量。
将式(2)和式(3)代入式(1),得排气歧管处尾气温度Tt:
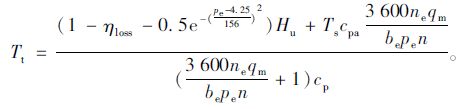
|
(4) |
从排气歧管到排气管,尾气的流速、成分和温度都会发生改变,并且尾气在管内由于气体流动压力波的影响,总是以不稳定状态流动;同时,尾气与外界的换热过程是以多种形式共同进行,包括热传导、热对流、热辐射等,使得尾气的热力计算过程相当复杂。本文中,对排气管简化并作以下假设[16]:
(1) 忽略流动中体积变化引起的温降;
(2) 气体沿径向传热,且管壁沿径向温度梯度为0;
(3) 气体在排气管内以稳态流动;
(4) 忽略尾气分子在排气管内摩擦做功的热量损失。
而且排气管道截面的横向尺度远小于纵向尺度,因此整个流动过程看作一维稳态传热,传热过程如图 2所示。
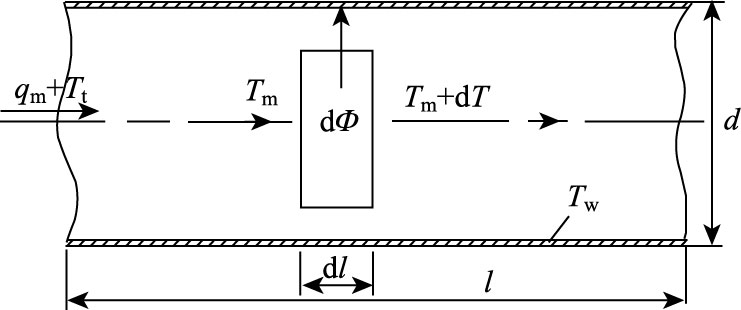
|
| 图 2 尾气微元管段热平衡示意图 Fig. 2 Schematic diagram of heat balance of micro-element pipe section |
| |
以微元管段dl为研究对象,根据牛顿冷却公式及能量守恒,微元段的尾气能量损失dφ可表示为[17]:
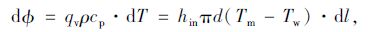
|
(5) |
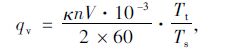
|
(6) |
式中,Tm为尾气在排气管长度方向任意一点处的温度;l为排气管长度;Tw为管壁温度;Ts为发动机进气温度;hin,hout为分别为管内、外对流换热系数;qv为尾气体积流率;d为排气管直径;ρ为尾气密度;V为发动机排量;n为转速;κ为充气效率和分子变更影响系数。
由式(5)~式(6)可导出排气管尾气温度沿轴向的分布:
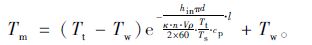
|
(7) |
以排气管壁为研究对象,忽略尾气在管内内能和势能的损失,则尾气、排气管壁和外界环境三者之间的热量交换都是以热传导、热对流和热辐射3种基本形式体现。由于排气管壁很薄,热传导热阻较其他两种形式相比较小,因此热传导可忽略不计。通过排气管壁进行的热量传递如图 3所示。
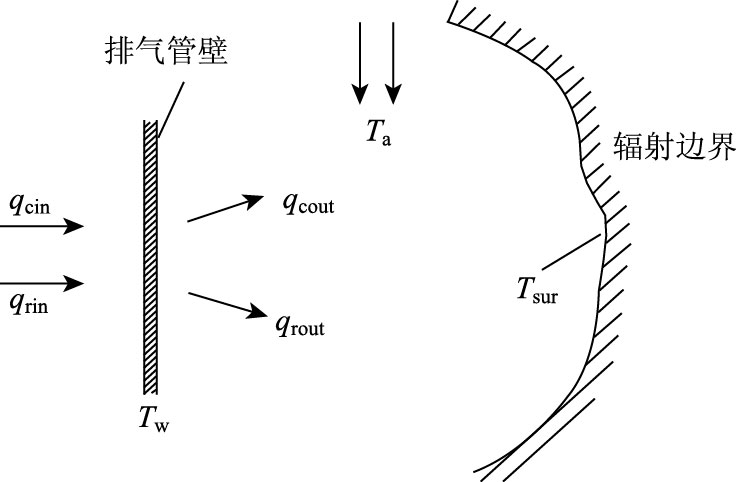
|
| 图 3 管壁热平衡示意图 Fig. 3 Schematic diagram of heat balance of pipe wall qcin—管内单位面积对流传热量;qcout—管外单位面积对流传热量;qrin—管内单位面积热辐射量;qrout—管外单位面积热辐射量;Ta—环境温度;Tsur—周围辐射温度。 |
| |
由牛顿冷却公式可知[17]:
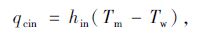
|
(8) |
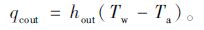
|
(9) |
假设管外辐射环境温度与周围空气温度相同,则管壁与外界环境单位面积热辐射量由史蒂芬-波尔兹曼定律可知[18]:
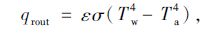
|
(10) |
式中,ε 为管壁的热发射率;σ为史蒂芬-波尔兹曼常数,σ=5.67×10-8 W/(m2·K4)。
管内热辐射属于有气体参加的热辐射,而气体中只有非对称结构的多原子气体有吸收和发射辐射的能力,因此尾气与管壁间的辐射换热只讨论水蒸气和二氧化碳。将管壁当作黑体看待,则管内单位面积的热辐射量[19]:
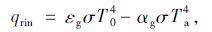
|
(11) |
式中,εg 为尾气热发射率;αg为尾气热吸收率。假设单位体积尾气中水蒸气占12%,二氧化碳占15%,εg和αg的具体计算参考文献[17, 19]。
根据单位面积热量守恒,排气管外壁向外界散出的热量等于排气管内壁吸收的热量:
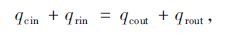
|
(12) |
即
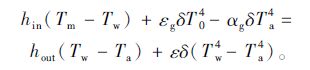
|
(13) |
根据式(7)和式(13)可求得Tm和Tw。
1.1.3 消音器后端尾气温度Tx排气消声器的作用是减少排气噪声和消除废气中的火焰及火星,使尾气安全地排入大气,它的直径往往数倍于排气管的直径。当尾气从排气管进入消音器以及从消音器中出来时,管道截面积发生突变,引起流动速度分布、大小等发生变化而产生局部损失,如图 4所示。
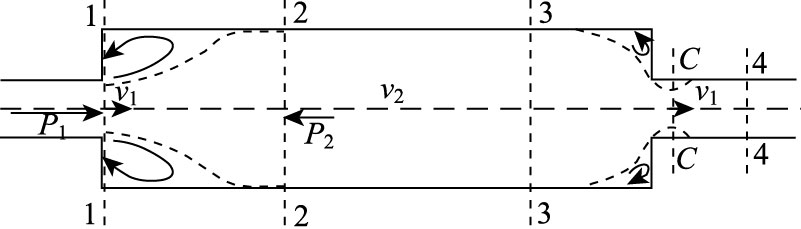
|
| 图 4 管道截面突变示意图 Fig. 4 Abrupt change of cross-section of pipe |
| |
管道截面大小突然发生变化时,必然出现气流边界层与管壁脱离的现象,在尾气主流和管壁之间形成旋涡区。由于漩涡的作用,尾气微团之间会产生摩擦和碰撞,并不断更新,因而连续不断地消耗主流的机械能,使得一部分机械能不可逆地转换为热能而散失[20]。
流体截面突然增大时,取刚开始增大的1-1截面和流速恢复正常的2-2面作为两个计算截面,根据伯努利方程,单位体积流体的能量损失hw(J/m3) 为[21]:
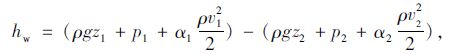
|
(14) |
式中,ν1,ν2为分别为尾气在排气管内和消音器内的流速;g为重力加速度;p1为排气管内压强;p2为消音器内压强;z1,z2分别为1-1,2-2截面的离地高度;α1,α2分别为管内和消音器内的动能修正系数。
因消音器水平放置,则z1=z2,式(14)可简化为:
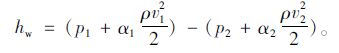
|
(15) |
两截面流体沿流动方向的动量方程[21]:
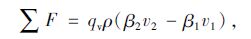
|
(16) |
式中,β1,β2分别为管内和消音器内的动量修正系数;∑F为沿轴向作用在流体段上的全部外力之和,包括:
(1) 1-1截面上的总压力,Fp1=p1A2;
(2) 2-2截面上的总压力,Fp2=p2A2,
式中,A1,A2分别为排气管和消音器的横截面积。
(3) 略去尾气与管壁的摩擦力,则动量方程可写成:
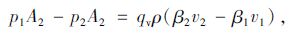
|
(17) |
式中体积流量qv=v2A2。
将式(17)代入(15)可得:
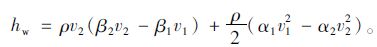
|
(18) |
对湍流,动能修正系数α1=α2≈1,动量修正系数β1=β2≈1[22]。利用连续性方程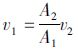
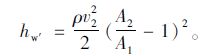
|
(19) |
流体截面突然缩小时,在断面C-C及其附近产生旋涡区,根据经验公式[23],其阻力系数:
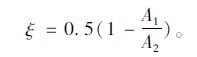
|
(20) |
忽略该段的沿程损失,则管道截面突然缩小时引起的能量损失hw″[23]:
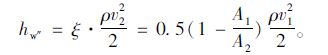
|
(21) |
根据连续性方程,管路中流经各管段的流体流量保持不变,管路中总的能量损失等于各管段的能量损失之和:
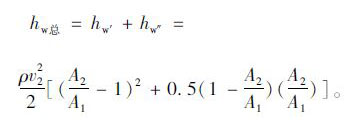
|
(22) |
同时,尾气与外界进行对流换热产生能量损失:
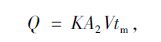
|
(23) |
式中,K为总传热系数;Vtm为消音器段尾气与外界环境间的对数平均温差。
根据能量守恒定律[17],有:
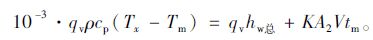
|
(24) |
因此,尾气经过消音器后的温度Tx为:
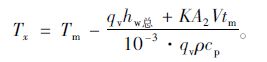
|
(25) |
由于排气尾管通常较短,在计算中可忽略其对尾气温度的影响,因此排气尾管处温度数值计算模型由式(4)、式(7)和式(25)可导出:

|
(26) |
为了验证尾气温度数值计算方法的准确性,需进行柴油机台架试验。试验装置如图 5所示,其中排气管长度可变。

|
| 图 5 台架试验装置的总体结构 Fig. 5 Overall structure of bench test apparatus 1—油耗仪;2—JX493ZLQ3A柴油机; 3—电涡流测功机;4—战旗2030消音器;5—热电偶温度传感器;6—排气管(按照不同长度要求,可更换); 7—计算机;8—FC2000发动机测控系统 |
| |
试验在空气相对湿度为(50±15)%、标准大气压 101.3 kPa 的环境下进行。发动机开始工作后,使其以怠速稳定运转20 min,保证尾气与管壁间达到热平衡,再进行温度测量。通过FC2000发动机测控系统调节发动机转速和扭矩。在同一工况下每隔1 min 记录一次,共记录5次,取平均值作为该工况下的温度值。测量下一工况时,先调至该工况稳定运行10 min后再开始测量。
2 结果与分析 2.1 模型参数选择根据推导出的排气温度数值计算模型,发动机转速、扭矩、环境温度、排气管直径和长度以及消音器尺寸等参数都直接影响排气尾管处的尾气温度。本文利用MATLAB对JX493ZLQ3A柴油机进行排气温度数值计算和分析。假设排气过程中气缸内压力、温度都各处相等,其扫气效率、指示热效率和散热损失系数可根据文献[8]确定。进行数值计算时使用的具体参数如表 1所示。
| 参数 | 参数值 | |
| 缸数 | 4 | |
| 排量/L | 2.771 | |
| 扫气系数 | 0.8 | |
| 排气管内径/m | 0.05 | |
| 消音器长度/m | 0.42 | |
| 燃烧低热值/ (kJ·kg-1) |
44 100 | |
| 空气比热容/ [kJ·(kg·K)-1] |
1.005 | |
| 额定转速/(r·min-1) | 3 600 | |
| 最大功率/kW | 75 | |
| 最大扭矩(2 200 r/min)/ (N·m) |
240 | |
| 散热损失系数 | 0.2 | |
| 消音器横截面积/m2 | 0.09 | |
| 尾气比热容/ [kJ·(kg·K)-1] |
1.097 | |
| 额定工况燃油消耗率/ [kg·(kW·h)-1] |
230 |
2.2 柴油车尾管处尾气温度影响因素分析 2.2.1 负荷对尾气温度的影响
当转速为 2 500 r/min、室内温度为20 ℃、排气管长度为2 m时,将表 1中的参数代入式(26),并将该条件下负荷与尾气温度的试验数据拟合,得到发动机负荷对尾气温度的影响如图 6所示。
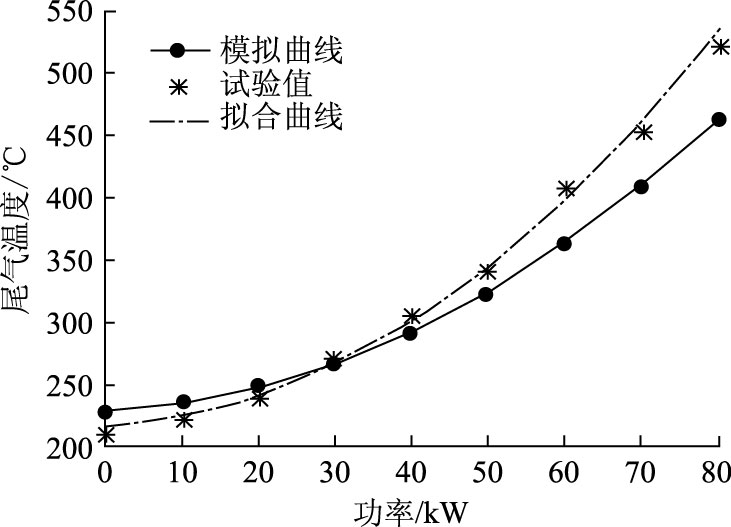
|
| 图 6 尾气温度随负荷的变化曲线 Fig. 6 Curves of exhaust gas temperature varying with load |
| |
由图 6可以看出,排气尾管处温度随负荷增大而升高;随着负荷的增大,数值模拟曲线上升的速率也随之增加。同时通过对比可以发现,当负荷逐渐增大时,模拟值与试验值的误差也越来越大。当转速一定时,柴油机负荷增大,每循环的供油量增加,产生的热量也增加,使尾气温度随负荷的增加而升高。当功率上升到一定程度,柴油机在高负荷下运转时,由于过量空气系数的持续减小,导致混合气形成和燃烧恶化,引起燃烧完善程度下降,而模拟计算中没有考虑到过量空气系数的变化,使得尾气温度的试验值与模拟值有较大的误差。
2.2.2 转速对尾气温度的影响由于该柴油机怠速时转速在800 r/min左右,将从900 r/min开始对尾气温度模拟。当扭矩为120 N·m,室内温度为20 ℃,排气管长度为2 m时,将表 1中的参数代入式(26),并将该条件下转速与尾气温度的试验数据拟合,可得出转速对尾气温度的影响如图 7所示。
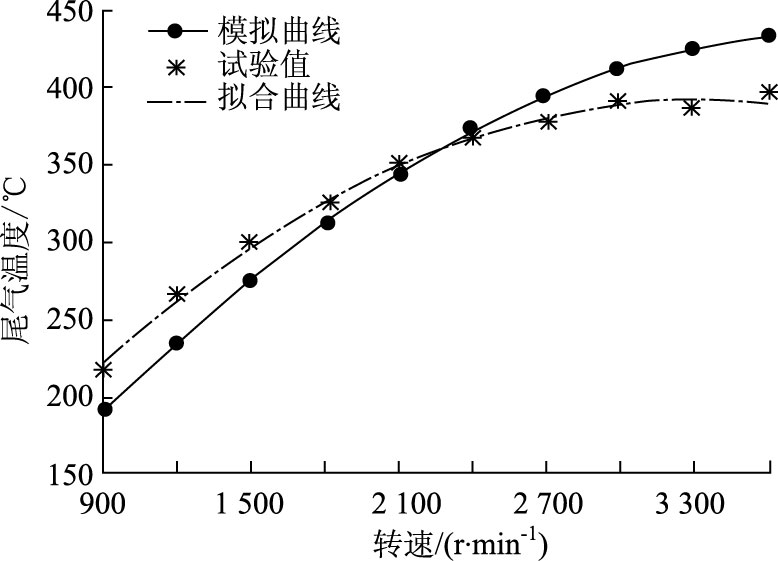
|
| 图 7 尾气温度随转速的变化曲线 Fig. 7 Curves of exhaust gas temperature varying with rotational speed |
| |
由图 7可以看出,排气尾管处温度随转速的增加而升高,并且随着转速增加,尾气温度逐渐趋于稳定。由试验数据可知,当转速到达3 000 r/min后,尾气温度没有明显变化。当发动机扭矩一定时,随着转速的增加,单位时间内参与燃烧的混合气体数量增多,每工作循环内燃烧产生的热量会增加,从而使尾气温度升高。同时,尾气流速也会增加,尾气与管外的换热强度增强,散热量快速增加,尾气温度慢慢趋于平衡。在图 7中,将试验值与模拟值对比可以发现,当转速在2 200 r/min时,随着转速增加或减小,误差均逐渐增大,使得发动机在低转速和高转速时,有较大的误差。这是由于在发动机转速越低时,热力学第一定律修正模型计算出的排气门尾气温度误差比较大,从而对整个数值计算过程产生了较大的影响;在高转速工况时,燃烧室内紊流强度更大,火焰传播速度迅速提高,同时排出的尾气流速更快,在排气管系中的尾气以更复杂的多维非稳态形式流动,换热过程复杂多变,与数值模型中的一维稳态传热会有较大的差别,因而在高转速时,试验值与理论值会有较大误差。
2.2.3 环境温度对尾气温度的影响高温管路一直与周围大气进行热交换,由式(9)可知,排气管外对流换热受环境温度的影响,因而,本文就环境温度对管内气体温度的影响规律和影响程度进行了探讨。当排气管长度为2 m,发动机在120 N·m,2 500 r/min工况下运转时,环境对尾气温度的影响规律如图 8所示。
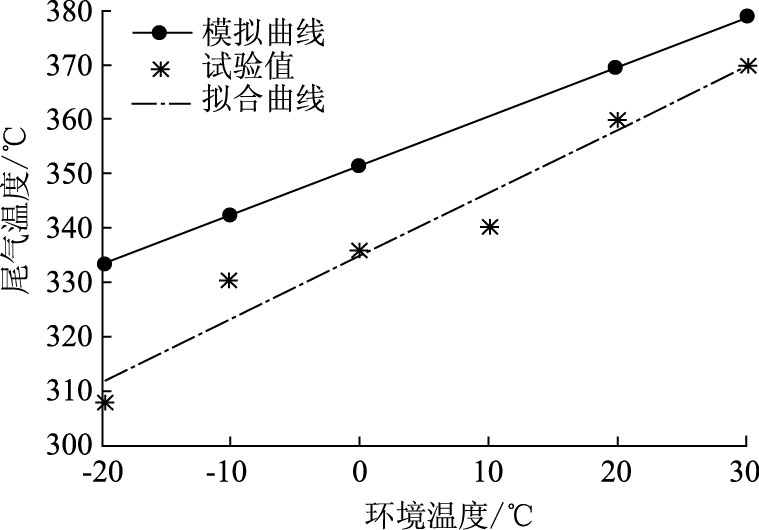
|
| 图 8 尾气温度随环境温度的变化曲线 Fig. 8 Curves of exhaust gas temperature varying with environmental temperature |
| |
由图 8可以看出,尾气温度随周围环境温度升高而升高,呈线性关系。这是由于在数值模拟中,忽略了热辐射的影响,由式(13)可知,尾气温度与环境温度的关系简化成了一次函数。从图中还可看出,环境温度越低时,误差越大。由于在进行试验过程中,柴油机散发的热量也会影响到柴油机周围大气温度,环境温度越低,受到的影响程度越大,因此环境温度越低时,模拟值与试验值的误差越大。
2.2.4 排气管长度对尾气温度的影响排气管定义为从排气歧管到消音器这一段管路。排气管长度为0时的尾气温度,即排气歧管处的尾气温度。试验中,进行了排气管长度分别为1,2,3,4 m和5 m这5组试验。将所得数据用MATLAB拟合,可得出环境温度为20 ℃,发动机在100 N·m,2 500 r/min 工况下运行时,排气管长度对尾气温度的影响如图 9所示。
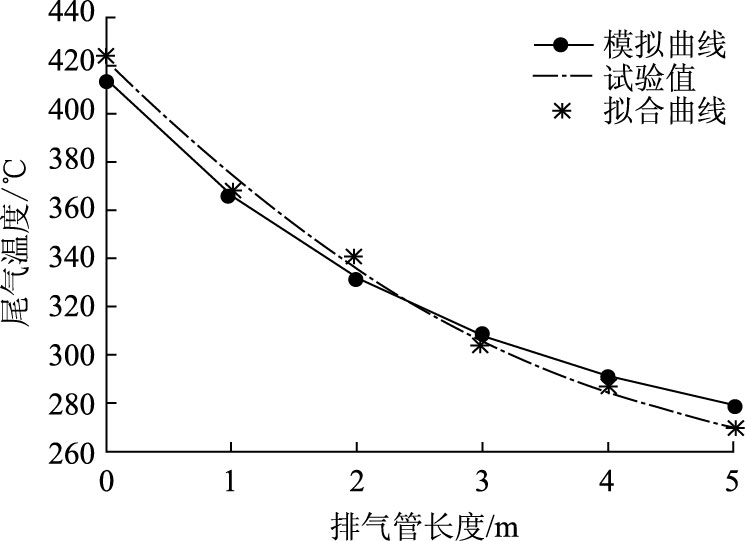
|
| 图 9 尾气温度随排气管长度的变化曲线 Fig. 9 Curves of exhaust gas temperature varying with length of exhaust pipe |
| |
由图 9可以看出,尾气温度随排气管长度的实际变化趋势与数值模型模拟的温度变化趋势基本相符,尾气温度随着排气管长度增加而降低,尾气温度下降的速率随着长度增加而变小。由于排气管长度增大,排气管的散热面积增大,单位时间内的换热强度增加,因此散热量增加,尾气温度下降。同时尾气温度下降,使得尾气与管外的对流换热强度下降,散热量减少,尾气温度的下降速率也就随之减少。
3 结论根据热力学第一定律修正模型、能量守恒以及一维稳态管对流换热模型,得出排气尾管处温度的数值模型。并以JX493ZLQ3柴油机为研究对象,分析了负荷、转速、环境温度、排气管长度对排气尾管处尾气温度的影响关系。负荷和转速对尾气温度的影响最大,排气管长度次之,环境温度的影响相对最小。
试验表明,数值计算模型在高负荷低转速和高转速时误差较大,在发动机任一工况下,图 6~图 9中理论值与试验值的曲线变化趋势一致。根据尾气温度的数值模型可以为不同车型的微米木纤维DPF的冷却器设计提供理论依据,同时也可为尾气余热利用等相关研究提供理论和试验参考。
| [1] | 周磊, 王伯光, 汤大刚. 重型柴油车对空气质量的影响及其排放的控制[J]. 环境科学, 2011, 32 (8) : 2177-2183 ZHOU Lei, WANG Bo-guang, TANG Da-gang. Impact of Heavy-duty Diesel Vehicles on Air Quality and Control of Their Emissions[J]. Environmental Science, 2011, 32 (8): 2177-2183 |
| [2] | KIRCHSTETTER T W, HARLEY R A, KREISBERG N M, et al. On-road Measurement of Fine Particle and Nitrogen Oxide Emissions from Light-and heavy-duty Motor Vehicles[J]. Atmospheric Environment, 1999, 33 (18): 2955-2968 |
| [3] | 赵佳, 闫学东, 王江锋. 机动车尾气排放和扩散研究综述[J]. 公路交通科技, 2011, 28 (S1) : 147-153 ZHAO Jia, YAN Xue-dong, WANG Jiang-feng. Review of Studies on Vehicle Emission and Diffusion[J]. Journal of Highway and Transportation Research and Development, 2011, 28 (S1): 147-153 |
| [4] | GUO Xiu-rong, DU Dan-feng, WANG Feng-hu, et al. Study on Test Instrument and Filtration Theory of the Carbonized Micron Wood Fiber DPF[J]. Microporous and Mesoporous Materials, 2011, 142 (2): 655-660 |
| [5] | 张汉召.炭化微米木纤维微粒捕集器制造工艺及过滤机理研究[D].哈尔滨:东北林业大学,2011. ZHANG Han-zhao.Study on Manueacturing Process and Filtering Mechanism of Carbonized Miceon-wood Fiber Particulate Filter[D].Harbin:Northeast Forestry University,2011. |
| [6] | 顾宏中. 涡轮增压柴油机性能研究[M]. 上海: 上海交通大学出版社, 1998. GU Hong-zhong. Research on Performance of Turbocharged Diesel Engine[M]. Shanghai: Shanghai Jiaotong University Press, 1998. |
| [7] | PUCHER H.Transport of Technically Usable Exhaust Energy in Turbocharged Engines[C]//BIT-TU Berlin Symposium on Turbocharging Technology. Beijing:Beijing Institute of Technology Press,2006. |
| [8] | 张莉, 李鸥, 臧杰. 大型集材车冬季排气管内温度场数值解与模拟[J]. 东北林业大学学报, 2011, 39 (4) : 133-134 ZHANG Li, LI Ou, ZANG Jie. Simulation on Internal Temperature Field in Exhaust Pipe of Large Skidder in Winter[J]. Journal of Northeast Forestry University, 2011, 39 (4): 133-134 |
| [9] | 李以农, 路明, 郑蕾, 等. 汽车排气消声器内部流场及温度场的数值计算[J]. 重庆大学学报:自然科学版, 2008, 31 (10) : 1094-1097 LI Yi-nong, LU Ming, ZHENG Lei, et al. Numerical Simulation of the Flow and Temperature Fields in an Automotive Exhaust Muffler[J]. Journal of Chongqing University:Nalural Seience Edition, 2008, 31 (10): 1094-1097 |
| [10] | 杨世铭, 陶文铨. 内燃机学[M]. 北京: 高等教育出版社, 2006. YANG Shi-ming, TAO Wen-quan. Internal Combustion Engine[M]. Beijing: Higher Education Press, 2006. |
| [11] | 刘秋颖, 石磊, 李胜达, 等. 柴油机涡轮增压器匹配程序中排气温度预测模型的研究[J]. 内燃机与动力装置, 2011 (2) : 29-34 LIU Qiu-ying, SHI Lei, LI Sheng-da, et al. The Study of Exhaust Temperature Forecasting Models in Turbocharging Matching Program of Diesel Engine[J]. Internal Combustion Engine & Powerplant, 2011 (2): 29-34 |
| [12] | 李见波, 徐士鸣, 刘福森. 车速变化对吸收/压缩混合制冷循环的影响[J]. 吉林大学学报:工学版, 2013, 43 (2) : 291-297 LI Jian-bo, XU Shi-ming, LIU Fu-sen. Influence of Driving Speed on Absorption/Compression Hybrid Refrigeration Cycle[J]. Journal of Jilin University:Engineering and Technology Edition, 2013, 43 (2): 291-297 |
| [13] | 周龙保. 内燃机学[M]. 北京: 机械工业出版社, 2005. ZHOU Long-bao. Internal Combustion Engine[M]. Beijing: Mechanical Industry Press, 2005. |
| [14] | 吴建华. 汽车发动机原理[M]. 北京: 机械工业出版社, 2005. WU Jian-hua. Principle of Automobile Engine[M]. Beijing: China Machine Press, 2005. |
| [15] | 黄粉莲, 纪威, 周炜. 涡轮增压柴油机进气流量的计算与仿真[J]. 农业工程学报, 2013, 29 (3) : 62-68 HUANG Fen-lian, JI Wei, ZHOU Wei. Calculation and Simulation of Air Mass Flow for Turbocharged Diesel Engines[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29 (3): 62-68 |
| [16] | GALINDO J, LUJÁN J M, SERRANO J R, et al. Description of a Heat Transfer Model Suitable to Calculate Transient Processes of Turbocharged Diesel Engines with One-dimensional Gas-dynamic Codes[J]. Applied Thermal Engineering, 2006, 26 (1): 66-76 |
| [17] | 赵镇南. 传热学[M]. 北京: 高等教育出版社, 2002. ZHAO Zhen-nan. Heat Transfer[M]. Beijing: Higher Education Press, 2002. |
| [18] | 谈和平, 刘林华, 易红亮, 等. 计算热辐射学的进展[J]. 科学通报, 2009, 54 (18) : 2627-2637 TAN He-ping, LIU Lin-hua, YI Hong-liang, et al. Recent Progress in Computational the Rmal Radiative Transfer[J]. Chinese Science Bulletin, 2009, 54 (18): 2627-2637 |
| [19] | 高天, 潘克熠, 陈飞. 直喷式柴油机缸内气体辐射传热的研究[J]. 西安交通大学学报, 2006, 40 (3) : 302-306 GAO Tian, PAN Ke-yu, CHEN Fei. Investigation on In-cylinder Radiation from Gases in DI Diesel Engine[J]. Journal of Xian Jiaotong University, 2006, 40 (3): 302-306 |
| [20] | 孙琳.圆管突扩(缩)局部阻力试验及流场数值模拟[D].哈尔滨:东北农业大学,2010. SUN Lin.Experimental Study and Flow Field Numerical Simulation on Resistance of Pipe with Sudden Expansion or Contraction[D].Harbin:Northeast Agricultural University,2010. |
| [21] | 陈卓, 周萍, 梅炽. 传递过程原理[M]. 长沙: 中南大学出版社, 2011. CHEN Zhuo, ZHOU Ping, MEI Chi. Transfer Principle[M]. Changsha: Central South University press, 2011. |
| [22] | ABDELAL F F, HAHU G G, GHIAASIAAN S M, et al. Pressure Drop Caused by Abrupt Flow Area Changes in Small Channels[J]. Experimental Thermal and Fluid Science, 2005, 29 (4): 425-434 |
| [23] | 吴持恭. 水力学(上册)[M]. 北京: 高等教育出版社, 2007. WU Chi-gong. Hydraulics (Volume I)[M]. Beijing: Higher Education Press, 2007. |
 2017, Vol. 34
2017, Vol. 34

 ,
,