扩展功能
文章信息
- 张伟, 肖日东, 邓晶
- ZHANG Wei, XIAO Ri-dong, DENG Jing
- 基于遗传算法的动态模糊神经网络城市快速路入口匝道控制
- Dynamic Fuzzy Neural Network for Controlling Entrance Ramp of Urban Expressway Based on Genetic Algorithm
- 公路交通科技, 2017, 34(2): 129-134,148
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 129-134,148
- 10.3969/j.issn.1002-0268.2017.02.020
-
文章历史
- 收稿日期: 2016-05-06
2. 中国公路工程咨询集团有限公司, 北京 100083
2. China Highway Engineering Consulting Corporation, Beijing 100083, China
随着我国经济的发展,汽车保有量增加,交通流量也随之不断增长[1-2],城市道路交通拥挤和事故发生率也逐渐升高。城市道路中起着主导性作用的城市快速路[3],也正面临着巨大的挑战。入口匝道控制是解决城市快速路交通拥挤最为有效的措施之一,因此寻找智能的、满足车流动态变化需求的入口匝道控制方法,对缓解城市快速路乃至整个城市道路交通拥挤状态有着重要意义[4]。
入口匝道控制的成功应用,从最早应用于美国的Zone算法,到后来应用于巴黎、阿姆斯特丹等地方的ALINEA算法[5],距今已将近有46年历史。经过多年实践,Zone算法及ALINEA算法具有其一定适用性,但由于当时没考虑到交通流的动态突变情况以及入口匝道排队的回溢现象,随着时间的推移,这两种算法的短板逐渐显现[6-7]。当前国内外学者正研究把自适应模糊控制算法[8-9]、神经网络控制算法[10]、遗传算法应用于智能交通控制领域[11-12],但各算法都有其缺点,因此控制算法的改善备受交通控制领域专家的关注。本文在前人应用于入口匝道的控制算法研究的基础上,以提高城市快速路利用率及服务水平为目的,提出具有递归环节的动态模糊神经网络实现城市快速路的入口匝道智能控制,并采用遗传算法对控制器参数进行优化,把模糊算法、神经网络、遗传算法综合应用于城市快速路的入口匝道控制中,最后选取北京某段城市快速路进行仿真分析,验证该方法对入口匝道的控制效果。
1 入口匝道模型为了在仿真中研究动态模糊神经网络控制算法的有效性,以及该算法与传统算法的比较,有必要推导一个城市快速路入口匝道的数学模型。
如图 1所示,选取一个路段宽度为Δx、主线的车道数目为λ的城市快速路路段。

|
| 图 1 城市快速路入口匝道 Fig. 1 Urban expressway entrance ramp |
| |
由交通流机理可以推导出:
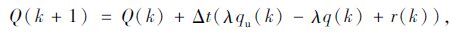
|
(1) |
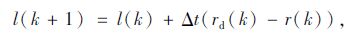
|
(2) |
式中,Q为路段内车辆总数;l为入口匝道排队车辆数目;Δt为采样时间。
通过方程(1)除以λΔx可以得到:
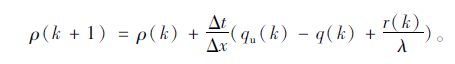
|
(3) |
通过大量的研究及实践证明,交通流密度ρ和交通流量可通过一定的函数关系式解析两者的联系,选取现在广泛应用于交通工程领域的LWR模型[13-15]:
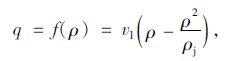
|
(4) |
式中,vl为城市快速路的自由流速度;ρj为城市快速路的阻塞密度。
将式(4)代入式(3)可得关系式:
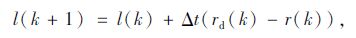
|
(5) |
由上面的交通流机理函数关系式推导,可得到城市快速路入口匝道控制的模型,如图 2所示。并且设定城市快速路入口匝道控制的状态方程:
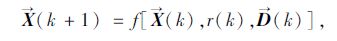
|
(6) |
式中,状态变量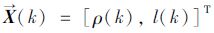
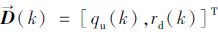

|
| 图 2 入口匝道控制模型 Fig. 2 On-ramp control model |
| |
2 城市快速路出入口匝道的动态模糊神经网络控制算法
由第1节推导的入口匝道控制模型可知交通流密度ρ是影响交通拥挤程度的关键参数,所以通过入口匝道调节,使城市快速路的交通流密度ρ尽量处于临界密度ρ临之下,以保证城市快速路的车辆行驶通畅,实现城市快速路的有效利用。
在保证不影响城市快速路正常使用的前提下,最大化地减短入口匝道的入口排队长度l,避免入口匝道发生回溢现象,精确地计算出入口匝道调节率r。如图 3所示,输入匝道的当前状态X,经过动态模糊神经网络控制算法的可调节特性优化系统,最终输出入口匝道调解率r。

|
| 图 3 入口匝道DFNN算法结构 Fig. 3 Structure of DNFF algorithm for on-ramp control |
| |
2.1 模糊规则的确定
根据交通流理论,城市快速路主线交通流密度ρ和入口匝道调解率r呈负相关,入口排队长度l和入口匝道调解率r呈正相关。城市快速路的主线交通对整个城市交通起着重要影响,因此选取主线交通流密度ρ为主要因素,入口匝道排队长度l为辅助因素。根据交通流参数特点,可得入口匝道模糊控制规则如表 1所示。
| r | ρ | |||
| 负(N) | 零(Z) | 正(P) | ||
| l | 负(N) | Z | Z | N |
| 零(Z) | P | Z | N | |
| 正(P) | P | P | N | |
动态模糊神经网络当中模糊词集的选取选择如下(对应交通状态:堵塞、正常、畅通):
{负(N),零(Z),正(P)}。
2.2 动态模糊神经网络文中设计的城市快速路的入口匝道动态模糊神经网络控制系统,在其神经网络内部引入递归环节,捕获入口匝道控制系统的动态响应,并利用遗传算法的全局寻优能力来训练该动态模糊神经网络。动态模糊神经网络(DFNN)的各个参数根据交通流机理及大量实践经验选择初始值,构建了一个动态映射网络。该控制系统比传统入口匝道控制系统更适于交通流不断变化的动态交通状况。
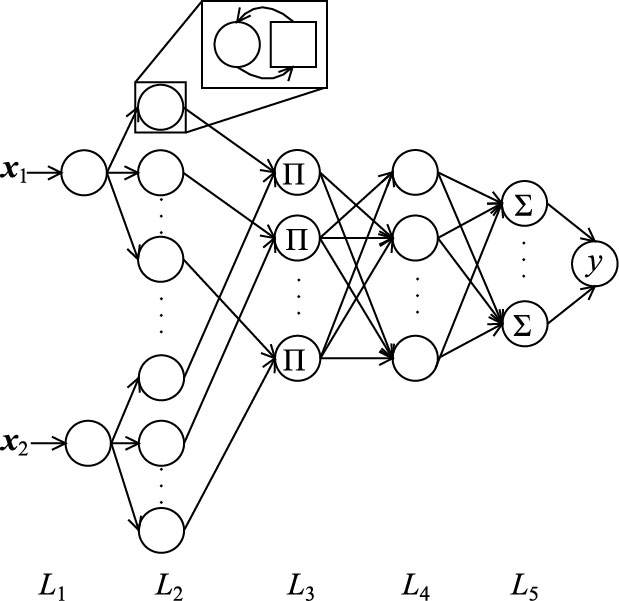
设计的入口匝道控制系统的多层递归动态模糊神经网络的拓扑结构如图 4所示,该结构一共由5部分组成。以下的描述中,uis和Ois分别表示第s层的第i个节点的输入和输出。
|
| 图 4 DFNN 的网络架构 Fig. 4 Network structure of DNFF |
| |
第1层为输入层L1:各个节点直接与输入向量x1(城市快速路交通流密度ρ)和x2(入口匝道排队长度l)相连,并将输入值X=[x1,x2]T传到下一层。

|
(7) |
第2层为模糊化加递归层(规则层)L2:每个神经元代表 2.1节模糊规则表中的一个语言变量值,即对应的交通状态:堵塞、正常、畅通。通过采用Gaussian函数计算各输入分量属于各语言变量值模糊集合的隶属度函数。
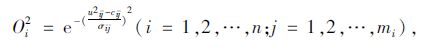
|
(8) |
式中,mi为xi的模糊分割数;cij为隶属度函数的中心,σij为隶属度函数的宽度;此层第k时刻的输入uij2(k)=Oi1(k)+Oij2(k-1)·θij,θij为递归神经的连接元。该神经网络动态映射的功能由此层中Oij2(k-1)记录网络k-1时刻的信息来完成。
第3层为规则层L3:通过计算出每个神经元代表模糊规则的适应度,来完成该层的语言变量输出。
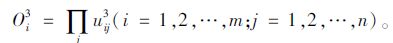
|
(9) |
第4层为标准化层L4:该层的节点数与上一层相同,实现数据的标准化、归一化处理。
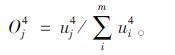
|
(10) |
第5层为输出层L5:对上一层每个模糊神经元的输出进行清晰化处理,最终得到清晰化量y。
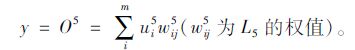
|
(11) |
入口匝道控制算法的参数训练方法采用的是遗传算法(Genetic Algorithms,简称GA)[16-17],GA是模拟生物进程中经遗传变异及适者生存达到物种进化的一种智能算法。算法经过个体选择、染色体交叉及变异等一系列遗传操作,从而解决复杂非线性、多极值问题,是一种强大的参数寻优方法。 GA的基本步骤:①通过编码和译码生成初始群体,并以该初始群体作为起点进行迭代搜索;②确定适应度函数以评估个体的优劣,表明个体的空间适应能力的强弱;③选择继承操作遵循达尔文优胜劣汰、适者生存的原则,个体适应度值越大的被选择保留以繁殖后代的机率就越多;④交叉操作经过随机选择交叉位置,产生新个体,并继承父代特性;⑤变异是在群体中随机选取个体,并通过一定概率随机其中的某值,但由于其如同生物界一样,变异的概率很抵,因此取值一般小于0.01,变异为产生新点提供机会。
选择算子是遗传算法最重要的算子之一,通过采用赌轮选择(Roulette wheel model)作为选择行为的选择策略。赌轮选择又称为适应度比例(Fitness proportion)选择,即各个体被选择的概率与个体对应的适应度值成正比:
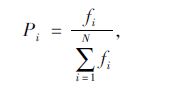
|
(12) |
式(12)中N为群体中个体的数量;fi为个体i的适应度函数。显然概率Pi反映的是个体在群体个体适应度总和中所占的比例,因此个体适应度越大,被选择的概率则越高。
通过遗传算法的进化过程,使种群朝全局最优方向收敛,以此实现对参数进行全局训练优化的目的。
2.4 基于GA的动态模糊神经网络学习算法首先用遗传算法对初始参数xρ(城市快速路交通流密度ρ)和xl(入口匝道排队长度l)进行调整优化,再通过BP算法实现加快入口匝道动态模糊神经网络控制算法的收敛速度。
定义目标函数,并使该函数的输出J达到最小:
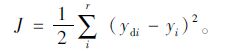
|
(13) |
函数式(13)中r为输出量个数;ydi为期望输出;yi为实际输出。
以下为遗传算法训练动态模糊神经网络的过程:
(1) 编码和译码。首先对初始参数x进行编码:若参数x的变化范围为[xmin,xmax],用L位二进制数b来表示,关系式为: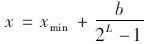
(2) 确定适应度函数: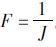
(3) 选择继承。对每个个体进行评价,将最大的适应度Fmax遗传给下一代。
(4) 交叉。对网络以概率值Pc(0.5~1.0)进行单点交互基因序列操作。
(5) 变异。以变异概率Pm(0.005~0.1)随机地改变个体的染色体基因,生成新个体。
完成遗传算法的训练后,则采用BP算法来完成入口匝道动态模糊神经网络的快速收敛。
令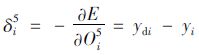

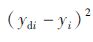
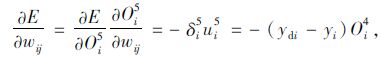
|
(14) |
再计算
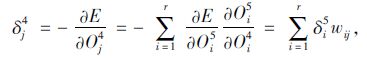
|
(15) |
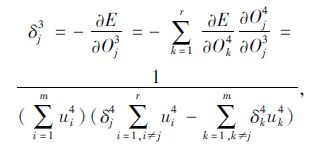
|
(16) |
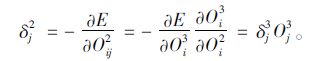
|
(17) |
因此,对于适应度函数的中心cij、宽度σij、和θij有:
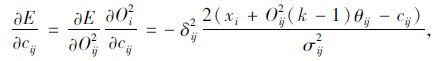
|
(18) |
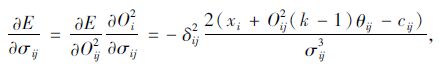
|
(19) |
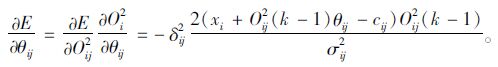
|
(20) |
最终得到参数调整的学习算法:(β>0为学习率)
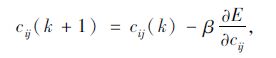
|
(22) |
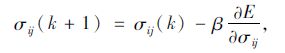
|
(23) |
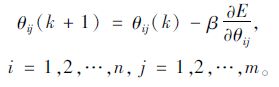
|
(24) |
通过MATLAB对设计的模型进行仿真试验:将实测数据输入到模型中,通过模糊化层计算输入分量的隶属度函数,并由该层的内部反馈连接调整相应参数、规则层,计算该模型神经元的适应度、标准化层,完成数据的标准化和归一化,最终的输出层对模型中的每个模糊神经元进行清晰化处理,并且仿真中采用遗传算法进行参数优化以改进该仿真模型。最后通过输出结果,验证算法对于入口匝道控制的有效性。
选取北京五环一段城市快速路对其进行仿真。这段城市快速路的入口匝道是2014年根据市政府“排堵保畅方案”要求新建的一条进入五环主路的匝道。该匝道建成初期,一定程度上改善该段区域内的交通环境,但近两年随着车辆的增多,该匝道进入主线的车辆对原城市快速路的通畅度造成了很大影响,入口匝道排队长度过长也使该区域呈辐射性的拥堵。
3.1 仿真参数基本设定根据到北京五环的快速路某路段的实地调查,入口匝道长度为150 m,主线的通行能力为2 300 veh/(km·lane),限速90 km/h;再通过实测数据,计算出该段城市快速路(选取的调查路段长1 km)临界密度ρ临和阻塞密度ρ阻分别为55 veh/(km·lane)和110 veh/(km·lane)。并在MATLAB的仿真开始时设定该段城市快速路的交通流密度ρ以及匝道排队长度l的模糊变量范围、交通流密度ρ以及匝道排队长度l的初始值,同时学习参数设为0.2,仿真的最小时间单位为10 s,总仿真步数1 000步。
3.2 仿真结果分析由实测数据得知,当上游交通量qu与入口匝道交通需求rd之和小于北京五环该路段的交通容量C时,快速路行驶通畅,此段快速路的交通流处于自由流状态,无法比较出不同控制模型的控制效果。因此仅对qu+rd≥C的情况进行仿真分析。
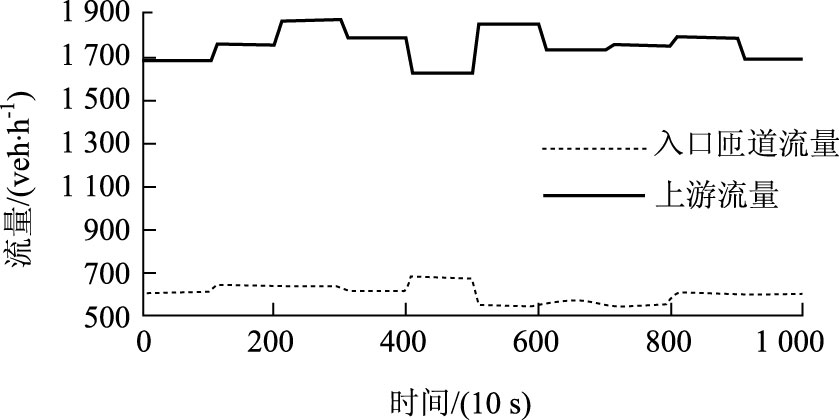
假设上游交通量qu和入口匝道交通需求rd的变化曲线如图 5所示。经过MATLAB工具仿真入口匝道无控制、经典ALINEA控制、动态模糊神经网络DFNN控制3种情况,得到的入口匝道调解率r变化曲线见图 6,主线交通流密度ρ曲线变化见图 7,入口排队长度l的曲线变化见图 8。
|
| 图 5 上游和入口匝道流量变化曲线 Fig. 5 Curves of upstream and on-ramp flows |
| |
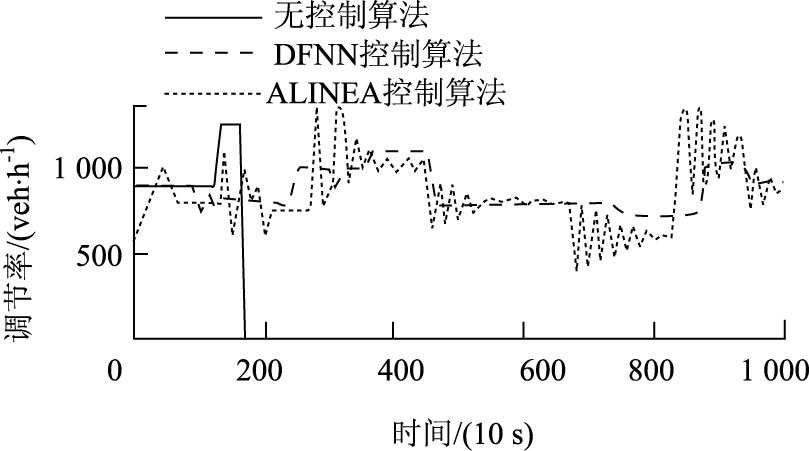
|
| 图 6 入口调节率曲线对比图 Fig. 6 Comparison of entrance regulation curves |
| |
由图 6可看出,没有入口匝道控制则在180步时入口匝道率骤降为0,不让匝道车辆进入快速路,同时还会造成回溢现象。经典的ALINEA则入口调解率振荡幅度大,不易于实现现实环境的入口匝道控制。反观动态模糊神经网络的入口匝道调解率曲线则平滑很多,有利于匝道放行信号控制器设计。
从图 7可看出,没有控制算法的城市快速路出现了严重交通堵塞的情况,而经典的ALINEA算法与动态模糊神经网络控制算法的控制效果则比较好,并且动态模糊神经网络控制算法能把主线的交通流密度控制在临界密度ρ临之内,经典的ALINEA算法则偶尔超出该临界范围外。
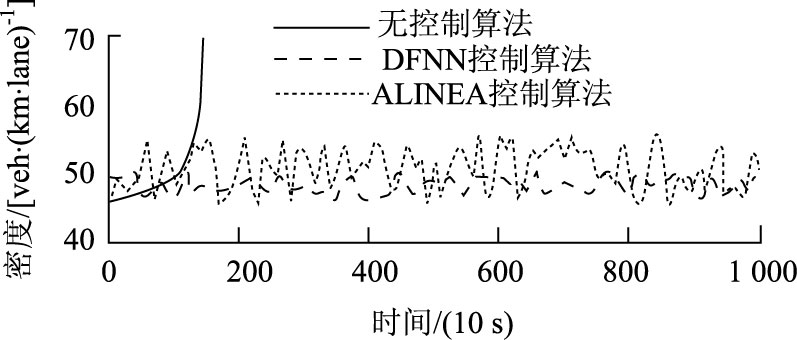
|
| 图 7 主线交通流密度曲线变化图 Fig. 7 Comparison of mainline traffic flow density curves |
| |
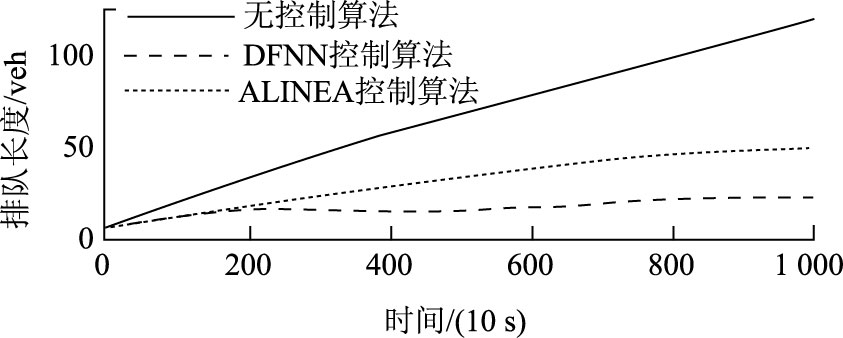
结合图 6~图 8可以看出,通过动态模糊神经网络控制算法得到的入口匝道调解率曲线和主线交通流密度曲线都相对平稳,波动不大,并且保证主线交通通畅的同时,对排队长度的控制效果也很好。
|
| 图 8 入口匝道排队长度曲线变化图 Fig. 8 Comparison of on-ramp queue length curves |
| |
通过仿真试验,验证了在入口匝道模糊神经网络控制算法内部引入递归环节,用遗传算法对网络进行训练的方法是有效的,使该算法能实时在线地对不断变化的交通状况做出合理的反应。
4 结论模糊神经网络是一种兼具鲁棒性强和自学习能力强的控制方法,本文在国内外学者将该方法应用于高速公路的智能控制领域的基础上,提出了动态模糊神经网络应用于城市快速路入口匝道控制的方法。并且该方法在规则模糊层引入了递归环节,在学习算法中引入遗传算法来调整优化初始参数,使之能随着城市快速路交通流特性能进行实时动态的自动调整控制策略,实现匝道的智能化控制。通过把多种智能控制算法结合起来应用于入口控制匝道系统中,利用各自的特点弥补单一控制算法的不足,将会是未来必然的趋势。
| [1] | 李俊辉, 黎新华, 谢小星. 基于概率神经网络的轨道交通车站客流安全状态评价[J]. 都市快轨交通, 2015, 28 (4) : 65-69 LI Jun-hui, LI Xin-hua, XIE Xiao-xing. Evaluation of Safety Status of Station Passengers in Urban Rail Transit Based on Probabilistic Neural Network[J]. Urban Rapid Rail Transit, 2015, 28 (4): 65-69 |
| [2] | 庞明宝, 任沙沙, 张晶晶. 基于混沌的高速公路主线速度模糊控制仿真[J]. 系统仿真学报, 2014, 26 (4) : 727-732 PANG Ming-bao, REN Sha-sha, ZHANG Jing-jing. Simulation on Variable Speed Limits of Freeway Mainline Based on Fuzzy Chaos Control[J]. Journal of System Simulation, 2014, 26 (4): 727-732 |
| [3] | 涂辉招, 孙立军, 高子翔. 基于风险评估技术的城市快速路多匝道协调控制时机研究[J]. 中国公路学报, 2015, 28 (7) : 86-92 TU Hui-zhao, SUN Li-jun, GAO Zi-xiang. Study on Control Timing of Coordinated Multi-ramp for Urban Freeway Corridors Based on Risk Assessment Technique[J]. China Journal of High and Transport, 2015, 28 (7): 86-92 |
| [4] | 陈金山, 郭建钢, 陆立峥, 等. 可变速度控制下快速路联动协同控制策略研究[J]. 华东交通大学学报, 2013, 30 (2) : 47-51 CHEN Jing-shan, GUO Jian-gang, LU Li-zheng, et al. Coordinated Linkage Control Strategy of Urban Expressway under Variable Speed Control[J]. Journal of East China Jiaotong University, 2013, 30 (2): 47-51 |
| [5] | SUMALEE A, ZHONG R X, PAN T L, et al. Stochastic Cell Transmission Model (SCTM):A Stochastic Dynamic Traffic Model for Traffic State Surveillance and Assignment[J]. Transportation Research Part B:Methodological, 2011, 45 (3): 507-533 |
| [6] | BARZINPOUR F, ESMAEILI V. A Multi-objective Relief Chain Location Distribution Model for Urban Disaster Management[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70 (5): 1291-1302 |
| [7] | AHMADI M, SEIFI A, TOOTOONI B. A Humanitarian Logistics Model for Disaster Relief Operation Considering Network Failure and Standard Relief Time:A Case Study on San Francisco District[J]. Transportation Research Part E:Logistics and Transportation Review, 2015, 75 (1): 145-163 |
| [8] | 陈晓玲. 基于模糊理论的高速公路智能控制系统探讨[J]. 工程建设与设计, 2016 (7) : 132-134 CHEN Xiao-ling. Study on Intelligent Control System of Expressway Based on Fuzzy Theory[J]. Construction & Design for Project, 2016 (7): 132-134 |
| [9] | 李胜琴, 杨春博. 车辆ESP模糊控制算法联合仿真研究[J]. 公路交通科技, 2013, 30 (10) : 147-151 LI Sheng-qin, YANG Chun-bo. Co-simulation of Fuzzy Control Algorithms for ESP on Vehicle[J]. Journal of Highway and Transportation Research and Development, 2013, 30 (10): 147-151 |
| [10] | 朱林波, 罗霞. 基于人工神经网络的微观交通仿真模型参数灵敏度分析[J]. 武汉理工大学学报:交通科学与工程版, 2014, 38 (2) : 426-429 ZHU Lin-bo, LUO Xia. Parameter Sensitivity Analysis of Microscopic Traffic Simulation Model Based on the BP Neural Network[J]. Journal of Wuhan University of Technology:Transportation Sciewe and Engineering, 2014, 38 (2): 426-429 |
| [11] | 李健, 贾元华, 敖谷昌. 主线机动容量合理分配的匝道协同控制[J]. 深圳大学学报:理学版, 2012, 29 (5) : 466-470 LI Jian, JIA Yuan-hua, AO Gu-chang. Reasonable Allocation of Flexible Capacity for Ramp Coordinated Metering[J]. Journey of Shenzhen University:Science and Engineering, 2012, 29 (5): 466-470 |
| [12] | PAPAMICHAIL I, KOTSIALOS A. Coordinated Ramp Metering for Freeway Networks:A Model-predictive Hierarchical Control Approach[J]. Transportation Research Part C:Emerging Technologies, 2010, 18 (3): 311-331 |
| [13] | BHOURI N, HAJ-SALEM H. Isolated Versus Coordinated Ramp Metering:Field evaluation Results of Travel Time Reliability and Traffic Impact[J]. Transportation Research Part C:Emerging Technologies, 2013, 28 (3): 155-167 |
| [14] | 胡彦梅, 封建湖, 陈建忠. 基于无振荡中心格式求解非均匀道路上的多车种LWR交通流模型[J]. 数学的实践与认识, 2015, 45 (4) : 18-24 HU Yan-mei, FENG Jian-hu, CHEN Jian-zhong. Non-oscillatory Central Scheme for a Multi-Class LWR Traffic Flow Model on an Inhomogeneous Highway[J]. Mathematics in Practice and Theory, 2015, 45 (4): 18-24 |
| [15] | CHUNG Y. Assessment of Non-recurrent Congestion Caused by Precipitation Using Archived Weather and Traffic Flow Data[J]. Transport Policy, 2012, 19 (1): 23-26 |
| [16] | 曲志坚, 张先伟, 曹雁锋, 等. 基于自适应机制的遗传算法研究[J]. 计算机应用研究, 2015 (11) : 3222-3225 QU Zhi-jian, ZHANG Xian-wei, CAO Yan-feng, et al. Research on Genetic Algorithm Based on Adaptive Mechanism[J]. Application Research of Computers, 2015 (11): 3222-3225 |
| [17] | 魏武, 张亚楠, 武林林. 基于遗传算法的改进AdaBoost算法在汽车识别中的应用[J]. 公路交通科技, 2010, 27 (2) : 114-118 WEI Wu, ZHANG Ya-nan, WU Lin-lin. Application of GA-based AdaBoost Algorithm in Vehicle Identification[J]. Journal of Highway and Transportation Research and Development, 2010, 27 (2): 114-118 |
 2017, Vol. 34
2017, Vol. 34

 ,
,