扩展功能
文章信息
- 李敏迪
- LI Min-di
- 车辆供给和距离效应对公共自行车借车行为影响
- Effect of Bike Supply and Distance Effect on Behavior of Borrowing Public Bikes
- 公路交通科技, 2017, 34(2): 121-128
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 121-128
- 10.3969/j.issn.1002-0268.2017.02.019
-
文章历史
- 收稿日期: 2016-06-14
公共自行车系统早在1950年便已存在,但并未规模化,直到2006年,巴黎率先成功运营后,才重新进入人们的视野。自行车共享世界地图网站()上的数据显示,直到2014年1月,全球50个国家712个城市拥有公共自行车系统,大约806 200辆自行车和37 500个车站投入运行。我国公共自行车系统于2008年在杭州市启动,并很快取得了成功。目前,公共自行车项目已在全国多个城市迅速扩展,正逐步形成我国未来公共交通系统的一种新模式。
随着我国社会经济的发展,由过量机动车带来的空气污染问题日益困扰人们的生活。公共自行车作为一种绿色、低碳的出行方式,有助于减少机动车购车需求。除了对环境的贡献,公共自行车系统还能有效地缓解城市交通拥堵问题。公共自行车具有小巧灵活、车速均衡的特点,是在高峰时段对低效的机动车一个很好的补充。另外,对于个人而言,公共自行车能有效解决“最后一公里”问题。
鉴于以上的诸多优点,公共自行车将成为我国城市公交一体化进程中一个不可或缺的重要环节。届时,其设计问题变得尤为重要。根据相关学术研究[1-29],本文认为公共自行车系统设计关键在于在不增加社会成本投入的情况下,尽可能增加人们的借车行为。而与借车行为最为相关的两个因素是自行车点位置分布与自行车供给,本文利用华盛顿哥伦比亚特区的历史数据对此问题进行研究,分析公共自行车系统中的车站位置分布距离效应(包括单个车站距离效应、车站间距离效应)与自行车供给(包括借车时自行车供给边际效应、还车时车位可得性情况)对出行者借车行为的影响程度,从而对我国公共自行车系统设计提出一些有用的建议。
1 文献综述 1.1 自行车点距离效应距离效应问题最初来源于交通系统设计中的可达到性问题。Allen等[30]将可达到性定义为在时间约束下一个人在空间中移动的能力。Murray等[31]强调了可达到性的物理属性,那便是人们的位置离交通点越近,人们使用此种交通方式的概率越大。Reilly[32]将物理领域牛顿提出的重力模型运用到了商业领域,他认为两地之间的距离越短,就会有更多的交易在二者之间产生。可以看出,已往学者通常从出行者角度(出行者到车站距离)或车站角度(车站间距离)对距离效应进行研究,并常常用车站间距离作为出行者到车站距离的替代,认为二者影响是等价的,鲜有将二者影响同时纳入分析。
1.2 自行车供给有关自行车供给,学术界研究最多的是出行者借车时自行车的可得性问题,即关注借车期间自行车存在与否对出借情况的影响,并将运营管理中的商品缺货概念引入公共自行车系统范畴。Ashish Kabra等[33]分别用自行车不可得时间段在总时间中的占比和高频时间段不同车站因缺少自行车供给导致出行者选择集合的变化来衡量自行车供给的长期影响和瞬时影响。而对自行车供给的研究却很少关注出行者还车时车位可得性问题。另外,除了可得性,自行车不同数量的供给带来的边际效应对借车行为的影响也鲜有人研究。
1.3 需求估计本文估计需求的方法与许多研究“备选集合”(Choice sets)的文献有关(Hauser 和Wernerfelt[34],Roberts 和 Lattin[35],Andrews和 Srinivasan[36])。这些研究关注对顾客考虑范围内的不同选择建立模型,从而估计顾客的偏好。在本文中,我们也遇到与之相似的问题,将具有可得性的不同车站看作是出行者的备选集合,需要估计每个出行者对不同车站的偏好。基于备选集合的模型是需求估计的重要工具,一般而言需要个体微观数据。但在实际研究中,微观数据一般很难收集,而加总数据则相对容易得到。如何在离散选择模型中使用加总数据,是长时间摆在研究者面前的一个现实问题。在经济学的文献中,大量的估计需求方法都是基于随机效用最大化模型(RUM)(Berry 1994[37])。RUM模型只需用到市场份额加总数据,对消费者偏好提供了一种非常有效的简化,大大减少了估计参数的数量。
2 研究设计 2.1 基本定义和假设本文从两个方面研究自行车出借行为受到的影响:车站位置分布距离效应和自行车供给。将车站位置分布距离效应定义为两种距离因素的总影响:第1种为单个车站距离因素,即为出行者到目标车站的步行距离;第2种为车站间距离因素,即为其他车站离目标车站的最近距离。亦从两个方面研究自行车供给的影响:一是借车时自行车供给边际效应,即不同数量自行车供给的影响程度;二是还车时车位可得性情况,即自行车供给影响下的车位是否可得情况。而对于借车时自行车可得性情况,Ashish Kabra等已做过细致研究,因此未将其纳入研究。根据研究需要,提出以下假设:
(1) 单个车站距离效应的减少会增加自行车借车行为。
用每个出行者到不同的自行车站所需要行走的距离,用来衡量单个车站的距离效应,此数据的采集需要获知每个出行者的起始位置,鉴于研究技术的限制,本文无法获取到相关数据,而解决此问题的方法是利用BLP模型对消费者离散选择模型进行加总,从而用加总数据替代微观数据进行参数估计。
(2) 车站间距离效应的减少会增加自行车借车行为。
其他车站距离目标车站最近的距离,用来衡量车站间的距离效应。
(3) 借车时自行车供给数量具有边际效应,数量每增加一单位时,其产生的效用递减。
对于自行车供给的研究,过去的文献将其纳入可得性问题研究,只是关注自行车是否可得对出借情况的影响,其中暗含着在自行车可得状态下,不同自行车数量对出借行为的影响是相同的假设。而本文认为,在现实中,自行车可得状态下不同数量的自行车供给对人们决策的影响是有差异的,即自行车供给存在边际效应。通常情况下,车站自行车供给量越高,使得人们更倾向于认为此车站更容易借到车,从而增加此车站借车次数,但当自行车供给量达到一定程度,人们对此因素的敏感度会随之下降,若继续增加自行车供给,并不会提高车站借车数量,增加的自行车便成为另一种形式的浪费。为了研究此差异性影响,本文用自行车供给率(每个车站可得自行车数量与总自行车数量的比例)来衡量自行车供给因素。
(4) 还车时车位可得性增加会增加自行车借车行为。
和自行车供给类似,车位供给本质上也是一个自行车可得性问题。过去的文献只考虑了借车时的可得性,而忽略了还车时的可得性。在华盛顿地区,人们常常因为自行车站没有车位而无法及时归还自行车,无论是临时更换还车点还是原地等待车位都会降低人们的效用,从而减少人们未来的借车行为,因此本文将车位供给因素纳入了模型,用车位供给率(车站有车位天数与总天数的比例)表示。由于出行者对于自行车归还到本车站还是其他车站敏感度并不同,本文将这两种情况分开考虑,分别用本车站车位供给率和其他车站车位供给率表示。
2.2 数据描述本文使用的数据来自于华盛顿哥伦比亚特区的Capital Bikeshare公共自行车系统。Capital Bikeshare 是美国最大的公共自行车项目,此系统覆盖了华盛顿市(哥伦比亚特区)和若干周边市镇,目前有329个运营点和超过5 000辆自行车,为当地居民提供24 h借车服务。本文对此公共自行车系统进行分析,选取了一个覆盖华盛顿哥伦比亚特区及周边市镇所有公共自行车点的矩形区域。对于区域内329个自行车站,选取了其中254个进行研究,由于其余75个车站年借车数量均低于100次,有充分理由认为这些车站因缺少维护等原因而未能正常运营,因而将其作为异常值从研究范围中删除。
采集目标区域内254个车站每15 min的自行车拥有数量,每次产生借车行为的时间、起始车站以及不同邮编地区的人口分布和密度数据,形成了3个数据集,数据的时间跨度是从2014年5月26日到2014年6月26日。华盛顿哥伦比亚特区的公共自行车系统建立于2010年9月,截至到本文的数据观测日,已经运营了4 a,因此有理由相信此系统在数据观测期间处于稳定运行状态,借车情况不会受到政府政策发布、人们关注度增加、车站布局改变等因素影响。数据观测期间处于春夏交界季节,天气宜人,降雨量小,有利于自行车出借,且此期间温度变化不大,可以减少天气突变对借车行为的影响。本研究去除了周末收集的数据,因为人们在周末的出行偏好与在工作日的出行偏好有很大的差异。另外,研究人们工作日的出行模式更有意义,因为在工作日高峰时间增加自行车出借数量对城市交通、空气质量的好处才是最大的。由于要研究每个出行者车站选择集合的动态变化情况,需要将3个数据集进行合并,合并后,数据最终包括44 724 784条观测。
2.3 模型建立首先建立离散的消费者选择模型,本研究需要估计的参数是出行者对于车站步行距离、车站间最近距离、自行车供给量、车位是否可得情况的偏好;然后利用BLP方法将离散数据进行加总,并将选择集合变化的动态性考虑进模型。
对于在人口密集分布的某一特定区域内,出行者i在t(t∈{1,…,T})时刻从公共自行车系统中的第f(f∈{1,…,F})个车站获得的效用可以表示为:

|
(1) |
式中,β0为截距;Li是出行者i的起始位置;d(Li,Lf)是出行者i与车站f(位于Lf)的距离;β1衡量出行者对于车站步行距离敏感度;本文将一天24 h划分成6个等时长的时间窗口,依次为:00~004 h,004~008 h,008~012 h,012~016 h,016~020 h,020~024 h,w表示t时刻所属的时间窗口;bikeratefw表示在时间窗口w中,车站f的自行车供给率,即时间窗口w内,车站f所有时点上可得的自行车数量总和与该时间窗口内该车站所有时点上全部自行车数量总和的比例;β2用来衡量其对出行者效用影响程度;dsrffw表示在时间窗口w中,车站f的本车站车位供给率,即时间窗口w内,车站f空车位大于3的天数占该时间窗口总天数的比例,因此β3用来衡量在车站f借车并在本车站归还车辆的出行者对于车位供给的敏感度;badffw是自行车供给率和本车站车位供给率的交互效应项,β4衡量其影响程度;dsrfw表示在时间窗口w中,车站f的其他车站车位供给率,因此,β5用来衡量在车站f借车并在其他车站归还车辆的出行者对于车位供给的敏感度。由于每个车站自行车归还目的地较多,本文选取了历史数据中归还数量最多的前5个车站作为其他车站的代表,将它们的dsrffw按照归还数量作为权数求均值,该均值即为dsrfw;fminf表示离车站f最近车站的距离,因此β6用来衡量车站网络化分布程度对出行者效用的影响;daffw表示dsrfw和fminf的交互效应,β7衡量其影响程度;γf,γw分别表示跟车站、时间窗口有关的固定影响因素;ξft表示在t时刻,未观测到的因素对车站f的所有出行者效用产生的共同影响。εft是基于出行者i、车站f、时间t的个别差异影响产生的误差项,假设这些误差项独立同分布。
出行者i也能使用其他类型的交通方式,在这种情况下他的效用为:
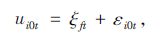
|
(2) |
式中,ξ0t表示在t时刻,未观测到的因素对所有选择其他交通方式的出行者效用的共同影响,假设此变量服从均值为0的正态分布;εi0t表示个别差异对选择其他交通方式效用的影响,仍然假设其独立同分布。
用Nt表示距离出行者500 m以内的车站集合,根据El-Geneidy等[25]研究,人们行走到附近交通系统距离的第85百分位大约是534 m,因此假设600 m 是人们可以接受最大的步行距离。用St表示在t时刻自行车可得的车站集合。那么对出行者i在t时刻的选择集合为Nt∩St。因此出行者i在t时刻使用车站f(f∈Nt∩St)里的自行车的概率为:
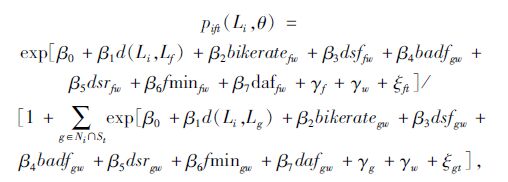
|
(3) |
式中,θ表示包括β0,β1,β2,β3,β4,β5,β6,β7,γf,γw在内的参数值;ξ.t表示在t时刻未观测因素的列向量。
用λft表示车站f在t时刻的借车次数,它由对观测区域内总人口的选择概率进行加总得到:
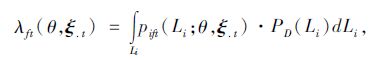
|
(4) |
式中,PD(Li)为潜在出行者初始位置的空间密度分布,本文假设此密度服从均匀分布。
值得注意的是,此模型将出行者选择集合的动态性考虑了进来。我们知道,缺少自行车的车站不能提供借车服务,而车站的自行车存在状况随着时间而不断变化,每一次时间更新,都需要将选择集合中自行车全部借出的车站剔除。本文模型建立在时间维度上,因此能够将不同时点上的选择集合进行更新,从而得到更加准确的估计。
2.4 模型估计本文模型估计方法建立在Ashish Kabra等改进的需求估计算法基础之上。由于Ashish Kabra等缺少各个车站发生借车行为的时间、位移数据,只能通过每2 min一次的车站状态变动量对借车行为次数进行估计,为了处理此大规模高频数据,Ashish Kabra等将状态相似的数据加总,将时间维度数据转化为状态维度数据,从而减小计算量。本文认为这样估计并不够准确,因为每2 min时间间隔内,车站既可能会产生借车行为也可能会产生还车行为,车站自行车数量减少量并不一定等于借车数量。本文与之不同的是,采集到各个车站发生借车行为的详细数据,从而能准确得到每个时间间隔产生的借车次数,再加上在华盛顿公共自行车系统中,出行者选择集合变动并不频繁,因此将车站状态时间间隔延长至15 min,不再需要进行数据加总就能够大大简化数据量,同时提高估计准确性。将所求的参数分为两部分:β1和其他参数,分别通过嵌套迭代对它们进行求解。嵌套过程的内迭代是在假设某β1值情况下,不断对其他参数进行更新,最终更新值与实际值收敛时,即为所求参数值。外迭代是用来搜索β1,当模型拟合效果最优时,即为所求β1。
用δft表示在效用模型中除β1的其他参数项:
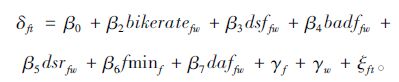
|
(5) |
对于∀f∈Ni∩St,出行者i的选择概率为:
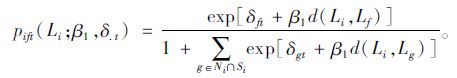
|
(6) |
车站f在t时刻的出借速率可以表示为:
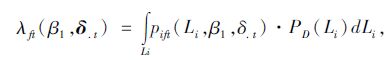
|
(7) |
式中,δ.t表示δft组成的列向量。首先对β1的值进行猜测,并对其赋值。然后在给定的β1情况下,假设一个δ.told的值,进行内循环的迭代:
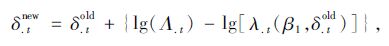
|
(8) |
式中,Λ.t是观测到的车站f在t时刻的实际出借速率。通过以上迭代,δ.tnew最终会收敛于δ.t的真实值。
值得注意的是,每次的迭代需要计算λ.t(β1,δ.t),根据式(7),这需要对不同空间密度函数下的所有出行者的出借速率加总。为了使此加总能够计算,将选定的目标区域分成边长为D米的正方形组成的网格,并且把每个正方形的中心看作是该范围内出行者的质点。因此,预计的出借次数可以表示为:
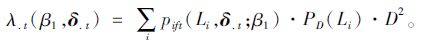
|
(9) |
使用式(9)能得到在给定的β1值下的δ.t,接下来利用式(5)来估计组成δ.t的参数。式(5)本质上是一个标准的回归模型,其中,bikeratefw,dsrffw,dsrfw,fminf是自变量;badffw,daffw为交互效应项。固定影响因素γf,γw是虚拟变量,ξft是误差项。至此完成了在给定β1下的内迭代参数估计过程。
对于外循环迭代,需要确定β1的值,使得模型整体拟合优度最小:
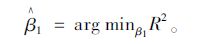
|
(10) |
用统计软件SAS实现对参数的估计,本文选取的外循环迭代精度为0.01,D为40 m。参数估计的结果和模型拟合程度如表 1、表 2所示。
| 变量 | 参数估计值 | 标准误差 | t值 | P值 |
| 截距 | 1.594 | 0.143 | 11.12 | <0.000 1 |
| d(Li,Lf) | -0.08 | — | — | — |
| bikerate | -2.272 | 0.155 | -14.58 | <0.000 1 |
| dsrf | -1.575 | 0.114 | -13.70 | <0.000 1 |
| badf | 2.597 | 0.152 | 17.04 | <0.000 1 |
| dsr | 0.269 | 0.048 | 5.58 | <0.000 1 |
| daf | -0.001 | 0 | -5.94 | <0.000 1 |
| fmin | -0.006 | 0 | -25.12 | <0.000 1 |
| 指标 | F统计量(P值) | R2 | 调整R2 | 变异系数 | 均方根误差 |
| 数值 | <0.000 1 | 0.799 | 0.799 | -42.024 | 1.101 |
根据参数估计的结果,初步可以得出以下结论:
(1) 车站步行距离的影响是负向且显著的,意味着出行者会对更远距离的车站产生显著的负效用。
(2) 车站自行车供给与本车站车位供给有程度较大且显著的交互效应,此交互效应与非交互项参数符号相反,表明在车位供给较大的情况下,出行者的效用会随着自行车供给增加而增加;在车位供给较小的情况下,出行者的效用会随着自行车供给增加而下降。这是因为,对于在本车站借车并在本车站归还的出行者来说,在车位比较充足的情况下,出行者更多关注的是借车时的自行车可得性,自行车历史供给越大,出行者会认为自行车越不容易出现借不到车的情况,从而增加其效用。而在车位比较满的情况下,出行者更多关注的是还车时的车位可得性,此时自行车历史供给越大,出行者会认为还车时更容易出现找不到空余停车位情况,从而减少出行者效用。
(3) 其他车站车位供给的影响为正向且显著,这说明,对于在本车站借车并在其他车站归还的出行者来说,增加目的地车站的车位供给会显著地增加他们的效用。
(4) 最近车站距离的影响为负向且显著,说明车站离其最近的车站距离越长,出行者在车站获得的效用随之减少。这意味着车站网络化分布程度越高,出行者效用也越高。
(5) 其他车站车位供给和车站网络化程度的交互效应为显著,且与车位供给参数符号相反,这说明在车站网络化程度较高的情况下,车位供给因素对出行者效用影响会更大。这不难理解,若出行者在一个“孤岛”车站借车并打算在其他车站归还,相较于“非孤岛”车站,他会在路途上花费更多的距离和时间;若目的地车站缺少停车位,出行者由此改变停车点多行车的距离相较其原本行车距离并不算大,因而车位供给因素对其负效用的影响会减少。
然而,以上从模型直接得到的参数估计仅描述了变量变动对出行者效用的影响,而本文最终想要探究的是这些因素对公共自行车系统出借行为的影响,这才更具有实际的意义。
首先,考虑车站步行距离对出借行为的影响。当所有出行者到所有车站步行距离均减少10%时,这可以等价于整个城市在保持原有车站网络结构不变的情况下,整体缩小10%。这样,目标区域面积减少19%(1-0.92),人口密度增加23.4%[1/(1-19%)-1]。将变化后的变量代入之前构建的出行者需求模型中(参数即为表 1估计值)重新计算,可以得到当步行距离减少10%后,目标区域内自行车出借数量的预测值,即为:
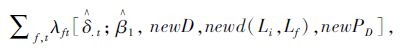
|
(11) |
式中,newD=90%D,newd(Li,Lf)=90% d(Li,Lf),newPD=1.234PD。经过计算发现,当步行距离减少10%后,会使得该系统中自行车出借数量增加2.9%。
其次,考虑自行车供给对出借行为的影响。当所有车站自行车供给均增加10%时,车站车位供给率也会相应减少,本文将变化后的变量带入需求模型中重新计算,可以得到当自行车供给增加10%后,目标区域内自行车出借数量的预测值,即为:
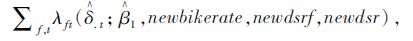
|
(12) |
式中,newbikerate=110%bikerate,newdsrf和newdsr是由newbikerate更新后计算得到。经过计算发现,当自行车供给增加10%后,会使得该系统中自行车出借数量仅增加0.28%。由此可知,在不增加车位的情况下增加自行车供给并不能使得系统中的出借数量显著增加。接下来考虑车位供给对系统中的出借数量变化情况,当所有车站车位供给新增10%时,目标区域内自行车出借数量的预测值为:
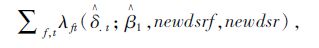
|
(13) |
式中,newdsrf=110%dsr,newdsr=110%dsr。经过计算发现,当车站车位供给率增加10%后,会使得该系统中自行车出借数量增加2.3%。
最后,考虑车站网络化分布程度对出借行为的影响。当所有车站离最近车站的距离减少10%时,目标区域内自行车出借数量的预测值为:
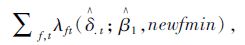
|
(14) |
式中,newfmin=90%。经过计算发现,当车站离最近车站的距离减少10%后,会使得该系统中自行车出借数量增加1%。
4 结论从以上分析可以看出,对于目前华盛顿哥伦比亚特区公共自行车系统来说,自行车供给和车站距离效应对其出借行为都有着显著的影响。其中,车站距离效应中,车站步行距离和车站间最小距离都对系统出借行为有着较大影响,因此在现有系统基础上增加车站分布的密度,能同时增加这两个因素的作用,因而对出借数量的增加是最有效率的;对于自行车供给,目前此系统中的借车者对还车时的可得性更加敏感,在现有系统中增加自行车供给数量并不能显著提高借车行为,而应该增加系统中自行车车位供给。对目前华盛顿哥伦比亚特区公共自行车系统设计提出的建议是:在保持自行车供给数量不变的情况下,应增加车站分布密度并且增加自行车车位供给。
目前,国内公共自行车系统还在建设阶段,未形成规模化,借车行为也不稳定,因此暂时无法得到有效的数据进行研究。但华盛顿哥伦比亚特区城市面积、体量和我国大、中型城市有相似之处。我国公共自行车系统在设计上应当采取自行车供给分散化策略,即在一定自行车供给数量下,尽量增加自行车站分布,加大距离效应。同时,不要一味增加车辆供给,而是应当注意车位与车辆之间数量的平衡。当然,国内出行者群体的选择偏好与华盛顿哥伦比亚特区居民有一定的区别,找出二者在借车行为上的具体差异,从而对国内公共自行车系统借车数量进行更加准确的预测,是未来研究的方向。
综上所述,本文在学术研究上有3点贡献。第一,本文提供了公共交通系统中出行者对自行车供给和车站距离效应反应的实证研究,此研究有助于改善现有公共自行车系统设计问题,提高自行车出借数量。第二,对于车站距离效应,过去文献将单个车站距离效应和车站间距离效应视为等价,而本文认为车站间距离反映了车站分布的网络化程度,出行者选择是否去车站借车不仅取决于与车站的绝对距离,还取决于与其他车站的相对距离,二者的影响是不同的,因此本文首次将两种距离效应分开研究。第三,对于自行车供给,本文做出两点创新:首先,对自行车供给数量进行分析,在过去文献仅研究可得性问题的基础上加入了对边际效应的分析;其次,过去文献仅考虑了借车时自行车可得性问题,本文首次将还车时车位可得性问题纳入研究范畴。
| [1] | FROEHLICH J, NEUMANN J, OLIVER N, et al. Sensing and Predicting the Pulse of the City through Shared Bicycling[C]//IJCAI'09 Proceedings of the 21st International Joint Conference on Artificial Intelligence. Pasadena:Morgan Kaufmann Publishers Inc., 2009:1420-1426. |
| [2] | VOGEL P, GREISER T, MATTFELD D C, et al. Understanding Bike-sharing Systems Using Data Mining:Exploring Activity Patterns[J]. Procedia Social and Behavioral Sciences, 2011, 20 (6): 514-523 |
| [3] | RAVIV T, KOLKA O. Optimal Inventory Management of a Bike-sharing Station[J]. ⅡE Transactions, 2013, 45 (10): 1077-1093 |
| [4] | BENCHIMOL M, BENCHIMOL P, CHAPPERT B, et al. Balancing the Stations of a Self Service "Bike Hire" System[J]. RAIRO-Operations Research, 2011, 45 (1): 37-61 |
| [5] | CHEMLA D, MEUNIER F, CALVO R W. Bike Sharing Systems:Solving the Static Rebalancing Problem[J]. Discrete Optimization, 2013, 10 (2): 120-146 |
| [6] | ROMERO J P, LBEAS A, MOURA J L, et al. A Simulation-optimization Approach to Design Efficient Systems of Bike-sharing[J]. Procedia-Social and Behavioral Sciences, 2012, 54 (4): 646-655 |
| [7] | BROACH J, GLIEBE J, DILL J. Development of a Multi-class Bicyclist Route Choice Model Using Revealed Preference Data[J]. International Conference on Travel Behavior Research, 2004, 50 (1): 15-33 |
| [8] | STINSON M A, BHAT C R. An Analysis of Commuter Bicyclist Route Choice Using a Stated Preference Survey[C]//TRB 2003 Annual Meeting.[S. l.]:TRB, 2003. |
| [9] | PARKIN J, ROTHERAM J. Design a Speeds and Acceleration Characteristics of Bicycle Traffic or Use in Planning, Design and Appraisal[J]. Transport Policy, 2010, 17 (5): 335-341 |
| [10] | SENER I N, ELURU N, BHAT C R. An Analysis of Bicycle Route Choice Preferences in Texas[J]. US. Transportation Research Board, 2009, 36 (5): 511-539 |
| [11] | DILL J, CARR T. Bicycle Commuting and Facilities in Major U.S. Cities:If You Build Them, Commuters Will Use Them[J]. Transportation, 200, 1828 : 116-123 |
| [12] | O'BRIEN O, CHESHIRE J, BATTY M. Mining Bicycle Sharing Data for Generating Insights into Sustainable Transport Systems[J]. Journal of Transport Geography, 2014, 34 (219): 262-273 |
| [13] | DEMAIO P. Bike-sharing:History, Impacts, Models of Provision, and Future[J]. Journal of Public Transportation, 2009, 12 (4): 41-56 |
| [14] | PADGHAM M. Human Movement is Both Diffusive and Directed[J]. Plos One, 2012, 7 (5): 37754-37754 |
| [15] | JENSEN P, ROUQUIER J B, OVTRACHT N, et al. Characterizing the Speed and Paths of Shared Bicycles in Lyon[J]. Transportation Research Part D:Transport and Environment, 2010, 15 (8): 522-524 |
| [16] | ANUPINDI R, DADA M, GUPTA S. Estimation of Consumer Demand with Stock-out Based Substitution:An Application to Vending Machine Products[J]. Marketing Science, 1998, 17 (4): 406-423 |
| [17] | BERRY S, PAKES A. Automobile Prices in Market Equilibrium[J]. Econometrica, 1995, 63 (63): 841-90 |
| [18] | DAVIS P. Spatial Competition in Retail Markets:Movie Theaters[J]. Rand Journal of Economics, 2006, 37 (4): 964-982 |
| [19] | HUFF D L. Defining and Estimating a Trading Area[J]. Journal of Marketing, 1964, 28 (28): 34-38 |
| [20] | LEDERMAN R, OLIVARES M, VAN RYZIN G. Identifying Competitors in Markets with Fixed Product Offerings[J]. Ssrn Electronic Journal, 2009, 12 (2): 202-219 |
| [21] | BROWN L N, GANS A, MANDELBAUM A, et al. Statistical Analysis of A Telephone Call Center:A Queueing-science Perspective[J]. Journal of the American Statistical Association, 2005, 100 (469): 36-50 |
| [22] | IBRAHIM R, WHITT W. Wait-time Predictors for Customer Service Systems with Time-varying Demand and Capacity[J]. Operations Research, 2011, 59 (5): 1106-1118 |
| [23] | ALLON G, FEDERGRUEN A, PIERSON M. How Much is a Reduction of Your Customers' Wait Worth? An Empirical Study of the Fast-Food Drive-Thru Industry Based on Structural Estimation Methods[J]. Manufacturing & Service Operations Management, 2011, 9 (4): 489-507 |
| [24] | MUSALEM A, OLIVARES M, BRADLOW E T, et al. Structural Estimation of the Effect of Out-of-stocks[J]. Management Science, 2010, 56 (7): 1180-1197 |
| [25] | EL-GENEIDY A, GRIMSRUD M, WASFI R, et al. New Evidence on Walking Distances to Transit Stops:Identifying Redundancies and Gaps using Variable Service Areas[J]. Transportation, 2014, 41 (1): 193-210 |
| [26] | ZHAO F, CHOW L F, LI M T, et al. Forecasting Transit Walk Accessibility:Regression Model Alternative to Buffer Method[J]. Transportation Research Record, 2003, 1835 : 34-41 |
| [27] | ALSHALALFAH B, SHALABY A. Case Study:Relationship of Walk Access Distance to Transit with Service, Travel, and Personal Characteristics[J]. Journal of Urban Planning & Development, 2007, 133 (2): 114-118 |
| [28] | AGRAWAL A W, SCHLOSSBERG M, IRVIN K, et al. How Far, By Which Route, and Why? A Spatial Analysis of Pedestrian Preference[J]. Journal of Urban Design, 2007, 13 (1): 81-98 |
| [29] | CRAIG C S, GHOSH A, MCLAFFERTY S. Models of the Retail Location Process:A Review[J]. Journal of Retailing, 1984, 60 (1): 5-36 |
| [30] | ALLEN W B, LIU D, SINGER S. Accessibility Measures of U.S. Metropolitan Areas[J]. Transportation Research Part B:Methodological, 1993, 27 (6): 439-449 |
| [31] | MURRAY A T, WU Xiao-lan. Accessibility Tradeoffs in Public Transit Planning. Journal of Geographical Systems[J]. Journal of Geographical Systems, 2003, 5 (1): 93-107 |
| [32] | CRAIG C S, GHOSH A, MCLAFFERTY S. Models of the Retail Location Process:A Review[J]. Journal of Retailing, 1984, 60 (1): 5-36 |
| [33] | KABRA A, BELAVINA E, GIROTRA K. Bike-Share Systems:Accessibility and Availability[R]. Chicago:The University of Chicago Booth School of Business, 2011. |
| [34] | HAUSER J R, WERNERFELT B. An Evaluation Cost Model of Consideration Sets[J]. Journal of Consumer Research, 1990, 16 (4): 393-408 |
| [35] | ROBERTS J H, LATTIN J M. Development and Testing of a Model of Consideration Set Composition[J]. Journal of Marketing Research, 1991, 28 (4): 429-440 |
| [36] | ANDREWS R L, SRINIVASAN T C. Studying Consideration Effects in Empirical Choice Models Using Scanner Panel Data[J]. Journal of Marketing Research, 1995, 32 (1): 30-41 |
| [37] | BERRY S T. Estimating Discrete-choice Models of Product Differentiation[J]. Rand Journal of Economics, 1994, 25 (2): 242-262 |
 2017, Vol. 34
2017, Vol. 34

