扩展功能
文章信息
- 陈秀锋, 曲腾姣, 田家斌
- CHEN Xiu-feng, QU Teng-jiao, TIAN Jia-bin
- 考虑不同出口转向的城市道路行程时间估计
- Estimation of Urban Road Travel Time Considering Different Exit Turning Movements
- 公路交通科技, 2017, 34(2): 93-99
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 93-99
- 10.3969/j.issn.1002-0268.2017.02.015
-
文章历史
- 收稿日期: 2016-03-29
行程时间是智能交通系统的主要参数之一,是衡量路网交通拥堵状况、出行效率的重要指标[1]。在城市路网中,行程时间是指从路段上游点到下游点所需时间的总和。由于城市道路交叉口信号控制、交通流自身的不守恒性,造成交叉口不同出口转向之间行程时间差别很大,准确估计城市路网行程时间仍然面临着挑战。
目前随着交通信息检测技术的多元化发展及数据融合技术的多样化,行程时间的短时预测通常将定点采集设备和移动采集设备进行多源数据融合[2]。基于固定检测器数据,可以分析交叉口延误对行程时间的影响,建立具有不同复杂程度的城市路网行程时间估计模型[3-7];移动采集设备通过采集浮动车行驶过程中的速度、位置、时间信息,获取车辆的行驶轨迹和行程时间数据[8-10];数据融合技术主要是对检测器和探测车数据进行融合,从而在多传感器数据资源中得到更准确全面的信息[11-13]。但是目前对行程时间的研究,大部分都是利用平均行程时间估计路网交通状态,忽略了因交通早晚高峰、商业住宅区及道路施工等各种因素引起的交通流转向分配不均匀、行程时间不具有代表性等问题。
因此,本文对城市路网行程时间进行研究时,考虑不同出口转向行车延误不同,需要的行程时间不同,因此以检测器和探测车获取的车辆通过断面数据为基础,估计城市路段不同出口转向的行程时间,通过对其进行试验分析,进一步验证方法的有效性和适用性。
1 行程时间分析 1.1 行程时间特性城市道路含有大量交叉口,每个交叉口存在不同的出口转向,因此两个连续信号控制交叉口之间路段的流量是指从上游不同进口车道到下游不同出口车道的汇入交通流量,如图 1所示。可以看出,从上游路口行驶至下游路口的车辆具有不同的路径选择,如O1→L,O3→S等,由于各种情况下车辆在交叉口之间的运行延误不同,所以每种组合形式下车辆运行所需行程时间也会有所不同。

|
| 图 1 交叉口不同出口转向示意图 Fig. 1 Traffic flow turning movements to different directions at intersection |
| |
图 2为某信号控制路段在某时间间隔内车辆到达下游交叉口时进行不同出口转向选择时所需的行程时间。可以看出,在该时间间隔内从上游点进行左转的车辆所需的行程时间远高于从上游点直行车辆的行程时间,从上游到下游的平均行程时间与各出口转向的行程时间均不相同。由此可见,对于具有不同出口转向选择的路段来说,以路段平均行程时间进行路网整体交通状态判别,容易忽略由交叉口局部拥堵演变成整个路网瘫痪的现象[14-15],因此有必要结合具体路段对不同出口转向的行程时间进行分析。

|
| 图 2 交叉口不同出口转向实际行程时间 Fig. 2 Real travel time of different exit turning movements from an intersection |
| |
1.2 行程时间的累积直方图模型
本文所提出的行程时间累积直方图是指在特定时间间隔内通过某道路断面的累积车辆数,其横坐标是时间,纵坐标是该时刻道路断面的累积车辆数,如图 3所示。

|
| 图 3 行程时间计算示意图 Fig. 3 Schematic diagram of calculating travel time |
| |
利用上游点和下游点的累积车辆数曲线U(t)和D(t)对行程时间进行分析,图中t1-t2时间段内通过上游断面的累计车辆数为U(t),t3-t4时间段内通过下游断面的累计车辆数为D(t), 则直方图曲线之间的面积S就是全部行程时间。运用反函数计算单位时间间隔(t1-t2或t3-t4)内的平均行程时间T为:
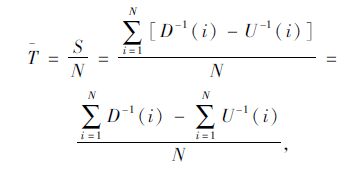
|
(1) |

|
(2) |
式中,N为时间t1-t2或t3-t4内到达上游点(离开下游点)的累积车辆数;U(t)为经过上游点的全部累积车辆数;U(t1),U(t2)分别为t1,t2时刻经过上游点的累积车辆数;D(i)为时刻i经过下游点的累积车辆数;D(t3),D(t4)分别为t3,t4时刻经过下游点的累积车辆数。
然而,在实际城市路网中,由于交叉口之间路段存在车辆的流入、流出以及检测器计数误差等,造成U(t)和D(t)计数存在相对偏差,从而影响行程时间的计算精度。为减少相对偏差对计算结果的影响,本文将累积直方图数据与探测车检测到的数据相融合,运用改进的累积直方图方法对下游点不同出口转向的平均行程时间进行计算。
2 出口转向行程时间累积直方图模型出口转向行程时间的累积直方图模型中,在原有累积直方图模型基础上,将U(t)替换为新的变量Um (t), 建立基于不同出口转向的行程时间模型。为了便于讨论,用字母m表示车辆不同的出口转向S,L,R,其中S表示直行,L表示左转,R表示右转,如图 1所示。则Um(t)和Dm(t)分别表示上游和下游m出口转向的累积车辆数。
那么图 1中O1,O2,O3 3个方向在上游路段的全部累积车辆数UA(t)的计算式为:

|
(3) |
式中,UA(t)为上游路段全部累计车辆数;Um(t)为m出口转向的上游累计车辆数;ε为误差参数。
如图 1所示,检测器布设在停车线处,则由检测器数据可求出Dm(t)和UA(t),但Um(t)是未知的,可以通过整合UA(t),Dm(t)和探测车数据对Um(t)进行估算,具体步骤如下:
(1) 计算UA(t)和Dm(t);
(2) 垂直缩放UA(t),对Um(t)进行初步估计;
(3) 利用探测车数据,重新计算Um(t);
(4) 将重新计算得出的Um′ (t)和Dm(t)代入式(10)中,估计路段具体出口转向的平均行程时间。
2.1 Um(t)初步估计定义变量Vm,p为有效比例因子,表示一天中p时间间隔内m出口转向的比例因子;ts,p和te,p分别表示p时间间隔车辆行程的起点和终点时间。本文Vm,p的取值可根据路段各出口转向的流量比例来设置各出口转向对应的比例因子值。
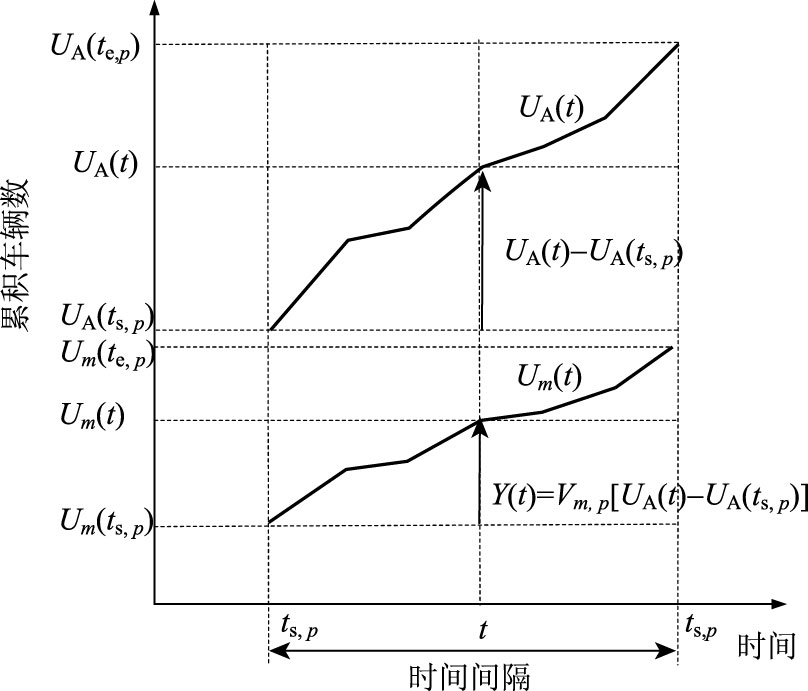
在p时间间隔的起始时刻ts,p对上游m出口转向的初始累积车辆数Um(ts,p)进行估计,然后运用式(4)对各时间间隔UA(t)以相应比例因子进行垂直缩放,如图 4所示,得出Um(t)的初始估计值。

|
(4) |
式中,Y(t)为ts,p到t时间间隔内进行m转向的车辆数;UA(t)-UA(ts,p)为ts,p到t时间间隔内的累积车辆数;Um(t)为t时刻进行m转向的累积车辆数。
|
| 图 4 垂直缩放UA(t) Fig. 4 Vertical scaling of UA(t) |
| |
2.2 融合探测车数据重新估算Um(t)
引入探测车的目的是为了使其在交叉口提供时间标记。本文将探测车采集到的数据定义为Dm(t)。假定有n辆探测车,探测车位于上游和下游的时间点分别为tu和td,首先需要对Um(t)曲线所经过的点进行定义,步骤如下:
(1) 将td的数据列表按照数据值的升序(即到达的先后顺序)进行排序。本文将探测车采集的下游不同出口转向数据作为Dm(t),因此需要按照Dm(t)的顺序对探测车到达的顺序进行定义。
(2) 将tu的数据列表按照数据值的升序(即出发的先后顺序)进行排序,以确保重新定义的 U′m (t)与Dm(t)是相互对应的。
(3) 将Um(t)经过的点定义为(tuj,D(tdj)),如图 5所示。其中tuj和tdj分别是tu,td数据列表中探测车j的数据。

|
| 图 5 融合探测车数据后重新计算Um(t) Fig. 5 Recalculating Um(t) with integrated probe data |
| |
Um(t)和Dm(t)最初是两个相互独立的累积直方图。当道路上车流量较少处于自由流状态时,将累积直方图数据进行初始化处理,定义初始参考点P0(U′m(t0)=Dm(t0))=0。选取道路上交通流量从自由流逐渐向缓行状态过渡的时刻作为tr,定义(Prtr,U′m(tr))为累积直方图中的一个参考点,在该点时刻原有累积直方图曲线Um(t)和重新定义的累积直方图曲线 U′m(t)共同经过该点。在绘制新的曲线U′m(t)时,需要先求出曲线所经过点(tp ,Yp)的表达式,(tp ,Yp)的计算式如式(5)~(7)所示:

|
(5) |

|
(6) |

|
(7) |
式中,U′m(t)为重新计算Um(t)得到的m出口转向的上游累积车辆数;Um(tr)为参考点Pr在tr时刻m出口转向的上游累积车辆数;Um(tp)为任意时刻tp进行m出口转向的上游累积车辆数;Yp为累积直方图模型中U′m(t)所经过点的累积车辆数;C为修正变量;s为缩放因子。
如图 5所示,在时刻tr之前不对原有直方图进行缩放,在tr-tp时间间隔对直方图进行垂直缩放,超过tp之后由于修正变量C为定值,对其进行垂直转换,从而使得U′m(t)是连续的,且在时刻tp平行于原有Um(t)。 最后利用U′m(t)与Dm(t)计算考虑出口转向的城市路段行程时间平均行程时间。
另外,式(4)中所运用的比例因子Vm,p,是将前一天各固定时间间隔的U′m(t)和UA(t)进行整合,用于对未来时刻路网交通状态进行预测,Vm,p的计算式如下:
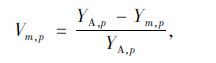
|
(8) |

|
(9) |
式中,te,p和ts,p分别为p时间间隔开始和结束时刻;YA,p和Ym,p分别为UA(t)和U′m(t)在p时间间隔内的累积计数;UA(te,p)和UA(ts,p)分别为te,p,ts,p时刻上游全部累积车辆数;U′m(te,p)和U′m(ts,p)分别为改进模型te,p,ts,p时刻上游m转向累积车辆数。
2.3 出口转向行程时间模型将上述计算过程得出的U′m(t)和检测器数据Dm(t)代入式(10)中,用于计算路段具体出口转向的平均行程时间Tm。
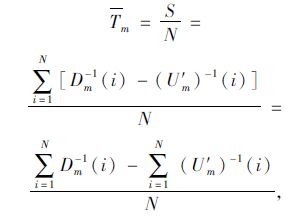
|
(10) |

|
(11) |
式中,Dm(i)为时刻i下游m出口转向累积车辆数;U′m (i) 为时刻i重新计算得出的上游m出口转向累计车辆数;U′m(t1)和U′m(t2)分别为t1,t2时刻上游m出口转向累计车辆数;Dm(t3)和Dm(t4)分别为t3,t4时刻下游m出口转向累积车辆数。
3 实例分析本文以黄岛开发区香江路从江山南路至武夷山路路段作为研究区域,该目标路段全长约2.1 km,包含5个交叉口,各交叉口之间路段距离分别为676,524,400,500 m。作为城市东西向主干道之一,进入路段的车辆大多为小汽车和客车,路段交通流量较大,研究区域及交叉口分布如图 6~图 7所示。

|
| 图 6 路段交叉口示意图 Fig. 6 Schematic diagram of road intersections |
| |

|
| 图 7 研究区域 Fig. 7 Study area |
| |
在运用改进后的累积直方图模型对整条路段的行程时间进行计算时,关键是需要对路段的计算单元进行划分。如图 6所示,基于交叉口数量的不同,可有两种划分方式。
第1种如图中①所示,将相邻两个连续信号控制的上下游交叉口组成研究单元,各研究单元之间相对独立,通过分析每个单元中上游和下游这一对累积直方图对各个分区单元的行程时间进行计算,最后整条路线的行程时间为各个单元行程时间之和。
第2种划分方式如图中②所示,是将一整条路段作为一个单元进行行程时间的计算,此时只需考虑起始交叉口。按照第①种方法进行计算时准确率相对较高,计算结果也更加符合实际情况,但存在计算量大、计算相对复杂的缺点。按照第②种方法计算也存在浮动车样本量不足的缺点,但是图 14则可以很好地证明虽然第2种划分方法的准确率比第1种方法低,但准确率相对较高,可以满足实际需求,因此本文选取第2种方法,即将一整条路段作为一个单元进行行程时间计算。
为了验证该计算方法的有效性,将神经网络模型作为对比模型,采用地磁检测器和视频检测设备采集的数据,利用开发区香江路2015年7月20日9:00—10:30的数据,分别测试神经网络模型和改进后的累积直方图模型从B点到L,S,R进行左转、直行、右转车辆的行程时间,研究路段出口转向示意如图 7所示。
将视频检测器采集的时间数据定义为实际行程时间ta,作为神经网络和改进的累积直方图模型的对比数据;同时,将利用这两种模型计算得出的出口转向行程时间定义为预测行程时间te,效果评价指标如下:

|
(12) |

|
(13) |

|
(14) |
式中,APEi为第i辆车行程时间绝对百分率误差;tai为第i辆车的实际行程时间;tei为第i辆车的预测行程时间;MAPE为行程时间平均百分率误差;AM为行程时间估计有效性百分率。
利用式(12)~(14)对路段运用上述两种模型进行左转、直行、右转3个方向行程时间的误差分析,结果如图 8~图 13所示,可以发现:

|
| 图 8 左转行程时间 Fig. 8 Travel time of turning left |
| |

|
| 图 9 左转行程时间误差分析 Fig. 9 Analysis of travel time error of turning left |
| |

|
| 图 10 直行行程时间 Fig. 10 Travel time of keeping straight movement |
| |

|
| 图 11 直行行程时间误差分析 Fig. 11 Analysis of travel time error of straight movement |
| |
|
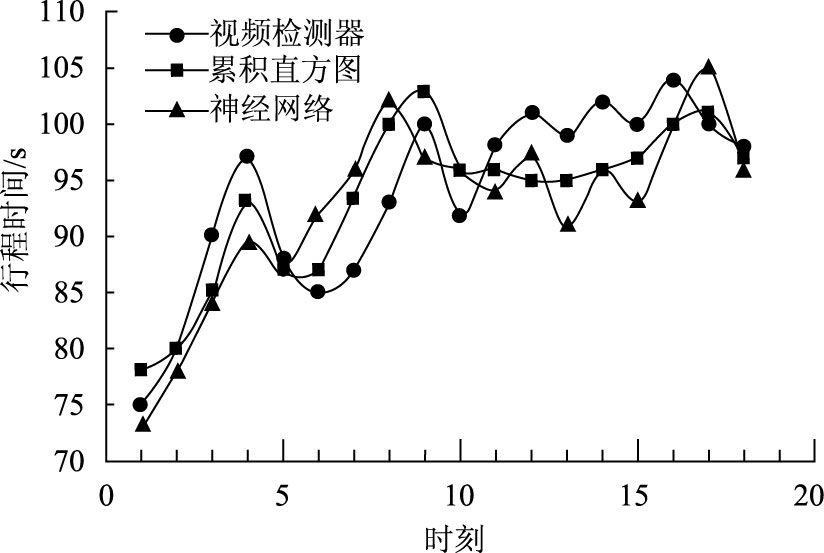
| 图 12 右转行程时间 Fig. 12 Travel time of turning right |
| |

|
| 图 13 右转行程时间误差分析 Fig. 13 Analysis of travel time error of turning right |
| |
(1) 从图 8、图 10、图 12行程时间预测结果可以看出,运用神经网络模型和累积直方图模型估计各出口转向行程时间与实际视频检测设备采集的行程时间相比虽存在一定差别,但总体上差别不大,且与神经网络模型的估算曲线相比,显然本文提出的累积直方图模型与实际数据更加接近,从神经网络模型的合理性可推断运用本文提出的累积直方图方法计算出口转向行程时间是合理的。
(2) 从图 9、图 11、图 13误差分析可知,虽然各个时刻两种方法的误差不尽相同,但从误差平均值可以看出,运用累积直方图方法进行行程时间预测误差总体上低于神经网络模型,准确度相对较高,且模型的整体误差通常控制在10%以内,能够较准确地对行程时间进行预测。
另外,改进后的累积直方图模型在计算过程中融合了检测器数据与探测车数据进行行程时间估计,但探测车作为移动数据采集技术本来就可提供行程时间数据,因此为评价这两种方法对行程时间估计的准确性,利用式(12)~(14),在探测车数量相同的前提下,对单位时间间隔内累积直方图模型和纯探测车对行程时间估计的百分率误差进行分析,结果如图 14所示,可以发现:

|
| 图 14 两种方法准确性对比图 Fig. 14 Comparison of accuracies of 2 models |
| |
(1) 采用累积直方图模型进行道路行程时间估计时,虽然前期探测车采集的数据较少时预测精度有所降低,但随着单位时间间隔内探测车数量的增加,估计精度明显提高,且运用该方法进行行程时间估计时,其平均精度能达到90%左右。
(2) 当单位时间间隔内通过预测路段的探测车数量较少时,本文所提出方法可通过融合检测器数据得出相对准确的数据,但采用纯探测车方法只有单位时间间隔内探测车数量较多时,其检测精度才会相应提高,且在每个估计周期内存在大量探测车的可能性较少,这也表明本文对多源数据进行融合处理的必要性。
4 结论现有行程时间估计模型的主要局限性表现为忽略了不同出口转向时交通运行状况的差异性,运用整个路段的平均行程时间对道路交通状态进行判别,在实际应用中容易产生由交叉口局部拥堵造成整个路网瘫痪的现象。因此,本文提出了基于改进的累积直方图模型的交叉口不同出口转向的行程时间计算方法。该方法通过融合检测器数据及探测车数据,能够使预测精度达到90%左右,并且相对于纯探测车方法。改进后的累积直方图模型对探测车数量的要求较低,能够简单有效地判断路口各方向是否处于交通饱和状态,对后续控制策略的制订及防止交通拥挤的加剧具有较高的应用价值。
但本文实例验证所采用的路段具有有效的探测车数据,对于其他没有探测数据或数据不可用的路段具有一定局限性,这是今后需要继续研究的内容。
| [1] | 李朝. 基于统计模型的城市道路交通旅行时间分析及预测方法研究[D]. 北京:北方工业大学,2015. LI Chao. Analysis on and Prediction of Travel Time on Urban Road Based on Statistic Model[D]. Beijing:North China University of Technology,2015. |
| [2] | 李瑞敏, 陈熙怡. 多源数据融合的道路旅行时间估计方法研究[J]. 公路交通科技, 2014, 31 (2) : 99-103 LI Rui-min, CHEN Xi-yi. Study on Methods of Travel Time Estimation Based on Multi-source Data Fusion[J]. Journal of Highway and Transportation Research and Development, 2014, 31 (2): 99-103 |
| [3] | AKCELIK R, ROUPHAIL N M. Overflow Queues and Delays with Random and Platooned Arrivals at Signalized Intersections[J]. Journal of Advanced Transportation, 1994, 28 (3): 227-251 |
| [4] | ZHANG H M. Link-journey-speed Model for Arterial Traffic[J]. Transportation Research Record, 1999, 1676 : 109-115 |
| [5] | ROBINSON S, POLAK J. Modeling Urban Link Travel Time with Inductive Loop Detector Data by Using the k-NN Method[J]. Transportation Research Record, 2005, 1935 : 47-56 |
| [6] | LIU H,VAN ZUYLEN H J,VAN LINT H, et al. Prediction of Urban Travel Times with Intersection Delays[C]//IEEE Conference on Intelligent Transportation Systems. Vienna:IEEE,2005:1062-1067. |
| [7] | YILDIRIMOGLU M, GEROLINIMIS N. Experienced Travel Time Prediction for Congested Freeways[J]. Transportation Research Part B:Methodological, 2013, 53 (4): 45-63 |
| [8] | ZHENG F, ZUYLEN H V. Urban Link Travel Time Estimation Based on Sparse Probe Vehicle Data[J]. Transportation Research Part C:Emerging Technologies, 2013, 31 : 145-157 |
| [9] | HELLINGA B R, FU L. Reducing Bias in Probe-based Arterial Link Travel Time Estimates[J]. Transportation Research Part C:Emerging Technologies, 2002, 10 (4): 257-273 |
| [10] | 朱爱华. 基于浮动车数据的路段行程时间预测研究[D]. 北京:北京交通大学,2007. ZHU Ai-hua. Research on Link Travel Time Prediction Method Based on Data Collected by Floating Car[D]. Beijing:Beijing Jiaotong University,2007. |
| [11] | 张旭. 面向交通运行状态评价的多源异质交通流数据融合技术方法研究[D]. 北京:北京交通大学,2008. ZHANG Xu. Fusion of Multi-source Heterogeneous Traffic Flow Data for Assessment of Traffic Operational Conditions[D]. Beijing:Beijing Jiaotong University,2008. |
| [12] | 胡小文, 杨东援. 基于数据融合的路段行程时间估计[J]. 交通信息与安全, 2011, 29 (4) : 92-98 HU Xiao-wen, YANG Dong-yuan. Link Travel Time Estimation Based on Data Fusion[J]. Journal of Transport Information and Safety, 2011, 29 (4): 92-98 |
| [13] | 李嘉, 刘春华, 胡赛阳, 等. 基于交通数据融合技术的行程时间预测模型[J]. 湖南大学学报:自然科学版, 2014, 41 (1) : 33-38 LI Jia, LIU Chun-hua, HU Sai-yang, et al. A Travel Time Prediction Model Based on Traffic Data Fusion Technology[J]. Journal of Hunan University:Natural Sciences Edition, 2014, 41 (1): 33-38 |
| [14] | 刘静. 基于车牌分析的交通状态判别方法研究[D]. 北京:北方工业大学,2015. LIU Jing. Research on Traffic State Identification Method Based on License Plate Recognition Data[D]. Beijing:North China University of Technology,2015. |
| [15] | 杨聚芬. 基于实时数据的路网交通状态可靠性分析方法研究[D]. 长春:吉林大学,2015. YANG Ju-fen. Research on Analysis Method of Traffic State Reliability of Road Network Based on Real-time Data[D]. Changchun:Jilin University,2015. |
 2017, Vol. 34
2017, Vol. 34

 ,
,