扩展功能
文章信息
- 陈绪军, 戴木香, 朱晓娥
- CHEN Xu-jun, DAI Mu-xiang, ZHU Xiao-e
- BFRP布加固钢筋混凝土梁的变幅疲劳寿命试验研究
- Experimental Study on Variable Amplitude Fatigue Life of RC Beams Strengthened with BFRP
- 公路交通科技, 2017, 34(2): 75-80
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 75-80
- 10.3969/j.issn.1002-0268.2017.02.012
-
文章历史
- 收稿日期: 2016-03-21
公路桥梁、铁路桥梁及工业厂房吊车梁等结构,除承受静载作用外,主要承受重复荷载的作用。承受重复荷载的结构,常常在低于静载使用载荷的情况下发生疲劳破坏。国内外已有的FRP加固混凝土结构的疲劳试验几乎都是针对常幅疲劳开展的[1-3],但实际工程中动载作用下结构承受的不是幅值不变的等幅载荷,而是随机变幅载荷。尽管等幅载荷疲劳试验研究的意义重大,但为了较好地反映实际工程中FRP加固的混凝土结构疲劳工作状态,有必要开展变幅疲劳试验研究。
已有FRP加固混凝土结构的疲劳性能研究几乎都是针对CFRP, GFRP和AFRP开展的,且几乎都是常幅疲劳研究[4-5]。关于物理、力学性能优异的BFRP加固混凝土结构的变幅疲劳研究,国内外尚未见到他人研究成果[6]。因此,开展BFRP加固混凝土梁的疲劳性能研究,尤其是开展变幅疲劳研究是有意义的。
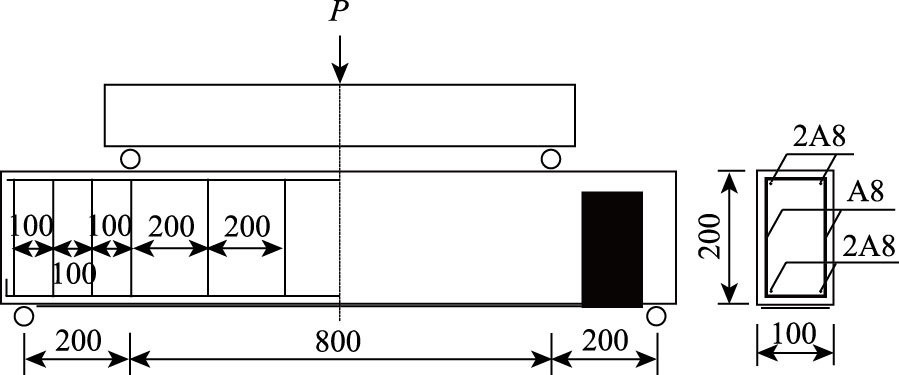
1 变幅疲劳试验研究 1.1 试验概况本文共设计5根试验梁,横截面尺寸均为100 mm×200 mm、计算跨度1 200 mm、剪跨200 mm,加载装置及加固方案分别见图 1和表 1。每根试验梁受拉纵筋跨中处粘贴电阻应变片,当疲劳循环次数N达到预定值时,停机卸载至零,然后再施加最大值等于疲劳荷载上限的静载,加载期间采用DH3816数据采集系统采集试验数据。
|
| 图 1 加载装置(单位:mm) Fig. 1 Loading set-up (unit:mm) |
| |
| 试件 编号 | 纤维布 类型 | 粘贴 层数 | 纤维布 长度/mm | 锚固 措施 | 破坏形式 |
| P0 | - | - | - | - | 纯弯段钢筋断裂 |
| PB1 | BFRP | 1 | 1 100 | 有 | 纯弯段钢筋断裂 |
| PB2 | BFRP | 2 | 1 100 | 有 | 纯弯段钢筋断裂 |
| PCB2 | CFRP+BFRP | 2 | 1 100 | 有 | 纯弯段钢筋断裂 |
| PCG2 | CFRP+GFRP | 2 | 1 100 | 有 | U型箍断裂 |
1.2 试验梁所采用材料
混凝土立方体抗压强度实测平均值为56.52 MPa;梁内纵筋、箍筋均采用直径为8 mm的光圆钢筋,梁顶与梁底纵筋各配置2根;箍筋双肢,在纯弯段内间距200 mm,剪跨段间距100 mm;钢筋屈服强度平均值为507.45 MPa,弹性模量为206.67 GPa。粘贴在梁底的纵向纤维布尺寸均为80 mm×1 100 mm,纵向纤维布的两端各设置一道U型箍锚固,纤维布的材料力学性能见表 2。
| 纤维布 类型 | 计算厚度/ mm | 抗拉强度/ MPa | 弹性模量/ GPa | 极限应变/ % |
| BFRP | 0.111 | 1 859.1 | 97.8 | 1.90 |
| CFRP | 0.167 | 4 325.5 | 299.4 | 1.40 |
| GFRP | 0.169 | 2 634.0 | 96.3 | 2.74 |
1.3 加载制度
施加疲劳荷载前,先预加载,预加载值约为疲劳荷载上限的70%,预载后施加静载,期间采集相关试验数据。疲劳试验加载频率为5 Hz,疲劳荷载下限为18 kN,当疲劳循环达到预定次数试验梁未疲劳破坏时,改变疲劳荷载上限值,继续疲劳试验,疲劳荷载幅值见表 3。在疲劳循环次数达到2,5,10,30,50,95,155,200,250,285,300万次时,停机卸载至零,再加静载,期间量测残余挠度和挠度,混凝土、钢筋和纤维布应变。
| 试件 编号 | 第1级荷载 幅疲劳次数 /万次 | 第2级荷载 幅疲劳次数 /万次 | 第3级荷载 幅疲劳次数 /万次 | 第4级荷载 幅疲劳次数 /万次 | 疲劳寿命/ 万次 |
| P0 | 78.335 | 0 | 0 | 0 | 78.335 |
| PB1 | 130.213 | 0 | 0 | 0 | 130.213 |
| PB2 | 200.000 | 50.000 | 13.035 | 0.000 | 263.035 |
| PCB2 | 200.000 | 50.000 | 30.000 | 11.260 | 291.260 |
| PCG2 | 200.000 | 50.000 | 30.000 | 18.630 | 298.630 |
| 注:第1级荷载幅为42 kN,疲劳荷载上限为60 kN;第2级荷载幅为57 kN,疲劳荷载上限为75 kN;第3级荷载幅为62 kN,疲劳荷载上限为80 kN;第4级荷载幅为77 kN,疲劳荷载上限为95 kN。 | |||||
2 试验结果分析 2.1 试验梁疲劳破坏形态及疲劳寿命
除PCG2梁发生的是U型箍断裂破坏外,其余试验梁的疲劳破坏均始于受拉纵筋的疲劳断裂。钢筋疲劳断裂的试验梁在未出现明显预兆的情况下,伴随着一声巨响,受拉区钢筋断裂的同时纵向纤维布断裂,整根梁断成两截,钢筋的断口处有明显的疲劳破坏特征,试验梁的破坏形态如图 2所示。梁的断裂破坏面几乎在梁的跨中处,而且断裂面几乎都发生在纯弯段内某条主裂缝所在截面处,一般主裂缝的位置为箍筋所处截面附近或钢筋应变片粘贴处截面附近。

|
| 图 2 试验梁破坏形态 Fig. 2 Failure modes of test beam |
| |
由表 3可见,未加固的对比试验梁的疲劳寿命只有78.335万次,而粘贴一层玄武岩纤维布后,试验梁的寿命显著提高到130.213万次,粘贴两层纤维布的试验梁,即使疲劳荷载上限历经75, 80, 95 kN提高后,其寿命相对粘贴一层纤维布加固梁仍大幅延长,延长幅度分别达到了135.78%,171.81%和181.22%。可见,实际工程中承受疲劳荷载的钢筋混凝土梁,粘贴玄武纤维布或混杂纤维布,能极大地改善梁的抗疲劳性能,能有效延缓梁的疲劳损伤累积,且纤维布粘贴层数越多,抗疲劳效果越明显,疲劳寿命延长越显著。
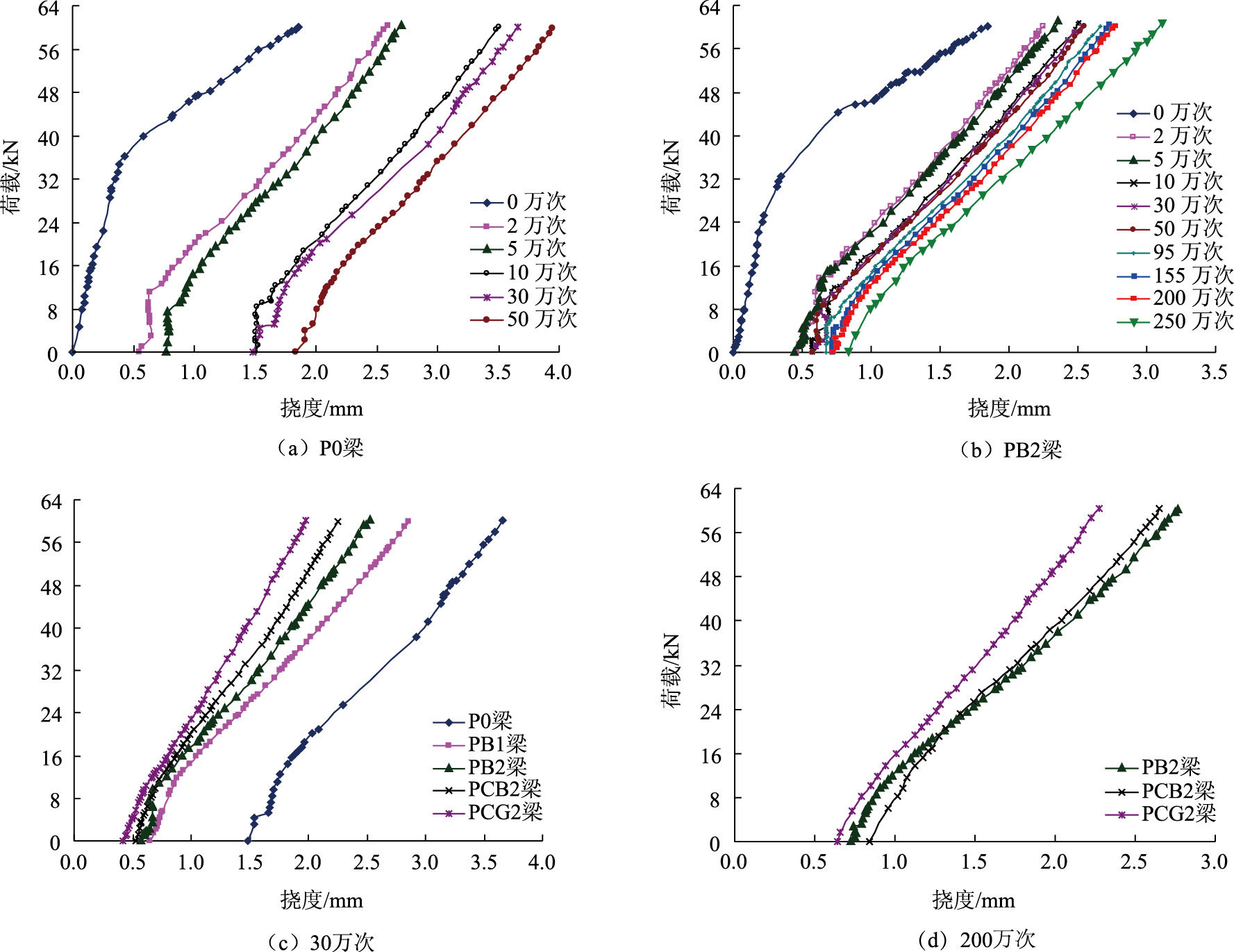
2.2 梁荷载-挠度分析图 3是试验梁跨中荷载-挠度曲线,由图 3(a)~图 3(b)可知,梁的挠度与疲劳荷载循环次数以及应力幅有着密切的关系。随疲劳荷载循环次数的增加,梁的挠度不断增大;疲劳荷载循环达到2万次时,未加固的P0梁和加固的PB2梁的挠度较0万次时均大幅增加,而且残余挠度均达到0.5 mm左右;10万次时,P0梁挠度和残余挠度仍增加明显,而PB2梁却不显著,加固的PB1,PCB2,PCG2各梁的荷载-挠度随疲劳荷载循环次数而改变的特征都与PB2梁类似。由图 3(b)可见,随疲劳荷载上限的提高,PB2梁的挠度曲线斜率减小,偏向挠度轴,其他加固梁亦如此。这是因为,疲劳荷载上限的提高使得应力幅增加,应力幅越大,相同疲劳循环次数下,梁的疲劳损伤越大。
|
| 图 3 荷载-挠度曲线 Fig. 3 Load-deflection curves |
| |
从图 3(c)和图 3(d)可以看到,疲劳循环次数相同时,梁的挠度随FRP粘贴层数的增多而减小。30万次时,未加固的P0梁残余挠度是加固梁的1.5倍左右,荷载越大,P0梁与PB1,PB2,PCB2,PCG2梁的挠度比值越大,FRP粘贴层数越多挠度比值也越大;粘贴层数相同时,梁的挠度随FRP的平均强度提高而较小,即挠度关系满足PCG2<PCB2<PB2。
以上表明,粘贴FRP布能有效改善梁的抗疲劳性能,减缓梁内部损伤累积,降低钢筋的塑性变形,延缓梁的刚度退化,起到很好的耗能效果。
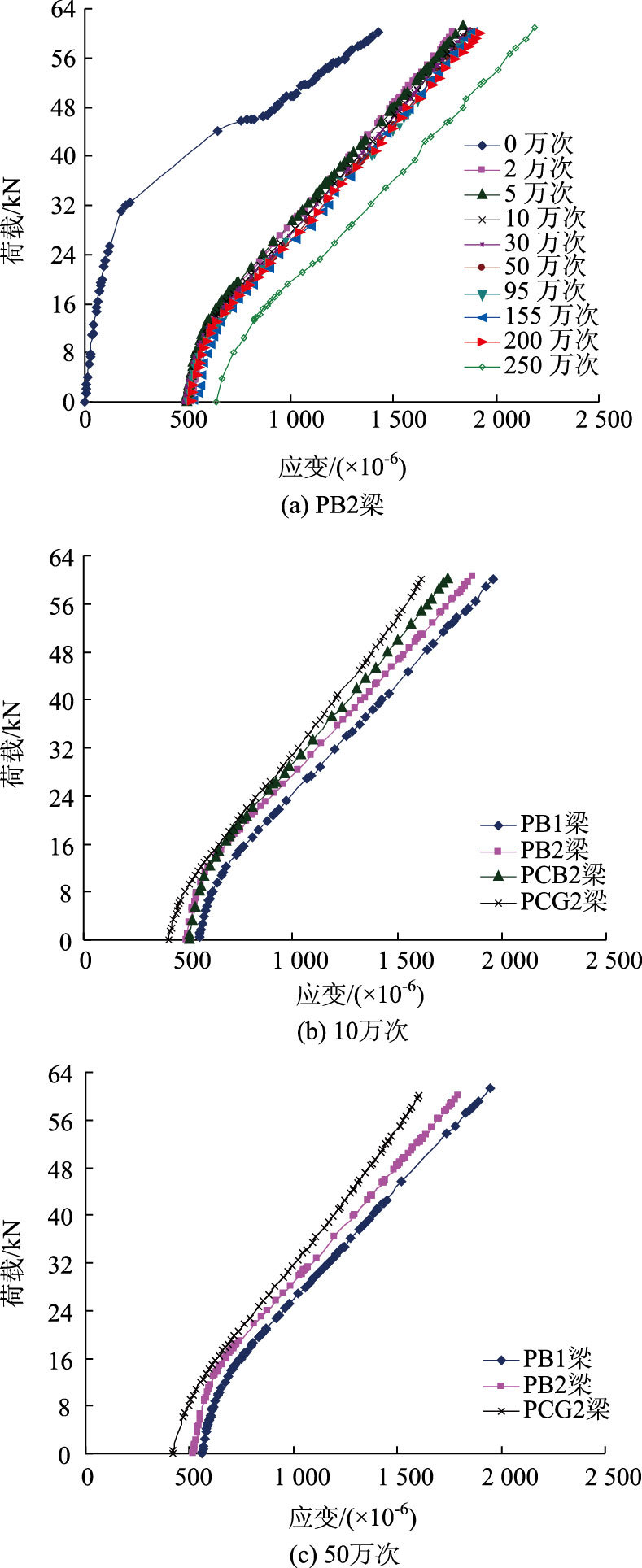
2.3 钢筋应变分析钢筋应变与疲劳循环次数、FRP粘贴层数的关系见图 4。由于应变片失效,未能采集到P0梁钢筋的应变值。由图 4可知,加固梁在整个寿命期内钢筋的荷载-应变曲线随疲劳荷载循环次数的变化关系,以及随FRP粘贴层数的变化关系与荷载-挠度曲线相类似。疲劳荷载循环初期,随疲劳循环次数的增加,PB2梁(其他加固梁与PB2梁类似)受拉钢筋的残余应变累积非常显著;疲劳循环2万次之后,随着荷载循环次数的增加,残余应变变化不如疲劳初期明显,应力幅不变时,钢筋荷载-应变曲线近乎平行。这说明,应力幅相同时,每一次疲劳循环产生的疲劳损伤是相等的,即疲劳损伤是按线性规律累积的。当疲劳荷载上限提高即应力幅增加,钢筋应变随疲劳循环次数增加而明显增大,且随应力幅增加,钢筋的荷载-应变曲线斜率明显减小,偏向应变轴,这表明随应力幅的增加,受拉钢筋每一次疲劳循环产生的疲劳损伤大于前一个应力幅每一次疲劳循环产生的疲劳损伤。
|
| 图 4 荷载-钢筋应变曲线 Fig. 4 Load-strain curves of steel bar |
| |
图 4(b)和图 4(c)表明,历经相同的疲劳循环次数,FRP布粘贴层数越多,钢筋的残余应变和应变越小。粘贴2层纤维布的PB2,PCB2,PCG2梁,残余应变大小不一,PB2>PCB2>PCG2,应变亦如此。可见,FRP布的平均强度越大,越能改善钢筋的疲劳受力性能,钢筋的疲劳损伤也越小,相同载荷幅下,梁的疲劳寿命也就越大。
3 变幅疲劳荷载下的疲劳寿命估算已有研究表明,无论是锚固措施可靠的FRP加固梁还是未加固的普通钢筋混凝土梁,其受弯疲劳破坏几乎都由受拉纵筋的疲劳断裂控制,因此FRP加固的钢筋混凝土梁,受拉纵筋的疲劳寿命即为试验梁的疲劳寿命。本文FRP加固的钢筋混凝土梁的疲劳寿命估算均是根据梁内受拉纵筋进行的。
对于变幅载荷作用下构件的疲劳寿命估算,疲劳损伤累积理论得到了学术界和工程界的肯定。到目前为止,已有几十种疲劳累积损伤理论被先后提出。但只有Miner损伤理论、修正Miner损伤理论、相对Miner损伤理论、Corten-Dolan损伤理论和Manson双线性损伤理论在实际工程中得到较多应用。相对Miner损伤理论精度虽然高,但在缺乏试件服役载荷下的累积损伤总和D的试验数据时无法应用;Manson双线性损伤理论计算过程复杂繁琐,且精度没有优势[7-8]。因此本文采用其他3种疲劳损伤累积理论来估算变幅疲劳载荷作用下FRP加固梁的抗弯疲劳寿命。
3.1 等幅疲劳下光圆钢筋的S-N曲线关于普通钢筋混凝土梁采用的光圆钢筋疲劳强度,国内外研究者进行了大量的试验研究。日本学者国分正胤基于配有光圆钢筋的混凝土梁疲劳试验,给出了埋置在混凝土中的光圆钢筋S-N曲线:
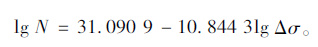
|
(1) |
曾志斌[9]基于光圆钢筋在空气中的疲劳试验,给出的光圆钢筋在空气中的疲劳S-N曲线见式(2),其认为对于埋在混凝土中的光圆钢筋,可以将式(2)的S-N曲线降低1/6使用。
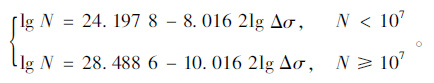
|
(2) |
Miner损伤理论认为,疲劳损伤是按照线性规律累积的,试件在k个应力幅σi作用下各经历ni次循环,则其损伤总和D为[10]:
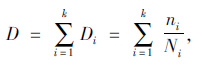
|
(3) |
式中,ni为试件在第i级应力幅σi作用下的疲劳循环次数,由荷载谱给出;Ni为试件在第i级应力幅σi作用下的常幅疲劳寿命,可通过S-N曲线求得。当损伤总和D=1时,认为构件发生疲劳破坏。
3.3 修正Miner损伤理论根据修正Miner损伤理论,当疲劳试件的损伤总和D为一个不等于1的常数a时,试件发生疲劳破坏[11],即:
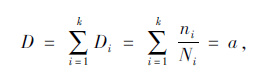
|
(4) |
式中a值由二级或三级变幅疲劳试验确定,其他参数意义参见式(3)。根据文献[7]中的表 2,本文取a=1.278。
3.4 Corten-Dolan损伤理论Corten-Dolan理论考虑了加载顺序对疲劳累积损伤的影响,认为高应力幅会加速低应力幅作用下的损伤,即高应力幅作用下,σi循环ni次所造成的损伤大于ni/Ni,其表达式见式(5)[12]。
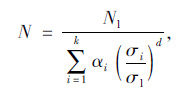
|
(5) |
式中,N为k级应力幅下试件的疲劳总寿命;σl为k级应力幅中最大的应力幅值;Nl为最大应力幅值σl作用下的常幅疲劳寿命;αi为应力幅σi作用下的循环次数占总循环次数的比例;d是与应力状态有关的材料常数,由二级载荷试验确定,根据文献[8],本文取d=4.8。
3.5 各种累积损伤理论疲劳寿命估算结果及比较根据以上3种损伤理论,分别对各试件的疲劳寿命进行了估算,结果详见表 4。将NT与NM代入式(3),可以看出损伤总和D值均大于1,这可能是因为:①本试验中每个载荷循环周期内平均应力均大于零,与Miner损伤理论的载荷必须是对称循环的假定不符;②本试验中加载次序为低→高的应力循环,使得钢筋产生了“锻炼”效应。根据Miner损伤理论估算出的试验梁疲劳寿命精度较修正Miner损伤理论偏低,较Corten-Dolan损伤理论偏高,且无论由哪种损伤理论得到的疲劳寿命估算值均偏安全,其中修正Miner损伤理论精度最好,故建议在实际工程应用中采用修正Miner损伤理论进行疲劳寿命的估算。
| 试件编号 | NT/万次 | NM/万次 | NMM/万次 | NC/万次 |
| PB2 | 263.035 | 182.974 | 218.250 | 100.399 |
| PCB2 | 291.260 | 210.331 | 250.783 | 197.202 |
| PCG2 | 298.630 | 217.250 | 262.915 | 213.954 |
| 注:(1)为试验梁的变幅疲劳寿命试验值。(2) NT,NM,NMM,NC分别为试验梁的实测寿命值和按Miner损伤理论、修正Miner损伤理论、Corten-Dolan损伤理论得到的变幅疲劳寿命估算值。 | ||||
4 结论
(1) 粘贴玄武岩纤维布对提高钢筋混凝土梁的抗弯疲劳寿命非常有效,粘贴两层纤维布使试验梁的寿命得到了极大延长。
(2) 对于FRP加固的钢筋混凝土梁,Miner损伤理论、修正Miner损伤理和Corten-Dolan损伤理论估算出的抗弯变幅疲劳寿命均偏安全。
(3) 3种损伤理论中,修正Miner损伤理论估算的疲劳寿命精度最高,建议在实际工程应用中采用修正Miner损伤理论进行疲劳寿命的估算。
| [1] | SHAHAWY M, BEITELMAN T E. Static and Fatigue Performance of RC Beams Strengthened with CFRP Laminates[J]. Journal of Structural Engineering, 1999, 125 (6): 613-621 |
| [2] | FERRIER E, BIGAUD D, CLEMENT J C, et al. Fatigue-loading Effect on RC Beams Strengthened with Externally Bonded FRP[J]. Construction and Building Materials, 2011, 25 (2): 539-546 |
| [3] | 邓宗才, 李凯. 预应力与非预应力AFRP加固腐蚀钢筋混凝土梁疲劳性能研究[J]. 土木工程学报, 2009, 42 (9) : 54-60 DENG Zong-cai, LI Kai. Experimental Study on Fatigue Performance Corroded Reinforced Concrete Beams Strengthened with Prestressed AFRP Sheets[J]. China Civil Engineering Journal, 2009, 42 (9): 54-60 |
| [4] | PAPAKONSTANTINOU C G, PETROU M F, HARRIES K A. Fatigue Behavior of RC Beams Strengthened with GFRP Sheets[J]. Journal of Composites for Construction, 2001, 3 (2): 246-253 |
| [5] | OUDAH F, EL-HACHA R. Analytical Fatigue Prediction Model of RC Beams Strengthened in Flexure Using Prestressed FRP Reinforcement[J]. Engineering Structures, 2013, 46 : 173-183 |
| [6] | 张海阔.玄武岩纤维布加固混凝土连续梁的疲劳与冻融耐久性研究[D].长春:吉林建筑大学, 2015. ZHANG Hai-kuo. Research of Basalt Fiber Sheet Reinforced Concrete Continuous Beam Fatigue and Freeze-thaw Durability[D].Changchun:Jilin Jianzhu University, 2015. |
| [7] | 赵少汴. 变幅载荷下的有限寿命疲劳设计方法和设计数据[J]. 机械设计, 2000 (1) : 5-8 ZHAO Shao-bian. Fatigue Design Methods and Design Data for Finite Life under Variable Amplitude Loading[J]. Journal of Machine Design, 2000 (1): 5-8 |
| [8] | 赵少汴. 常用累积损伤理论疲劳寿命估算精度的试验研究[J]. 机械强度, 2000, 22 (3) : 206-209 ZHAO Shao-bian. Study on the Accuracy of Fatigue Life Predictions by the Generally Used Damage Accmulation Theory[J]. Journal of Mechanical Strength, 2000, 22 (3): 206-209 |
| [9] | 曾志斌, 李之榕. 普通混凝土梁用钢筋的疲劳S-N曲线研究[J]. 土木工程学报, 1999, 32 (5) : 10-14 ZENG Zhi-bin, LI Zhi-rong. Research on Fatigue S-N Curves of Reinforcing Bars in Common Reinforced Concrete Beams[J]. China Civil Engineering Journal, 1999, 32 (5): 10-14 |
| [10] | MINER M A. Cumulative Damage in Fatigue[J]. Journal of Applied Mechanics, 1945, 12 (3): 159-164 |
| [11] | 赵少汴, 王忠保. 抗疲劳设计-方法与数据[M]. 北京: 机械工业出版社, 1997. ZHAO Shao-bian, WANG Zhong-bao. Anti-fatigue Design:Methods and Data[M]. Beijing: China Machine Press, 1997. |
| [12] | CORTEN H T, DOLON T J. Cumulative Fatigue Damage[C]//Proceeding of the International Conference on Fatigue of Metals. London:IME, 1956:235-246. |
 2017, Vol. 34
2017, Vol. 34
