扩展功能
文章信息
- 马磊, 万水, 蒋正文
- MA Lei, WAN Shui, JIANG Zheng-wen
- 单箱多室波形钢腹板简支箱梁偏载系数简化计算方法
- A Simplified Calculation Method for Eccentric Load Coefficient of Simply Supported Single-box Multi-cell Girder with Corrugated Steel Webs
- 公路交通科技, 2017, 34(2): 62-67
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 62-67
- 10.3969/j.issn.1002-0268.2017.02.010
-
文章历史
- 收稿日期: 2016-07-11
2. 东南大学 混凝土及预应力混凝土结构教育部 重点实验室, 江苏 南京 210096;
3. 东南大学 交通学院, 江苏 南京 210096
2. Key Laboratory of Concrete and Pre-stressed Concrete Structure of Ministry of Education, Southeast University, Nanjing Jiangsu 210096, China;
3. School of Transportation, Southeast University, Nanjing Jiangsu 210096, China
为适应不断增加的车流量,采用单箱多室波形钢腹板箱梁结构的宽桥在公路和城市桥梁工程中得到推广应用,如2010年建成的单箱三室波形钢腹板箱梁桥--卫河桥[1], 2015年建成的通航孔主梁为单箱五室波形钢腹板箱梁的六塔斜拉桥--南昌朝阳大桥[2],在建的主梁为单箱四室波形钢腹板箱梁的斜拉桥--郑州朝阳沟大桥[2]等。
尽管单箱多室波形钢腹板箱梁桥建设越来越多,然而关于单箱多室波形钢腹板箱梁桥的设计规范还很匮乏。我国现有的河南省地方标准[3]要求必要时进行细致、准确的有限元分析,但有限元建模过程复杂,设计人员应用不便,实际工程设计中计算截面内力时,经常采用平面杆系单元来计算。单箱多室波形钢腹板箱梁截面宽度较大,腹板厚度较薄,作用偏心荷载时,截面的空间效应明显,需引入偏载系数[4-9]来修正平面杆系单元计算的截面应力值,从包络空间分析得到应力计算的结果。因此,单箱多室波形钢腹板箱梁的偏载系数如何取值是一个迫切需要解决的问题。
偏载系数求解时,需计算单箱多室波形钢腹板箱梁的扭转与畸变效应。国内外已有学者通过解析方法对单箱多室波形钢腹板箱梁的扭转与畸变效应[10-17]进行了研究。但分析过程中需确定约束扭转双力矩与畸变双力矩,推导过程非常复杂。本文将单箱多室波形钢腹板箱梁的腹板,近似看作等截面的梁肋,先按刚性横梁法求出活载偏心作用下边腹板的荷载横向分布系数;通过有限元建模计算单箱多室波形钢腹板箱梁的偏载系数,并对影响偏载系数的因素进行参数敏感性分析;基于偏载系数与荷载横向分布的关系,提出了偏载系数的简化计算公式。
1 荷载横向分布应用文献[13]的基本假定及计算模型,将单箱多室波形钢腹板箱梁等效为平面板梁模型,该平面板梁模型满足条件:
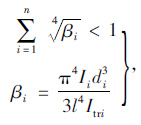
|
(1) |
式中,n为主梁数;di为主梁之间桥面板净跨度的一半;l为主梁跨度;Ii为i号主梁抗弯刚度;Itri为i号主梁单位宽度(沿桥纵向)的桥面板抗弯刚度。
应用刚性横梁法,得到各主梁的弯矩、剪力表达式。用某主梁的弯矩(剪力)除以各主梁的总弯矩(剪力),得到各主梁所分配到的弯矩(剪力)占总弯矩(剪力)的比值,即为某主梁的弯矩(剪力)横向分布影响线竖标值。
2 偏载系数 2.1 偏载系数的定义单箱多室波形钢腹板箱梁桥在偏心荷载作用下的空间应力分析比较复杂。在工程设计中,经常引入偏载系数的概念,用以修正按平面杆系计算的截面应力值,认为修正后的应力值可以包络住按空间分析得到的应力计算结果,将这种方法称之为“偏载系数法”。
偏载作用下,按空间分析得到的箱梁横截面上某点正应力为σ=σM+σW+σdW,正应力偏载系数定义为:
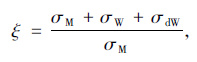
|
(2) |
式中,σM为对称荷载作用下的弯曲正应力;σW为反对称荷载作用下的约束扭转正应力;σdW为畸变翘曲正应力。
按空间分析得到的箱梁横截面上某点剪应力为τ=τM+τW+τdW,剪应力偏载系数定义为:
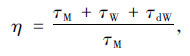
|
(3) |
式中,τM为对称荷载作用下的弯曲剪应力;τW为反对称荷载作用下的扭转剪应力;τdW为畸变翘曲剪应力。
由式(2)、(3)可知,决定偏载系数大小的因素是约束扭转应力及畸变应力之和与弯曲应力的比值。由文献[10-17]可知,单箱多室波形钢腹板箱梁的约束扭转应力及畸变应力受箱梁截面几何尺寸的影响较大。因此,下文将通过建立有限元模型并改变模型几何参数,来研究各参数对偏载系数的影响。
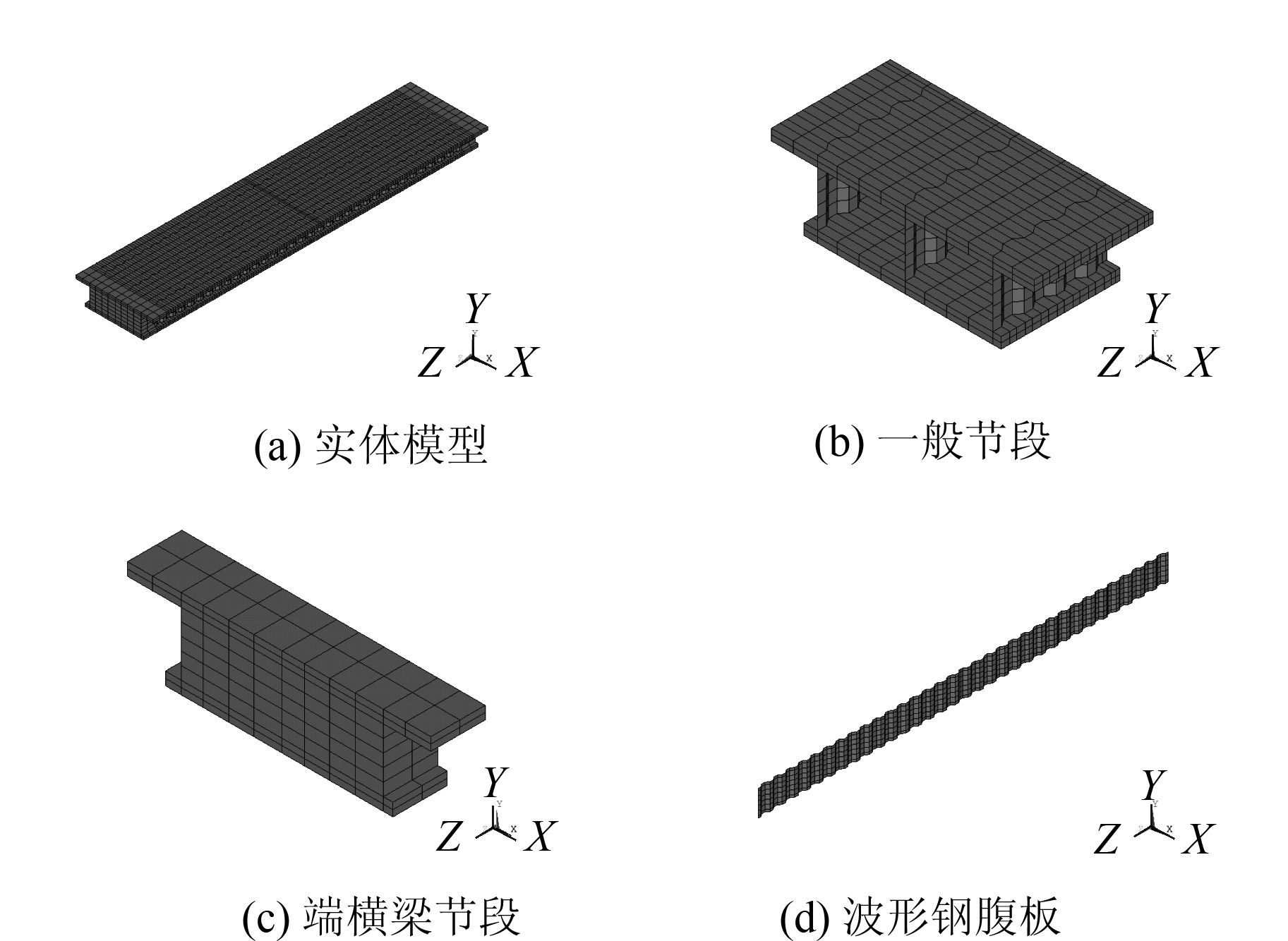
2.2 有限元计算模型以文献[13]单箱双室波形钢腹板箱梁试验梁为原型,建立ANSYS有限元模型。混凝土顶板与底板均采用SOLID45单元,波形钢腹板采用SHELL63单元。波形钢腹板与混凝土顶、底板之间视为完全固结,通过混凝土单元与波形钢腹板单元之间共节点来实现。图 1所示为网格划分后的有限元模型,共计6 232个实体单元,2 814个壳体单元。在一端底板支座垫板处约束Ux,Uy,Uz,另一端支座垫板处约束Ux,Uy。
|
| 图 1 有限元模型 Fig. 1 Finite element model |
| |
2.3 偏载系数参数敏感性分析
利用所建立的有限元模型,研究高跨比H/L、宽跨比B/L、波形钢腹板的平板长度a、波折角度γ、钢腹板厚度t、钢腹板倾角α等因素变化对单箱多室波形钢腹板组合箱梁偏载系数的影响。将H/L从0.05以0.01为增量,变化至0.09,B/L定义为单室底板宽度与跨径的比,从0.08以0.04为增量,变化至0.24。取γ为37°,a从20 mm以10 mm为增量增加至60 mm。取a不变,γ为0°,25°,37°,50°,70°。取t从1 mm以1 mm为增量变化至5 mm,α从0°以5°为增量递增至45°。分别计算各模型的正应力偏载系数及剪应力偏载系数。其中,正应力偏载系数按式(2)计算,取加载侧边腹板与底板相交角点处的值;剪应力偏载系数按式(3)计算,取加载侧边腹板高度中点处的值。因篇幅有限,仅列出偏载系数对上述各参数的敏感性,结果如图 2所示。
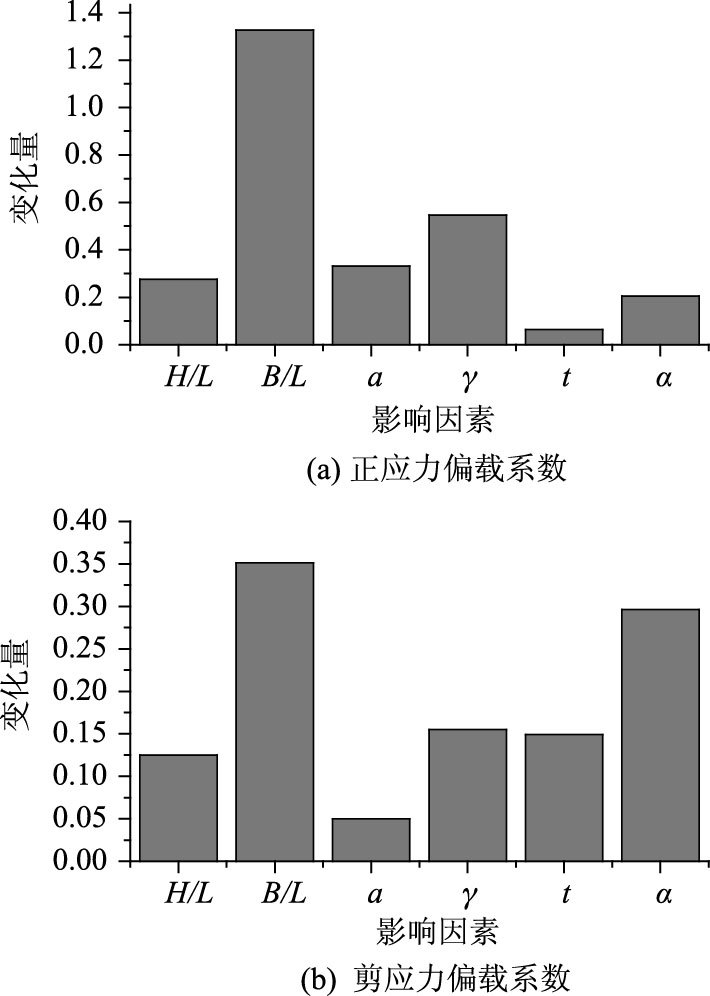
|
| 图 2 参数敏感性 Fig. 2 Parameter Sensitivity |
| |
由图 2可见,影响ξ的主要因素是B/L,其次为γ,a,之后是H/L及α,t影响最小。影响η的主要因素是B/L,其次为α,之后是γ,t,H/L,a的影响最小。
3 偏载系数简化计算公式 3.1 参数选取由图 2参数敏感性分析可知,α对ξ和η的敏感性差别较大,为分析方便,本文仅针对边腹板为直腹板的情况进行讨论,即忽略α的影响。γ, a对ξ的影响较大,但在波形钢腹板箱梁桥的设计中,最常用的波折角γ的值为31°,且我国《JT/T 784-2010组合结构桥梁用波形钢腹板》规范中,对常用a值做出了明确规定,故忽略γ、a的影响。t的影响较小,可忽略。本节针对边腹板为直腹板、室数分别为2,3,4,5的单箱多室波形钢腹板箱梁,研究B/L及H/L对偏载系数与荷载横向分布系数关系的影响。
3.2 偏载系数与荷载横向分布系数比值求解以文献[13]中的试验梁为基准模型梁,翼缘悬臂宽度保持0.2 m,令B/L以0.04为增量从0.04变化至0.24,H/L以0.01为增量从0.05变化至0.09,室数n由2变化至5,建立有限元模型。
通过所建立的120个有限元模型,计算各模型梁的偏载系数,并采用刚性横梁法计算最外侧边梁的荷载横向分布影响线竖标, 将计算所得的各模型梁的正应力偏载系数与弯矩横向分布影响线竖标值的比值、剪应力偏载系数与剪力横向分布影响线竖标的比值分别列于表 1、表 2。
由表 1、表 2可见,相对于B/L,偏载系数与荷载横向分布影响线竖标的比值随H/L的变化虽有变化,但其变化幅度很小。为简化计算,下文偏载系数简化计算公式中忽略H/L的影响。
| H/L | B/L | ||||||
| 0.04 | 0.08 | 0.12 | 0.16 | 0.20 | 0.24 | ||
| n=2 | 0.05 | 3.297 2 | 3.274 2 | 4.431 2 | 4.776 4 | 4.978 8 | 5.067 0 |
| 0.06 | 3.277 7 | 3.477 7 | 4.427 9 | 4.810 5 | 5.011 6 | 5.141 9 | |
| 0.07 | 3.250 5 | 3.614 2 | 4.423 1 | 4.831 2 | 5.064 9 | 5.191 8 | |
| 0.08 | 3.229 0 | 3.865 9 | 4.407 6 | 4.822 8 | 5.109 9 | 5.212 4 | |
| 0.09 | 3.198 8 | 4.033 9 | 4.390 5 | 4.818 4 | 5.093 8 | 5.195 9 | |
| n=3 | 0.05 | 4.713 0 | 5.772 4 | 6.345 2 | 6.540 8 | 6.369 4 | 6.150 0 |
| 0.06 | 4.704 8 | 5.769 6 | 6.402 8 | 6.612 6 | 6.607 2 | 6.351 5 | |
| 0.07 | 4.674 2 | 5.758 4 | 6.400 7 | 6.668 2 | 6.674 6 | 6.427 3 | |
| 0.08 | 4.630 5 | 5.718 0 | 6.407 8 | 6.701 3 | 6.687 4 | 6.436 6 | |
| 0.09 | 4.577 5 | 5.673 5 | 6.392 6 | 6.703 6 | 6.647 1 | 6.372 3 | |
| n=4 | 0.05 | 6.276 7 | 7.623 6 | 8.140 2 | 7.706 4 | 7.284 0 | 6.654 2 |
| 0.06 | 6.272 3 | 7.646 8 | 8.065 3 | 7.905 2 | 7.528 5 | 6.829 1 | |
| 0.07 | 6.201 6 | 7.626 8 | 8.104 8 | 8.020 9 | 7.596 9 | 6.898 8 | |
| 0.08 | 6.119 5 | 7.555 4 | 8.123 3 | 8.063 7 | 7.596 3 | 6.854 1 | |
| 0.09 | 6.026 5 | 7.518 5 | 8.111 9 | 8.007 3 | 7.531 2 | 6.751 4 | |
| n=5 | 0.05 | 7.935 2 | 9.361 9 | 9.192 4 | 8.790 2 | 7.687 8 | 6.884 7 |
| 0.06 | 7.940 1 | 9.339 0 | 9.477 3 | 9.069 5 | 7.893 3 | 7.039 5 | |
| 0.07 | 7.809 7 | 9.337 2 | 9.538 3 | 9.145 2 | 7.948 4 | 7.076 7 | |
| 0.08 | 7.704 4 | 9.341 1 | 9.544 1 | 9.151 7 | 7.936 6 | 7.054 4 | |
| 0.09 | 7.562 9 | 9.249 0 | 9.491 1 | 9.079 7 | 7.829 9 | 6.952 6 | |
| H/L | B/L | ||||||
| 0.04 | 0.08 | 0.12 | 0.16 | 0.20 | 0.24 | ||
| n=2 | 0.05 | 2.198 2 | 2.264 4 | 2.199 5 | 2.205 3 | 2.213 2 | 2.198 6 |
| 0.06 | 2.180 1 | 2.210 7 | 2.196 0 | 2.251 2 | 2.281 2 | 2.282 3 | |
| 0.07 | 2.164 1 | 2.193 3 | 2.243 9 | 2.346 5 | 2.399 8 | 2.399 4 | |
| 0.08 | 2.145 8 | 2.130 6 | 2.311 3 | 2.446 6 | 2.520 3 | 2.503 8 | |
| 0.09 | 2.129 4 | 2.103 5 | 2.394 3 | 2.552 8 | 2.621 7 | 2.594 7 | |
| n=3 | 0.05 | 2.700 1 | 2.716 7 | 2.765 1 | 2.814 1 | 2.775 6 | 2.688 9 |
| 0.06 | 2.666 4 | 2.705 9 | 2.848 7 | 2.947 5 | 2.960 9 | 2.851 6 | |
| 0.07 | 2.640 2 | 2.761 0 | 3.047 0 | 3.144 9 | 3.151 8 | 3.018 6 | |
| 0.08 | 2.619 4 | 2.845 0 | 3.172 9 | 3.339 7 | 3.319 9 | 3.117 0 | |
| 0.09 | 2.610 5 | 2.957 5 | 3.360 6 | 3.522 5 | 3.464 8 | 3.262 7 | |
| n=4 | 0.05 | 3.088 6 | 3.198 2 | 2.751 3 | 3.307 8 | 3.221 3 | 3.803 4 |
| 0.06 | 3.047 3 | 3.222 0 | 3.459 2 | 3.541 1 | 3.458 1 | 4.036 9 | |
| 0.07 | 3.029 2 | 3.368 2 | 3.720 0 | 3.831 5 | 3.700 7 | 4.288 2 | |
| 0.08 | 3.029 2 | 3.549 5 | 3.995 0 | 4.099 6 | 3.907 2 | 4.489 9 | |
| 0.09 | 3.057 2 | 3.770 1 | 4.267 2 | 4.327 3 | 4.081 6 | 4.668 9 | |
| n=5 | 0.05 | 3.461 9 | 3.601 2 | 3.773 6 | 3.737 4 | 4.295 7 | 4.673 9 |
| 0.06 | 3.413 5 | 3.713 4 | 4.055 4 | 4.045 1 | 4.589 5 | 4.973 5 | |
| 0.07 | 3.406 1 | 3.959 0 | 4.410 0 | 4.388 1 | 4.935 3 | 5.280 1 | |
| 0.08 | 3.441 1 | 4.257 4 | 4.766 2 | 4.700 9 | 5.240 5 | 5.553 8 | |
| 0.09 | 3.512 2 | 4.572 3 | 5.105 2 | 4.974 8 | 5.494 2 | 5.777 0 | |
3.3 偏载系数简化计算公式
当n=2, 3, 4, 5, 0.04≤B/L≤0.24时,单箱多室波形钢腹板箱梁偏载系数与边腹板处工字梁的荷载横向分布影响线竖标的关系式:
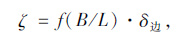
|
(5) |
式中,ζ为正应力(剪应力)偏载系数;f(B/L)为正应力(剪应力)偏载系数与边腹板处工字梁的弯矩(剪力)横向分布影响线竖标的拟合函数关系式;δ边为边腹板处工字梁的荷载横向分布影响线竖标。
基于最小二乘法,得到了偏载系数与荷载横向分布影响线竖标的比值关于B/L的三次函数关系式:
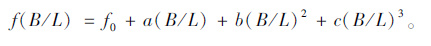
|
(6) |
正应力及剪应力函数关系式各参数f0, a, b, c的取值分别如表 3、表 4所示。
| 室数n | f0 | a | b | c | R |
| 2 | 2.808 | 7.875 | 70.772 | -262.949 | 0.992 |
| 3 | 3.035 | 47.854 | -190.713 | 203.284 | 0.999 |
| 4 | 3.666 | 79.037 | -426.574 | 632.552 | 0.999 |
| 5 | 4.569 | 105.689 | -673.665 | 1 146.687 | 0.995 |
| 室数n | f0 | a | b | c | R |
| 2 | 2.236 | -3.465 | 44.679 | -114.598 | 0.998 |
| 3 | 2.517 | 1.710 | 39.768 | -161.82 | 0.990 |
| 4 | 2.055 | 32.187 | -219.443 | 511.950 | 0.946 |
| 5 | 2.438 | 32.241 | -189.224 | 434.476 | 0.976 |
4 简化公式的验证
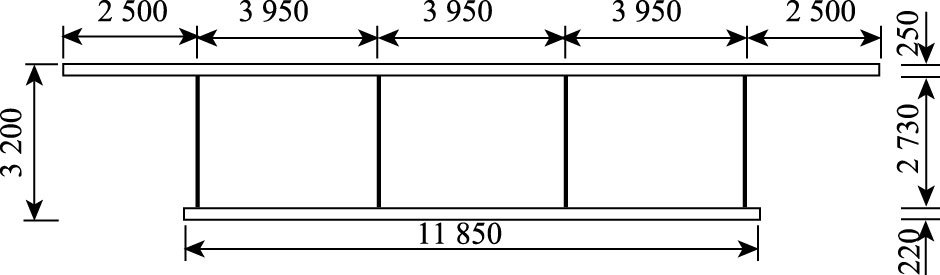
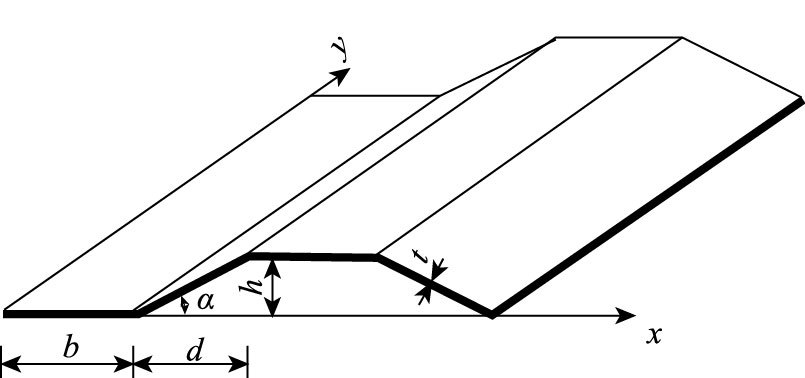
某跨径为52 m的单箱三室波形钢腹板简支箱梁桥,不考虑上下翼缘板的加腋,横截面可简化为图 3所示的箱形截面。波形钢腹板的波纹形状如图 4所示,厚度t=0.012 m,波长直板段b=0.33 m,波长斜板段的水平长度d=0.27 m,波折角α=36.53°,波高h=0.2 m。
|
| 图 3 横截面(单位:mm) Fig. 3 Cross-section (unit:mm) |
| |
|
| 图 4 波纹形状 Fig. 4 Corrugation configuration |
| |
将图 3所示的箱梁截面换算为混凝土截面,并划分为4个工字型截面梁。划分后的箱梁等效转化为有4根纵向主梁的平面板梁模型,计算截面各参数值结果如表 5所示。
| 梁号 | Ii/m4 | Itri/m4 | di/m | l/m | βi |
| 1 | 117.455 3 | 184.984 1 | 1.975 | 52 | 0.000 02 |
| 2 | 117.455 3 | 253.413 3 | 1.975 | 52 | 0.000 014 |
| 3 | 117.455 3 | 253.413 3 | 1.975 | 52 | 0.000 014 |
| 4 | 117.455 3 | 184.984 1 | 1.975 | 52 | 0.000 02 |
将各参数代入式(1),得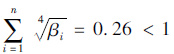
| 类型 | f0 | a | b | c | f (B/L) | δ边 | ζ |
| 正应力 | 3.035 | 47.854 | -190.713 | 203.284 | 5.637 05 | 0.296 3 | 1.67 |
| 剪应力 | 2.517 | 1.710 | 39.768 | -161.82 | 2.805 6 | 0.695 | 1.95 |
通过文献[10-12]的解析方法求解截面的各应力值,进而求得正应力偏载系数及剪应力偏载系数,记为理论解,并如第2节所述方法建立有限元模型,计算偏载系数的有限元解,本文提出的简化计算方法计算结果与上述两种方法计算的结果进行对比,如表 7所示。
| 类型 | 理论 (1) | 有限元 (2) | 简化 式(3) | 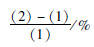 | 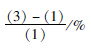 |
| 正应力 | 1.45 | 1.44 | 1.67 | 0.05 | 15.22 |
| 剪应力 | 1.92 | 2.14 | 1.95 | 11.81 | 1.6 |
由表 7可见,本文提出的简化公式计算的正应力偏载系数与有限元的误差在15%左右,剪应力偏载系数与有限元的误差在2%左右,基本满足工程应用的精度要求。
5 结论(1) 影响正应力偏载系数及剪应力偏载系数的最主要因素是宽跨比。
(2) 本文提出的偏载系数简化公式适用求解不超过5室,单室宽度与跨径的比值介于0.08~0.24的单箱多室波形钢直腹板箱梁的正应力偏载系数及剪应力偏载系数。
| [1] | 万水, 李淑琴, 马磊. 波形钢腹板预应力混凝土组合箱梁结构在中国桥梁工程中的应用[J]. 建筑科学与工程学报, 2009, 26 (2) : 15-20 WAN Shui, LI Shu-qin, MA Lei. Application of Prestressed Concrete Composite Box-girder Structure with Corrugated Steel Webs in Bridge Engineering in China[J]. Journal of Architecture and Civil Engineering, 2009, 26 (2): 15-20 |
| [2] | 邓国良, 陈静, 邓文琴, 等. 波形钢腹板组合结构矮塔斜拉桥的发展与应用[J]. 中外公路, 2016, 36 (3) : 98-102 DENG Guo-liang, CHEN Jing, DENG Wen-qin, et al. Application and Development of Extradosed Cable-stayed Bridges with Corrugated Steel Webs[J]. China and Foreign Highway, 2016, 36 (3): 98-102 |
| [3] | DB41-T 643-2010, 公路波形钢腹板预应力混凝土箱梁桥设计规范[S]. DB41-T 643-2010, Code for Design of the Prestressed Concrete Box-girder Highway Bridge with Corrugated Steel Webs[S]. |
| [4] | 刘保东, 任红伟, 李鹏飞, 等. 波纹钢腹板组合箱梁偏心增大系数计算方法[J]. 公路交通科技, 2012, 29 (3) : 80-85 LIU Bao-dong, REN Hong-wei, LI Peng-fei, et al. Calculation Methods of Eccentric Magnified Factor of Concrete Box Girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2012, 29 (3): 80-85 |
| [5] | 刘琪, 吴忠华, 付坤. 独塔单索面混合梁斜拉桥偏载扭转效应分析[J]. 桥梁建设, 2011 (6) : 42-45 LIU Qi, WU Zhong-hua, FU Kun. Analysis of Eccentric Load Torsional Effect of Hybrid Girder Cable-Stayed Bridge with Single Pylon and Single Cable Plane[J]. Bridge Construction, 2011 (6): 42-45 |
| [6] | 项贻强, 何余良, 刘丽思, 等. 考虑滑移的多梁式组合小箱梁桥荷载横向分布[J]. 哈尔滨工业大学学报, 2012, 44 (8) : 113-118 XIANG Yi-qiang, HE Yu-liang, LIU Li-si, et al. Lateral Load Distribution of Multi-box Steel-concrete Composite Girder Bridges for Considering Slipping Effect[J]. Journal of Harbin Institute of Technology, 2012, 44 (8): 113-118 |
| [7] | 陈国强. 连续宽箱梁的偏载增大系数的讨论[J]. 公路交通科技, 2013, 30 (7) : 66-71 CHEN Guo-qiang. Discussion on Eccentric Load Enhancement Coefficient of Continuous Wide Box Girder[J]. Journal of Highway and Transportation Research and Development, 2013, 30 (7): 66-71 |
| [8] | 王雷.现浇中小跨径连续单箱多室宽箱梁桥空间效应研究[D].北京:北京交通大学, 2013. WANG Lei. Spatial Effect of Cast-in-place Small and Medium Span Continuous Wide-box Girder with Multi-cells[D].Beijing:Beijing Jiaotong University, 2013. |
| [9] | 任红伟.波纹钢腹板预应力混凝土组合箱梁设计理论与试验研究[D].北京:北京交通大学, 2011. REN Hong-wei. Research on Design Theory and Experiment of Prestressed Concrete Composite Box Girder with Corrugated Steel Webs[D]. Beijing:Beijing Jiaotong University, 2011. |
| [10] | 杨丙文, 黎雅乐, 万水, 等. 波形钢腹板箱梁畸变应力分析[J]. 东南大学学报:自然科学版, 2011, 41 (5) : 1065-1069 YANG Bing-wen, LI Ya-le, WAN Shui, et al. Stress Analysis of Box Girders with Corrugate Steel Webs under Distorsion[J]. Journal of Southeast University:Natural Science Edition, 2011, 41 (5): 1065-1069 |
| [11] | 姚森.变截面波形钢腹板组合箱梁扭转与畸变分析[D].南京:东南大学, 2010. YAO Sen. Analysis on Restrained Torsion and Distortion of Variable Depth Composite PC-box-girder with Corrugated Steel Webs[D]. Nanjing:South East University, 2010. |
| [12] | 易永峰.单箱三室波形钢腹板箱梁扭转分析[D].南京:东南大学, 2010. YI Yong-feng. Analysis on Torsion of Single-box Three Cell Box Girder with Corrugated Steel Webs[D]. Nanjing:South East University, 2010. |
| [13] | 马磊, 万水, 蒋正文, 等. 单箱多室波形钢腹板箱梁荷载横向分布[J]. 东南大学学报, 2014, 44 (1) : 145-149 MA Lei, WAN Shui, JIANG Zheng-wen, et al. Load Transverse Distribution of Single Box Multi-cell Girder with Corrugated Steel Webs[J]. Journal of Southeast University:Natural Science Edition, 2014, 44 (1): 145-149 |
| [14] | DING Yong, JIANG Ke-bin, LIU Ya-wen. Nonlinear Analysis for PC Box-girder with Corrugated Steel Webs under Pure Torsion[J]. Thin-Walled Structures, 2012, 51 : 167-173 |
| [15] | JIANG Ke-bin, DING Yong, YANG Jian-kui. Experimental Study on Ultimate Torsional Strength of PC Composite Box-girder with Corrugated Steel Webs under Pure Torsion[J]. Structural Engineering and Mechanics, 2013, 46 (4): 519-531 |
| [16] | HE Jun, LIU Yu-qing, CHEN Ai-rong, et al. Mechanical Behavior and Analysis of Composite Bridges with Corru-gated Steel Webs:State-of-the-art[J]. International Journal of Steel Structures, 2012, 12 (3): 321-338 |
| [17] | EL METWALLY A, LOOV R E. Corrugated Steel Webs for Prestressed Concrete Girders[J]. Materials and Structures, 2003, 36 (2): 127-134 |
 2017, Vol. 34
2017, Vol. 34
