扩展功能
文章信息
- 张俊荣, 陈保国, 易贤龙, 谭钦文, 王坤鹏
- ZHANG Jun-rong, CHEN Bao-guo, YI Xian-long, TAN Qin-wen, WANG Kun-peng
- 两侧水位变化时路堤渗流特征及稳定性分析
- Analysis on Seepage Characteristics and Stability of Embankment with Water Level Change on both Sides
- 公路交通科技, 2017, 34(2): 35-41
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 35-41
- 10.3969/j.issn.1002-0268.2017.02.006
-
文章历史
- 收稿日期: 2016-01-05
影响浸水路堤稳定性的因素多种多样,国内外专家在浸水路堤影响因素分析方面均进行了相关研究并取得了一定的成果。Richards[1]将达西定律推广应用到岩土体介质的非饱和渗流问题的研究中,推动了浸水边坡的非稳定渗流理论研究。N. I. Roslan[2]等通过CBR试验研究了不同浸水情况下路面填土材料的承载力变化。Kanchana H.J[3]等通过不同配合比土样试验验证了土的配合比对土质水坝的抗渗性以及土质坝的稳定性影响。范亮[4]以室内模型试验的方式,研究并探讨了水位高低、路堤高度、加筋、填料性质等因素对浸水高填方路堤侧向变形和竖向变形的影响。李勇[5]、贾建彬[6]采用有限元的方式分别分析了水位升降变化、交通荷载、水位升降变化、土工格栅刚度和布设方式对浸水路堤变形和稳定的影响。楼晓昱[7]利用数值模拟结合饱和不饱和渗流理论研究了水位升降对沿湖路堤边坡稳定性的影响以及渗流特征。梁燕等[8]研究了路堤高度坡率、次级边坡高度和水位降幅对水位骤降后高土石路堤稳定性的影响,得出各影响因素的重要性大小顺序。
本文在前人的基础上[9],研究多因素影响下两侧有水的浸水路堤内的渗流特征、路堤稳定性、堤内土体变形变化规律,以单侧水位变化下黏性素填土浸水路堤为研究对象,基于正交试验设计方法设计数值模拟计算方案,分析比较路堤高度、水位降幅、水位降速、渗透系数等因素对路堤稳定性影响的重要程度。
1 数值分析模型为研究浸水路堤在水位变动下的渗流场、应力场和变形特征,采用Geo-Studio软件进行相关数值模拟计算。首先通过SEEP/W计算模块获取浸水路堤的渗流场信息,再将其代入SLOPE/W模块中进行浸水渗透过程中边坡稳定性分析,最后再导入SIGMA/W模块,计算堤内位移的变化情况。
在路堤模型分析中所用填土材料和底部河床黏性土物理力学计算参数如表 1所示。模型分析采用扩展的Mohr-Coulomb本构模型,边坡稳定性计算方法采用Morgenstern-Price法,滑动面位置设为自动。假设浸水路堤模型内部初始水位线与外部水位线等高,路堤具体高度视研究条件而定,基质吸力曲线采用软件自带相应土体函数。
| 土类 | 湿重度/ (kN·m-3) | 有效内摩擦角/ (°) | 有效黏聚力/ kPa | 有效弹性模量/ MPa | 有效泊松比 | 饱和渗透系数/ (m·s-1) |
| 砂性土 | 18 | 27.6 | 4 | 20 | 0.25 | 2×10-4 |
| 黏性土 | 19 | 21 | 18 | 10 | 0.25 | 6×10-7 |
| 河床土 | 18.5 | 25 | 12 | 10 | 0.25 | 6×10-7 |
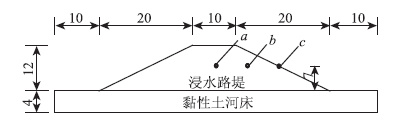
为简化计算条件,并参照规范[10]中对浸水路堤设计的相关规定,建立如图 1所示浸水路堤计算模型,路堤边坡为简单梯形断面,坡体为砂性土或黏性土均质土样,下部河床为黏土,图中a,b,c这3点为路堤内3个渗流计算点,高度为7 m。
|
| 图 1 浸水路堤外形(单位:m) Fig. 1 Shape of immerseable embankment (unit:m) |
| |
当计算浸水路堤位移时,假设河床断面左侧、右侧和底部为不透水边界。河床断面底部边界X和Y方向的位移均设为0,左侧与右侧边界X方向位移设为0,Y方向自由。路堤内土体采用弹塑性材料,河床黏土采用线弹性材料。
研究浸水路堤在水位变化下的相关规律时,针对不同研究因素,对路堤模型假设条件可作相应调整, 并基于以下几点假设开展:(1)不考虑路堤交通荷载,假设路堤高度为13 m;(2)路堤两侧水位初始高度相同,水位降低过程中匀速变化;(3)考虑单侧水位变化时,路堤左侧水位设为恒定。水位不同降速值如表 2所示。
由于水位变化因素研究中已分析单双侧水位变化的影响,针对路堤高度影响因素研究时仅选择最不利的状况也即单侧水位变化下的不同高度路堤进行分析。假设堤内土体及边界假定条件不变,不考虑路堤交通荷载作用,不同路堤高度设定值如表 3所示。
当研究单一影响因素为渗透系数时,采用单侧水位变化下的不同渗透系数填土路堤。堤内土体及边界假定条件不变,将粉砂土和粉质黏土渗透系数按规范[12]所给定范围划分为5个参数值,划定结果如表 4所示。
| 土类 | K1 | K2 | K3 | K4 | K5 |
| 砂性土/ (m·s-1) | 1.15× 10-5 | 2.36× 10-5 | 3.58× 10-5 | 4.79× 10-5 | 6× 10-5 |
| 黏性土/ (m·s-1) | 1.15× 10-6 | 1.585× 10-6 | 2.02× 10-6 | 2.45× 10-6 | 2.89× 10-6 |
2 计算结果及分析 2.1 不同影响因素下堤内渗流特征分析
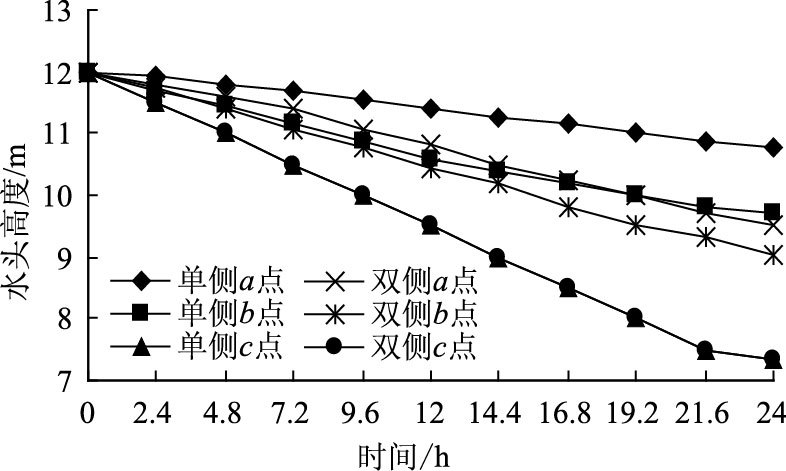
绘制砂性土浸水路堤单侧、双侧水位变化下堤内图 1中a,b,c共3处总水头与时间关系曲线,如图 2所示。
|
| 图 2 三点水头变化图 Fig. 2 Changes of water head at three positions |
| |
由双侧水位变化时a,b,c三点处水头变化图可知,三点处水头随路堤外侧水位降低而同时开始降低,水头降低速度由外而内逐渐减小,具有一定的滞后性,这一浸润线变化的滞后性对边坡产生了持续渗透动水压力作用。三点处水头降速的变化规律反映了堤内水头变化速度受到渗流路径的影响。
而单侧水位变化时,图中a,b,c的水头下降速度比双侧水位降低时同点处慢。堤内a,c两点水头变化差异比双侧水位降低时增加,堤内水位变化的滞后性更加明显。分析认为,双侧水位降低时,堤内外水头差随渗流活动逐渐减小。单侧水位降低时浸水路堤左侧与右侧水位间的水头差等于降幅的大小,由于左侧水位恒定,这一水头差保持不变。在渗流持续一段时间后,单侧水位降低形成的水头差逐渐大于双侧水位降低形成的水头差,造成水流的滞后性增加。
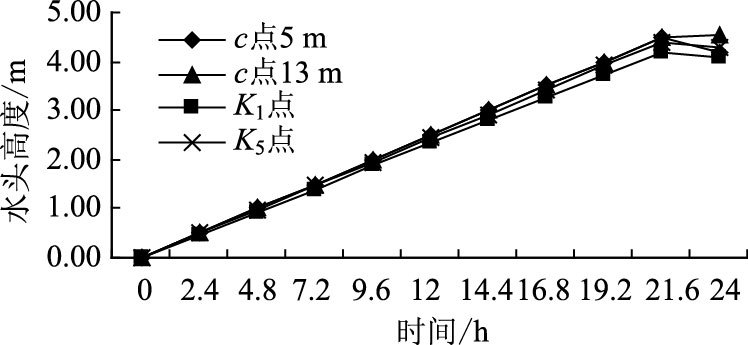
绘制K1和K5渗透系数下以及5 m和13 m高路堤内水位最终位置高度处的c点处水位降低过程中的总水头变化量与时间关系曲线如图 3所示。
|
| 图 3 水头变化量-时间关系图 Fig. 3 Water head variation vs. time |
| |
在路堤高度增加时,路堤内c点处水头总变化量相应增加。分析认为当路堤高度减小时,路堤体积相应减小,堤内含水量随之而减小,因而c点处水头变化较快。同时由于路堤高度的增加带来宽度上的相应增加,渗流路径相应变化导致堤内水排出时间增加。
K1渗透系数下,路堤内c点处水头高度变化量为4.2 m;K5渗透系数下,路堤内c点处水头高度变化量为4.4 m。随着渗透系数增大,在堤内同一位置处的水头变化增大。当水位下降时,渗流量随渗透系数的增加而增加。渗透系数的增加减小了渗流时间,降低了渗流的滞后性带来的渗透动水压力,从而削弱渗流的破坏作用。
2.2 不同影响因素下路堤稳定性分析浸水路堤失稳的根本原因有两个。一方面,水位以下路堤填料含水量在水流的长期浸泡作用下会逐渐上升,导致其物理力学性质大大降低,受软化作用影响会失去其原有设计抗剪强度;另一方面,当路堤一侧或两侧水位下降时,路堤内产生向外的渗透压力会增加其所受的剪应力,同时向外的路堤渗流还会带走微小颗粒物,在路堤内形成潜在滑动面,对路堤边坡的滑动提供初始条件。
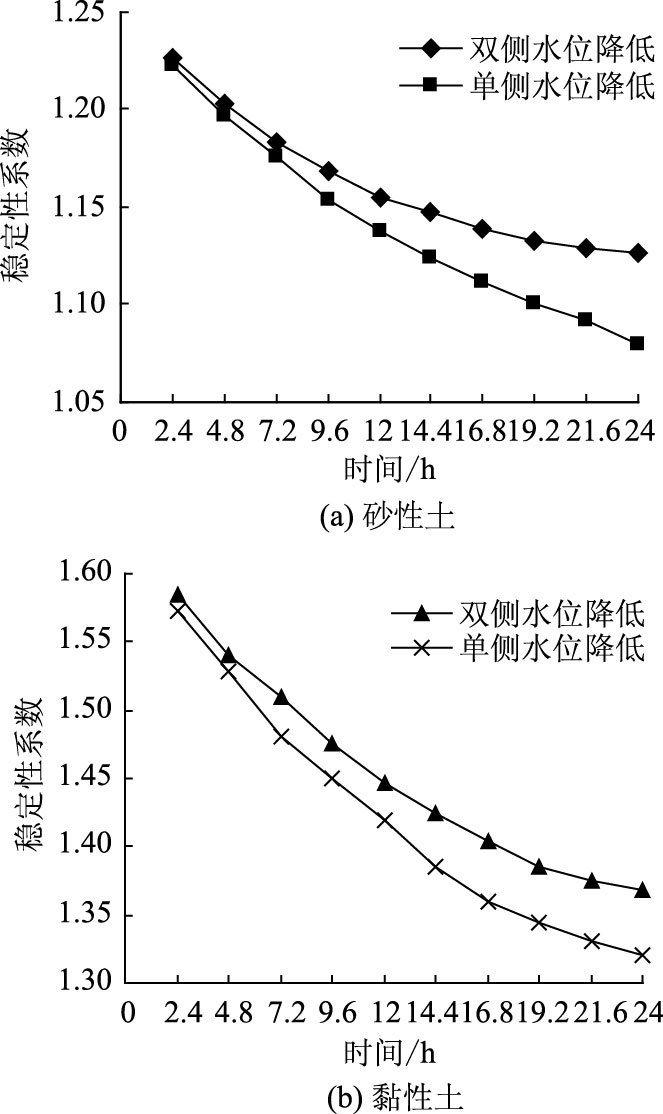
不同填土路堤边坡稳定性系数与水位降幅的关系如图 4所示。
|
| 图 4 稳定性系数与时间关系 Fig. 4 FOS vs. time |
| |
由于路堤两侧水位降速一定,图 4中边坡最终稳定性系数与时间的关系即与水位降幅的关系。对于砂性土路堤,路堤边坡稳定性系数随着两侧水位降幅的增加而逐渐降低,降低速度随着降幅增加逐渐放缓。单侧水位变化时,路堤边坡稳定性系数随着水位降幅的增加而快速降低。当两侧水位差扩大时,渗流对边坡稳定性的影响加大,表现为路堤稳定性系数的降低速度先减缓后增加。在同降速不同降幅下,单侧稳定性系数变化明显大于双侧,单侧水位降低时降幅的变化对边坡稳定性的影响明显更大。
黏性土路堤边坡稳定性随着单侧水位降幅的增加的变化规律与砂性土一致,但是黏性土路堤稳定性系数变化幅度较大,水位降幅的变化对黏性土路堤稳定性的影响大于砂性土。由于黏性土砂性土浸水路堤稳定性系数差异较大,下面选砂性土路堤为研究对象。
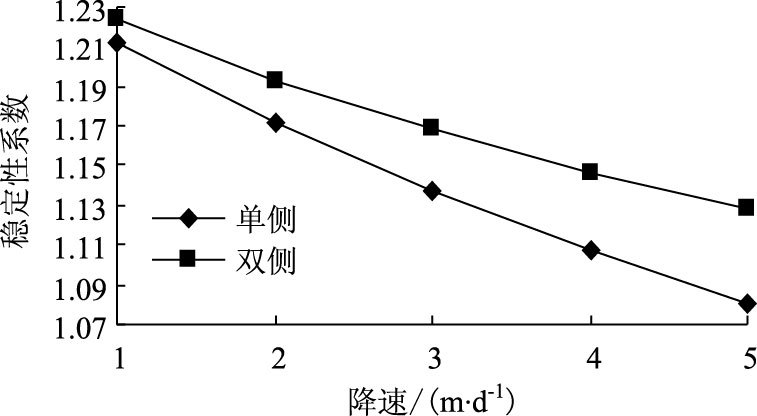
砂性土路堤单侧、双侧水位变化下边坡稳定性系数与降速值关系如图 5所示。
|
| 图 5 稳定性系数与降速关系 Fig. 5 FOS vs. water level educing speed |
| |
双侧水位下降,边坡稳定性系数随着降速的增加而降低,当降速为1 m/d时,路堤稳定性系数为1.224;当降速为5 m/d时,路堤稳定性系数为1.128。稳定性系数与降速的增加非线性负相关,水位降速越大,稳定性系数降低越慢。
当路堤单侧水位降低时,边坡稳定性系数随着降速的增加而降低,当降速为1 m/d时,路堤边坡稳定性系数为1.212;当降速为5 m/d时,路堤稳定性系数为1.081。稳定性系数与降速的增加非线性负相关,水位降速越大,稳定性系数降低越慢。
在同降幅不同降速下,单侧水位降低引起的稳定性系数降低了0.131,两侧水位降低时这一幅度为0.096。水位变化的速度在单侧水位降低时对边坡稳定性的影响更大。
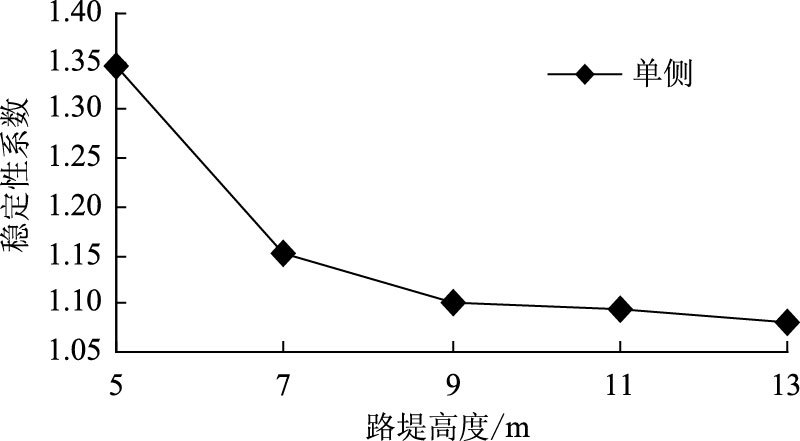
单侧水位变化时,砂性土路堤边坡稳定性系数在不同路堤高度下的最终值与路堤高度关系如图 6所示。
|
| 图 6 稳定性系数与高度关系 Fig. 6 FOS vs. height |
| |
当路堤右侧水位降低时,边坡稳定性系数与路堤高度的增加非线性相关。当高度为5 m时,路堤边坡稳定性系数为1.345;当高度为13 m时,路堤边坡稳定性系数递减为1.085,边坡稳定性接近极限平衡状态。边坡稳定性系数随着路堤高度的增加而降低,降低速率随着高度的增加放缓。
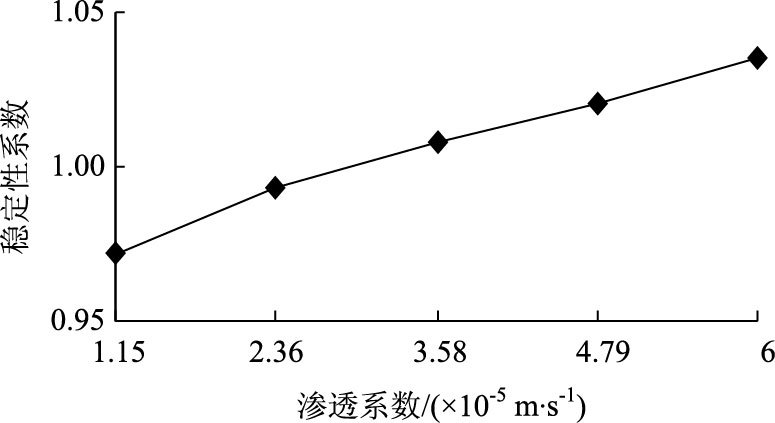
砂性土路堤边坡稳定性系数与渗透系数的关系如图 7所示。
|
| 图 7 稳定性系数与渗透系数关系 Fig. 7 FOS vs. permeability coefficient |
| |
在路堤其他假设条件不变的情况下,当渗透系数为K1时,路堤边坡稳定性系数为0.972,边坡处于不稳定状态;当渗透系数为K5时,路堤稳定性系数相比K1增加到1.035;路堤边坡稳定性系数与渗透系数非线性正相关。
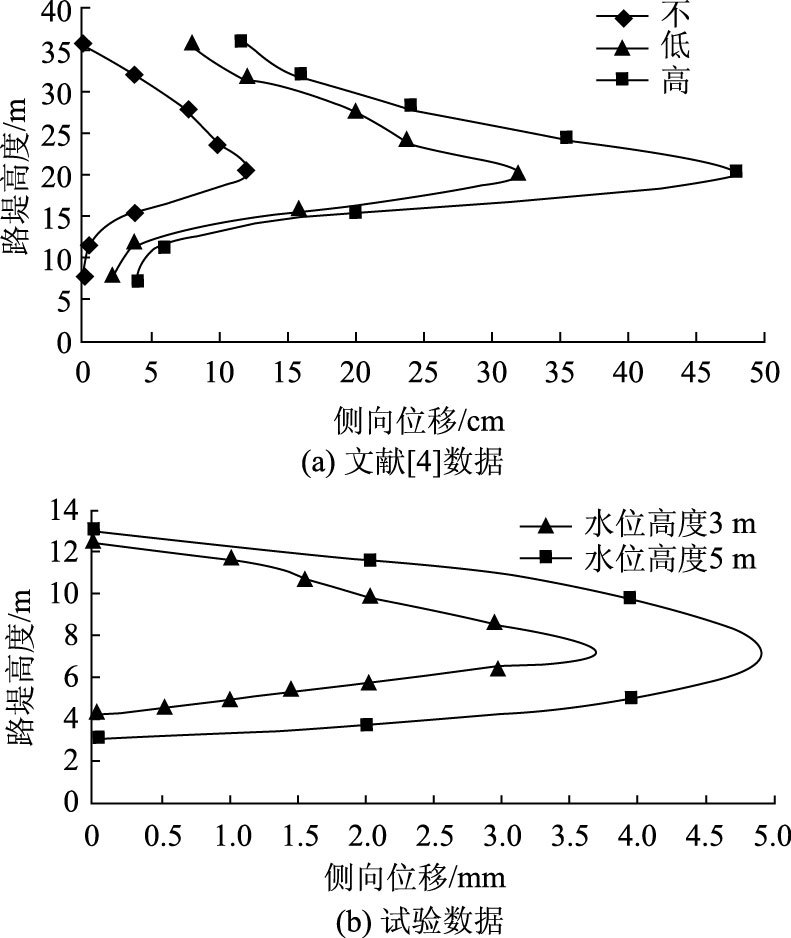
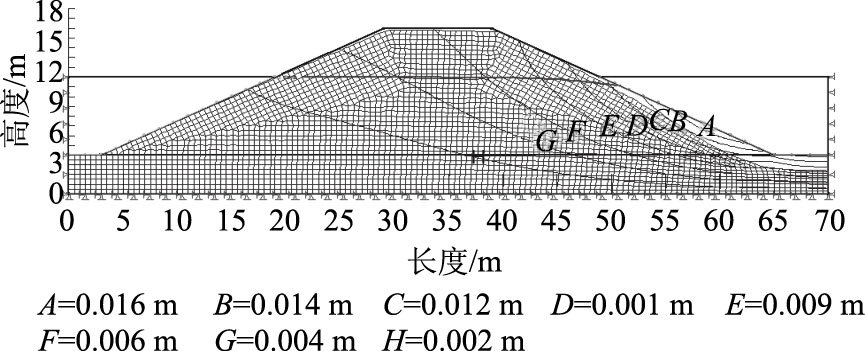
2.3 堤内位移分析通过数值模拟求解水位变化影响下路堤堤内位移值,选取黏性土路堤水位高度与路堤高度影响下侧向位移分布规律结果,并与文献[4]中的试验数据进行比较,比较结果如图 8所示。图中可以看出,当路堤水位发生变化时,路堤侧向位移主要集中在路堤中部,且随着水位高度的增加而增加,数值模拟结果所得到的变形规律与实际试验吻合。图 9为5 m降幅下单侧水位变化后路堤内最大位移分布情况,图中可见单侧水位降低时,路堤最大位移发生在右侧(也即背水面)坡面中下部。计算发现,路堤最大位移随着水位变化向坡面下部发展。随着降幅从1 m增加到5 m,坡面靠坡脚处最大位移由3.2 mm发展到18 mm,边坡变形幅度增大。当单侧水位降低时,应当注意此处加固。
|
| 图 8 侧向位移与水位关系 Fig. 8 Lateral displacement vs. water level |
| |
|
| 图 9 路堤内最大位移分布 Fig. 9 Distribution of max displacement inside embankment |
| |
3 影响因素重要性分析 3.1 正交试验设计
选择单侧水位变化下黏性土路堤为研究对象,研究4个影响因素,即水位降幅(A)、水位降速(B)、路堤高度(C)、渗透系数(D)对路堤稳定性的影响,其中4个因素取5个水平,采用全面试验法总共有54=625个不同水平组合,对不同影响因素做625次试验比较,工作量是非常巨大的。
正交试验设计法从全面试验中挑选部分有代表性的点进行试验,得到最优或最劣因素组合,并以贡献率评价各因素影响大小,大大减小工作量,是一种高效、快速、经济的试验方法。因此,本文采用正交试验设计方法设计数值计算内容,以稳定性系数为考察指标评定各水平组合好坏,4个因素的相关参数设定如前文所述。
选择正交试验设计表如表 5所示,其中Tq为某因素在q水平时相应计算结果平均值。
| 试验号 | A | B | C | D | 稳定性 系数 |
| 水位 降幅/m | 水位降速/ (m·d-1) | 路堤 高度/m | 渗透系数/ (m·s-1) | ||
| 1 | 1 | 1 | 5 | 1.15×10-6 | 2.725 |
| 2 | 1 | 2 | 7 | 1.585×10-6 | 2.187 |
| 3 | 1 | 3 | 9 | 2.02×10-6 | 1.975 |
| 4 | 1 | 4 | 11 | 2.45×10-6 | 1.633 |
| 5 | 1 | 5 | 13 | 2.89×10-6 | 1.184 |
| 6 | 2 | 1 | 7 | 2.02×10-6 | 1.902 |
| 7 | 2 | 2 | 9 | 2.45×10-6 | 1.794 |
| 8 | 2 | 3 | 11 | 2.89×10-6 | 1.550 |
| 9 | 2 | 4 | 13 | 1.15×10-6 | 1.117 |
| 10 | 2 | 5 | 5 | 1.585×10-6 | 2.256 |
| 11 | 3 | 1 | 9 | 2.89×10-6 | 1.669 |
| 12 | 3 | 2 | 11 | 1.15×10-6 | 1.361 |
| 13 | 3 | 3 | 13 | 1.585×10-6 | 1.078 |
| 14 | 3 | 4 | 5 | 2.02×10-6 | 1.982 |
| 15 | 3 | 5 | 7 | 2.45×10-6 | 1.697 |
| 16 | 4 | 1 | 11 | 1.585×10-6 | 1.399 |
| 17 | 4 | 2 | 13 | 2.02×10-6 | 1.065 |
| 18 | 4 | 3 | 5 | 2.45×10-6 | 1.810 |
| 19 | 4 | 4 | 7 | 2.89×10-6 | 1.579 |
| 20 | 4 | 5 | 9 | 1.15×10-6 | 1.481 |
| 21 | 5 | 1 | 13 | 2.45×10-6 | 1.076 |
| 22 | 5 | 2 | 5 | 2.89×10-6 | 1.817 |
| 23 | 5 | 3 | 7 | 1.15×10-6 | 1.513 |
| 24 | 5 | 4 | 9 | 1.585×10-6 | 1.353 |
| 25 | 5 | 5 | 11 | 2.02×10-6 | 1.295 |
| T1 | 1.941 | 1.754 | 2.118 | 1.639 | |
| T2 | 1.724 | 1.645 | 1.776 | 1.655 | |
| T3 | 1.557 | 1.585 | 1.654 | 1.644 | |
| T4 | 1.467 | 1.533 | 1.448 | 1.575 | |
| T5 | 1.411 | 1.582 | 1.104 | 1.560 |
3.2 影响因素主成分分析
各影响因素对路堤稳定性的影响大小可以通过贡献率来表示。贡献率可以通过式(1)~(4)计算[8]。
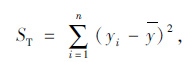
|
(1) |
式中,ST表示试验结果波动的总平方和;n是试验次数;yi为各次试验结果,i=1, 2, 3…;y为试验得结果的总平均值,计算公式如式(2)所示。
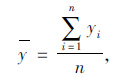
|
(2) |
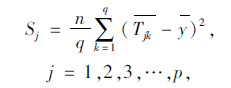
|
(3) |
式中,Sj为第j列(即第j个因子)的平方和,它表示由于j因子的不同水平所引起的试验结果的波动。Sj中除了因子的效应外,还包含误差。本文在各次数值计算中,除4个影响因子的变化外,其他条件均严格保持不变,如路堤填土材料的物理力学性质指标、网格划分、单侧水位变化等,因而不同次的数值计算所引起的误差可以不考虑。
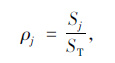
|
(4) |
式(4)为第j因子的贡献率计算公式,式中,ρj为第j因子的贡献率;Sj为j因子的平方和。计算结果如表 6所示。
| 因素 | 平方和 | 贡献率/% |
| A | 0.924 6 | 22.73 |
| B | 0.144 1 | 3.54 |
| C | 2.846 7 | 69.97 |
| D | 0.038 9 | 0.96 |
| 总平方和 | 4.068 3 | - |
由分析可知,正交试验中的4个影响因素的贡献率分别为22.73%, 3.54%, 69.97%, 0.96%,其重要程度由大到小排序依次为路堤高度>水位降幅>水位降速>渗透系数。在影响单侧水位变化下黏性素填土浸水路堤稳定性的因素中,路堤高度的选择是最重要的,渗透系数是最不重要的。
4 结论(1) 浸水路堤堤内水头降低速度由外而内逐渐降低,具有一定的滞后性,这一浸润线变化的滞后性对边坡产生了持续渗透动水压力作用。渗流的滞后性受渗流路径、水头差、渗透系数的影响。
(2) 路堤边坡稳定性系数随着堤外水位降幅、降速、路堤高度的增加而逐步降低,降低速率逐渐放缓;随着渗透系数的增加而增加,增长的趋势逐步放缓。单侧水位降低时,降幅、降速的变化对边坡稳定性的影响更大。
(3) 当黏性土路堤堤外水位发生变化时,路堤侧向位移主要集中在路堤中部,且随着水位高度的增加而增加。路堤最大位移发生在右侧(也即背水面)坡面中下部。路堤最大位移随着水位变化向坡面下部发展,边坡变形幅度增大。当单侧水位降低时,应当注意此处加固。
(4) 研究4个因素(路堤高度、水位降幅、水位降速、渗透系数)对单侧水位变化下黏性素填土浸水路堤稳定性的影响。结果发现,针对本文中研究的具体物理力学参数填土材料:路堤高度变化对路堤稳定性的影响最大,贡献率为69.97%;渗透系数对路堤稳定性影响最小,贡献率仅为0.96%。
| [1] | RICHARDS L A. Capillary Conduction of Liquids Through Porous Mediums[J]. Journal of Applied Physics, 1931, 1 (5): 318-333 |
| [2] | ROSLAN N I, GHANI A N A, HAMID A H A. Road Subgrade Strength under Various Flooding Event[J]. Jurnal Teknologi:Sciences & Engineering, 2015, 75 (5): 39-43 |
| [3] | KANCHANA H J, PRASANNA H S. Adequacy of Seepage Analysis in Core Section of the Earthen Dam with Different Mix Proportions[J]. Aquatic Procedia, 2015 (4): 868-875 |
| [4] | 范亮. 浸水高填方路堤变形性状模型试验研究[J]. 重庆交通学院学报, 2004, 23 (6) : 78-82 FANG Liang. An Investigation of Model Test of Deformation on High Fills Embankment Soaked in Water[J]. Journal of Chongqing Jiaotong University, 2004, 23 (6): 78-82 |
| [5] | 李勇. 水位变化对浸水路堤稳定性的影响分析[J]. 交通标准化, 2007 (5) : 179-181 LI Yong. Analysis of Immerseable Embankment Stability Affected by Water Level Change[J]. Communications Standardization, 2007 (5): 179-181 |
| [6] | 贾建彬. 临河浸水路堤稳定性分析[J]. 公路交通技术, 2008 (1) : 12-14 JIA Jian-bin. Analysis of Stability of Water Immersed Road Embankment by the River[J]. Technology of Highway and Transport, 2008 (1): 12-14 |
| [7] | 楼晓昱, 曾铃. 水位升降对沿湖路基边坡渗流特征及稳定性影响的数值模拟[J]. 中外公路, 2014, 34 (2) : 31-36 LOU Xiao-yu, ZENG Ling. Numerical Simulation on Influence of Water Levels Rise and Fall of Lake on Embankment Slope Stability and Seepage Characteristics[J]. Journal of China & Foreign Highway, 2014, 34 (2): 31-36 |
| [8] | 梁燕, 李同录, 李家春, 等. 影响浸水高土石路堤稳定性因素的正交试验研究[J]. 公路, 2014 (11) : 31-35 LIANG Yan, LI Tong-lu, LI Jia-chun, et al. Orthogonal Test of Factors Affecting the Stability of High Soil-stone Embankment Immersed in Water[J]. Highway, 2014 (11): 31-35 |
| [9] | 邓学钧. 路堤路面工程[M]. 北京: 人民交通出版社, 2006. DENG Xue-jun. Embankment and Pavement Engineering[M]. Beijing: China Communications Press, 2006. |
| [10] | JTG D30-2004, 公路路基设计规范[S]. JTG D30-2004, Specifications for Design of Highway Subgrades[S]. |
| [11] | JGJ T111-1998, 建筑与市政降水工程技术规范[S]. JGJ T111-1998, Technical Code for Groundwater Lowering Engineering in Building and Municipal[S] |
 2017, Vol. 34
2017, Vol. 34
