扩展功能
文章信息
- 陈龙, 朱建勇, 何兆益, 王旭东, 张蕾
- CHEN Long, ZHU Jian-yong, HE Zhao-yi, WANG Xu-dong, ZHANG Lei
- 一种沥青混合料间断级配新型数学模型
- A New Mathematical Model for Discontinuous Gradation of Asphalt Mixture
- 公路交通科技, 2017, 34(2): 15-19, 41
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(2): 15-19, 41
- 10.3969/j.issn.1002-0268.2017.02.003
-
文章历史
- 收稿日期: 2015-11-05
2. 重庆交通大学 材料科学与工程学院, 重庆 400074;
3. 交通运输部公路科学研究院 道路结构与材料交通行业重点实验室, 北京 100088
2. School of Material Science and Engineering, Chongqing Jiaotong University, Chongqing 400074, China;
3. Key Laboratory for Road Structure & Material of Ministry of Transport, Research Institute of Highway, Ministry of Transport, Beijing 100088, China
沥青混合料级配的研究自20世纪40年代美国学者泰勒幂函数模型的提出已有70 a的历史,随后美国、前苏联以及中国的学者陆续提出Superpave法、K法及I法等级配理论[1-2]。然而上述理论均建立在级配连续性的基础上,强调混合料的整体密实。从路用性能上看,间断级配由于其良好的高温抗车辙、低温抗开裂、防水损害、抗滑耐磨以及较弱的温度敏感性,近年来得到越来越广泛的应用。沙庆林团队通过将级配曲线分为粗集料级配曲线和细集料级配曲线,设计间断型矿料级配类型,分别通过指数函数模型、幂函数模型以及对数函数模型构建代表偏粗、居中和偏细的3种级配曲线,并且通过当量粒径比Z评价级配的间断程度,取得了良好的效果[2-3]。
本文结合上述理论,在已有研究成果的基础上,提出一种沥青混合料双指标级配间断性模型计算方法,指出并改进原有3种数学函数模型下当量粒径比Z与4.75 mm通过率单因素非线性方程的不足,最后通过不同级配类型沥青混合料进行验证,发现改进后的模型比原有模型更准确。
1 原有模型介绍间断级配理论首先需要人为设置粗、细集料间断点(通常为4.75 mm),然后通过变化公称最大粒径(NMAS)通过率、0.075 mm通过率以及间断点通过率,结合上述3种函数模型,可以分别得到代表混合料级配偏粗、居中和偏细的级配曲线[4-5]。随后通过各粒级集料尺寸折中折算的方法,得到各粒级集料的代表粒径di,将其分别与对应粒级集料的分计筛余百分率ai相乘并求和即可得到该级配集料的当量粒径。譬如,若以4.75 mm为间断点,按照上述步骤分别计算粗集料的当量粒径和细集料的当量粒径,两者的比值即为当量粒径比Z,计算见式(1)。
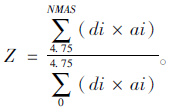
|
(1) |
本文不同类型混合料公称最大粒径通过率均假设为100%。例如,粗、细集料级配曲线均采用幂函数模型,公称最大粒径为26.5 mm,4.75 mm通过率为30%,0.075 mm通过率为5%,则当量粒径比Z的计算过程及结果如表 1所示。
| 筛孔/mm | 26.5 | 19 | 16 | 13.2 | 9.5 | 7.2 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 |
| 通过率/% | 100 | 79.2 | 70.2 | 61.4 | 48.7 | 40.1 | 30 | 22.2 | 16.4 | 12.3 | 9.1 | 6.7 | 5 |
| di/mm | 22.75 | 17.5 | 14.6 | 11.35 | 8.35 | 5.98 | 3.56 | 1.77 | 0.89 | 0.45 | 0.23 | 0.11 | 0.04 |
| ai | 0.21 | 0.09 | 0.09 | 0.13 | 0.09 | 0.10 | 0.08 | 0.06 | 0.04 | 0.03 | 0.02 | 0.02 | 0.05 |
| di×ai | 4.73 | 1.57 | 1.29 | 1.43 | 0.72 | 0.61 | 0.28 | 0.10 | 0.04 | 0.02 | 0.01 | 0.00 | 0.00 |
| Σ | 10.35 | 0.5 | |||||||||||
| Z | 23.00 | ||||||||||||
通过拟合AC,SMA,OGFC,SUPER以及AM等几种工程常用级配类型沥青混合料的当量粒径比Z与4.75 mm通过率,得到Z与4.75 mm通过率之间满足幂函数关系,其统一数学关系式见式(2)。
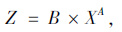
|
(2) |
式中, X为4.75 mm通过率;A,B为回归系数。
通过对不同公称最大粒径(NMAS)及0.075 mm通过率的回归系数A,B进行统计分析,得到系数A与公称最大粒径(NMAS)存在二次多项式关系,系数B与公称最大粒径(NMAS)存在线性关系,见式(3)~式(7)。
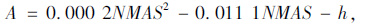
|
(3) |
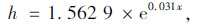
|
(4) |
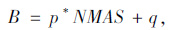
|
(5) |
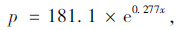
|
(6) |
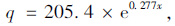
|
(7) |
式中,x为0.075 mm通过率。
将其分别代入式(2),得到当量粒径比Z与4.75 mm通过率的单因素非线性方程,见式(8)。
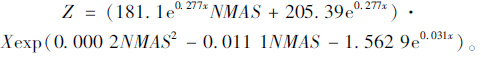
|
(8) |
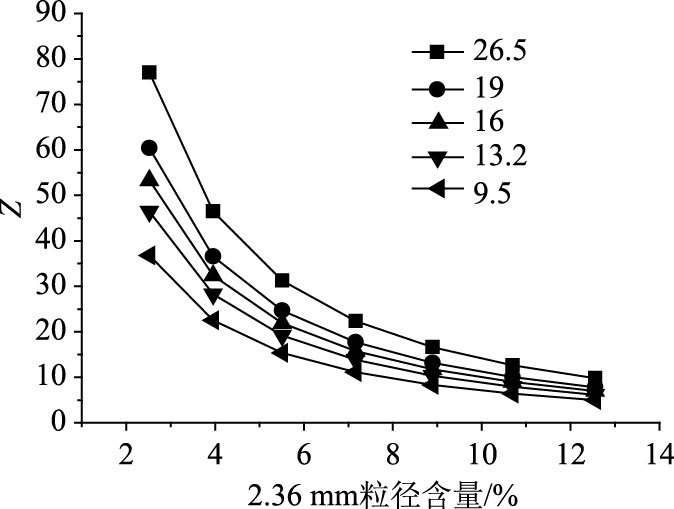
由式(1)当量粒径比Z的定义及表 1计算示例均可看出,Z的分子项主要受4.75 mm通过率的影响,该值越小,分子项的数值通常就越大;分母项不仅受4.75 mm通过率的影响,而且与2.36 mm粒径含量有很大关系。该例中,2.36 mm粒径含量占分母项的比例为0.278/0.4=70%,因此其对分母项的影响是决定性的。也就是说,当4.75 mm通过率减小时,若2.36 mm粒径含量有所增加,则分母项的数值不一定减小。由此可知,4.75 mm通过率与2.36 mm粒径含量对当量粒径比Z的影响是相互的,并且前者对Z的作用是双重的、加速的[6-7]。因此,本文参照原有模型对当量粒径比Z与2.36 mm粒径含量的统计关系进行深入研究,发现其亦符合幂函数关系[8]。以0.075 mm通过率为9%,幂函数粗集料级配举例,结果列于图 1。如无特殊说明,本文细集料级配类型均采用幂函数模型。
|
| 图 1 当量粒径比与2.36 mm粒径含量的统计关系 Fig. 1 Statistical relations between equivalent particle diameter ratio and 2.36 mm particle content |
| |
参照原有模型,建立0.075 mm通过率为5%~9%的Z与2.36 mm粒径含量的回归关系,见式(9)。
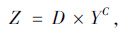
|
(9) |
式中,Y为2.36 mm粒径含量;C,D为回归系数。
根据式(9)回归关系,对不同NMAS及0.075 mm通过率的C值汇总于表 2,D值汇总于表 3。
| 0.075 mm 通过率/% | 不同最大公称粒径(mm)C值 | ||||
| 26.5 | 19 | 16 | 13.2 | 9.5 | |
| 5 | -1.350 7 | -1.337 2 | -1.328 8 | -1.318 1 | -1.300 2 |
| 6 | -1.331 9 | -1.318 9 | -1.310 8 | -1.300 6 | -1.283 4 |
| 7 | -1.313 8 | -1.301 4 | -1.293 6 | -1.283 8 | -1.267 4 |
| 8 | -1.296 2 | -1.284 3 | -1.276 9 | -1.267 5 | -1.251 8 |
| 9 | -1.278 9 | -1.267 5 | -1.260 4 | -1.251 4 | -1.236 3 |
| 0.075 mm 通过率/% | 不同最大公称粒径(mm)D值 | ||||
| 26.5 | 19 | 16 | 13.2 | 9.5 | |
| 5 | 364.25 | 279.89 | 244.21 | 209.41 | 161.67 |
| 6 | 332.95 | 256.46 | 224.10 | 192.52 | 149.10 |
| 7 | 306.87 | 236.89 | 207.28 | 178.38 | 138.55 |
| 8 | 284.57 | 220.13 | 192.86 | 166.24 | 129.47 |
| 9 | 265.13 | 205.49 | 180.25 | 155.61 | 121.51 |
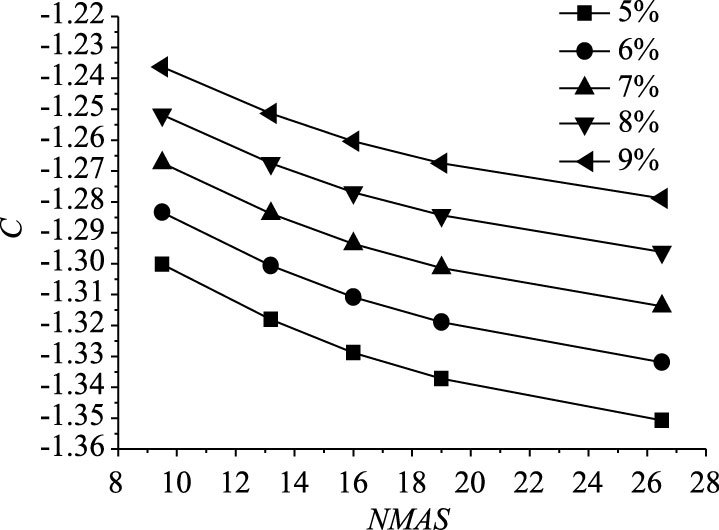
对于回归系数C,根据表 2所列数据建立公称最大粒径(NMAS)与其之间的函数曲线,见图 2所示。该函数曲线可以采用统一的二次多项式进行回归,相关系数均达到0.99以上,见式(10)所示。
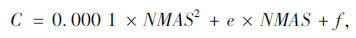
|
(10) |
式中,e,f为回归系数。
|
| 图 2 回归系数C与公称最大粒径NMAS的统计关系 Fig. 2 Statistical relations between regression coefficient C and NMAS |
| |
另外,通过分析可以得到0.075 mm通过率与e,f的统计关系式,见表 4及式(11)、式(12)所示。
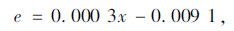
|
(11) |
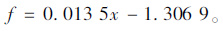
|
(12) |
| 0.075 mm 通过率/% | 9 | 8 | 7 | 6 | 5 |
| e | -0.006 4 | -0.006 7 | -0.007 0 | -0.007 3 | -0.007 6 |
| f | -1.185 3 | -1.198 7 | -1.211 9 | -1.225 4 | -1.239 6 |
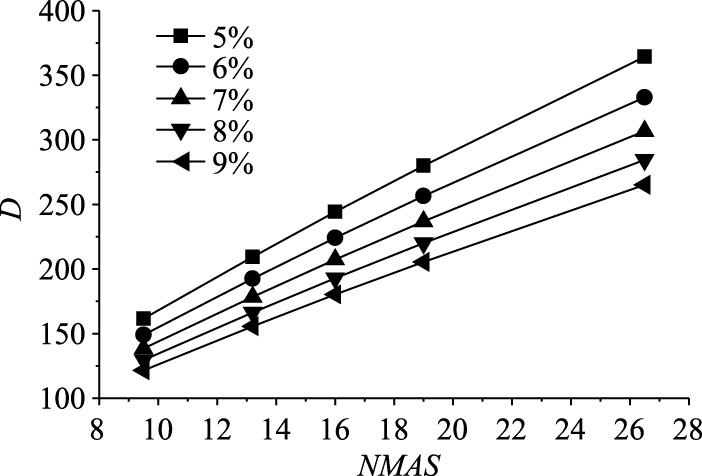
对于回归系数D,根据表 3所列数据建立公称最大粒径(NMAS)与其之间的函数曲线,见图 3所示。该函数曲线可以采用统一的线性方程进行回归,相关系数均达到0.99以上,如式(13)所示。
|
| 图 3 回归系数D与公称最大粒径NMAS的统计关系 Fig. 3 Statistical relations between regression coefficient D and NMAS |
| |
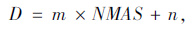
|
(13) |
式中m,n为回归系数。
同样,通过分析也可以得到0.075 mm通过率与m,n的统计关系式,如表 5及式(14)、式(15)所示。
| 0.075 mm 通过率/% | 9 | 8 | 7 | 6 | 5 |
| m | 8.42 | 9.09 | 9.87 | 10.78 | 11.88 |
| n | 43.89 | 45.60 | 47.47 | 49.55 | 51.90 |
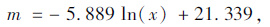
|
(14) |
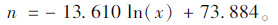
|
(15) |
综合式(9)~式(15),可得粗集料级配类型为幂函数模型时的回归关系,如式(16)所示。
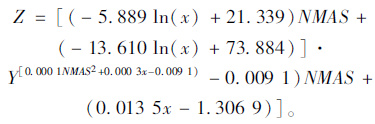
|
(16) |
根据当量粒径比Z的定义,假设分子项及分母项对其数值的影响程度均为50%。总结各函数模型,分母项中2.36 mm粒径含量所占比例在70%左右,因此4.75 mm通过率与2.36 mm粒径含量对当量粒径比Z的权重比为[50%+50%(1-70%)]:(50%×70%),即大致为60%:40%。改进后的新型级配间断性模型计算公式如式(17)所示。
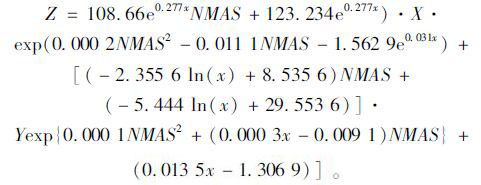
|
(17) |
参照上述分析过程,分别对其余两种数学模型-对数函数模型和指数函数模型下的级配间断性指标Z进行计算,具体过程不再详述。原有模型下的回归公式分别见式(18)~式(19),改进模型下的回归公式分别见式(20)~式(21)。
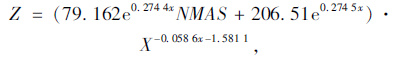
|
(18) |
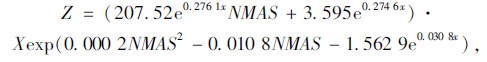
|
(19) |
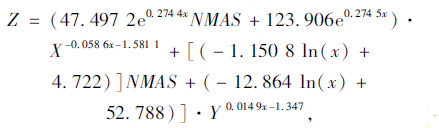
|
(20) |
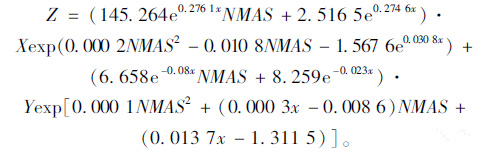
|
(21) |
通过定义式(1)、原有模型计算式(8)、(18)、(19)及改进模型计算式(17)、(20)、(21),分别对表 6所列6种工程常用级配类型沥青混合料级配范围中值的当量粒径比Z进行计算并对比,根据式(22)计算两类模型的偏差V,结果见表 7。
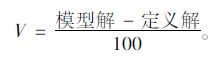
|
(22) |
| 混合料类型 | 各筛孔尺寸(mm)通过率/% | ||||||||||
| 19 | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
| AC-16 | 100 | 95 | 84 | 70 | 48 | 34 | 24.5 | 17.5 | 12.5 | 9.5 | 6 |
| SMA-16 | 100 | 95 | 75 | 55 | 26 | 19.5 | 18 | 15 | 12.5 | 11.5 | 10 |
| OGFC-16 | 100 | 95 | 80 | 57.5 | 21 | 16 | 12 | 9.5 | 7.5 | 5.5 | 4 |
| AM-16 | 100 | 95 | 72.5 | 56.5 | 29 | 15.5 | 10.5 | 7.5 | 5 | 4 | 2.5 |
| SUP-16 | 100 | 97.5 | 79 | 67 | 46 | 30 | 20 | 14 | 10 | 7 | 5 |
| SAC-16 | 100 | 97.5 | 82.5 | 62.5 | 35 | 27.5 | 21 | 16.5 | 13 | 10.5 | 8 |
| 级配 | 定义值 | 原有模型偏差 均值/% | 改进模型偏差 均值/% |
| AC-16 | 7.38 | 1.2 | 0.9 |
| SMA-16 | 26.81 | 6.4 | 3.6 |
| OGFC-16 | 28.59 | 4.9 | 3.7 |
| AM-16 | 12.98 | 2.3 | 1.7 |
| SUP-16 | 7.24 | 1.1 | 0.9 |
| SAC-16 | 15.27 | 2.5 | 1.9 |
由表 7的比对结果可知,改进后的新型级配间断性模型计算结果与定义计算结果的偏差明显比原有模型小,说明当量粒径比Z不仅受4.75 mm通过率的影响,同时也与2.36 mm粒径含量有很大关系[9-10]。本文改进的双指标级配间断性模型与原有模型相比,不仅更加符合指标Z的定义,而且计算结果也有较大改善。另外,3种函数模型下,Z值计算结果偏差大小的排序为:幂函数<指数函数<对数函数,说明粗集料采用幂函数时,当量粒径比Z的模型结合结果相对最准确[11]。但需要注意的是,本文原有模型及改进模型细集料级配曲线均是建立在幂函数模型的前提下,并没有考虑其他两种数学模型,并且结果验证涵盖了连续级配和间断级配,因此与3种数学函数模型下的理论值相比难免会有一定的偏差[12]。读者可以在本文的基础上继续开展细集料为另外两种数学模型及其组合条件下的级配间断性计算方法的研究及验证。
4 结论(1) 4.75 mm通过率和2.36 mm粒径含量分别与当量粒径比Z回归,两者回归系数的统计关系式有所不同,上述两因素之间既有联系又有差异。
(2) 4.75 mm通过率对级配间断性指标--当量粒径比Z的影响是双重、加速的。总结3种数学函数模型,4.75 mm通过率与2.36 mm粒径含量对当量粒径比Z影响的权重比为60%:40%。
(3) 提出了一种新型双指标级配间断性模型计算方法,得到3种数学函数下当量粒径比Z的计算式。与原有模型计算结果相比,新模型不仅符合该指标Z的定义,而且计算结果更加准确。这说明当量粒径比Z不仅受4.75 mm通过率的影响,同时也与2.36 mm粒径含量有很大关系。
(4) 不论原有模型还是改进模型,与定义解相比,模型解偏差大小排序为:幂函数<指数函数<对数函数。
| [1] | 王立久, 刘慧. 聚酯纤维沥青混合料级配设计的理论方法[J]. 公路交通科技, 2009, 26 (1) : 11-15 WANG Li-jiu, LIU Hui. Theoretical Method of Aggregate Grading Design of Asphalt Mixture with Polyester Fiber[J]. Journal of Highway and Transportation Research and Development, 2009, 26 (1): 11-15 |
| [2] | 王旭东, 张蕾. 基于骨架嵌挤型原理的沥青混合料均衡设计方法[M]. 北京: 人民交通出版社, 2014. WANG Xu-dong, ZHANG Lei. Multi-performance Design of Hot Mix Asphalt Based on Stone Interlock Structure Theory[M]. Beijing: China Communications Press, 2014. |
| [3] | 沙庆林. 多碎石沥青混凝土SAC系列的设计和施工[M]. 北京: 人民交通出版社, 2005. SHA Qing-lin. Design and Construction of SAC Series of Stone Asphalt Concrete[M]. Beijing: China Communi-cation Press, 2005. |
| [4] | 沈金安. 沥青及沥青混合料路用性能[M]. 北京: 人民交通出版社, 2001. SHEN Jin-an. Road Performance of Asphalt and Asphalt Mixture[M]. Beijing: China Communication Press, 2001. |
| [5] | JTG F40-2004, 公路沥青路面施工技术规范[S]. JTG F40-2004, Technical Specifications for Construction of Highway Asphalt Pavements[S]. |
| [6] | JTG D50-2006, 公路沥青路面设计规范[S]. JTG D50-2006, Specifications for Design of Highway Asphalt Pavement[S]. |
| [7] | 从卓红, 郑南翔. 沥青混合料级配优化设计[J]. 长安大学学报:自然科学版, 2007, 27 (3) : 15-19 CONG Zhuo-hong, ZHENG Nan-xiang. Optimization of HMA's gradation design[J]. Journal of Chang'an University:Natural Science Edition, 2007, 27 (3): 15-19 |
| [8] | 王立久, 刘慧. 骨架密实型沥青混合料集料级配设计方法[J]. 中国公路学报, 2008, 21 (5) : 6-9 WANG Li-jiu, LIU Hui. Method of Aggregate Gradation Design of Skeleton Denseness Asphalt Mixture[J]. China Journal of Highway and Transport, 2008, 21 (5): 6-9 |
| [9] | 赵可, 卢永贵, 魏如喜. SMA高温稳定性研究[J]. 中国公路学报, 2004, 17 (2) : 11-17 ZHAO Ke, LU Yong-gui, WEI Ru-xi. Research on High Temperature Properties of SMA[J]. China Journal of Highway and Transport, 2004, 17 (2): 11-17 |
| [10] | 马成良, 张海军, 李素平. 现代试验设计优化方法及应用[M]. 郑州: 郑州大学出版社, 2007. MA Cheng-liang, ZHANG Hai-jun, LI Su-ping. Modern Experimental Design Optimization and Application[M]. Zhengzhou: Zhengzhou University Press, 2007. |
| [11] | 陈国明, 谭忆秋, 王哲人, 等. 沥青混合料级配曲线走向的分形研究[J]. 公路交通科技, 2005, 22 (1) : 1-4 CHEN Guo-ming, TAN Yi-qiu, WANG Zhe-ren, et al. Fractal Study of Grading Curve Trend of the Asphalt Mixtures[J]. Journal of Highway and Transportation Research and Development, 2005, 22 (1): 1-4 |
| [12] | 张润初, 杜倩云, 俞祝良, 等. 一种利用参考图像与路面信息的道路监控摄像机标定方法[J]. 公路交通科技, 2014, 31 (11) : 137-141 ZHANG Run-chu, DU Qian-yun, YU Zhu-liang, et al. A Calibration Method for Road Monitoring Cameras Exploiting Reference Images and Roadway Information[J]. Journal of Highway and Transportation Research and Development, 2014, 31 (11): 137-141 |
 2017, Vol. 34
2017, Vol. 34
