扩展功能
文章信息
- 李志林, 邱红桐, 封春房, 李标
- LI Zhi-lin, QIU Hong-tong, FENG Chun-fang, LI Biao
- 基于路网分层的协同诱导路径搜索算法
- A Cooperative Guidance Path Searching Algorithm Based on Hierarchical Road Network
- 公路交通科技, 2017, 34(1): 143-148
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 143-148
- 10.3969/j.issn.1002-0268.2017.01.020
-
文章历史
- 收稿日期: 2015-06-10
2. 现代城市交通技术江苏高校协同创新中心, 江苏 南京 210096
2. Jiangsu Province Collaborative Innovation Certer of Mordeern Urban Traffie Technologies, Nanjing Jiangsu 210096, China
随着交通问题的日益严重,动态交通诱导系统作为智能运输系统的重要组成部分,逐渐受到交通管理者的青睐。动态交通诱导系统以动态交通分配理论为基础,结合路网动态信息,对道路上行驶的车辆进行路径诱导,实现行驶车辆在路网中的均衡分布,从而有效地缓解道路交通拥堵[1-2]。根据诱导路径生成方式的不同,交通诱导系统可以分为分布式路径诱导和中心式路径诱导两种方式[3-4]。
然而,在大规模路网条件下,中心式诱导方式要提供所有起讫点间的最优路径[5-6],计算时间长,影响系统的实时性能[7]。针对以上问题,吴磊[7]、江进等[8]通过车辆自组织网络中的信息交互功能进行交通状态信息采集,利用实时交通状态信息进行路径寻优,以改善系统的实时性能。于德新[8]、陆阳[9]、D. Delling等[10]通过阈值限定搜索区域和层次策略,启发式策略、数据结构化、双向搜索与并行计算等改进算法来提高搜索效率。龚勃文[11]通过大规模路网下的路网拓扑结构快速更新来实现短时内多条路径的搜索。尽管以上算法和策略在一定程度上提高了中心式诱导的实时性能,但是由于道路设施设备的限制,对中心式诱导的改善程度有限。而分布式路径诱导能在小范围内提供高质量的诱导信息[12],避免拥堵转移[13-14]的出现。
本文把城市路网中的主干道和次干道进行路网分层,利用中心式诱导的可靠预测实现主干道路网的车辆路径诱导,而分布式诱导完成对交通流局部道路和街道等路径的诱导,以期通过分布式诱导的各自车载端对所处次要路网的最优路径独立计算,减少中心式诱导的路径搜索负担,从而构建可以满足实时性要求的两种诱导方式优势互补的协同式诱导搜索算法,即通过牺牲部分最优路径的效益,而取得搜索时效性的更大效益。最后,选取厦门市厦门岛的全路网在ArcGIS上对此算法模型进行仿真验证。
1 路网 1.1 路网构建针对交通出行者路径选择偏好的相关研究,采取以下两点基本假设:(1) 当可选择路径费用无明显差异时,长距离驾驶的驾驶员更偏好于选择主要道路行驶。(2) 小区域范围内短距离行驶的驾驶员对小范围内的次要道路比较熟悉,更愿意接受出行费用相对较小的次要道路。
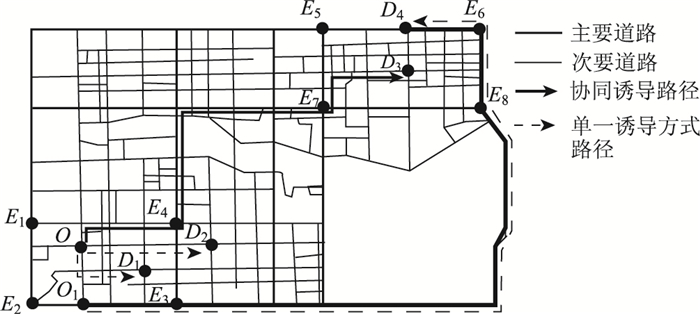
基于以上假设,同时考虑路网的连通性,本文把快速路和主干道划分为高层路网,把剩余的次干道作为低层路网。路网被主干道划分成不同的自然网格(子区域),不同的子区域由次干道、支路等一般道路组成并通过跨层节点与高层路网相连,如图 1所示。假设所研究的全路网为G=(V, A),则高层路网G1(V, A)如图 1中粗实线所示;低层路网G2i(v, a)如图 1中细实线所示(i为路网中子区域数),其中V, v表示路网中的节点集合,Ei∈V为跨层节点,表示低层路网和高层路网交接的节点,是实现两种路径对接的关键节点;A, a表示路网中的路段集合。
|
| 图 1 路网 Fig. 1 Road network |
| |
2 协同机理
在对路网进行有效分层分区的情况下,根据不同的出行起讫点,把搜索路径及所要采取的诱导方式划分为如下4类:在子区域内的出行诱导路径(如图 1中的OD1),运用分布式诱导;在相邻子区域间的出行诱导路径(如图 1中的OD2),运用分布式诱导;起讫点均在主干道上的出行路径(如图 1中的O1D4),运用中心式诱导;而起讫点在不同子区域内的远距离出行路径(如图 1中的OD3),需要把中心式诱导和分布式诱导两种方式的结果叠加在一起。因此,此协同算法将主要对如何在路径OD3中的跨层节点En处实现两种诱导方式的协同机理进行研究。
构建协同算法模型,需要选择一种高效成熟的启发式算法,A*算法通过估计函数的选择来确定路径搜索方向,是目前为止效率最高的搜索算法。所以在本文中以A*算法作为构建新的协同式算法模型和仿真验证的基础算法。
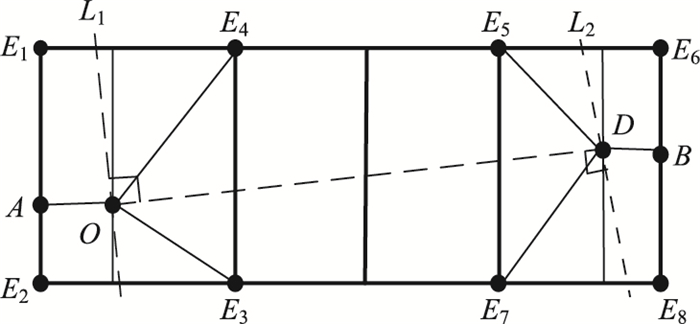
2.1 子区域动态搜索限定在图 2中,路径OD由OE4, E4E5, E5D这3部分组成,而OE4, E5D分别属于不同的子区域E1E2E3E4和E5E6E7E8,需要进行分布式诱导的路径搜索,期望路径为O→E4→E5→D。由于车载端独立于交通控制中心在相应的子区域中独立进行路径搜索,为了避免出现路径O→A→E1→E4→E5→E6→B→D等绕行路径,需要对路径搜索的范围进行限制。
|
| 图 2 搜索限制区域 Fig. 2 Restricted searching areas |
| |
为了提高路径搜索的效率和准确度,本文构造了DRSIS (Dynamic Restricted Searching in Sub-domain)方法。此方法假设起点坐标O(xO, yO)和讫点D(xD, yD)分别为边界点,作起讫点OD连线的垂直线L1⊥OD,L2⊥OD(如图 2中虚线L1,L2所示)作为所搜索区域的边界线,即两个虚线范围内的节点为本路径搜索的有效节点。
2.2 基于改进A*的跨层节点确定方法在运用DRSIS方法对子区域的搜索节点进行限定的前提下,为了进一步提高搜索的精度,采用基于改进A*的跨层节点的确定方法(Confirmation of Cross-layer Node Based on Improved A* Algorithm,COCNBIA)。其中A*算法为[15]:
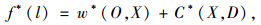
|
(1) |
式中,w*(O, X)为高层路径起点O到当前节点X的实际权值;C*(X, D)为当前节点X到目的节点D的估计函数。通过设计合适的估计函数C*(X, D)来确定跨层节点是本方法的关键。在构建估计函数时引入路径方向和节点权重两个参数,即:
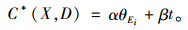
|
(2) |
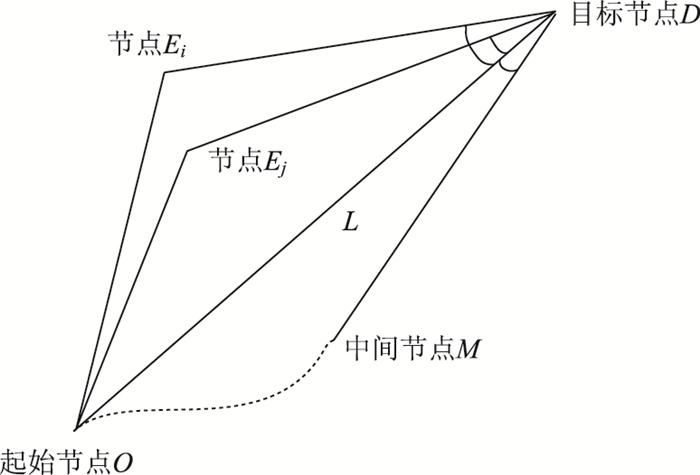
在本文中跨层节点E{Ei, Ej, …}的方向定义如下:设目的节点D与源节点O的连线OD与某跨层节点Ei的连线DEi的夹角为θEi=∠ODEi,{Ei, Ej, …}表示在路径搜索过程中,被搜索的不同跨层节点的集合,如图 3中所示(0≤∠ODEi≤π)。跨层节点E所延伸的路径的单位长度的路阻值表示为tDE(q, c, d)/LDE,其中tDE(q, c, d)是关于路段动态交通量、速度、密度等状态参数的函数。其95%置信区间为:[min{tDE(q, c, d)/LDE}, max{tDE(q, c, d)/LDE}], 其中LDE为DE两点间的欧式距离。由于两个参数的单位不一致,需要把角度和路阻进行归一化处理,即对节点E的两个参数值进行去纲量。设:
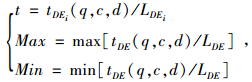
|
(3) |
则估计函数:
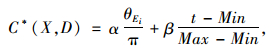
|
(4) |
式中α, β分别为两个无纲量值的加权系数,其取值范围分别为0.35~0.45,0.55~0.65。
|
| 图 3 估计函数构造图 Fig. 3 Estimate function structure diagram |
| |
3 协同诱导算法 3.1 基于COCNBIA的跨层路径搜索
在对路网进行有效分层的基础上[16],针对图 1中路径OD3所代表的跨层路径类别,提出了基于COCNBIA的跨层路径搜索算法。
输入:路网中任意两个节点O和D分别位于不同的子区域,O为起点,D为终点。
目标:搜索O和D之间的最短分层路径。
Step 1 初始化,加载O,D所在子区域的路网数据。
Step 2 车载端通过DRSIS方法确定搜索区域。在T1时刻车载机通过A*算法分别计算出OD所在子区域内的出行路径,并提供相应的跨层节点Ei,Ej。
Step 3 车载端提供行车路径OEi,OEj的同时,把Ei和Ej作为新的起讫点请求发送给中心式诱导控制中心。
Step 4 在T2时刻,中心式诱导控制中心采用A*算法在高层路网中求解最短路径EiEj,并输出给车载端。其中,为了保证在车辆进入高层路网前,可以得到有效的路径,T2需满足T2 < T1+LOEi/vOEi,其中,LOEi为路段OEi的长度,vOEi为路段OEi的区间平均速度,Ej为D所在的子区域的边界节点。
Step 5 最终由车载端的可视设备输出完整的OD路径为:OEi→EiEj→EjD。
本算法考虑了远距离出行的道路使用者偏向于选择主干道行驶,而且在不是特别绕道的情况下,会尽量避免在不同等级的道路间频繁地切换行车,即如图 1中的行驶路径。通过车载机分别计算子区域内的支路网中出行路径OEi之间总出行距离Dist (O, Ei)、EjD之间总出行距离Dist (Ej, D)和中心式诱导端提供的主干道上以有效虚拟点EiEj为起讫点的最短出行路径Dist (Ei, Ej),得到OD之间总出行费用(距离、行程时间)最小的路径LOD:
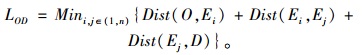
|
(4) |
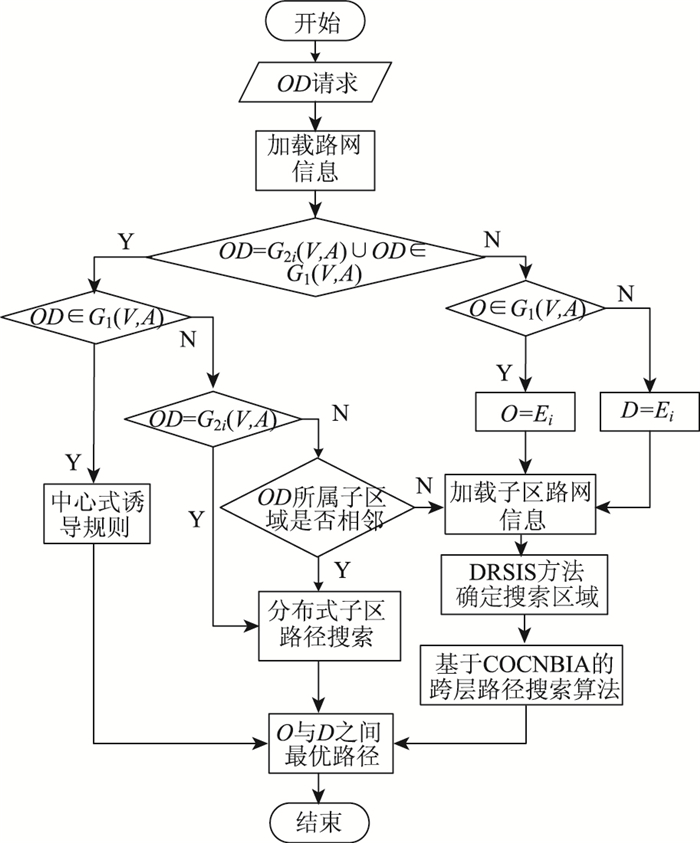
根据道路上出行者路径OD点所属路网层级的不同,构成了不同的出行路径类型,进而确定相应的诱导方式。中心式诱导实现高层路网G1(V, A)上车辆的出行诱导以及跨层路径中高层路网上的路径搜索,并可在一定程度上调整整个路网中交通流的均衡分布。而分布式诱导主要实现路径的起讫点OD在一个低层路网子区域G2i(v, a)内部或两个相邻子区域间的出行的诱导。在路网规模较大时,应采用表的形式存储数据,此时遍历效率远高于邻接矩阵的存储形式[17]。进而实现两种诱导方式的交互协同,具体的算法流程见图 4。
|
| 图 4 协同搜索算法流程 Fig. 4 Flowchart of cooperation searching algorithm |
| |
4 试验分析
为了验证本文提出的协同算法的有效性,搭建了一个以ArcGIS软件为平台的协同式路径诱导系统。在此平台上对电子地图GIS进行二次开发,实现软件后台代码与相关路网数据库相连并调用。本试验在配置为2.8 GHz双核处理器、2 GB内存、操作系统为Windows7的计算机上运行。此平台采用Client/Server模型来构建系统,主要包括两部分,分别为中心式交通信息控制中心ITSServer和分布式的车载单元ITSClient。
协同算法通过创建CLOSED表保存已被搜索的节点,OPEN表保存所有已生成但未被检索的节点。连接子层G2i=(v, a)与高层G1=(V, A)之间的节点E作为高层的起始节点Ei。遍历当前节点的各个相邻节点M,根据式(3)计算M的估价值,实现两种路径诱导方式的协同诱导。
仿真过程中,选取厦门市厦门岛的实际路网为试验路网,通过导入OD矩阵文件的形式在路网中加载了不同的路网负载(整个路网的流量加载量如图 6横坐标所示)。分别对中心式诱导和分布式诱导的运行特性,包括不同负载条件下的路网平均行程时间、OD路径的平均长度、平均费用函数、已经路径的平均计算时间等参数,并做相应分析。

|
| 图 5 路网仿真图 Fig. 5 Simulation of road network |
| |
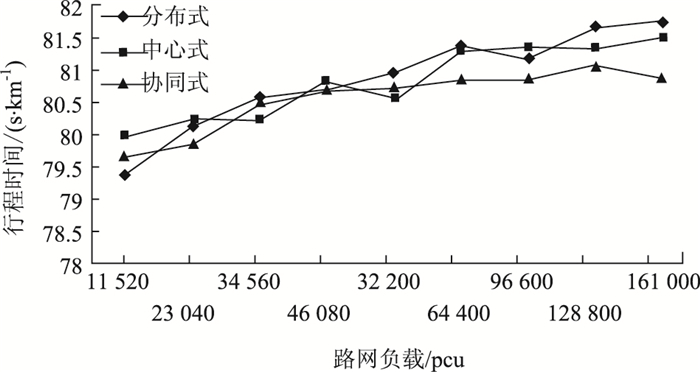
图 6对3种诱导方式的平均行程时间进行了仿真分析。在低负载情况下,分布式诱导表现出了一定的优势,但是随着路网负载的增加,协同式诱导开始优于其他两种诱导方式,并且优势越来越大。
|
| 图 6 行程时间 Fig. 6 Travel time |
| |
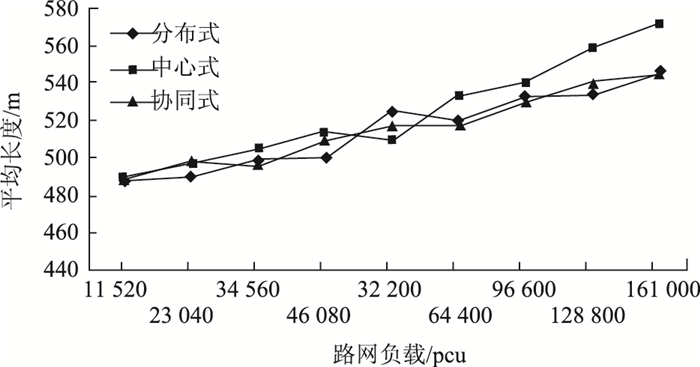
图 7对3种诱导方式生成的平均诱导路径的长度进行了分析。路网在低负载下,3种诱导方式生成的路径长度基本一样,但是随着负载增加,协同式诱导和分布式诱导提供的路径相对较短,其中分布式诱导生成的路径与其只选择最短路径行驶的特性有关,代价为拥堵转移带来的高行程时间,所以相比之下,协同式诱导效果最优。
|
| 图 7 路径平均距离 Fig. 7 Average length of path |
| |
为了更好地对比协同式路径搜索算法的综合性能,选取了路网中的4条路径,对其平均路径费用、平均等待次数、平均速度、平均延误、计算时间进行了综合统计分析,如表 1所示。由于现实中分布式诱导的计算是由车辆单独计算完成,所以表中分布式诱导的路径计算时间没有给出。可以看出,相比于其他两种诱导方式,协同式诱导表现出了一定优势。综上对比分析可得,协同式诱导搜索到的路径误差平均为2.11%,但是搜索速度快了17.5倍,所以协同式诱导在改善原有诱导方法上有很大潜力。
| 性能指标 | 平均路径费用 | 平均等待次数/次 | 平均速度/ (km·h-1) | 平均延误/s | 计算时间/s |
| 分布式 | 32.714 39 | 1.566 | 44.037 01 | 20.532 4 | - |
| 中心式 | 31.160 03 | 1.352 | 45.489 9 | 15.324 5 | 0.35 |
| 协同式 | 30.887 24 | 1.211 | 47.354 6 | 13.241 5 | 0.02 |
5 结论
本文针对现有的分布式诱导和中心式诱导存在的不足,提出了两种诱导方式优势互补的协同式诱导路径搜索算法。此算法能很好地减轻交通信息控制中心的路径计算负担,从而提高最优路径的计算效率,并能为用户提供相对高质量的出行路径。但由于要实现这两种方式的协同需要信息中心和车载端的高质量的通信技术支持,如何在通信中断或不佳的情况下运用此算法模型以及如何提高此算法搜索精度,将是下一步研究的重点。
| [1] | 杨兆升. 城市交通诱导系统理论与模型[M]. 北京: 人民交通出版社, 2000 : 12 -26. YANG Zhao-sheng. Theory and Model of Urban Traffic Guidance System[M]. Beijing: China Communications Press, 2000 : 12 -26. |
| [2] | YANG Z, MA D. Study on the Implement Technologies of Urban Traffic Flow Guidance System[C]//International Conference on Traffic and Transportation Studies. Guilin:American Society of Civil Engineers, 2002. |
| [3] | CHEN Q, STAUSS H J. Evaluating Traffic Effects of a Route Guidance System By Dynamic Simulation[J]. Simulation Practice and Theory , 1997, 5 (7/8) : 793-804 |
| [4] | ZHANG H, SUN J Q, HUI Q J, et al. Vehicle Route Optimization of Centrally Dynamic Route Guidance Systems[C]//Urban Transport XIV:Urban Transport and the Environment in the 21st Century. Malta:WIT Press, 2008. |
| [5] | BOYCE D E, LEE D H, JANSON B N, et al. Dynamic Route Choice Model of Large-scale Traffic Network[J]. Journal of Transportation Engineering , 1997, 123 (4) : 276-282 |
| [6] | O'CEARBHAILL E A, O'MAHONY M. Parallel Implementation of a Transportation Network Model[J]. Parallel and Distributed Computing , 2005, 65 (1) : 1-14 |
| [7] | 吴磊.车辆自组织网络环境下动态路径诱导系统的建模与优化策略研究[D].济南:山东大学, 2014. WU Lei. Modeling and Optimization of Dynamic Route Guidance System under Vehicular Ad-Hoc Networks[D]. Jinan:Shandong University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10422-1015532010.htm |
| [8] | 于德新, 杨兆升, 高鹏. 动态限制搜索区域的带约束K则最优路径算法[J]. 吉林大学学报:工学版 , 2009, 39 (S2) : 172-176 YU De-xin, YANG Zhao-sheng, GAO Peng. Constrained K-shortest Paths Algorithm within Dynamic Restricted Searching Area[J]. Journal of Jilin University:Engineering and Technology Edition , 2009, 39 (S2) : 172-176 |
| [9] | 陆阳, 胡坚明, 张佐, 等. 面向北京市路网特点的新型路径诱导算法及实现[J]. 交通信息与安全 , 2009, 27 (2) : 25-28 LU Yang, HU Jian-ming, ZHANG Zuo, et al. A New Route Guidance Algorithm Oriented to Beijing and Its Application[J]. Journal of Transportation Information and Safety , 2009, 27 (2) : 25-28 |
| [10] | DELLING D, SANDERS P, SCHULTES P, et al. Engineering Route Planning Algorithms, Algorithmics of Large and Complex Networks[C]//Proceedings of Algorithmics of Large and Complex Networks. Heidelberge, Germany:Springer, 2009:117-139. |
| [11] | 龚勃文.大规模路网下中心式动态交通诱导系统关键技术研究[D].长春:吉林大学, 2010. GONG Bo-wen. Research on Key Technologies of Centrally Dynamic Traffic Flow Guidance System under Large-scale Network[D].Changchun:Jilin University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10183-2010107425.htm |
| [12] | 秦进, 史峰, 侯桂荣.基于车辆的混合式路径诱导系统[C]//第二十七届中国控制会议论文集.昆明:中国自动化学会, 2008. QIN Jin, SHI Feng, HOU Gui-rong, Vehicle-based Hybrid Route Guidance System[C]//Proceedings of the 27th Chinese Control Conference. Kunming:Chinese Association of Automation, 2008. |
| [13] | BAZZAN A L C, KLUGL F. Case Studies on the Braess Paradox:Simulating Route Recommendation and Learning in Abstract and Microscopic Models[J]. Transportation Research Part C:Emerging Technologies , 2005, 13 (4) : 299-319 |
| [14] | RILETT L R, VAN AERDE M W. Modelling Distributed Real-time Route Guidance Strategies in a Traffic Network That Exhibits the Braess Paradox[C]//Vehicle Navigation and Information Systems Conference. Dearborn, US:SAE, 1991. |
| [15] | 葛艳, 王健, 孟友新, 等. 车辆导航动态路径规划的研究进展[J]. 公路交通科技 , 2010, 27 (11) : 113-117 GE Yan, WANG Jian, MENG You-xin, et al. Research Progress on Dynamic Route Planning of Vehicle Navigation[J]. Journal of Highway and Transportation Research and Development , 2010, 27 (11) : 113-117 |
| [16] | CHOU Y L, ROMEIJN H E, SMITH R L. Approximating Shortest Paths in Large-scale Networks with an Application to Intelligent Transportation[J]. Informs Journal on Computing , 1998, 10 (2) : 163-179 |
| [17] | 郑四发, 曹剑东, 连小珉. 复杂路网下多客户间最短路径的扇面Dijkstra算法[J]. 清华大学学报:自然科学版 , 2009, 49 (11) : 1834-1837 ZHENG Si-fa, CAO Jian-dong, LIAN Xiao-min. Sector Dijkstra Algorithm for Shortest Routes between Customers in Complex Road Networks[J]. Journal of Tsinghua University , 2009, 49 (11) : 1834-1837 |
 2017, Vol. 34
2017, Vol. 34
