扩展功能
文章信息
- 邵孜科, 李文权, 孙春洋, 于乐乐, 刘娟
- SHAO Zi-ke, LI Wen-quan, SUN Chun-yang, YU Le-le, LIU Juan
- 基于蒙特卡罗模拟的平行式加速车道长度模型
- A Model of Parallel Type Acceleration Lane Length Based on Monte Carlo Simulation
- 公路交通科技, 2017, 34(1): 137-142, 148
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 137-142, 148
- 10.3969/j.issn.1002-0268.2017.01.019
-
文章历史
- 收稿日期: 2015-12-30
加速车道是城市快速路或高速公路的重要组成部分,合流车辆在加速车道上完成加速和汇入过程,实现与主线的合流。如果加速车道过短,则合流车辆无法达到最佳汇入条件,合流车辆不得不强行汇入,干扰主线交通,甚至引起交通事故,或者合流车辆不得不在加速车道上等待汇入;如果加速车道过长,则造成资源浪费和建设成本增加。
我国现行规范[1-2]主要借鉴国外规范加速车道长度并结合实际经验给出推荐值,主要考虑主线速度和合流车辆的初始速度,未考虑合流车辆加速完成后的汇入过程。李铁柱[3]、李文权[4-5]等介绍了合流区的交通特性。邵长桥[6]、徐秋实[7]、慈玉生[8]、王春娥[9]等考虑了汇入过程,将平均等待时间期望内合流车辆行驶的距离作为汇入段长度。石小法[10]、邢小亮[11]、谭云龙[12]、苑中丹[13]等考虑了汇入过程,将累计汇入概率达到一定阈值条件的长度确定为汇入段长度。刘兆斌[14]、罗京等[15]则通过仿真软件直接获取加速车道长度。
上述文献计算加速车道长度虽然较多涉及了汇入过程,但在建模时多从静态角度出发,没有考虑加速过程结束后汇入过程仍是一个小范围的可变动态过程,如:如果汇入间隙在合流车辆前方,那么车辆可能会再次加速至最大合流速度以尽快完成合流;如果汇入间隙在合流车辆后方,那么车辆可能会选择减速至最小合流速度以尽快完成合流。同时,上述文献还忽略了汇入过程中的一些随机特性。本文在考虑道路运行和设计属性、驾驶员属性、车辆属性及汇入过程随机属性的基础上,提出一种基于动态汇入过程的加速车道长度计算模型,借助MATLAB软件,通过蒙特卡罗模拟实现模型的求解。
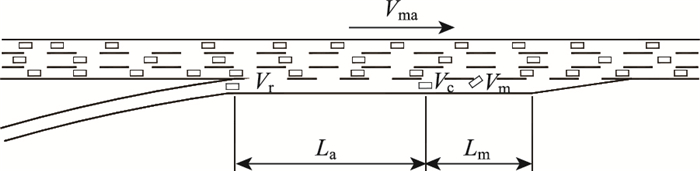
1 合流车辆合流过程分析合流车辆汇入主线可以分为加速过程和汇入过程,如图 1所示。合流车辆在加速过程中,速度由初始速度Vr加速到可以汇入主线的合流速度Vc,该过程车辆经过的长度称为加速车道的加速段长度La;合流车辆完成加速过程后,会寻找主线的可汇入间隙,当主线出现可汇入间隙时,车辆则会汇入主线,该过程车辆经过的长度称为加速车道的汇入段长度Lm。所以加速车道长度L的计算公式为:
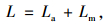
|
(1) |
式中,L为加速车道长度;La为加速车道加速段长度;Lm为加速车道汇入段长度。
|
| 图 1 车辆合流过程示意图 Fig. 1 Schematic diagram of vehicle merging process 注:本文研究的加速车道为平行式加速车道,且加速车道长度不含渐变段。 |
| |
2 加速车道长度模型 2.1 基本假设
为简化分析难度,将合流区复杂的交通状态假设成一种较为理想的状态,有3点重要的理想化假设:
(1) 如果主线车辆车头时距大于临界间隙tc,那么合流车辆就一定在该间隙内完成汇入。临界间隙tc为:
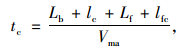
|
(2) |
式中,tc为临界车头间隙时距;Lb为合流车辆汇入时与后车的临界间距;lc为合流车辆长度;Lf为合流车辆汇入时与前车的临界间距;lfc为汇入主线间隙的前车车辆长度;Vma为主线车流速度。
(2) 合流车辆在汇入过程中,如果需要进行加速,那么合流车辆先匀加速至最大合流速度。当加速结束时,如果合流车辆仍未达到汇入条件,那么合流车辆按最大合流速度继续行驶。
(3) 合流车辆在汇入过程中,如果需要进行减速,那么合流车辆先匀减速至最小合流速度。当减速结束时,如果合流车辆仍未达到汇入条件,那么合流车辆按最小合流速度继续行驶。
本文假设车辆合流速度取值是一个区间,即认为合流车辆完成加速过程后达到的合流速度Vc具有一定随机性:

|
(3) |
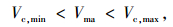
|
(4) |
式中,Vc为可汇入主线的合流速度;Vc, min为合流车辆最小合流速度;Vc, max为合流车辆最大合流速度。
2.2 加速段长度计算模型加速段长度La可以根据下式计算得出:
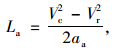
|
(5) |
式中,Vr为初始速度; aa为车辆加速度。
2.3 汇入段长度计算模型合流车辆完成加速过程后,可能出现两种情况:一是相邻主线车头时距hd不小于临界间隙tc,根据假设,车辆一定会在该间隙完成汇入;二是相邻主线车头时距hd小于临界间隙tc,此时合流车辆无法在相邻间隙完成汇入,驾驶员会在相邻间隙前方和后方寻找可汇入间隙,本文认为驾驶员将向耗时少的方向汇入。
2.3.1 合流车辆在相邻间隙完成汇入合流车辆是否需要调整相对位置完成汇入,可以分成3种情况(图 2):
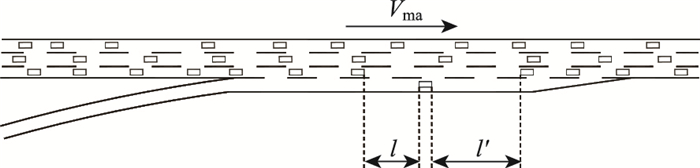
|
| 图 2 合流车辆和主线相邻间隙的后车与前车关系示意图 Fig. 2 Schematic diagram of relationship between merging vehicle with lead and lag vehicles in adjacent gap of main line |
| |
(1) 合流车辆可以直接完成汇入
此时,合流车辆和后车距离l大于临界后车间距Lb,合流车辆和前车距离l′大于临界前车间距Lf,所以
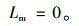
|
(6) |
(2) 合流车辆相对向后移动完成汇入
此时,合流车辆和后车距离l大于临界后车间距Lb,而合流车辆和前车距离l′小于临界前车间距Lf,合流车辆与前车距离过近,合流车辆至少需要相对向后移动距离ΔS1:
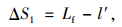
|
(7) |
式中,ΔS1为合流车相对于前车的后退距离; l′为合流车辆完成加速时与前车的距离。
为了尽快完成汇入,假设合流车辆会从合流速度Vc减速到最小合流速度Vc, min,则当整个减速过程结束时,合流车辆与主线前车的相对移动距离可通过式(8)~(11)计算:
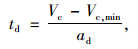
|
(8) |
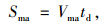
|
(9) |
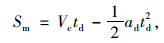
|
(10) |
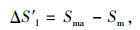
|
(11) |
式中,td为减速过程时间;ad为车辆减速加速度;Sma为td时间内前车前进距离;Sm为td时间内合流车辆前进距离;ΔS′1为td时间内前车相对合流车辆的前进距离。
根据是否在减速过程中完成汇入,可能会出现两种情况:
①合流车辆在减速过程中完成汇入
此时,ΔS1≤ΔS′1,汇入段长度Lm可按式(11)~(12)计算:
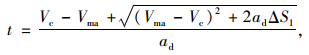
|
(12) |
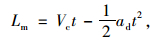
|
(13) |
式中t为达到汇入条件经过的时间。
②合流车辆在减速过程后完成汇入
此时,ΔS1>ΔS′1,合流车辆减速到Vc, min后,仍需在加速车道上行驶一段时间,然后才可汇入,汇入段长度Lm可按下式计算:
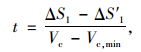
|
(14) |
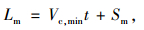
|
(15) |
式中t为减速过程完成后达到汇入条件还需要的时间。
(3) 合流车辆相对向前移动完成汇入
此时,合流车辆和后车距离l小于临界后车间距Lb,而合流车辆和前车距离l′大于临界前车间距Lf,合流车辆与后车距离过近,合流车辆至少相对向前移动距离ΔS2:
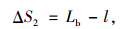
|
(16) |
式中,ΔS2为合流车相对于后车的前进距离;l为合流车辆完成加速时与后车的距离。
为了尽快完成汇入,假设合流车辆会从合流速度Vc加速到最大合流速度Vc, max,则当整个加速过程结束时,合流车辆与主线后车的相对移动距离可通过式(17)~(20)计算:
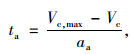
|
(17) |
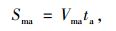
|
(18) |
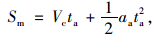
|
(19) |
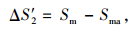
|
(20) |
式中,ta为加速过程时间;Sma为ta时间内前车前进距离;Sm为ta时间内合流车辆前进距离;ΔS′2为ta时间内前车相对合流车辆的前进距离。
根据是否在加速过程中完成汇入,可能会出现两种情况:
①合流车辆在加速过程中完成汇入
此时,ΔS2≤ΔS′2,汇入段长度Lm可按式(21)~(22)计算:
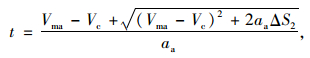
|
(21) |
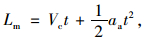
|
(22) |
式中t为达到汇入条件经过的时间。
②合流车辆在加速过程后完成汇入
此时,ΔS2>ΔS′2,合流车辆加速到Vc, max后,仍需在加速车道上行驶一段时间,然后才可汇入,汇入段长度Lm可按式(23)~(24)计算:
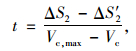
|
(23) |
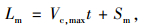
|
(24) |
式中t为加速过程完成后达到汇入条件还需的时间。
2.3.2 合流车辆不在相邻间隙完成汇入合流车辆会选择耗时少的前方或后方可汇入间隙选择汇入。
(1) 合流车辆在后方间隙汇入
合流车辆将相对向后行驶,假设后方第j间隙为可汇入间隙,于是合流车相对移动距离ΔS1为:
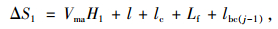
|
(25) |
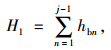
|
(26) |
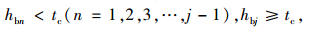
|
(27) |
式中,lbc (j-1)为后方可汇入间隙前车车辆长度;H1为累计车头时距;hbn(n=1, 2, 3,…, j)为车头时距。
为了尽快完成汇入,假设合流车辆会从合流速度Vc减速到最小合流速度Vc, min。于是,该过程转变为2.3.1节(2)类情况,按照式(8)~(11)计算出td,Sm,Sma,ΔS′1。根据是否在减速过程中完成汇入,可能会出现两种情况:
①合流车辆在减速过程中完成汇入
汇入段长度Lm可按式(28)~(30)计算:
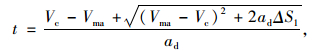
|
(28) |
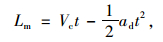
|
(29) |
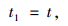
|
(30) |
式中,t为达到汇入条件经过的时间;t1为汇入过程所需的时间。
②合流车辆在减速过程后完成汇入
汇入段长度Lm可按式(31)~(33)计算:
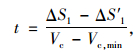
|
(31) |
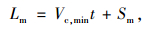
|
(32) |

|
(33) |
式中,t为减速过程完成后达到汇入条件还需要的时间;t1为汇入过程所需时间。
(2) 合流车辆在前方间隙汇入
合流车辆将相对向前行驶,假设前方第i间隙为可汇入间隙,于是合流车相对移动距离ΔS2为:
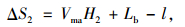
|
(34) |
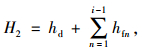
|
(35) |
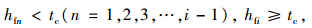
|
(36) |
式中,H2为累计车头时距;hd为相邻主线车头时距;hfn(n=1, 2, 3, …, i)为车头时距。
为了尽快完成汇入,假设车辆会从合流速度Vc加速到最大合流速度Vc, max,则该过程转变为2.3.1节(3)类情况,按照式(17)~(20)计算出ta,Sm,Sma,ΔS′2。根据是否在加速过程中完成汇入,可能会出现两种情况:
①合流车辆在加速过程中完成汇入
汇入段长度Lm可按式(37)~(39)计算:
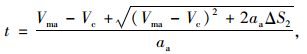
|
(37) |
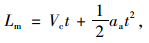
|
(38) |

|
(39) |
式中,t为达到汇入条件经过的时间;t2为汇入过程所需的时间。
②合流车辆在加速过程后完成汇入
汇入段长度Lm可按式(40)~(42)计算:
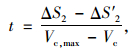
|
(40) |
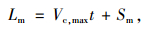
|
(41) |
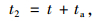
|
(42) |
式中,t为加速过程完成后达到汇入条件还需要的时间;t2为汇入过程所需时间。
(3) 合流车辆最终汇入方向确定
合流车辆最终向耗时少的方向汇入,于是有:
如果t2>t1,那么合流车辆向后方汇入;如果t2 < t1,那么合流车辆向前方汇入;如果t2=t1,那么合流车辆向任意方向汇入。
3 模型分析与算法实现 3.1 模型分析本文提出的加速车道长度模型是在考虑了道路运行和设计属性、驾驶员属性、车辆属性及汇入过程随机属性的基础上,根据合流车辆动态汇入过程分析建立的。
| 属性 | 运行和设计属性 | 驾驶员属性 | 车辆属性 | 汇入过程随机属性 |
| 参数 | Vma,Vr,q,车头时距分布 | Lb,Lf,Vc, min,Vc, max | aa,ad,各种车辆长度 | hd,i, j, l,Vc |
假设主线车头时距分布为F(h),则h≥tc的概率为p=P(h≥tc)。所以,hd≥tc的概率为p,hd≤tc的概率为1-p;前方第i间隙可以汇入的概率和后方第j间隙可以汇入的概率为:
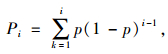
|
(43) |
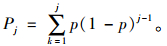
|
(44) |
合流车辆汇入时到后车的距离l与hd和Vma相关,l在(0, Vmahd]上服从均布分布,即随机变量l的密度函数为:
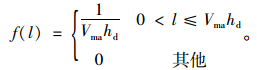
|
(45) |
汇入时合流速度Vc跟Vma,Vc, min,Vc, max相关,Vc-Vma可以认为服从某一分布,如果没有特别说明,可以假设服从正态分布,于是有:
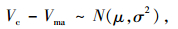
|
(46) |
式中,μ为正态分布均值;σ2为正态分布方差。
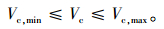
|
(47) |
对不同地区、不同环境或不同时间点,道路运行和设计属性、驾驶员属性、车辆属性和汇入过程随机属性都不尽相同。
上述建立的模型是一个概率模型,用传统的数学方法无法轻易得到模型解,蒙特卡罗模拟方法是处理概率模型的经典方法,通过生成用以表征概率模型中概率事件的随机数,进行大量的模拟试验,采用统计抽样的思想得到模型的近似解。
对建立的模型进行多次蒙特卡罗模拟,将合适百分位数的长度确定为加速车道长度。该模型假设合流车辆先加速,当速度达到要求后再寻找满足要求的间隙汇入,并假设临界汇入间隙为一固定值,不会发生变化。这两项假设都是保守型假设,可能导致最终的模型过于保守,所以合适百分位数的选取至关重要,可能低于最常用的85百分位,用以缓和过于保守模型带来的影响。
3.2 模型算法实现通过蒙特卡罗仿真模拟获取加速车道长度的主要步骤为:
步骤1:标定模型涉及到的道路运行和设计属性、驾驶员属性和车辆属性参数;
步骤2:借助MATLAB确定能够表征汇入过程随机属性的随机数形式;
步骤3:确定蒙特卡罗模拟次数M,进行模拟,获取M个加速车道的长度L;
步骤4:根据实际情况,将第α分位的长度Lα确定为加速车道长度;
步骤5:对Lα进行修正。
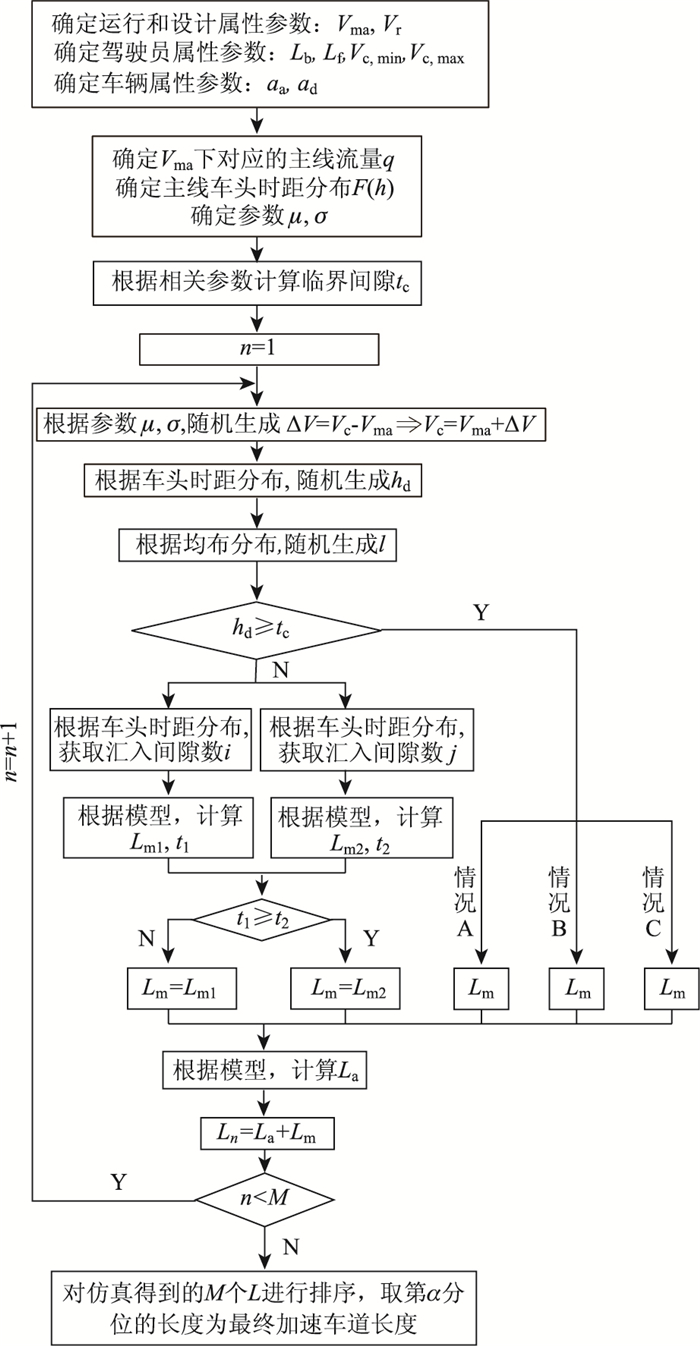
|
| 图 3 平行式加速车道长度蒙特卡罗模拟流程图 Fig. 3 Flowchart of Monte Carlo simulation for parallel type acceleration lane length |
| |
4 案例分析
某地区需要新建一条设计时速为100 km/h的快速路,匝道设计时速为30 km/h。经过分析,该快速路合流区的车辆车头时距可能服从二阶爱尔朗分布;Lb=9 m,Lf=9 m,Vc, min=Vma-3,Vc, max=Vma+2,Vc-Vma~N(-0.1, 2);aa=1 m/s2,ad=1 m/s2,车辆长度为6 m,试计算合流区加速车道长度。
根据《城市快速路设计规程》,快速路按三级服务水平设计,设计时速为100 km/h的快速路三级服务水平上限速度为76 km/h,对应的交通量为1 500 pcu/h,三级服务水平下限速度为62 km/h,对应的交通量为2 000 pcu/h。所以分Vma=76 km/h和Vma=62 km/h进行计算。在进行蒙特卡罗模拟时,仿真次数M=5 000,并进行5组仿真。
根据仿真结果,规范推荐值远小于仿真值。若设计人员将80百分位长度值作为加速度长度设计值,则加速车道设计长度为340~375 m。
| 组号 | 修正值 | ||||||
| 1 | 2 | 3 | 4 | 5 | |||
| 百分位数 | 50 | 276.98 | 276.90 | 276.45 | 267.87 | 278.30 | 275 |
| 55 | 292.47 | 295.47 | 294.36 | 286.44 | 294.39 | 295 | |
| 60 | 309.10 | 310.70 | 311.94 | 303.16 | 310.68 | 310 | |
| 65 | 323.80 | 325.12 | 326.54 | 319.59 | 325.62 | 325 | |
| 70 | 338.61 | 340.45 | 340.86 | 334.50 | 339.88 | 340 | |
| 75 | 354.85 | 356.10 | 356.12 | 351.34 | 356.51 | 355 | |
| 80 | 373.28 | 375.34 | 373.50 | 370.54 | 378.11 | 375 | |
| 85 | 395.09 | 397.16 | 395.96 | 394.72 | 400.66 | 400 | |
| 90 | 421.73 | 423.10 | 426.22 | 422.65 | 428.18 | 425 | |
| 95 | 473.51 | 470.60 | 476.15 | 472.84 | 473.51 | 475 | |
| 规范推荐值 | 180 | ||||||
| 组号 | 修正值 | ||||||
| 1 | 2 | 3 | 4 | 5 | |||
| 百分位数 | 50 | 241.65 | 241.38 | 240.09 | 240.07 | 240.37 | 240 |
| 55 | 253.38 | 253.49 | 252.69 | 252.24 | 252.22 | 255 | |
| 60 | 265.57 | 265.44 | 265.23 | 263.85 | 265.90 | 265 | |
| 65 | 279.26 | 280.39 | 279.10 | 277.45 | 281.44 | 280 | |
| 70 | 294.56 | 294.82 | 294.37 | 294.98 | 297.81 | 295 | |
| 75 | 312.35 | 312.28 | 314.19 | 313.37 | 316.43 | 315 | |
| 80 | 336.78 | 337.54 | 336.84 | 335.24 | 340.64 | 340 | |
| 85 | 368.79 | 368.80 | 368.55 | 362.25 | 371.05 | 370 | |
| 90 | 411.71 | 410.39 | 416.88 | 404.06 | 417.31 | 415 | |
| 95 | 496.11 | 484.40 | 495.52 | 474.35 | 494.27 | 495 | |
| 规范推荐值 | 180 | ||||||
5 结论
本文以合流车辆汇入过程的随机属性为突破口,考虑道路运行和设计属性、驾驶员属性及车辆属性,建立了加速车道长度模型,借助MATLAB软件,通过蒙特卡罗模拟方法给出了模型的求解方式。
通过案例分析,发现规范所规定的加速车道长度值偏短,可以根据本文建立的模型进行不同属性组合搭配,仿真模拟不同条件下的加速车道长度。
本文的模型是在较为理想状态下建立的,模型可能过于保守,所以相适宜的百分位数选取至关重要。另外,在实际运行中,汇入临界间隙的变化、匝道车流量、主线车道数等都会对模型产生影响,所以这些方面值得进一步研究。
| [1] | JTG D20-2006, 公路路线设计规范[S]. JTG D20-2006, Design Specification for Highway Alignment[S]. |
| [2] | CJJ129-2009, 城市快速路设计规程[S]. CJJ129-2009, Specification for Design of Urban Expressway[S]. |
| [3] | 李铁柱, 李文权, 周荣贵, 等. 高速公路加减速车道合流分流特征分析[J]. 公路交通科技 , 2001, 18 (4) : 89-91 LI Tie-Zhu, LI Wen-quan, ZHOU Rong-gui, et al. Traffic Characteristics Analysis for Merging and Diverging in Acceleration and Deceleration Lane of Expressway[J]. Journal of Highway and Transportation Research and Development , 2001, 18 (4) : 89-91 |
| [4] | 李文权, 王炜, 周荣贵. 高速公路合流区1车道车头时距分布特征[J]. 公路交通科技 , 2003, 20 (1) : 114-117 LI Wen-quan, WANG Wei, ZHOU Rong-gui. Headway Characteristics of Iane 1 on Expressway Merge Area[J]. Journal of Highway and Transportation Research and Development , 2003, 20 (1) : 114-117 |
| [5] | 李文权, 周荣贵. 高速公路合流区1车道交通量模型[J]. 公路交通科技 , 2004, 21 (12) : 76-79 LI Wen-quan, ZHOU Rong-gui. Traffic Flow Rate Model of Lane 1 on Expressway Merge Area[J]. Journal of Highway and Transportation Research and Development , 2004, 21 (12) : 76-79 |
| [6] | 邵长桥, 杨振海, 陈金川, 等. 一种确定加速车道长度的概率统计模型[J]. 数理统计与管理 , 2004, 20 (4) : 42-45 SHAO Chang-qiao, YANG Zhen-hai, CHEN Jin-chuan, et al. A Probability Model for Length of Acceleration Lanes on Expressway[J]. Application of Statistics and Management , 2004, 20 (4) : 42-45 |
| [7] | 徐秋实, 任福田, 孙小端, 等. 高速公路互通式立交加速车道长度的研究[J]. 北京工业大学学报 , 2007, 33 (3) : 298-301 XUN Qiu-shi, REN Fu-tian, SUN Xiao-duan, et al. Research on the Length of Acceleration Lane at Freeway Interchange[J]. Journal of Beijing University of Technology , 2007, 33 (3) : 298-301 |
| [8] | 慈玉生.快速路匝道连接段通行能力与匝道设置研究[D].哈尔滨:哈尔滨工业大学, 2008. CI Yu-sheng. On-off Ramp Junction Capacity and Ramp Setting on Urban Expressway[D]. Harbin:Harbin Institute of Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10213-2009223936.htm |
| [9] | 王春娥. 高速公路立交变速车道长度研究[J]. 公路交通科技 , 2013, 30 (1) : 120-125 WANG Chun-e. Length of Speed-change Lane at Highway Interchange[J]. Journal of Highway and Transportation Research and Development , 2013, 30 (1) : 120-125 |
| [10] | 石小法, 李文权, 李铁柱, 等. 高速公路互通立交加速车道长度的设计方法[J]. 河南大学学报:自然科学版 , 2000, 30 (4) : 17-20 SHI Xiao-fa, LI Wen-quan, LI Tie-zhu, et al. Method of Designing Acceleration Lane Length in Freeway Interchange[J]. Journal of Henan University:Natural Science Edition , 2000, 30 (4) : 17-20 |
| [11] | 邢小亮.高速公路变速车道长度研究[D].西安:长安大学, 2013. XING Xiao-liang. Research on Length of Speed Change Lane of Expressway[D]. Xi'an:Chang'an University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-11941-1014022832.htm |
| [12] | 谭云龙.快速路合流区微观交通仿真车道变换模型研究[D].长春:吉林大学, 2014. TAN Yun-Long. Study on Lane-changing Model for Expressway Weaving Area in Microscopic Traffic Simulation[D]. Changchun:Jilin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10183-1014211549.htm |
| [13] | 苑中丹, 薛岭, 王维礼. 高速公路枢纽互通式立交变速车道长度设计研究[J]. 重庆交通大学学报:自然科学版 , 2009, 28 (4) : 689-693 YUAN Zhong-dan, XUE Ling, WANG Wei-li. Length Design of Speed Change Lane at Interchanges of Expressway[J]. Journal of Chongqing Jiaotong University:Natural Science Editon , 2009, 28 (4) : 689-693 |
| [14] | 刘兆斌.高速公路加、减速车道设计标准研究[D].南京:东南大学, 2001. LIU Zhao-bin. Research on Acceleration and Deceleration Lanes Design Standard[D]. Nanjing:Southeast University, 2001. http://d.wanfangdata.com.cn/Thesis/Y413493 |
| [15] | 罗京, 谭云龙, 韩印. 快速路合流区加速车道长度设置方法研究[J]. 计算机工程与应用 , 2015 (9) : 248-251 LUO Jing, TAN Yun-Long, HAN Yin. Length Design Method of Acceleration Lane on Expressway Weaving Area[J]. Computer Engineering and Applications , 2015 (9) : 248-251 |
 2017, Vol. 34
2017, Vol. 34
