扩展功能
文章信息
- 韩志聪, 樊彦国, 吴会胜, 刘惠燕
- HAN Zhi-cong, FAN Yan-guo, WU Hui-sheng, LIU Hui-yan
- 基于GA-SVR模型的短期交通流量预测方法研究
- Study on Methods of Short-time Traffic Volume Forecasting Based on GA-SVR model
- 公路交通科技, 2017, 34(1): 130-136
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 130-136
- 10.3969/j.issn.1002-0268.2017.01.018
-
文章历史
- 收稿日期: 2016-02-24
2. 青岛市黄岛区国土资源和房屋管理局, 山东 青岛 266555
2. Land Resources and Housing Authority of Huangdao District, Qingdao Shandong 266555, China
城市化进程的推进、人类移动性的增强以及物资交流的加速促使交通运输投资越来越大,基础设施的扩建滞后于机动车辆的剧增所造成的交通堵塞、交通事故、环境污染等问题,两者之间的矛盾已成为全球性的挑战。综合利用先进的信息技术如通讯技术、计算机技术以及3S技术等是解决现有城市交通问题的有效途径之一。智能交通系统(Intelligent Transport Systems, ITS)以及交通地理信息系统(Geographic Information System-Transport, GIS-T)一直致力于交通运输效率的提高[1]。交通流量是智能交通实施的基础数据之一,科学高效的交通流量预测是实现交通规划和交通诱导的前提[2-3]。
由于短期交通流量具有不确定性强和规律性弱等特点,目前国内外学者提出的预测模型已达到几十种,根据其原理不同可分为两类:一类基于数学模型方法,如ARIMA模型[4]、卡尔曼滤波模型[5-7]、指数平滑模型[8-9]等;另一类为非数学模型方法,如神经网络[10-11]、支持向量回归[12-13]、非参数回归[14-15]等模型。数学模型预测方法在构建和求解交通流模型过程中比较困难,难以满足短时预测的需要[16],而非数学模型仅需要足够的历史数据,不需要构造复杂的交通流模型,并且预测精度也能满足ITS和GIS-T的需要。
相比其他非数学模型,支持向量回归(Support Vector Regression, SVR)在小样本、高维和非线性数据空间计算中具有很好的推广能力,并且得到的解为全局最优。因此SVR在短期交通流预测方面更具优势,能够最大限度地挖掘隐含于交通流历史数据中的信息,但其选择参数的依赖性较大。遗传算法(Genetic Algorithm,GA)具有群体搜索和内在启发式随机搜索的特性,不易陷入局部最优, 其固有的并行性和并行计算的能力非常适用于大规模并行计算[17]。鉴于此,本文将遗传算法与支持向量回归算法相结合,利用GA寻优的优势得到SVR模型中的关键参数,进而得到精确的短期交通流预测结果;另一创新点为依据获取的大量交通数据,根据不同时间周期对数据进行分类,确定最优的预测数据组合,验证GA-SVR模型的精度。
1 SVR原理SVR的基本思想是通过一个非线性映射函数φ(x)将数值映射到高维特征空间Rh,并在该空间进行线性回归[10],形成Rh下的最优决策函数f(x),其最大优点是能够有效地克服维数过高带来的计算问题和局部极值问题。其最优决策函数为:
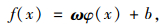
|
(1) |
式中, ω为权值向量; φ(x)为非线性映射函数; b为阈值。
为了使SVR具有较好的稀疏性,引入不敏感损失函数ε,得到损失函数:
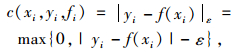
|
(2) |
即若xi的观测值yi与预测值f(xi)的差别小于ε时,损失值为0。
SVR实质上是求解式(1)中的ω和b,并且为了保证式(1)平坦,在满足ε的条件下,必须使得ω最小,即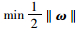
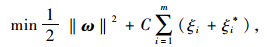
|
(3) |
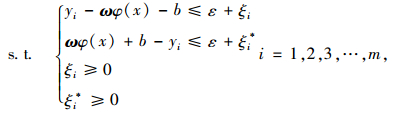
|
(4) |
式中,yi为观测值;ω为权值向量;ε为不敏感损失函数;C为惩罚参数;ξi和ξi*为松弛变量;m为样本数。
采用对偶原理将式(3)转化为二次规划问题并建立拉格朗日方程[18]:
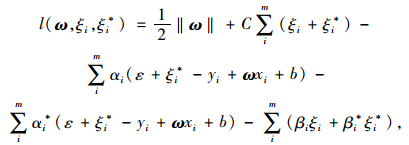
|
(5) |
式中, l(ω, ξi, ξi*)为拉格朗日方程的对偶形式; ω为权值向量; ξi, ξi*为松弛变量; ε为不敏感损失函数; C为惩罚参数; αi,αi*,βi,βi*为拉格朗日算子,并且式(5)对参数ω,b,ξi,ξi*的偏导都为0; xi为输入值; yi为观测值。
将式(5)转化为矩阵形式
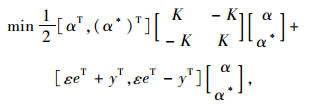
|
(6) |
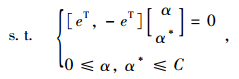
|
(7) |
式中, α=[α1, …,αi, …,αm]和α*=[α1*, …,αi*, …,αm*](i=1, 2,…, m)为拉格朗日算子; m为支持向量个数; e=[1, …,1]T; K(x, xi)为核函数,它接受低维空间的输入值xi,能算出高维空间的内积值。
求解得到回归函数为:
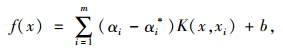
|
(8) |
式中m为支持向量个数。
核函数选取径向基核函数,其表达式为:
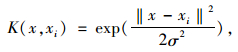
|
(9) |
式中σ为核函数参数。
2 GA-SVR预测建模SVR预测精度与惩罚参数C、核函数参数σ、不敏感损失函数ε有关。核函数参数σ的改变即改变映射函数参数和函数关系,进而改变样本映射特征空间的复杂程度,所以SVR性能的优劣较大程度上也受到σ的影响[19]。同时,C和ε是实现错分样本比例和算法复杂程度之间的折衷,在确定的特征子空间中调节学习机器置信范围和经验风险的比例,对SVR的泛化推广能力也有较大的影响[17, 20]。基于上述分析,本文尝试实现同时对上述3个参数进行组合和优化,以提高参数选择的精度和效率。鉴于GA在参数寻优方面的优势,本文将采用GA对SVR的上述3种参数进行优化,实现短期交通流预测。其预测流程如图 1所示。
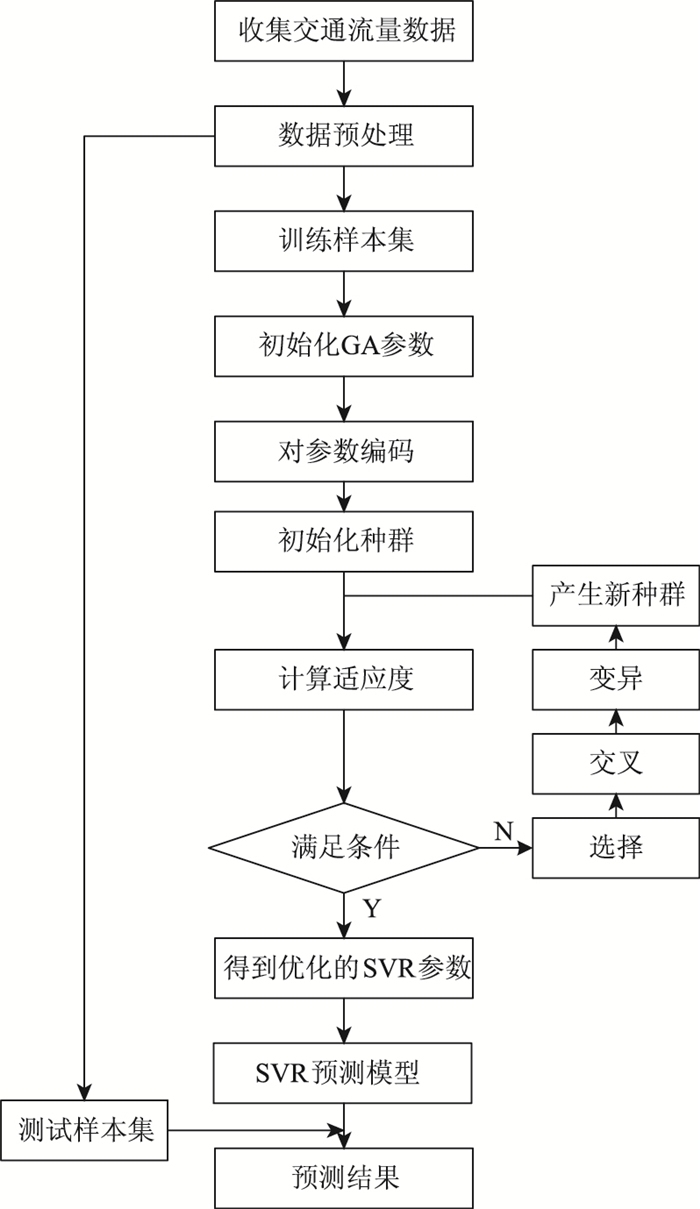
|
| 图 1 GA-SVR预测建模流程图 Fig. 1 Flowchart of prediction modeling based on GA-SVR |
| |
(1) 获取交通流量数据,并且对其进行预处理,得到训练样本集和测试样本集。
(2) 初始化GA参数及对SVR参数进行编码。本文采用实数编码方式,该编码方式避免了二进制编码中的解码和编码过程,并且克服了二进制编码长度有限问题,提高了遗传算法的性能及精度。
(3) 初始化种群并计算适应度。适应度计算采用K-交叉验证(K-fold Cross Validation, K-CV)后的均方误差平均值作为适应度值,衡量选取参数的优劣。
(4) 判断是否满足迭代条件。如果不满足则进行选择、交叉和变异操作,其中选择操作采用轮盘赌方法,选择适应度值高的种群进入下一代;交叉操作采用线性组合的方式,以某概率p(p∈[0, 1])对两个染色体进行交叉操作,即:
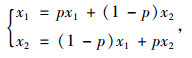
|
(10) |
式中x1,x2分别为两条染色体。
变异操作采用均匀变异方式。如果满足条件则输出SVR参数。
(5) 构造SVR预测模型,将GA最终得到的参数代入SVR预测模型中进行仿真预测。
3 实例验证 3.1 数据获取与处理本文使用美国加州PeMS系统402391号检测器采集的数据进行仿真试验,数据检测周期为5 min,采样时间为2014-05-01 0:00至2014-07-02 24:00,数据共9星期18 144组。
由于检测器在数据采集和传输过程中易受到噪声干扰,需要对所获取的数据进行降噪处理,本文采用算数平均滤波法,即以该信号为中心,将前后连续k个信号进行算术平均值作为该信号值,如式(9)所示。
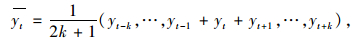
|
(9) |
式中,ȳt为去噪后实际值,yt为t时刻记录值,yt±k为前后k时刻记录值,本文k取值为2。
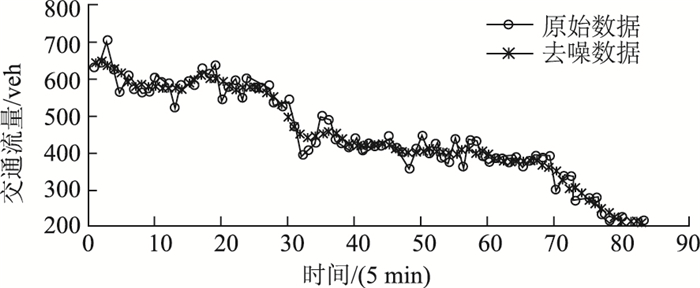
以2014-05-01全天交通数据为例,降噪处理结果如图 2所示。可以看出,原始数据曲线由于噪声存在,含有大量波峰波谷,经过降噪处理后,数据曲线比较光滑而且规律性较此前更明显。
|
| 图 2 数据降噪前后对比 Fig. 2 Comparison data before and after denoising |
| |
3.2 预测结果
为了验证不同形式的时间序列数据对本文模型参数选择及预测的影响,采用3种类型的时间序列数据进行试验并对相同时间序列进行验证,本文选取2014-06-27(星期五) 17:05-23:55共83个采样点进行预测和验证。选择相同维数的训练样本保证3种组合在该模型中具有相同的学习能力,取输入矢量维数为5,构建训练样本集。
(1) 构建星期五时间序列预测集。即利用2014-05-16,2014-05-23,2014-05-30,2014-06-06,2014-06-13,2014-06-20相邻6个星期五时间进行模型参数训练,对2014-06-27进行预测。用2014-05-16,2014-05-23,2014-05-30,2014-06-06,2014-06-13共5个星期五17:05-23:55的83个采样点作为训练样本集输入矢量,2014-06-20相对应的采样点作为训练样本集输出矢量,训练得到模型参数。随后用2014-05-23,2014-05-30,2014-06-06,2014-06-13,2014-06-20共5天的83个采样点作为预测集的输入矢量,2014-06-27这天17:05-23:55的83个采样点作为预测集的输出矢量,如式(10)~(11)所示。预测结果如图 3所示。
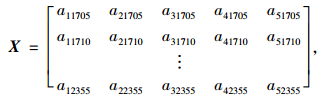
|
(10) |
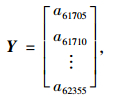
|
(11) |
式中,a11705表示第1天17:00采样点交通数据;a52355表示第5天23:55交通数据;X为输入矢量;Y为输出矢量。
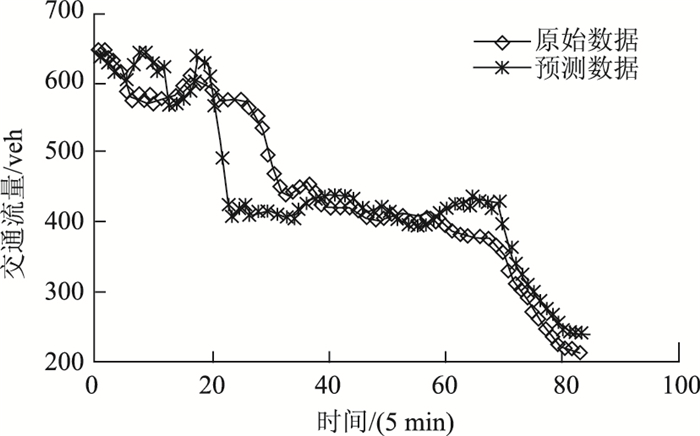
|
| 图 3 周五时间序列预测结果 Fig. 3 Result of Friday time series forecasting |
| |
(2) 构建相邻前5个工作日时间序列预测集。即利用2014-06-19, 2014-06-20, 2014-06-23, 2014-06-24, 2014-06-25, 2014-06-26相邻前6个工作日的交通流量数据进行模型参数训练。用2014-06-19, 2014-06-20, 2014-06-23, 2014-06-24, 2014-06-25共5天17:05-23:55的83个采样点作为训练样本集输入矢量,2014-06-26对应的采样点作为训练样本输出矢量训练得到本模型参数。随后用2014-06-20,2014-06-23,2014-06-24,2014-06-25,2014-06-26共5天的83个采样点作为预测集的输入矢量,用2014-06-27这天17:05-23:55的83个采样点为预测集的输出矢量,如式(10)~(11)所示。预测结果如图 4所示。
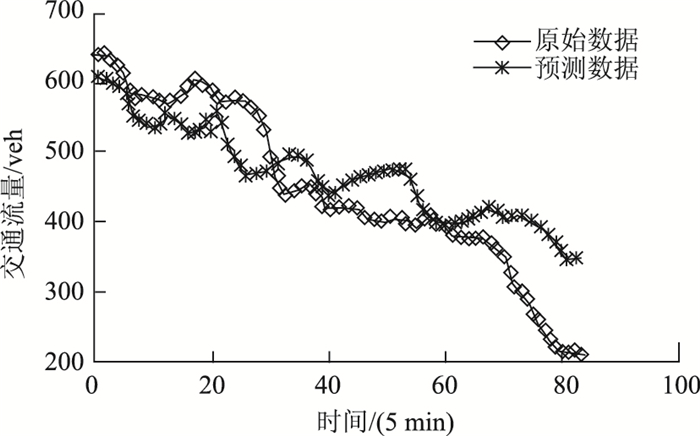
|
| 图 4 五个工作日时间序列预测结果 Fig. 4 Result of forecasting 5 working days time series |
| |
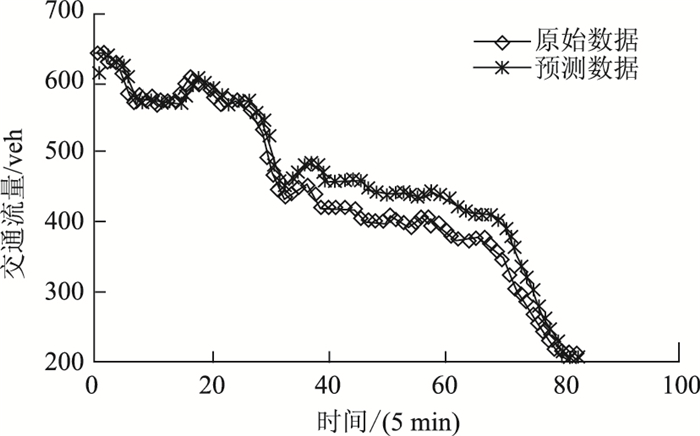
(3) 构建当天的时间序列预测集, 即利用2014-06-27当天的交通流量数据进行预测。前5个采样点为输入矢量,第6个采样点为输出矢量,以此类推,其数据形式如下:用2014-06-27的时间段0:00-16:35, 0:05-16:40, 0:10-16:45, 0:15-16:50, 0:20-16:55的采样点作为训练样本集输入矢量; 16:40-23:30, 16:45-23:35, 16:50-23:40, 16:55-23:45, 17:00-23:50的采样点作为预测集的输入矢量; 17:05-23:55的采样点作为预测的输出矢量,如式(12)~(13)所示。
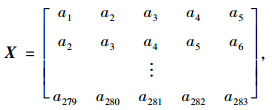
|
(12) |
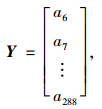
|
(13) |
式中, a1~a288为1~288采样点的交通流量数据;X为输入矢量; Y为输出矢量。
|
| 图 5 当天时间序列预测结果 Fig. 5 Result of forecasting on the day time series |
| |
3.3 分析
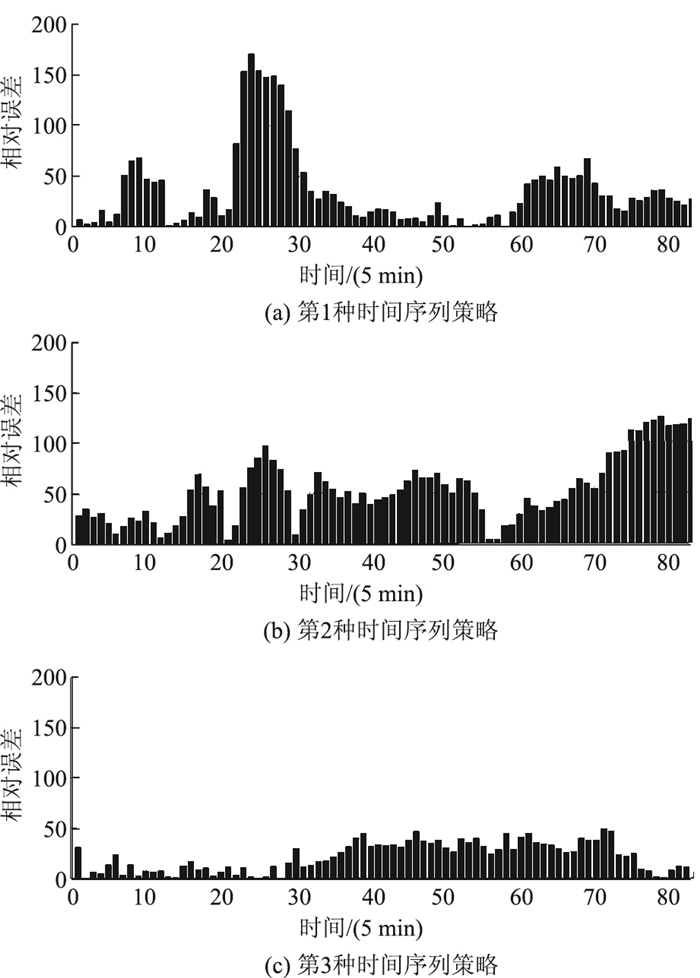
模型不同时间序列预测结果相对误差如图 6所示,其中第1种策略相对误差在采样点20~30时间段内误差较大,而在40~60之间较小,造成相对误差较大的原因主要是训练样本集在20~30时间段内交通流量不稳定;第2种策略总体相对误差都较大,原因主要为每天交通流量存在一定差异,训练得到的参数不适合后一天交通流量的预测;第3种策略在0~30时间段内相对误差较小,预测精度较高,在35~70时间段内相对误差较大,其中在40~60之间相对误差大于第1种模型,但总体预测精度优于其他两种,原因在于当天半小时内交通流量变化较小,能够较好地训练而得到预测参数。
|
| 图 6 不同策略交通流量相对误差 Fig. 6 Relative errors of traffic volume by different strategies |
| |
为了定量分析本文模型的预测效果,引入两个评价指标:平均相对误差(MAE)和平均相对误差百分比(MAPE),并将文中的方法与传统的SVR的预测误差进行比较。MAE和MAPE的定义如下:
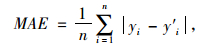
|
(12) |
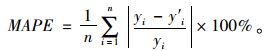
|
(13) |
两种模型3种不同数据组合形式的预测误差比较见表 1。
| 模型 | 预测策略 | MAE | MAPE/% |
| GA-SVR | 1 | 36.902 8 | 11.47 |
| 2 | 53.361 6 | 14.83 | |
| 3 | 25.443 5 | 6.48 | |
| SVR | 1 | 38.301 0 | 9.15 |
| 2 | 59.240 3 | 16.66 | |
| 3 | 36.142 3 | 8.38 |
表 1表明,GA-SVR预测模型的MAE和MAPE均优于SVR预测模型,并且对于同一种预测模型不同类型的时间序列中,第3种时间序列的预测精度明显高于其他两种。
4 结论针对短期交通流量非线性、规律性弱的特点,本文提出了遗传算法和支持向量回归的预测模型,并且针对不同时间序列制订了3种预测策略的交通流量数据形式进行预测,结果表明利用当天的数据进行预测具有更好的预测精度。通过与传统SVR预测模型相比,GA-SVR模型能够较好地得出SVR参数并且准确预测交通流量,为短期交通流量预测提供了一种新的解决方法。
| [1] | 李德仁, 李清泉, 杨必胜, 等. 3S技术与智能交通[J]. 武汉大学学报:信息科学版 , 2008, 33 (4) : 331-336 LI De-ren, LI Qing-quan, YANG Bi-sheng, et al. Techniques of GIS, GPS and RS for the Development of Intelligent Transportation[J]. Geomatics and Information Science of Wuhan University , 2008, 33 (4) : 331-336 |
| [2] | 袁健, 范炳全. 城市道路短期交通流预测VHSSA模型[J]. 公路交通科技 , 2014, 31 (5) : 135-146 YUAN Jian, FAN Bing-quan. VHSSA Model for Predicting Short-term Traffic Flow of Urban Road[J]. Journal of Highway and Transportation Research and Development , 2014, 31 (5) : 135-146 |
| [3] | 张晓利, 陆化普. 非参数回归方法在短时交通流预测中的应用[J]. 清华大学学报:自然科学版 , 2009, 49 (9) : 1471-1475 ZHANG Xiao-li, LU Hua-pu. Non-parametric Regression and Application for Short-term Traffic Flow Forecasting[J]. Journal of Tsinghua University:Science and Technology Edition , 2009, 49 (9) : 1471-1475 |
| [4] | YADAV R K, BALAKRISHNAN M. Comparative Evaluation of ARIMA and ANFIS for Modeling of Wireless Network Traffic Time Series[J]. Eurasip Journal on Wireless Communications & Networking , 2014, 2014 (1) : 1-8 |
| [5] | ANTONIOU C, KOUTSOPOULOS H N, YANNIS G. An efficient Non-linear Kalman Filtering Algorithm Using Simultaneous Perturbation and Applications in Traffic Estimation and Prediction[C]//Intelligent Transportation Systems Conference, 2007. Seattle, WA:IEEE, 2007:291-299. |
| [6] | 聂佩林, 余志, 何兆成. 基于约束卡尔曼滤波的短时交通流量组合预测模型[J]. 交通运输工程学报 , 2008, 8 (5) : 86-90 NIE Pei-lin, YU Zhi, HE Zhao-cheng. Constrained Kalman Filter Combined Predictor for Short-term Traffic Flow[J]. Journal of Traffic and Transportation Engineering , 2008, 8 (5) : 86-90 |
| [7] | 董春娇, 邵春福, 周雪梅, 等. 基于交通流参数相关的阻塞流短时预测卡尔曼滤波算法[J]. 东南大学学报:自然科学版 , 2014, 44 (2) : 413-419 DONG Chun-jiao, SHAO Chun-fu, ZHOU Xue-mei, et al. Kalman Filter Algorithm for Short-term Jam Traffic Prediction Based on Traffic Parameter Correlation[J]. Journal of Southeast University:Natural Science Edition , 2014, 44 (2) : 413-419 |
| [8] | 齐驰, 侯忠生. 自适应单指数平滑法在短期交通流预测中的应用[J]. 控制理论与应用 , 2012, 29 (4) : 465-469 QI Chi, HOU Zhong-sheng. Application of Adaptive Single-exponent Smoothing for Short-term Traffic Flow Prediction[J]. Control Theory & Applications , 2012, 29 (4) : 465-469 |
| [9] | 陈杨, 刘光勇, 唐海周, 等. 一种基于平衡指数平滑的交通流数据预测方法[J]. 现代计算机 , 2014 (7) : 45-48 CHEN Yang, LIU Guang-yong, TANG Hai-zhou, et al. The Prediction Method for Traffic Flow Data Based on the Balance of Exponential Smoothing[J]. Modern Computer , 2014 (7) : 45-48 |
| [10] | 邬月春.基于动态模糊神经网络的交通流预测[D].兰州:兰州交通大学, 2013. WU Yue-chun. Research on Prediction of Traffic Flow Based on Dynamic-fuzzy Neural Network[D]. Lanzhou:Lanzhou Jiaotong University, 2013. |
| [11] | 王军, 许宏科, 蔡晓峰, 等. 基于BP神经网络的高速公路动态交通流预测[J]. 公路交通技术 , 2007 (1) : 150-152 WANG Jun, XU Hong-ke, CAI Xiao-feng, et al. Expressway Dynamic Traffic Flow Prediction Based on BP Neural Network[J]. Technology of Highway and Transport , 2007 (1) : 150-152 |
| [12] | 王凡.基于支持向量机的交通流预测方法研究[D].大连:大连理工大学, 2010. WANG Fan. Research on Method of Traffic Flow Forecasting Based on SVM[D].Dalian:Dalian University of Technology, 2010. |
| [13] | 傅贵, 韩国强, 逯峰, 等. 基于支持向量机回归的短时交通流预测模型[J]. 华南理工大学学报:自然科学版 , 2013, 41 (9) : 71-76 FU Gui, HAN Guo-qiang, LU Feng, et al. Short-term Traffic Flow Forecasting Model Based on Support Vector Machine Regression[J]. Journal of South China University of Technology:Natural Science Edition , 2013, 41 (9) : 71-76 |
| [14] | SMITH B L, WILLIAMS R M, OSWALD R K. Comparison of Parametric and Nonparametric Models for Traffic Flow Forecasting[J]. Transportation Research Part C:Emerging Technologies , 2002, 10 (4) : 303-321 |
| [15] | 翁剑成, 荣建, 任福田, 等.基于非参数回归的快速路行程速度短期预测算法[J].公路交通科技, 2007, 24(3):93-97, 106. WENG Jian-cheng, RONG Jian, REN Fu-tian, et al. Non-parametric Regression Model Based Short-term Prediction for Expressway Travel Speed, 2007, 24(3):93-97, 106. http://manu12.magtech.com.cn/Jweb_gljtkj/CN/abstract/abstract11020.shtml |
| [16] | 于滨, 邬珊华, 王明华, 等. K近邻短时交通流预测模型[J]. 交通运输工程学报 , 2012, 12 (2) : 105-111 YU Bin, WU Shan-hua, WANG Ming-hua, et al. K-nearest Neighbor Model of Short-term Traffic Flow Forecast[J]. Journal of Traffic and Transportation Engineering , 2012, 12 (2) : 105-111 |
| [17] | 刘爱国, 薛云涛, 胡江鹭, 等. 基于GA优化SVM的风电功率的超短期预测[J]. 电力系统保护与控制 , 2015, 43 (2) : 90-95 LIU Ai-guo, XUE Yun-tao, HU Jiang-lu, et al. Ultra-short-term Wind Power Forecasting Based on SVM Optimized by GA[J]. Power System Protection and Control , 2015, 43 (2) : 90-95 |
| [18] | 朱国强, 刘士荣, 俞金寿. 支持向量机及其在函数逼近中的应用[J]. 华东理工大学学报 , 2002, 28 (5) : 555-559, 568 ZHU Guo-qiang, LIU Shi-rong, YU Jin-shou. Support Vector Machine and Its Applications to Function Approximation[J]. Journal of East China University of Science and Technology , 2002, 28 (5) : 555-559, 568 |
| [19] | FUKUSHI D, SHICHIRI M, SUGIYAMA S, Et al. Scanning Near-field Optical/Atomic Force Microscopy Detection of Fluorescence in-situ Hybridization Signals Beyond the Optical Limit[J]. Experimental Cell Research , 2003, 289 (2) : 237-244 |
| [20] | SAINI L M, AGGARWAL S K, KUMAR A. Parameter Optimization Using Genetic Algorithm for Support Vector Machine-based Price-forecasting Model in National Electricity Market[J]. IET Generation, Transmission & Distribution , 2010, 4 (1) : 310-315 |
 2017, Vol. 34
2017, Vol. 34
