扩展功能
文章信息
- 杨刚, 张东好, 李克强, 罗禹贡
- YANG Gang, ZHANG Dong-hao, LI Ke-qiang, LUO Yu-gong
- 基于车车通信的车辆并行协同自动换道控制
- Cooperative Same-direction Automated Lane-changing Based on Vehicle-to-vehicle Communication
- 公路交通科技, 2017, 34(1): 120-129, 136
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 120-129, 136
- 10.3969/j.issn.1002-0268.2017.01.017
-
文章历史
- 收稿日期: 2016-03-13
2. 北京电动车辆协同创新中心, 北京 100081
2. Beijing Collaborative Innovation Center of Electric Vehicles, Beijing 100081, China
车辆跟驰行为和换道行为是两个最基本的驾驶行为,其中驾驶员换道行为相比于跟驰行为,考虑的车辆更多,决策过程复杂,难以描述[1]。据相关调查表明,换道导致的交通事故所占的比例约5%,交通延迟约占10%[2];75%的换道事故是因为驾驶员在换道事故中对周围的环境感知不足导致的[3]。而自动换道是智能驾驶中的研究热点,其主要通过轨迹规划和轨迹跟踪实现换道[4]。此外,随着通信技术的发展,换道车辆能够实时获得周围相关车辆的运动状态信息,增强了自车对周围环境的判断能力,为多车协同提供了通信基础。因此基于车车通信协同自动换道控制策略研究十分重要[5]。
Y Luo等人针对目前自动换道未考虑周围相关车辆的状态变化的问题,提出了基于车车通信的动态自动换道控制策略[6]。自动换道车辆在换道过程中能够实时根据换道车辆的状态重新规划轨迹,保证换道车辆的安全性。但周围相关车辆状态改变主要指纵向上的加减速,未考虑其他相关车辆的横向运动(如换道)。
Matthias等人通过调研试验分析驾驶员换道过程中目标车道后车在换道车辆不同换道操作时做出的反应[7-8]。试验结果表明,驾驶员的协同换道行为能够提高换道车辆的安全性,而且目标车道后车更易通过换道来协同原换道车辆。
李珣等人为研究交通流模型中的局部交通规则,提出了考虑局部区域车辆状态的优化的协同换道模型,并制订了共线协同换道和并行协同换道规则[9],分析了两车协同换道对交通流的影响。结果表明,协同换道能够提高交通效率,但协同规则简单,有待进一步研究。
协同换道能够提高车辆的安全性和换道效率,其研究具有重要意义。但目前协同换道尚未形成一个统一定义,多指换道车辆在换道过程中,目标车道后车通过减速或换道为原换道车辆提供足够的换道安全距离[10]。相关研究基于驾驶员试验分析换道过程中的协同行为,提出了驾驶协同换道辅助系统[11]。在合流区研究中,车辆汇流也会涉及到车辆之间的协同行为[12]。另外随着通信技术、计算机技术的发展,多车道自动驾驶将成为可能。而目前还鲜有对自动驾驶环境下的三车道的协同行为开展研究,特别是在三车道中,两车同时变换车道而产生的协同行为。因此本文分析了三车道场景下的协同行为,建立了两车并行协同模型,提出了基于车车通信的两车并行自动换道的协同控制策略。
本研究基于三车道八车场景,其所有车辆可控,并有两车换道,六车直行。场景中所有车辆通过自车传感器获得车辆的状态信息(如GPS、加速度传感器、横摆角传感器等获得位置、速度、加速度和横摆角等),并通过车车通信将车辆的状态信息和驾驶意图传送到场景中的其他车辆(或者协同控制单元)。本文认为其通信理想,无延迟丢包。
本文以两车并行自动换道为研究重点,通过传统安全距离模型检测与场景非换道车辆的安全距离,再通过本文提出的协同换道安全距离模型检测两辆换道车辆之间的安全距离,制定安全的协同换道轨迹。按照规划的轨迹进行跟踪,进行安全、舒适地换道。最后通过Matlab/Simulink联合Carsim仿真验证并行协同自动换道控制策略的有效性。
1 并行协同自动换道分析和控制架构 1.1 并行协同自动换道情景界定三车道八辆车的场景中,两辆换道车辆同时从同一车道换向高速车道,如图 1(a)至(f)所示;或者两辆换道车辆中,一辆换道车辆先从原车道换道高速(或低速车道),另一辆车辆同时换向第一辆换道车辆的车道,如图 1(g)和(h)所示。场景图 1(a)至(f)中,车辆换道方向一致,只是换道初速度不一致,如图 1(a)和(b)所示;或者换道目标速度为减速,如图 1(c)和(d)所示;或者换道的初始(或目标车道)车辆中间存在车辆,如图 1(e)和(f)所示。这些场景只是初始的速度或者目标速度不一样,因此都可以归结为图 1(a)的场景;而图 1(g)和(h)的场景为初始时刻不同车道的特殊场景,可以归为另一类,所以图 1(a)和(e)为协同换道的典型场景。

|
| 图 1 并行协同换道场景 Fig. 1 Scenario of cooperative same-direction lane-changing |
| |
观察图 1中换道车辆的起始位置和终点位置,根据两辆换道车辆的方向,如图 2中的虚线所示,将其定义为并行协同换道。并行协同换道包括两辆换道车辆,而且其换道方向一致。

|
| 图 2 并行协同换道场景分类(虚线箭头为换道方向示意) Fig. 2 Classification of scenario of cooperative same-direction lane-changing |
| |
1.2 协同自动换道控制架构
本文提出的并行协同自动换道控制架构如图 3所示。

|
| 图 3 并行协同自动换道控制架构 Fig. 3 Structure of cooperative automated same direction lane-changing |
| |
并行协同控制单元通过车车通信,获得上述场景中各车辆的位置、速度、加速度和横摆角等状态量。控制单元把收集到的信息分为换道车辆和非换道车辆两类,并对换道车辆进行轨迹规划,对非换道车辆进行匀速运动轨迹规划。其中,根据单车安全距离模型建立换道车辆与周围环境中的非换道车辆的安全距离模型;根据并行协同安全距离模型建立换道车辆之间的安全距离模型,并添加到车辆轨迹规划的约束中;并行协同单元把规划的轨迹通过车车通信传送给场景中的各个车辆; 最后各个车辆的换道轨迹跟踪器根据最优规划轨迹和自车实际行驶状态信息,通过模型预测控制跟踪控制算法,计算出每辆换道车辆和非换道车辆的控制量,如前轮转角、驱动转矩等,使两辆换道车辆能够安全高效地换道。
2 并行协同自动换道控制器的设计 2.1 轨迹规划(1) 安全距离模型
车辆在换道过程中,不仅要考虑自身的最优轨迹,而且应该考虑与周围车辆的安全性。并行协同自动换道过程中首要考虑的是协同车辆之间的安全距离模型;其次还需要考虑与周围非换道车辆的安全距离模型。
换道车辆与换道车辆之间的安全距离模型。对于并行换道车辆之间的安全距离检测,本文针对并行换道提出了并行协同自动换道安全距离模型,分析如下:
以典型换道场景为例,如图 4所示,其中M1车的后保险杠的实心点表示换道车辆M1和M2的临界碰撞点,两辆换道车辆相邻,同时从低速车道换向中速车道。车辆在碰撞过程中肯定存在一个临界碰撞点,只要车辆换道前的距离大于临界安全距离,那么车辆换道就是安全的,即是说临界碰撞的最大值就是安全距离的最小值,所以分析临界碰撞是并行协同安全距离模型的关键。在两辆车换道过程中(不考虑换道超车),临界碰撞形式有2类,4种:一是,当两车横摆角θ1 < θ2时,M2的前保险杠与M1的棱角点碰撞,或者M2的棱角点与M1的后保险杠碰撞;二是,当θ1>θ2时,M2的左前方棱角点与M1的后保险杠碰撞,或者M2的前保险杠与M1的后保险杠碰撞,如图 5所示。

|
| 图 4 并行协同自动换道安全距离模型场景 Fig. 4 Safety spacing model scenario of same direction lane-changing safety spacing scenario between lane-changeing vehicles |
| |

|
| 图 5 并行协同自动换道车辆临界碰撞形式 Fig. 5 Critical collisions of cooperative automated same direction lane-changing |
| |
对于临界碰撞形式1,结合换道车辆的位置和车辆的几何形状大小,临界碰撞方程在横向上可以列出式(1),纵向上可以列出式(2)。

|
(1) |

|
(2) |
式中,dclls1为临界碰撞时的距离; x1, x2, y1, y2, θ1, θ2为换道车辆的纵横向位置和横摆角; Lr1为车辆M1几何中心到后保险杠的距离;Lf2为车辆M2几何中心到前保险杠的距离;L为车长,B1为车辆M1车宽; b2为车辆M2碰撞点到车辆保险杠中点的二倍; tc为碰撞时刻; 下标1,2代表换道车辆M1,M2。
临界碰撞时,因为碰撞点为点与线的碰撞,不能像单车换道安全距离模型一样直接求出临界碰撞时刻tc,其次碰撞过程中碰撞点到保险杠中点距离,如图 5所示,A点到M1后保险杠的距离b,也是不能直接求出的。所以式(1)、(2)两个方程含有3个变量dlls1, tc, b,是一个静不定方程,并不能解出安全距离dlls1确切值。而安全距离是保证车辆换道的最小距离,同时也是车辆临界碰撞的最大距离,于是把式(1)、(2)转化为求解临界碰撞的最大值,并添加几何约束和时间约束,结果如式(3)所示。另外在换道过程中,为保证车辆之间的安全,车辆的最小安全距离必须考虑换道过程中的跟踪误差和突发事件安全性,所以式中加入了动态安全车距项[13],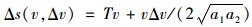

|

|
(3) |
式中,tf1, tf2为换道车辆完成换道时间; B2为车辆M2的车宽; Th为车头时距; Δv为车辆M1相对M2车速; V2为车辆M2的速度;a1, a2为M1, M2的最大加速度和减速度。
同理可以推导出临界碰撞形式2, 3和4的数学模型(第3, 4种类似,这里不再列出),其第2种如式(4)所示。

|
(4) |

|
式中, b1为车辆M1碰撞点到车辆保险杠中点的二倍。
综合临界碰撞的结果,最小安全距离模型为:

|
(5) |
式中,MSS (M1, M2)代表M1和M2之间的最小安全距离。
观察式(3)、(4),可以看出这是一个含有tc, b变量,带有边界条件的非线性优化问题。针对这类问题,可以通过内点法求出数值解,得到最大临界碰撞距离,也就是最小安全距离,保证换道车辆之间的安全性。
换道车辆与直行车辆之间的安全距离模型。针对换道车辆与非换道车辆的安全距离模型,本研究采用Jula等人[14]提出的安全距离模型。该模型的场景如图 6所示,其具体模型见式(9)。场景中,只有一辆换道车辆,其他车辆保持已知的运动状态(初始速度,加速度已知),通过保证换道过程中的最小安全距离的安全,从而保证整个换道过程的安全性。

|
| 图 6 单车换道安全距离模型场景 Fig. 6 Safety spacing model scenarios of single lane-changing |
| |

|
(6) |
式中,v, a分别为速度和加速度,下标M, Ld, Fd, Lo, Fd分别代表换道车辆、目标车道前车、目标车道后车、原车道前车、原车道后车; tc, tf为临界碰撞时刻和换道结束时刻;τ, λ为积分变量。
(2) 轨迹制定
目前轨迹规划的研究主要有基于梯形横向加速度的换道轨迹规划方法、基于样条曲线的换道轨迹规划方法、基于回旋曲线的换道轨迹规划方法、基于多项式函数的换道轨迹规划方法、基于人工势场的换道轨迹规划方法等[15]。其中基于多项式函数的换道轨迹具有3次连续可导,曲率连续不突变的特点,如式(7)所示。

|
(7) |
式中,ai, bi(i=0, 1, …, 5)为多项式系数;x, y为纵、横向坐标;t为换道时刻。
式中有12个未知数,根据换道轨迹的初始和结束时的纵横向位置、速度、加速度,可以建立12个方程,但同时引入了2个未知数,换道结束时刻和横向位移。所以这是一个静不定方程组,欲求解,可转化为最优性能指标的形式,如式(8)所示。最优性能指标以纵横向的加加速度(加速度变化率)积分为目标,反映轨迹的舒适性;以换道纵向距离为目标,反映换道过程合理性和安全性。两条轨迹指标之间进行无量纲化,并通过权重系数相加实现多个性能指标的融合,其值采用采用经验估计法得到。

|
(8) |
式中,w11, w12, w13, w21, w22, w23为权重系数;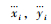
在式(8)中还要满足换道过程中的几何约束、车辆自身的动力学约束和安全距离约束,如

|
(9) |
式中,wi为目标车道与原车道的几何中线间距;dxinMi, j为换道车辆Mi与车辆i的初始纵向距离。
通过以上方程把轨迹规划问题转化为了一个以换道结束时间,横向位置为变量的最优问题。从式(7)~(9)可以看出,该最优问题是一个带约束的非线性问题,无法直接解析求解。因此采用外点法数值求解,得到换道最优轨迹时间序列,保证换道过程中的舒适性[16]。
2.2 模型预测轨迹跟踪控制本研究场景中的车辆处于线性范围内,所以为了减小计算复杂度,选取三自由度的运动学模型[17],如式(10)所示。

|
(10) |
式中,x为车辆横向坐标; y为车辆纵向坐标; φ为车辆横摆角; ω为车辆横摆角速度。
假设转向过程中,车辆质心侧偏角保持不变,即车辆的瞬时转向半径与轨迹曲率半径相同,则有ω=vtan δf/l,代入式(10)。对于理想参考轨迹,每一个点都满足上述方程,则在参考轨迹点ẋr=xr, yr, φr, u=vr, δfr泰勒展开,并舍去高阶项,并令误差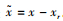

|
(11) |
式中,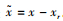
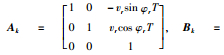
以式(11)为误差状态方程进行模型预测控制器设计。在轨迹跟踪过程中,要求保证车辆的实际轨迹与参考轨迹误差及控制量的变化量也尽可能小,所以选取纵横向位移,横摆角的二次项作为误差控制项,速度和前轮转角的增量作为控制变化约束项,具体表达式如式(12)所示。

|
(12) |
式中,k为当前时刻; np为预测时域; nc为控制时域; Δu为控制增量; Q, R为权重矩阵。
以式(12)为目标函数,式(11)为误差状态方程进行模型预测控制器设计。推导过程中,假设预测时域内系统线性时不变,即Ak, Bk为常数,加入松弛因子以防止没有可行解的情况。最后舍去常数项,转化为标准的二次型,得到

|
(13) |
式中,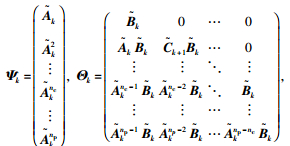
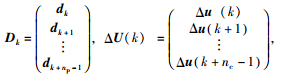
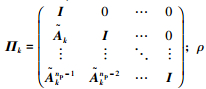
约束条件的设计中[18],无法通过二次型直接对控制量进行约束,但可以将控制变量的约束转化为控制变量增量的约束,转换结果如下:

|
(14) |
式中,Uk为预测时域内的控制输入; ΔUk为控制量增量; Umin, Umax为控制量上下边界; ΔUmin, ΔUmax为控制量增量上下边界约束; Uk-1=lnc⊗u(k-1),
从以上可以看出,模型预测控制就转化为了带约束的二次型控制问题,如式(15)所示。针对该模型,目前的带约束的二次型算法成熟,很快就可以求出最优解。求出解后,为了增加控制有效性,通常将第一个控制分量作为当前时刻的控制输入。最后通过车辆行驶力平衡方程将速度控制转化为车辆的驱动力矩控制。

|
(15) |
为验证整个控制策略的正确性和有效性,建立了基于Simulink和Carsim的联合仿真平台,主要对换道车辆M1和M2进行仿真,见图 7所示。首先设置仿真车辆M1和M2的初始纵向距离,通过s函数建立轨迹规划数学模型生成参考轨迹,并输出控制命令决定车辆是否协同换道;如距离太小不能安全换道,取消协同换道,见图 7(a)。当车辆换道M1或M2得到跟踪命令时,根据车辆状态利用模型预测控制实现轨迹跟踪,见图 7(b)。

|
| 图 7 Simulink和Carsim的联合仿真模型 Fig. 7 Combined simulation model of Simulink with Carsim |
| |
3.2 仿真工况设计
本文针对几种代表性场景进行了仿真分析,各种场景下的主要参数和统计结果如表 1所示。当换道时刻不同时,因为前方车辆先换道更符合日常驾驶场景,所以不失一般性假设前方车辆M1(或M1)先于M2(或M1)换道1 s (M1bfM2表示M1先换道1 s,M2bfM1表示M2先换道1 s)。
| 编号 | 车辆M1 | 车辆M2 | 安全距离 | |||||||
| 原速度-目标速度/ (km·h-1) | 原车道-目标车道 | 换道时间/s | 原速度-目标速度/ (km·h-1) | 原车道-目标车道 | 换道时间/s | 同时换道/m | 不同时换道/m | |||
| 1 | 80~100 | 低速-中速 | 6.09 | 80~100 | 低速-中速 | 6.09 | 41.67 | 36.16 (M1bfM2) | ||
| 2 | 120~100 | 高速-中速 | 6.11 | 120~100 | 高速-中速 | 6.11 | 50 | 46.95 (M1bfM2) | ||
| 3 | 100~120 | 中速-高速 | 6.13 | 80~100 | 低速-中速 | 6.09 | 37.3 | 23.26 (M2bfM1) | ||
| 4 | 120~100 | 高速-中速 | 6.11 | 100~80 | 中速-低速 | 6.09 | 55.6 | 25.98 (M2bfM1) | ||
| 5 | 100~120 | 中速-高速 | 6.13 | 100~120 | 中速-高速 | 6.13 | 50 | 46.95(M1bfM2) | ||
| 6 | 100~80 | 高速-中速 | 6.09 | 100~80 | 高速-中速 | 6.09 | 41.67 | 36.16 (M1bfM2) | ||
上述6种仿真结果中,1到4中场景仿真参数同属于两种场景:同一车道的两车换道至更高速的车道,见图 1(a); 不同车道的两车换向更高或更低车速的车道,如图 1(e)所示。这两种场景代表了并行协同自动换道的主要类型。而1~4组仿真代表不同的初末状态,所以下面就1~4组结果进行详细分析。
3.3 仿真结果分析(1) 同一车道的两车换道至更高速的车道
并行协同自动换道的典型场景就是在同一车道的两车同时换道至高速车道或低速车道,如图 1中(a)~(f)所示,其代表了车辆从中速换向高速车道,从高速换向低速车道等多种场景。针对图 1(a)场景,假设两辆换道车辆的原车道车速均为80 km/h,目标车道车速为100 km/h,根据轨迹规划方程和安全距离模型得到换道车辆的最优换道轨迹,其反映了加速过程中的协同换道控制过程。
本场景下,计算后的最小安全车距为41.67 m,也就是说车辆在理想轨迹形式时,只要换道车辆的换道起始时刻距离大于41.67 m,车辆就可以安全地换道,而且能够容纳跟踪误差或者应对突发情况;当M2后换道1 s时,M1的速度大于同时换道时的速度,因此其安全距离减小到36.16 m。图 8显示了换道纵向初始距离为最小安全距离时,两车换道过程,显然两车无论同时或不同时,车辆都能进行安全地换道。

|
| 图 8 并行协同场景1换道过程 Fig. 8 Lane-changing process of 1st cooperative same direction scenario |
| |
另外,如果单车分别换道,总时间为6.09×2=12.18 s,而并行协同同时换道用时6.09 s,M1先换道1 s时用时7.05 s,均大大提高了换道效率。
类似地,另一场景假设,见图 1(c),反映了减速过程中的并行协同控制。当协同车辆M1, M2处于高速车道时,车辆从高速换道至中速车道,换道车辆的轨迹规划的目标速度为100 km/h,换道前速度为120 km/h。当两车同时换道时,换道车辆之间的安全距离为50 m;当M1先换道1 s时,换道最小安全距离为46.95 m。图 9显示了换道初始纵向距离为最小安全距离时的换道过程,显然车辆都可以安全地完成换道。

|
| 图 9 并行协同场景2换道过程 Fig. 9 Lane-changing process of 2nd cooperative same direction scenario |
| |
(2) 不同车道的两车换向更高或更低车速的车道
在并行协同自动换道的过程中,处于不同车道的换道车辆如果具有换道意图,那么在车车通信的条件下,换道车辆之间互通信息,能够在此复杂的场景下完成高效安全地不同车道之间的并行协同自动换道。换道场景如图 1(g)所示,M1换道前速度为100 km/h,目标车速为120 km/h;M2换道前车速80 km/h,目标换道车速为100 km/h。通过换道车辆之间的安全距离模型检测,两车同时换道时动态安全车距车辆之间的安全车距为37.3 m,当M2先换道时,车辆之间的最小安全距离为23.26 m。当换道初始距离为最小安全距离时,其换道过程如图 10所示,显然换道车辆能安全换道。

|
| 图 10 并行协同场景3换道过程 Fig. 10 Lane-changing process of 3rd cooperative same direction scenario |
| |
换道场景如图 1(h)时,换道车辆M1初始速度为100 km/h,目标车速为80 km/h;换道车辆M2初始速度为120 km/h,目标速度为100 km/h。检测换道车辆之间的安全距离模型,安全车距为55.6 m,当M2先换道1 s时,最小换道安全距离减小为25.98 m,显然M2先换道导致其横向速度增大,预留给M1的换道空间增大,因此最小安全距离减小。当换道初始距离为最小安全距离时,其换道过程如图 11所示,换道车辆显然安全。

|
| 图 11 并行协同场景4换道过程 Fig. 11 Lane-changing process of 4th cooperative same direction scenario |
| |
这些仿真验证了并行协同自动换道控制策略能够保证并行换道过程中的安全,且大大提高了换道效率。
4 结论本文在分析三车道八车换道场景基础上,提出了并行协同自动换道控制策略,并通过仿真系统对所提策略进行了验证,得出以下结论:
(1) 分析了三车道八成场景中可能存在的并行协同场景,界定了并行协同换道类型。
(2) 基于并行协同场景,提出了换道车辆之间的并行协同安全距离模型,解决了换道车辆之间的协同安全问题。
(3) 提出了基于车车通信的两车并行协同自动换道自动控制策略,实现了并行协同场景下的两车安全高效地自动换道控制。
在上述并行协同自动换道研究的基础上,后续研究将着力于驾驶模拟器来验证算法的实时性和有效性,以及进一步界定三车道八车场景下的其他协同类型。
| [1] | 杨小宝. 考虑实施过程的车辆换道模型及其应用[J]. 物理学报 , 2009, 58 (2) : 836-842 YANG Xiao-bao. A Lane-changing Model Considering the Maneuver Process and Its Applications[J]. Acta Physica Sinica , 2009, 58 (2) : 836-842 |
| [2] | AMMOUN S, NASHASHIBI F, LAURGEAU C. An Analysis of the Lane Changing Manoeuvre on Roads:the Contribution of Inter-Vehicle Cooperation via Communication[C]//2007 IEEE Intelligent Vehicles Symposium. Istanbul:IEEE, 2007:1095-1100. |
| [3] | SUN D, ELEFTERIADOU L. Lane-changing Behavior on Urban Streets:A Focus Group-based Study[J]. Applied Ergonomics , 2011, 42 (5) : 682-91 |
| [4] | 李玮, 高德芝, 段建民. 智能车辆自由换道模型研究[J]. 公路交通科技 , 2010, 27 (2) : 119-123 LI Wei, GAO De-zhi, DUAN Jian-min. Research on Lane Change Model for Intelligent Vehicles[J]. Journal of Highway and Transportation Research and Development , 2010, 27 (2) : 119-123 |
| [5] | HU J, KONG L, SHU W, et al. Scheduling of Connected Autonomous Vehicles on Highway Lanes[C]//2012 IEEE Global Communications Conference. Anaheim, CA:IEEE, 2012:5556-5561. |
| [6] | LUO Y, XIANG Y, CAO K, et al. A Dynamic Automated Lane Change Maneuver Based on Vehicle-To-Vehicle Communication[J]. Transportation Research Part C:Emerging Technologies , 2016, 62 : 87-102 |
| [7] | HEESEN M, BAUMANN M, KELSCH J, et al. Investigation of Cooperative Driving Behaviour during Lane Change in a Multi-Driver Simulation Environment[C]//Human Factors:A View from an Integrative Perspective. Toulouse:HFES, 2012:305-318. |
| [8] | KELSCH J, DZIENNUS M, KÖSTER F. Cooperative Lane Change Assistant:Background, Implementation & Evaluation[C]//Proceedings of AAET 2015. Braunschweig:AAET, 2015:65-85. |
| [9] | 李珣, 曲仕茹, 夏余. 车路协同环境下多车道车辆的协同换道规则[J]. 中国公路学报 , 2014, 27 (8) : 97-104 LI Xun, QU Shi-ru, XIA Yu. Cooperative Lane-changing Rules on Multilane under Condition of Cooperative Vehicle and Infrastructure System[J]. China Journal of Highway and Transport , 2014, 27 (8) : 97-104 |
| [10] | MORIARTY D E, LANGLEY P. Learning Cooperative Lane Selection Strategies for Highways[C]//AAAI-98 Proceedings. Cambridge:AAAI Press, 1998:684-691. |
| [11] | KATO S, TSUGAWA S, TOKUDA K, et al. Vehicle Control Algorithms for Cooperative Driving with Automated Vehicles and Intervehicle Communications[J]. IEEE Transactions on Intelligent Transportation Systems , 2002, 3 (3) : 155-161 |
| [12] | DAAMEN W, LOOT M, HOOGENDOORN S. Empirical Analysis of Merging Behavior at Freeway On-ramp[J]. Transportation Research Record , 2010, 2188 : 108-118 |
| [13] | TREIBER M, HENNECKE A, HELBING D. Congested Traffic States in Empirical Observations and Microscopic Simulations[J]. Physical Review E:Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics , 2000, 62 (2 Pt A) : 1805-1824 |
| [14] | JULA H, KOSMATOPOULOS E B, IOANNOU P A. Collision Avoidance Analysis for Lane Changing and Merging[J]. IEEE Transactions on Vehicular Technology , 2000, 49 (6) : 2295-2308 |
| [15] | XU G, LIU L, OU Y, et al. Dynamic Modeling of Driver Control Strategy of Lane-change Behavior and Trajectory Planning for Collision Prediction[J]. IEEE Transactions on Intelligent Transportation Systems , 2012, 13 (3) : 1138-1155 |
| [16] | 向勇, 罗禹贡, 曹坤, 等. 基于车-车通信的自动换道控制[J]. 公路交通科技 , 2016, 33 (3) : 120-126, 145 XIANG Yong, LUO Yu-gong, CAO Kun, et al. Automatic Lane Change Control Based on Vehicle-to-vehicle Communications[J]. Journal of Highway and Transportation Research and Development , 2016, 33 (3) : 120-126, 145 |
| [17] | 姜岩, 龚建伟. 无人驾驶车辆模型预测控制[M]. 北京: 北京理工大学出版社, 2014 . JIANG Yan, GONG Jian-wei. Predictive Control for Self-driving Vehicle Model[M]. Beijing: Beijing Institute of Technology Press, 2014 . |
| [18] | 李升波, 王建强, 李克强. 软约束线性模型预测控制系统的稳定性方法[J]. 清华大学学报:自然科学版 , 2010, 50 (11) : 1848-1852 LI Sheng-bo, WANG Jian-qiang, LI Ke-qiang. Stabilization of Linear Predictive Control System with Softening Constraints[J]. Journal of Tsinghua University:Natural Science Edition , 2010, 50 (11) : 1848-1852 |
 2017, Vol. 34
2017, Vol. 34
