扩展功能
文章信息
- 夏亮, 郭廷龙, 刘仰, 江欣国
- XIA Liang, GUO Ting-long, LIU Yang, JIANG Xin-guo
- 基于多值CA模型的两轮车加速过程建模与分析
- Simulation and Analysis of Two-wheel Vehicle Acceleration Based on Multi-value CA Model
- 公路交通科技, 2017, 34(1): 112-119
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 112-119
- 10.3969/j.issn.1002-0268.2017.01.016
-
文章历史
- 收稿日期: 2016-03-24
2. 综合交通运输智能化国家地方联合工程实验室, 四川 成都 610031
2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu Sichuan 610031, China
交通流理论作为运用数学和物理定律来描述交通特性的一门边缘学科,其研究不仅受到了交通工程学者的重视,而且引起了广大物理学家的兴趣。在研究方法上,交通流模型分为宏观连续模型[1-2]、介观气体动理论模型[3-4]和微观模型[5-8],其中微观模型包括跟驰模型[5-6]和元胞自动机模型[7-8]。元胞自动机(Cellular Automaton, CA)模型因为具有计算速度快、易于计算机操作、灵活度高等特性,常被用于交通流模拟研究。
1992年,Nagel等[9]最早提出了一种简单的一维单车道元胞自动机交通流模型,即NaSch模型,随后出现了恒速控制模型、慢启动模型和基于时间的CA模型等一维单车道拓展模型[10]。虽然一维元胞自动机模型能再现一些实际的交通现象,如自发产生的拥堵现象和拥堵交通情况下的时走时停波,但是其简单的模型结果无法适用于多车道复杂的仿真环境。因此,1998年Nagel等[11]在NaSch模型的基础上提出了考虑车辆换道行为的多车道元胞自动机仿真模型。而后多车道元胞自动机仿真模型作为基础模型被广泛用于机动车流微观仿真研究[7-8]。2000年,Nishinari等[12]将宏观流体动力学模型中的Burger方程经过离散化处理得到最大速度为1个元胞/仿真步(此后未特别说明时,速度单位为个元胞/仿真步,加速度单位为个元胞/仿真步2)的多值元胞自动机(Burgers Cellular Automaton, BCA)模型。此后又对BCA模型进行了扩展,提出考虑最大速度为2的EBCA (Extended BCA)模型[13],以及考虑高速和长视距的一般化多值元胞自动机模型(GBCA)[14]。
由于交通拥堵问题的加剧,非机动车交通流的研究被越来越多的国内外学者关注[15-19]。同时,有部分学者开始考虑将机动车元胞自动机建模方法应用于非机动车交通流仿真,如张晋等[20]参照机动车元胞自动机模型,建立了单向二维元胞自动机自行车模型;冯雪等[21]以NaSch模型为基础,建立了机非混行交通流模型。由于非机动车道没有明显的车道划分、非机动车运动灵活性高、非机动车换道行为复杂等特点,多值元胞自动机模型更适用于两轮车辆交通仿真。其中,Jia等[22]利用多值元胞自动机模型研究最大速度分别为1和2的两种车型混合的非机动车流;李新刚等[23]为研究三轮车对非机动车流的影响,建立了三轮车(最大速度为1)、快速自行车(最大速度为2)和慢速自行车(最大速度为1)混合的多值元胞自动机交通流模型;贾林等[24]还利用最大速度为2的多值元胞自动机模型研究了非机动车对机动车流的影响。然而,非机动车道中不仅存在最大速度不大于2的人力自行车和三轮车,还存在最大速度大于2的电动自行车,因此,杨晓芳等[25]将多值元胞自动机模型的最大速度拓展为3。
以上研究中的多值元胞自动机模型虽然能模拟含人力自行车和电动自行车的非机动车交通流,但存在以下局限性:(1) 模型中车辆的最大速度不能大于3,且无最大速度不可扩展性,而非机动车道交通流中还包含大量最大速度更高的摩托车流;(2) 当最大速度大于1时,未考虑车辆的加速过程,车辆的最大加速度值被默认为最大速度值,而电动自行车和摩托车是无法在1仿真步(1 s)内从静止加速到最大速度的;(3) 该类模型的随机慢化行为只是对满足移动要求的车辆数减1,这使得随机慢化效果受元胞容量的影响较大;(4) 不同速度车辆的随机慢化概率相同。
本文在EBCA2模型的基础上,对车辆的最大速度进行扩展,并加入车辆的加速过程,最终建立适用于人力自行车、电动自行车和摩托车的多值元胞自动机交通流模型。为更真实地模拟实际交通,模型还改进了随机慢化行为。最后,利用改进模型分别模拟并分析了两轮车的最大速度、最大加速度、以及不同速度车辆的慢化行为对非机动车交通流的影响。
1 模型 1.1 EBCA2模型EBCA模型是Nishinari等[13]将BCA模型扩展成最大速度为2的模型。根据优先行驶权的不同,EBCA模型可分为EBCA1和EBCA2两种形式[26]。在EBCA1模型中,速度为1的车辆具有优先行驶权;在EBCA2模型中,速度为2的车辆具有优先行驶权。本文是在EBCA2模型的基础上进行扩展的,因此主要介绍EBCA2模型。
EBCA2模型的演化过程可分为两步。第1步,如果前面紧邻的两个元胞都有空位,车辆移动到前面第2个元胞上;第2步,如果紧邻元胞还有空位,能向前移动一个元胞的车辆数在除去第1步移动的车辆数后,剩余车辆向前移动1个元胞。EBCA2模型的元胞状态演化方程为[26]:
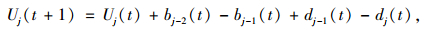
|
(1) |
式中,Uj(t)为时刻t元胞j中的车辆数;bj(t)=min[Uj(t), M-Uj+1(t), M-Uj+2(t)],为能移动两个元胞的车辆数;dj(t)=min{min[Uj(t), M-Uj+1(t)]-bj(t), M-Uj+1(t)-bj-1(t)}为能移动1个元胞的车辆数,其中min (a, b)为在a和b中取较小值,类似地,max (a, b)为在a和b中取较大值;M为元胞容量。虽然EBCA2能对自行车流进行有效的分析,然而其模型的适用范围较窄,且对两轮车辆加速过程的模拟过于简化,无法适用于最大速度大于2的仿真环境。故本文在EBCA2的基础上对多值元胞自动机模型进行改进。
1.2 改进模型改进模型在以下4个方面对EBCA2模型进行改进:(1) 考虑了车辆的加速过程;(2) 随机慢化行为中考虑了随机慢化车辆数;(3) 可实现不同速度车辆以不同随机慢化概率随机慢化;(4) 使模型更加一般化,可适用于最大速度为Vmax的车流仿真。
假设改进模型遵循以下规则:(1) 采取高速车辆优先原则,即高速车辆具有优先行驶权;(2) 在空间条件和速度条件的限制下,车辆以其能达到的最大速度移动;(3) 在同一个仿真步中,移动至元胞(i+1)的车辆来源于移动至元胞i的车辆;(4) 在同一个仿真步中,离开元胞后所腾出的空间不允许其他车辆进入。则改进模型元胞状态的演化方程为:
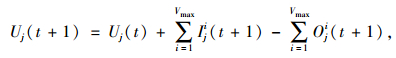
|
(1) |
式中,Iji(t)为时刻t元胞j中以速度i移入的车辆数;Oji(t)为时刻t元胞j中以速度i移出的车辆数,则Iji(t)=Oj-ii(t);Vmax为最大速度。
在考虑加速度的情况下,每个时间步能以速度i移出的车辆数与在速度条件下能以速度i前进的车辆数、在空间条件下能以速度i前进的车辆数、以及已经以速度大于i移出的车辆数有关。所以Oji(t)可表示为:
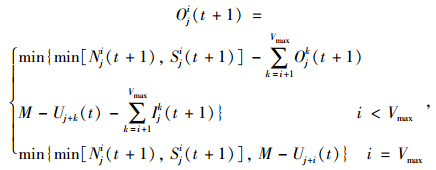
|
(2) |
式中,Ijk(t)为在时刻t元胞j中以速度k移入的车辆数;Ojk(t)为在时刻t元胞j中以速度k移出的车辆数;Sji(t)为在空间限制条件下,时刻t元胞j中最多能移i个元胞的车辆数;Sji(t)为在空间限制条件下,时刻t元胞j中最多能移i个元胞的车辆数;Nji(t)为在时刻t元胞j中能以速度i前进的车辆数。由于车辆的最大加速度为amax,且规则(3)规定车辆以其可达到的最大速度行驶,所以Nji(t+1)=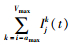
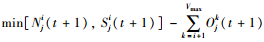
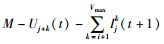
在实际交通中,两轮车的行驶会受到干扰,如体力消耗(对于人力自行车)、路面状况不好、驾驶员心态的变化等,因此需要引入随机慢化行为。贾斌、姜锐等[22, 27]使用多值元胞自动机模型研究非机动车流时,只对速度为2的高速车辆进行了随机慢化,且每个元胞只慢化1辆高速车辆。杨晓芳等[25]在研究人力自行车和电动自行车混行交通流时,将速度为2和3的车辆进行了随机慢化,但其慢化车辆数仍然为每个元胞, 每种车速只慢化1辆车。然而,在非机动车流中,不仅存在靠人力牵引的人力自行车,还存在具备牵引动力的电动自行车和摩托车。电动自行车和摩托车的慢化行为受骑者体力的影响较小,而受环境和驾驶员状态影响较大,所以也存在低速车辆的慢化行为。同时,车辆的慢化行为是相对独立的,故1个元胞内相同车速的慢化车辆数也是随机的。因此,本文将随机慢化规则定义为:以慢化概率pslowi令Oji(t)=rand[0, Oji(t)-1],其中,rand[a, b]为在区间[a, b]之间产生一个随机整数。为避免慢速车辆直接变为静止状态,在计算Oji-1(t)之前需对速度为i的车辆进行随机慢化。
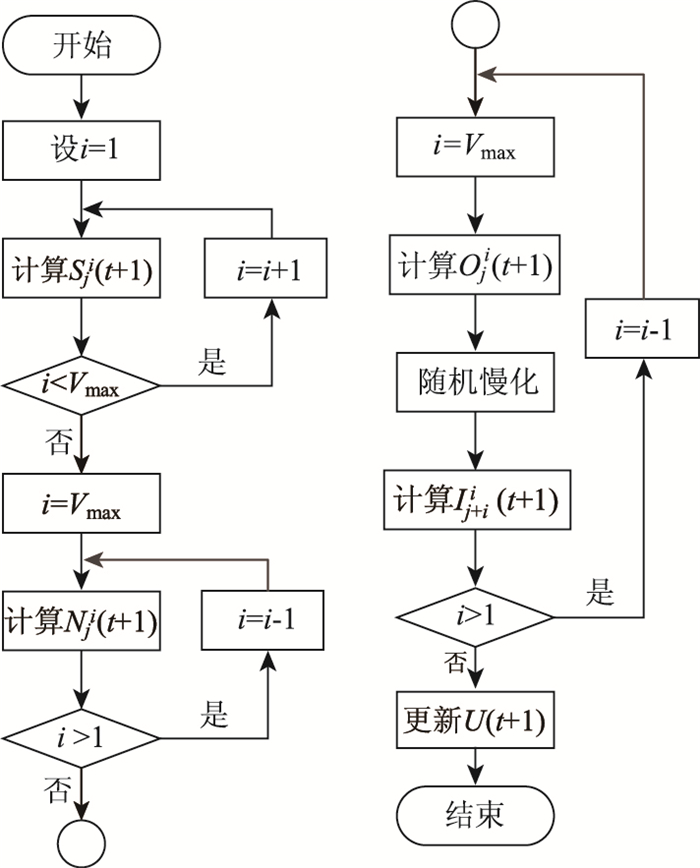
改进模型的计算步骤如图 1所示。
|
| 图 1 改进模型模拟仿真流程图 Fig. 1 Flowchart of simulation with improved model |
| |
2 仿真分析
叶晓飞、曹韦华等[28-29]对两轮车车身长度调查发现,人力自行车、电动自行车和摩托车的平均车身长度分别为1.70, 1.75, 1.80 m。综合考虑调查结果以及车辆间的安全间距,设仿真元胞长度为Lcell=1.9 m。另令仿真空间长度为L=4 000个元胞,车辆占用宽度为1 m,元胞宽度为3 m,即元胞容量为M=3辆车。采用周期边界条件,设仿真步长为1 s, 初始车辆数为N,且在道路上随机分布, Qjcell(t)为时刻t经过元胞j的车辆数,则系统平均流量Q和平均速度V的统计公式为:
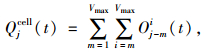
|
(3) |
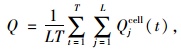
|
(4) |
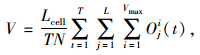
|
(5) |
式中Oj-mi(t)为时刻t元胞j-m中以速度k移出的车辆数。
2.1 改进后模型与EBCA2模型对比分析为分析慢化车辆数、慢化低速车辆和加速过程对交通流的影响,本节以Vmax=2为例,进行4个仿真试验,分别为:(1) 仿真试验1,只考虑慢化车辆数;(2) 仿真试验2,考虑慢化车辆数和慢化低速车辆;(3) 仿真试验3,考虑以上3个因素;(4) 仿真试验4,用EBCA2模型仿真,即以上3个因素都不考虑。其中对比仿真试验3所使用模型即为1.2节中介绍的改进模型。设pslow={pslow1, pslow2, …, pslowVmax}为不同速度车辆的随机慢化概率集合,则以上4个仿真试验模型所对应的描述分别为:
(1)以概率pslowi令Oji(t)=rand[0, Oji(t)-1],pslow={0, 0.1},amax=2;
(2)以概率pslowi令Oji(t)=rand[0, Oji(t)-1],pslow={0.1, 0.1},amax=2;
(3)以概率pslowi令Oji(t)=rand[0, Oji(t)-1],pslow={0.1, 0.1},amax=1;
(4)以概率pslowi令Oji(t)=max[0, Oji(t)-1],pslow={0, 0.1},amax=2。
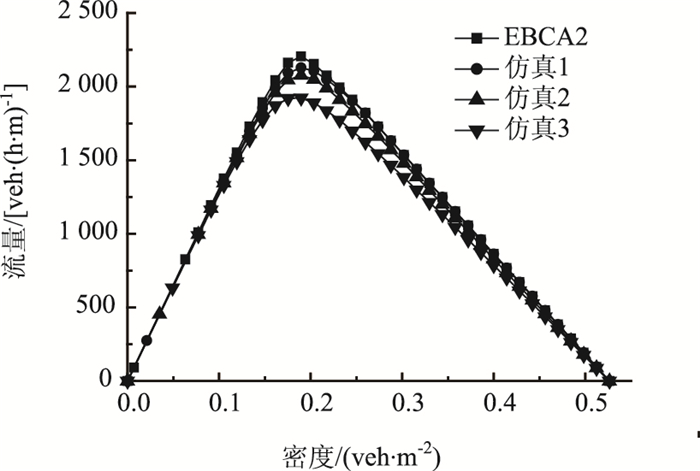
图 2为对比仿真下两轮车的流量-密度关系。可以看出,加速过程、慢化车辆数和低速车辆的随机慢化行为对交通流都会产生一定影响, 其中加速过程对车流影响最大;慢化车辆数对交通流影响次之;而在考虑慢化车辆数的情况下,低速车辆的随机慢化行为对交通流影响相对较小。慢化车辆数对交通流的影响主要在临界密度附近,而低速车辆的随机慢化行为和车辆的加速过程对系统所有密度下的交通流都存在影响,且在临界密度附近和高密度环境下对交通流影响较为明显。因此,在非机动车交通流研究中,建立考虑车辆的加速过程,慢化车辆数和低速车辆慢化的仿真模型,对两轮车辆交通流研究具有重要意义。
|
| 图 2 在不同仿真模型下的流量-密度曲线图 Fig. 2 Relationship between traffic volume and density using different simulation models |
| |
2.2 仿真速度对比分析
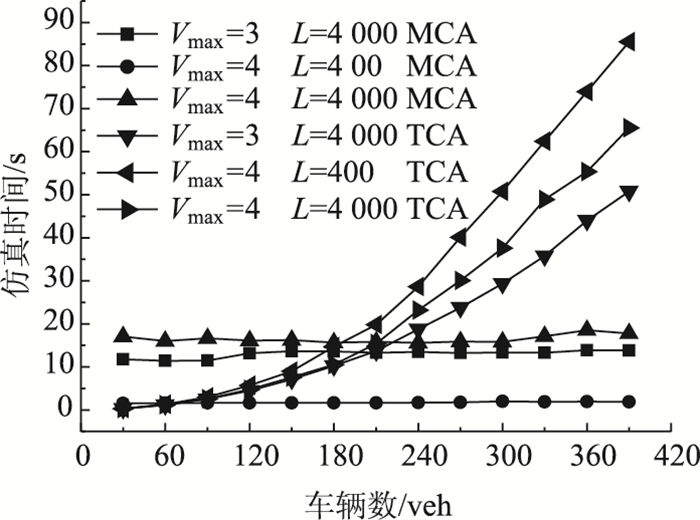
2006年,张晋[20]提出了最大速度为Vmax,加速度为1的非机动车二值元胞自动机(Two-value Cellular Automaton, TCA)模型。为说明本文提出的非机动车多值元胞自动机(Multi-value Cellular Automaton,MCA)模型在仿真速度上的优势,本节将MCA模型和TCA模型进行对比分析。图 3为两种模型在不同仿真环境下的仿真时间关系图。
|
| 图 3 不同模型和不同仿真环境下的仿真时间关系图 Fig. 3 Relationship of simulating times using different models in different simulating environment |
| |
图 3显示,改进的多值元胞自动机模型仿真时间受仿真系统中车辆最大速度、仿真道路长度的影响较大,而受仿真系统中车辆数的影响较小。二值元胞自动机模型仿真时间不仅受仿真系统中仿真道路长度、车辆数的影响,还随系统中车辆密度的增加而急速增加。仿真道路长度为4 000个元胞,车辆最大速度为4时,两种模型的仿真时间曲线相交于车辆数为210辆车附近,即此情况下,仿真密度大于0.008 62 veh/m2时,多值元胞自动机模型的仿真速度更快。而在张晋[20]的非机动车仿真研究中,车辆密度研究间隔为0.01 veh/m2,故在非机动车仿真研究中,尤其在仿真车辆数较多时,多值元胞自动机模型在仿真速度上占绝对优势。
2.3 最大速度影响分析曹韦华[29]对赣州市两轮车的最大速度进行了调查,发现人力自行车、电动自行车和摩托车的最大速度分别为5.9,7.8,11.2 m/s,故本节对两轮车速度分别为3,4,6时的情况进行仿真分析。图 4为两轮车在两种仿真模型(MCA模型和TCA模型)和不同最大速度Vmax={3, 4, 6}情况下的仿真流量-速度-密度关系图。设慢化概率pslow=0,amax=2,由于当pslow=0时,多值元胞自动机模拟存在多重状态,即在不同的初始状态会产生不同的稳态,故本文取最常见的分支情况进行分析。
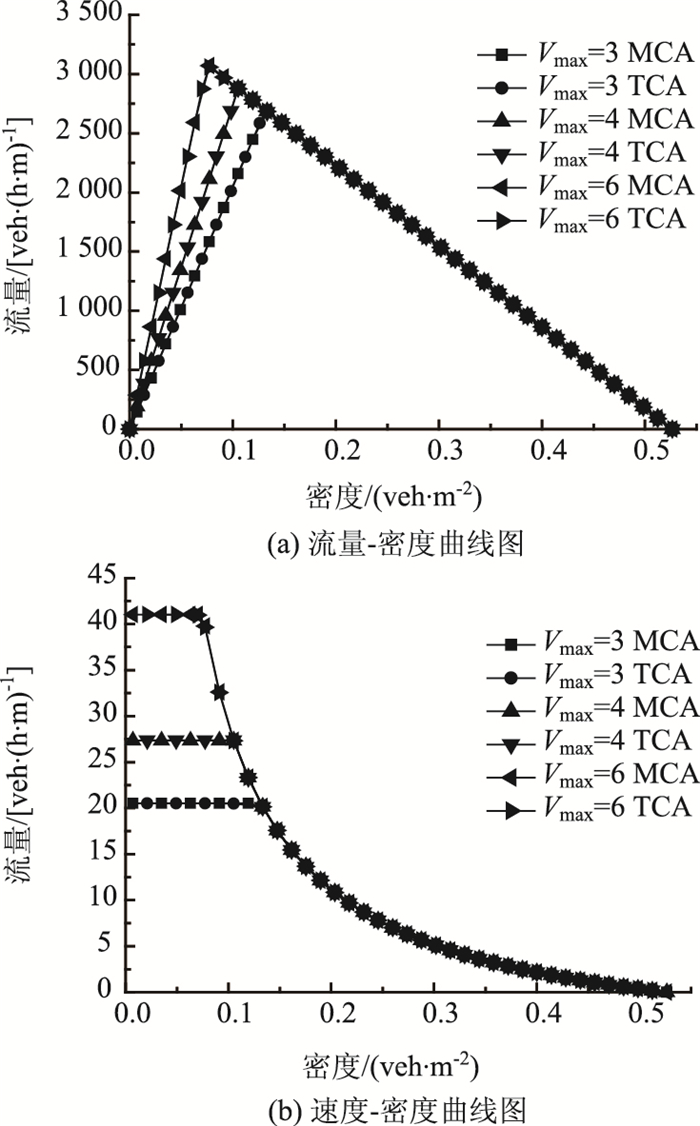
|
| 图 4 两轮车在不同最大速度下仿真的流量-速度-密度关系图 Fig. 4 Relationships of traffic volume, velocity and density of two-wheel vehicle at different maximum velocities by simulation |
| |
从图 4可以看出,在最大速度相同时,非机动车TCA模型和MCA模型的系统平均流量-密度曲线和平均速度-密度曲线都几乎重合。这说明,改进的MCA模型和TCA模型在系统平均流量和系统平均速度上无显著差异,即改进模型在提高仿真速度的同时,保证了非机动车流的流量-密度-速度特性不受影响。
此外还可以发现,系统自由流状态下的流量-密度曲线斜率随系统车辆最大速度的增加而增加;而拥堵流状态下,流量-密度曲线斜率不受系统最大速度变化的影响,且速度与密度呈负相关。交通流流量-速度-密度关系模型为[30]:Q=KV,故dQ/dK=V+KdV/dK,式中Q为系统平均流量,K为系统平均密度,V为系统平均速度。在自由流状态下,由于速度恒为最大速度Vmax,故dQ/dK=Vmax,即流量曲线斜率为Vmax,且随车辆最大速度的增加而线性增加。
从图 5可以看出,在阻塞流状态下,系统处于经过元胞的车流量与元胞中车辆数关于元胞容量互补的稳态,且流量-密度关系的曲线斜率为-3 600/LM。故当pslow=0时,流量-密度关系只与仿真道路宽度和长度有关,而与车辆的最大速度无关。设自由流的流量-密度曲线函数为Qf=VmaxK,其中Qf为自由流流量。令f=3 600/LM,则阻塞流的流量-密度曲线函数为Qc=f(Kj-K),其中Qc为阻塞流流量;Kj为阻塞密度。另设Qm为峰值流量,则当密度为临界密度Kc时,Qf=Qc=Qm,即Kc=Kjf/(Vmax+f),Qm=KcVmax=Kjf-Kjf2/(Vmax+f)。故峰值流量和临界密度与最大速度成负相关,即峰值流量随最大速度的增加而增加,临界密度随最大速度的增加而减小。同时在阻塞流状态,V=Q/K=Kjf/K-f,即速度与密度成负相关。
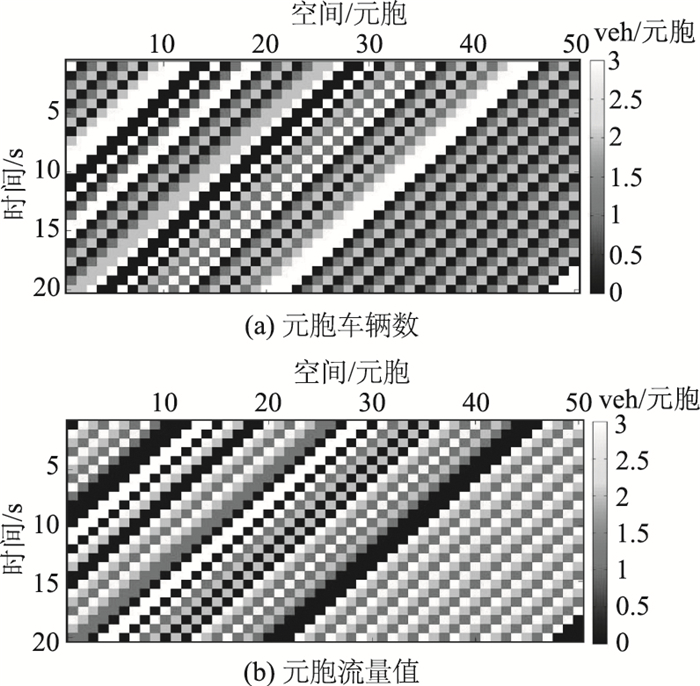
|
| 图 5 在pslow=0, Vmax=2,K=0.07下仿真的时空图 Fig. 5 Space-time diagrams when pslow=0, Vmax=2, and K=0.07 by simulation |
| |
2.4 最大加速度影响分析
曹韦华[29]对赣州两轮车的加速性能进行调查后发现,人力自行车、电动自行车和摩托车的最大加速度分别为2,2.87,3.54 m/s2,因此,本节对两轮车加速度分别为1和2时的非机动车流进行仿真研究。图 6为两轮车在不同最大加速度下仿真的流量-速度-密度关系。设Pslow={0.1, 0.1},Vmax=6。从图 3可以看出,加速度从1变为2,不仅对系统的最大流量有影响(上升了15.2%),而且对拥堵流状态的流量影响显著。因此,当非机动车道车流密度大于0.06 veh/m2时,可考虑对加速度差值较大的车种进行分流处理,从而增强非机动车道的通行能力。
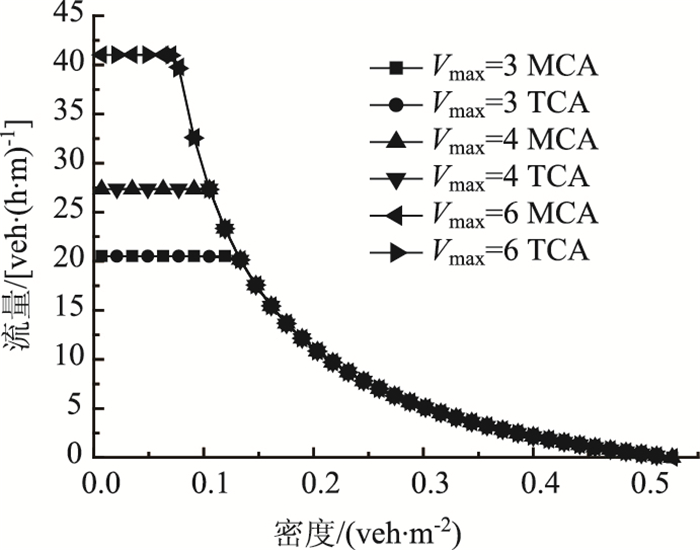
|
| 图 6 两轮车在不同最大加速度下仿真的流量-密度关系图 Fig. 6 Relationship between traffic volume and density at different maximum accelerations by simulation |
| |
2.5 随机慢化行为对不同速度车辆的影响分析
随机慢化行为指由于道路环境、驾驶员状态和车辆性能等不确定性因素而导致的车辆慢化行为。为分析不同速度的随机慢化行为对系统交通流的影响,对随机慢化规则进行修改:速度为i(i=1, 2, …,V)的车辆以概率pslowi随机慢化。本节分别以人力自行车(Vmax=3, amax=1)、电动自行车(Vmax=4, amax=1)和摩托车(Vmax=6, amax=2)为例,对不同速度的车辆受随机慢化行为的影响进行分析。
图 7为3种两轮车在不同混合慢化概率情况下仿真的流量-密度关系。可以发现,速度为1的车辆的随机慢化行为对amax=1的自行车和电动自行车影响显著,且流量降幅大、受影响密度范围广;而速度为1的车辆的随机慢化行为对摩托车的影响较小,仅仅是密度较大的阻塞流受到了较小的影响。速度为2的车辆的随机慢化行为对3种两轮车的影响都相对显著,其中自行车和电动自行车所受影响比摩托车的更大。影响自由流流量-密度曲线斜率的随机慢化行为包括:速度为Vmax和速度为Vmax-1的车辆的人力自行车和电动自行车的随机慢化行为、以及速度为Vmax的摩托车的随机慢化行为。总体而言,不同速度的随机慢化行为对非机动车交通流的影响不同,且最大加速度为2的摩托车受随机不同速度慢化行为的影响最小。
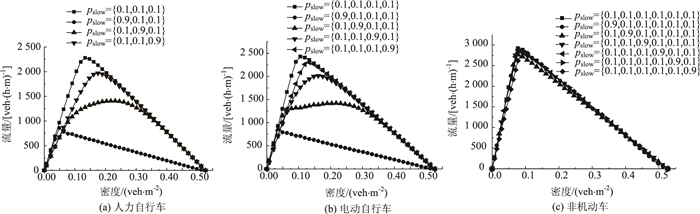
|
| 图 7 两轮车在不同慢化概率混合情况下仿真的流量-密度关系图 Fig. 7 Relationship of traffic flow and density under different mixed stochastic deceleration by simulation |
| |
3 结论
本文在EBCA2模型的基础上,对车辆的最大速度进行了扩展,并加入了车辆的加速过程,最终建立了适用于人力自行车、电动自行车和摩托车的多值元胞自动机交通流模型。为更真实地模拟实际交通,在模型中加入了改进的随机慢化行为。最后,利用新模型分别模拟分析了最大速度、最大加速度、不同速度车辆的慢化行为对交通流的影响。仿真结果表明:(1) 车辆的加速过程、慢化车辆数和低速车辆慢化行为对系统交通流都会产生一定影响,其中,车辆的加速过程对非机动车交通流影响最大;(2) 与非机动车两值元胞自动机模型相比,改进模型在保证其在车流的流量-密度-速度特性不受影响的情况下,大大增加了仿真速度;(3) 峰值流量和临界密度与两轮车的最大速度成反相关。在自由流状态下,流量曲线斜率为Vmax,而在阻塞流状态下,流量-密度曲线斜率由元胞长度和元胞容量决定,与两轮车的最大速度无关;(4) 当非机动车道车流密度大于0.06 veh/m2时,加速度的变化对交通流影响较大,可考虑对摩托车与其他车种进行分流处理,从而增强非机动车道的通行能力;(5) 不同速度下的随机慢化行为对交通流的影响不同,且最大加速度为2的摩托车的随机慢化行为所受影响较小。
未来研究方向是:(1) 精细化多值元胞自动机模型。考虑1辆车纵向占用多个元胞的情况,以更精准地区分人力自行车、电动自行车和摩托车的最大仿真加速度。(2) 考虑多车种混行的多值元胞自动机模型,如摩托车、人力自行车与电动自行车混行,摩托车与三轮车混行等。
| [1] | RICHARDS P I. Shock Waves on the Highway[J]. Operations Research , 1956, 4 (1) : 42-51 |
| [2] | JIANG R, WU Q, ZHU Z. A new dynamics model for traffic flow[J]. Chinese Science Bulletin , 2001, 46 (4) : 345-348 |
| [3] | PRIGOGINE I, HERMAN R. Kinetic Theory of Vehicular Traffic[R]. New York:Elsevier, 1971. |
| [4] | PAVERI-FONTANA S L. On Boltzmann-like Treatments for Traffic Flow:A Critical Review of the Basic Model and an Alternative Proposal for Dilute Traffic Analysis[J]. Transportation Research , 1975, 9 (4) : 225-235 |
| [5] | ZHAO X, GAO Z. A Control Method for Congested Traffic Induced by Bottlenecks in the Coupled Map Car-following Model[J]. Physica A:Statistical Mechanics and Its Applications , 2006, 366 : 513-522 |
| [6] | 陈漩, 高自友, 赵小梅, 等. 反馈控制双车道跟驰模型研究[J]. 物理学报 , 2007, 56 (4) : 2024-2029 CHEN Xuan, GAO Zi-you, ZHAO Xiao-mei, et al. Study on the Two-lane Feedback Controlled Car-following model[J]. Acta Physica Sinica , 2007, 56 (4) : 2024-2029 |
| [7] | 江欣国, 夏亮. 基于元胞自动机的高速公路临时瓶颈交通流仿真[J]. 西南交通大学学报 , 2016, 51 (1) : 128-137 JIANG Xin-guo, XIA Liang. Simulation of Temporary Traffic Bottleneck on Highways Based on Cellular Automaton[J]. Journal of Southwest Jiaotong University , 2016, 51 (1) : 128-137 |
| [8] | 赵康嘉, 陈淑燕.基于元胞自动机的交通事件交通流仿真模型[J].公路交通科技, 2014, 31(3):133-138. ZHAO K, CHEN S, LAO Y. Cellular Automaton Based Traffic Flow Simulation Model for Traffic Incidents[J]. Journal of Highway and Transportation Research and Development, 2014, 31(3):133-138. http://manu12.magtech.com.cn/Jweb_gljtkj/CN/abstract/abstract14321.shtml |
| [9] | NAGEL K, SCHRECKENBERG M. A Cellular Automaton Model for Freeway Traffic[J]. Journal de Physique I , 1992, 2 (12) : 2221-2229 |
| [10] | 郑英力, 翟润平, 马社强. 交通流元胞自动机模型综述[J]. 公路交通科技 , 2006, 23 (1) : 110-115 ZHENG Yin-li, ZHAI Run-ping, MA She-qiang. Survey of Cellular Automata Model of Traffic Flow[J]. Journal of Highway and Transportation Research and Development , 2006, 23 (1) : 110-115 |
| [11] | KAI N, WOLF D E, WAGNER P, et al. Two-lane Traffic Rules for Cellular Automata:A systematic Approach[J]. Physical Review E:Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics , 1997, 58 (2) : 1425-1437 |
| [12] | NISHINARI K, TAKAHASHI D. Analytical Properties of Ultradiscrete Burgers Equation and Rule-184 Cellular Automaton[J]. Journal of Physics A:Mathematical and General , 1998, 31 (24) : 5439-5450 |
| [13] | NISHINARI K, TAKAHASHI D. A New Deterministic CA Model for Traffic Flow with Multiple States[J]. Journal of Physics A:Mathematical and General , 1999, 32 (1) : 93-104 |
| [14] | MATSUKIDAIRA J, NISHINARI K. Euler-Lagrange Correspondence of Cellular Automaton for Traffic-Flow Models[J]. Physical review letters , 2003, 90 (8) : 137-168 |
| [15] | TANG T Q, HUANG H J, SHANG H Y. A Macro Model for Bicycle Flow and Pedestrian Flow with The Consideration of The Honk Effects[J]. International Journal of Modern Physics B , 2011, 25 (32) : 4471-4479 |
| [16] | HOSSAIN M, MCDONALD M. Modelling The Impacts of Reducing Non-Motorised Traffic in Urban Corridors of Developing Cities[J]. Transportation Research Part A:Policy and Practice , 1998, 32 (4) : 247-260 |
| [17] | 林贵宝, 马荣国, 杨泞珲. 机非划线分割道路自行车交通流对机动车运行的影响[J]. 公路交通科技 , 2016, 33 (1) : 112-118 LIN Gui-bao, MA Rong-guo, YANG Ning-hui. Impact of Bicycle Traffic on Vehicle Operation on Divided Road[J]. Journal of Highway and Transportation Research and Development , 2016, 33 (1) : 112-118 |
| [18] | 南天伟, 毛保华, 陈志杰, 等.基于元胞自动机的城市混合非机动车流特性模拟研究[J].公路交通科技, 2014, 31(1):104-109. NAN Tian-wei, MAO Bao-hua, CHEN Zhi-jie, et al. Urban Mixed Non-motor Vehicle Flow Character Simulation Based on Cellular Automata[J]. 2014, 31(1):104-109. http://manu12.magtech.com.cn/Jweb_gljtkj/CN/abstract/abstract14295.shtml |
| [19] | 张之勇, 郭孜政, 姚磊. 基于云模型的非机动车交通流速度仿真[J]. 公路交通科技 , 2015, 32 (11) : 126-131 ZHANG Zhi-yong, GUO Zi-zheng, YAO Lei. Simulation of Traffic Flow Speed of Non-motorized Vehicle Based on Cloud Model[J]. Journal of Highway and Transportation Research and Development , 2015, 32 (11) : 126-131 |
| [20] | 张晋, 王慧, 李平. 基于元胞自动机(CA)的自行车流建模及仿真[J]. 公路交通科技 , 2006, 23 (1) : 125-129 ZHANG Jin, WANG Hui, LI Ping. Bicycle Flow Modeling and Simulation Based on Cellular Automaton[J]. Journal of Highway and Transportation Research and Development , 2006, 23 (1) : 125-129 |
| [21] | 冯雪, 王喜富. 考虑自行车流特性的机非混合交通流元胞自动机仿真[J]. 公路交通科技 , 2016, 33 (3) : 132-137 FEN Xue, WANG Xi-fu. Simulation of Mixed Traffic Flow by Cellular Automaton Considering Bicycle Flow Characteristics[J]. Journal of Highway and Transportation Research and Development , 2016, 33 (3) : 132-137 |
| [22] | JIA B, LI X G, JIANG R, et al. Multi-Value Cellular Automata Model for Mixed Bicycle Flow[J]. The European Physical Journal B , 2007, 56 (3) : 247-252 |
| [23] | 李新刚, 高自友, 赵小梅, 等. 混合非机动车流的多值元胞机模型模拟研究[J]. 物理学报 , 2008, 57 (8) : 4777-4785 LI Xin-gang, GAO Zi-you, ZHAO Xiao-mei, et al. Multi-value Cellular Automata Model for Mixed Non-motorized Traffic Flow[J]. Acta Physica Sinica , 2008, 57 (8) : 4777-4785 |
| [24] | 贾宁, 马寿峰. 自行车干扰下机动车交通流的元胞自动机模型[J]. 系统工程理论与实践 , 2010, 30 (7) : 1333-1339 JIA Ning, MA Shou-feng. Cellular Automaton Model for the Motor-vehicle Flow under the Interference of Bicycles[J]. Systems Engineering-Theory & Practice , 2010, 30 (7) : 1333-1339 |
| [25] | 杨晓芳, 牛兆雨, 王建蓉. 基于多值元胞机的混合非机动车通行能力研究[J]. 系统仿真学报 , 2012, 24 (12) : 2577-2581 YANG Xiao-fan, NIU Zhao-yu, WANG Jian-rong. Mixed Non-Motorized Traffic Flow Capacity Based on Multi-value Cellular Automata Model[J]. Journal of System Simulation , 2012, 24 (12) : 2577-2581 |
| [26] | NISHINARI K, TAKAHASHI D. Multi-Value Cellular Automaton Models and Metastable States in A Congested Phase[J]. Journal of Physics A:Mathematical and General , 2000, 33 (43) : 7709 |
| [27] | JIANG R, JIA B, WU Q S. Stochastic Multi-value Cellular Automata Models for Bicycle Flow[J]. Journal of Physics A:Mathematical and General , 2004, 37 (6) : 2063 |
| [28] | 叶晓飞, 陈峻, 顾姗姗. 城市道路路段电动自行车相对于自行车的换算系数[J]. 公路交通科技 , 2012, 29 (10) : 109-116 YE Xiao-fei, CHEN Jun, GU Shan-shan. Conversion Coefficient of Electric-bike into Bicycle on Urban Road Section[J]. Journal of Highway and Transportation Research and Development , 2012, 29 (10) : 109-116 |
| [29] | 曹韦华.基于元胞自动机的两轮车流建模与仿真[D].赣州:江西理工大学, 2015. CAO Wei-hua. Modeling and Simulation of Mixed Two Wheels Traffic Flow Based on Cellular Automata[D].Ganzhou:Jiangxi University of Science and Technology, 2015. |
| [30] | 李江. 交通工程学[M]. 北京: 人民交通出版社, 2002 . LI Jiang. Traffic Engineering[M]. Beijing: China Communications Press, 2002 . |
 2017, Vol. 34
2017, Vol. 34
