扩展功能
文章信息
- 冯玉荣, 杨少伟, 张驰, 陈通
- FENG Yu-rong, YANG Shao-wei, ZHANG Chi, CHEN Tong
- 高速公路交织区服务水平敏感性分析
- Analysis on Service Level Sensitivity of Expressway Weaving Section
- 公路交通科技, 2017, 34(1): 103-111
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 103-111
- 10.3969/j.issn.1002-0268.2017.01.015
-
文章历史
- 收稿日期: 2016-05-17
2. 西安公路研究院, 陕西 西安 710054
2. Xi'an Highway Institute, Xi'an Shaanxi 710054, China
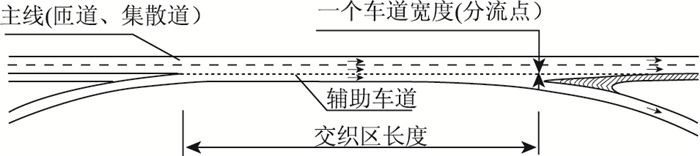
交织是指两个或者多个方向车流在一定长度路段不借助交通控制设备(除引导标志)向同一方向行驶形成的车流相交现象。因此,当汇合车流后面紧接着分散车流就会形成交织区,“紧跟”是指在合流与分流之间没有足够的距离使其独立行驶[1]。我国高速公路交织区主要存在位置如图 1所示。
|
| 图 1 高速公路交织区 Fig. 1 Weaving sections of expressway |
| |
服务水平是指驾驶员感受公路交通流运行状态的质量指标,通常用平均行驶速度、行驶时间、驾驶自由度和交通延误等指标表征。美国在《道路通行能力手册》(HCM2010)中将服务水平划分为A~F共6个等级,服务水平评价指标采用密度;德国《道路通行能力手册》(HBX2015)对服务水平的评价采用负荷率,即规划或实际交通量与设施通行能力之比,根据负荷率的不同将服务水平划分为A~F共6个等级[2];我国在《公路工程技术标准》(JTG B01-2014)中用饱和度来衡量拥挤程度,同时采用小客车实际行驶速度与自由流速度之差作为次要评价指标,将服务水平分为6级[3]。由于交织车辆在交织区长度范围内需要强制性变换车道进入期望出入口,交织区的交通变道行为高于基本路段,驾驶员在交织区的驾驶质量感受忍耐度更高,所以各国对交织区服务水平评价指标的阈值比基本路段高一些。
服务水平评价离不开道路通行能力的分析计算,现有交织区服务水平评价通过直接或间接计算交织区通行能力完成。目前,交织区通行能力的研究方法包括美国《道路通行能力手册》分析法[4-5]、数学理论计算法[6-10]和计算机模拟分析法[11-17],其中以美国《道路通行能力手册》分析法应用较为广泛。
我国对高速公路交织区的研究主要参照美国《道路通行能力手册》中的研究方法,编制了《公路通行能力手册》[18]。首先,该手册中使用的调查数据量少、陈旧且较分散,随着我国道路交通条件的变化,车辆在交织区内的交通运行状况发生了变化;其次,该手册仅提供不同交织构型、不同流量比、车道数和交织区长度的通行能力值,未提供通行能力的计算模型;第三,未定量分析交织区影响因素对交织运行的敏感性。
本文以西安绕城高速公路吕小寨立交-朱宏路立交之间交织区为调查对象,收集交织区道路条件和交通流数据,根据我国交织区实际运营现状修正HCM2010速度预测模型,对公式系数进行标定,对公式形式进行验证,通过设计试验方案,进行影响因素对交织区通行能力和服务水平的敏感性分析。
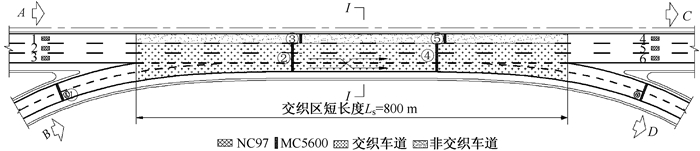
1 交织区数据收集与分析交织区数据的收集是为分析交织区的交通流特性、交织区的交通运行影响因素和标定HCM2010速度预测模型提供依据。本文选取西安绕城高速公路吕小寨立交-朱宏路立交之间交织区为调查对象,收集交织区的道路条件和交通流数据。调查时间为2015年1月18日6:00-12:00(非节假日)。交织区平面尺寸和仪器设备布设如图 2所示。
|
| 图 2 交织区几何尺寸及仪器布设示意图 Fig. 2 Schematic diagram of weaving section geometry and equipment layout |
| |
需要说明的是,通过对陕西省高速公路路网中存在的交织区相关数据收集和分析发现,西安绕城高速公路吕小寨立交-朱宏路立交之间的交织区在道路几何尺寸、交织区几何特征、交通流特性及交通组成等方面具有典型性,所以选取该交织区进行运行分析具有参考意义。再者,本文选取非节假日为调查时段,交通流特性也具有普遍适用性。
通过交通数据采集仪MC5600和磁感应交通流计数器NC97组合的调查方式进行交通流数据采集,交织区入口、出口及交织区段采用MC5600进行数据采集,主线入口和出口分别采用NC97设备进行数据采集。其中NC97采集数据间隔为15 min,获取交织区该时段内的速度、总流量、平均车头时距,不同车型的车流量、交通流量为小客车当量值,各车型车辆折算系数采用《公路工程技术标准》(JTG B01-2014)中规定的换算值。参照HCM2010中关于交织区相关参数的定义,结合该交织区道路和交通参数的调查结果得出下列数据。
(1)道路参数:双向6车道高速公路,设计速度120 km/h,路基宽度34.5 m;
(2)交织区几何特征:交织构型为同侧交织区,交织区内车道数N为4,交织车道数Nw为30,交织区短距离Ls为800 m,进口匝道到主线车流最少变道数为1,主线到出口匝道车流最小变道数为0,变道1次或无需变道就能完成交织行为的车道数Nwl为3;
(3)交通流量:主线至主线(A-C)交通量为Vff,主线至匝道(A-D)交通量为Vfr,匝道至主线(B-C)交通量为Vrf,匝道至匝道(B-D)交通量为Vrr,则交织流量为Vw=Vfr+Vfr,交织区内总流量为V=Vff+Vfr+Vrf+Vrr,交织流量比为VR=Vw/V;
(4)交通组成:小客车80.5%,中型车8.7%,大型车3.6%,汽车列车7.2%。
(5)速度:交织区交织速度和非交织速度通过MCReport和HDM处理软件获取,自由流速度是交通量很小的条件下小客车的平均速度,经测定为80.08 km/h;交织车辆最小速度取24 km/h。
2 HCM2010速度预测模型的修正 2.1 HCM2010速度预测模型HCM2010在理论和回归模型的基础上建立了交织区如下预测模型:总变道率模型、平均速度和稳定情况下的非交织车辆模型(即不在服务水平LOS F上运行)、理想及一般情况下的通行能力模型和交织最长距离模型。其中交织车速和非交织车速的预测模型如下:
(1)交织车辆平均速度
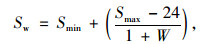
|
(1) |
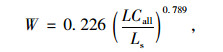
|
(2) |
式中,Sw为交织车辆平均速度;Smax为交织车辆最大预测速度;Smin为交织车辆最小预测速度; LCall为交织区内所有车辆的总变道率; Ls为应用短距离测得的交织区长度; W为交织强度系数。
(2)非交织车辆平均速度
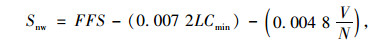
|
(3) |
式中,Snw非交织车辆平均速度;FFS为交织区上游或下游基本路段的自由流速度;LCmin为交织车辆完成交织的最小变道率;V为交织区内总需求流率;N为交织区车道数。
本论文直接运用HCM2010的研究成果。交织区运行分析方法的流程、参数定义和取值详见文献[1]相关规定。
2.2 模型的修正与分析HCM2010速度预测回归模型以美国现已运营的交织区为调查对象,以大量的实测数据为基础,加入了一些自HCM2000出版以来所完成的研究项目中提取出的内容,经统计回归得到速度预测模型。由于我国道路建设标准、交通管理方式、交通运行环境和驾驶员行为特征与美国不尽相同,且有国内学者对HCM2010交织区通行能力分析方法进行了适用性研究,结果表明HCM2010对非交织车速计算存在重复折减[19]。因此需要根据我国交织区的实际运营现状修正HCM2010速度预测模型,对公式系数进行标定,对公式形式进行验证,以保证修正后的速度预测模型适用于我国高速公路交织区的道路交通条件,便于交织区交通运行分析。
由HCM2010交织区长度定义可得交织运行最大交织长度Lmax为:
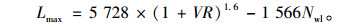
|
(4) |
根据调查时段的交织流量比和变道1次或无需变道就能完成交织行为的车道数Nwl,计算最大交织长度值介于1 006~1 576 m,明显大于实际交织区长度800 m,车辆处于交织运行状态,故本案例按照交织区(不是分离的合流和分流区)来运行分析。
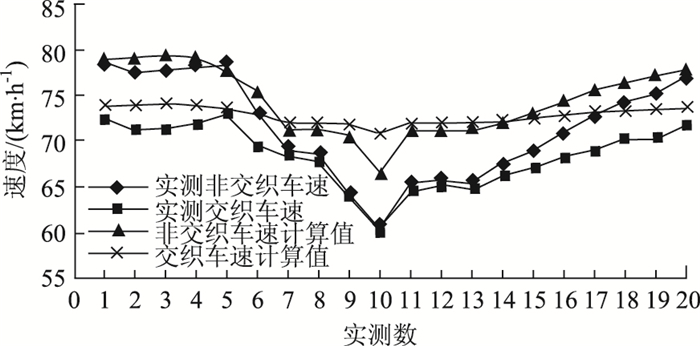
采用HCM2010交织区通行能力运行分析方法计算实测交通流条件下的交织和非交织平均速度,如图 3所示。
|
| 图 3 未修正速度模型交织区速度比较 Fig. 3 Comparison of velocities in weaving sections obtained by unmodified velocity model |
| |
由图 3可知,HCM2010交织车辆速度预测值高于实测值,最大误差为13.95%;非交织车量速度预测值高于实测值,最大误差为16.48%。交织车流速度与非交织车流速度预测值的差值较实测值小,且随交织流量的增加,车速的降低值较实测值小。基于以上判断,针对性地提出交织区车流预测和非交织车流预测修正模型。
(1)交织区车流和非交织车流速度预测模型的修正
交织区车流速度预测修正模型:
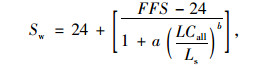
|
(5) |
非交织车流速度预测修正模型:
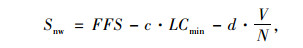
|
(6) |
式中最小交织车速a,b,c,d为标定参数。
依据HCM2010的规定,交织区交织车辆最大预测速度为交织区上游或下游基本路段的自由流速度FFS。用20组现场实测数据对速度预测模型中的a,b,c,d进行标定,标定结果如表 1所示。
| a | b | c | d | R2 | |
| Sw | 0.068 8 | 1.901 | - | - | 0.942 |
| Snw | - | - | 0.003 92 | 0.018 73 | 0.993 |
经回归统计分析,交织车速和非交织车速的相关系数值分别为0.942和0.993,拟合优度较高,表明回归模型对样本数据点拟合程度好。
(2)交织区车流和非交织车流速度预测修正模型的验证
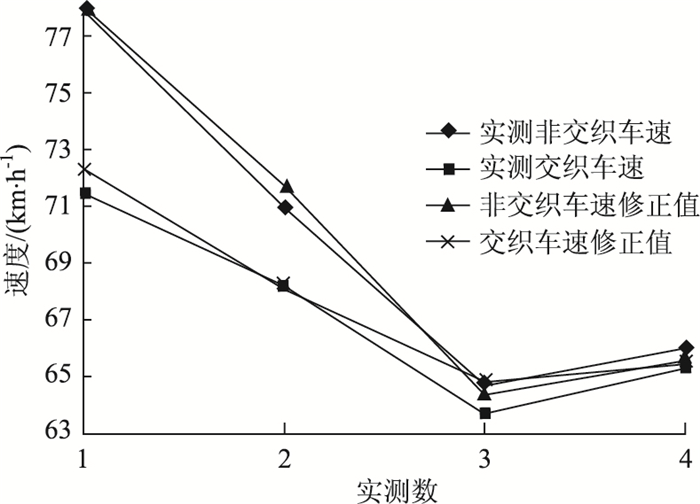
利用剩余的4组调查数据验证修正模型的精度,HCM2010交织车辆速度修正值与实测值的最大误差为1.73%,非交织车量速度修正值与实测值的最大误差为1.06%。计算误差控制在5%之内,表明修正模型具有较高的精度,如图 4所示。
|
| 图 4 修正速度模型验证 Fig. 4 Validation of modified velocity model |
| |
3 交织区影响因素敏感性分析 3.1 试验设计
基于修正后的速度预测模型,交织区影响因素参数取值在其真值范围内,改变某个影响因素取值范围,其他所有参数按原调查数据取值,利用Visual Basic6.0语言开发交织区运行分析计算工具,计算交织区运行效率指标值,分析各影响因素对通行能力和服务水平之间的敏感性。本次试验设计选取11:00-12:00时间段的交通流调查数据。试验设计方案如表 2所示。
| 试验方案 | 试验参数 | 初值 | 终值 | 步长 | 备注 | |
| 1 | 交通 流参数 | Vff/(pcu·h-1) | 1 200 | 4 200 | 300 | 每组试验 仅按该组 初值、终值 和步长进行,其 余道路及交 通流参数 不变 |
| 2 | Vfr/(pcu·h-1) | 0 | 2 800 | 200 | ||
| 3 | Vrf/(pcu·h-1) | 0 | 2 000 | 200 | ||
| 4 | Vrr/(pcu·h-1) | 0 | 2 000 | 200 | ||
| 5 | FFS(km·h-1) | 60 | 120 | 10 | ||
| 6 | 道路 参数 | Ls/m | 100 | 1 600 | 100 | |
| 7 | N/条 | 3 | 5 | 1 |
(1)交通流量取值:交织区各流向交通量的初值和终值根据实测时间段的交通流量变化范围,综合考虑交织区主线和匝道的通行能力选取;
(2)自由流速度根据实测小客车运行速度范围以10 km/h步长由60 km/h调整至120 km/h;
(3)交织区长度初值取100 m,终值取交织运行最大交织长度Lmax=1 600 m,步长取100 m;
(4)交织区车道数3车道调整至5车道,步长为1个车道。
需要说明的是,首先本次试验设计选取11:00-12:00时间段的交通调查数据,对该交织区进行交通优化设计时,本文选取交通紊乱严重的时间段进行敏感性分析,该时间段的交通量特性、速度特性和车头间距特性具有典型性,当交织区内发生交通拥堵时进行匝道交通流控制,可通过控制出入口交通流来调整交织区瓶颈内的实际车流驶入率和最优驶出率,所以对交织运行的敏感性分析以选取的高峰流量时间段交通流量为基准。其次对该交织区进行交通优化设计,通过增加交织区车道数、提高交织区自由流速度和增长交织区长度等措施,缓解交织区交通瓶颈,所以交织区的自由流速度、长度和车道数也以现状调查值为基准。
3.2 敏感性分析(1)方案1:对主线-主线交通需求量的敏感性分析
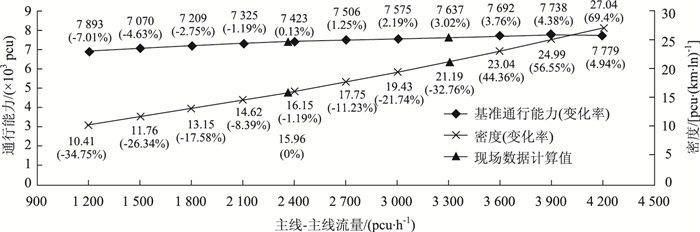
由图 5可知,主线-主线需求量的变化对交织区通行能力和密度的影响基本呈线性增大,在调查时段其余参数不变的情况下,交织区通行能力由密度确定,密度达到27 pcu/(km·ln)时主线-主线需求量为4 200 pcu,交织区通行能力变化幅度较小,变化范围为-7.01%~4.94%,密度变化范围为-34.75%~69.4%。由此说明,主线-主线需求量对交织区运行具有较小敏感性。
|
| 图 5 主线-主线需求量敏感性曲线 Fig. 5 Curves of sensitivity of main line to main line demand |
| |
(2)方案2:对主线-匝道交通需求量的敏感性分析
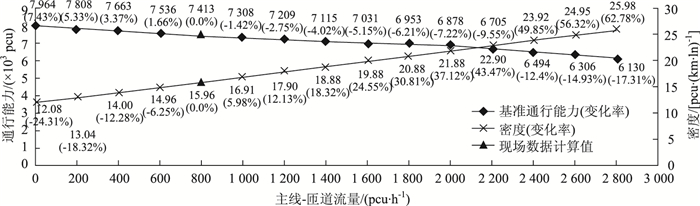
由图 6可知,主线-匝道需求量的变化对交织区通行能力呈线性降低、对密度影响基本呈线性增加。在调查时段其余参数不变的情况下,主线-匝道需求量在0~2 000 pcu之间时交织区通行能力由密度确定,交织区通行能力变化率较小,变化幅度为-7.22%~7.43%,相应密度变化范围为-24.31%~37.12%;主线-匝道需求量在2 000~2 800 pcu之间时,交织区通行能力由交织需求流确定,交织区通行能力变化率较大,变化幅度为-17.31%~-7.22%,相应密度变化范围为37.12%~62.78%。由此说明,主线-匝道需求量对交织区运行具有敏感性。
|
| 图 6 主线-匝道需求量敏感性曲线 Fig. 6 Curves of sensitivity of main line to ramp demand |
| |
(3)方案3:对匝道-主线交通需求量的敏感性分析
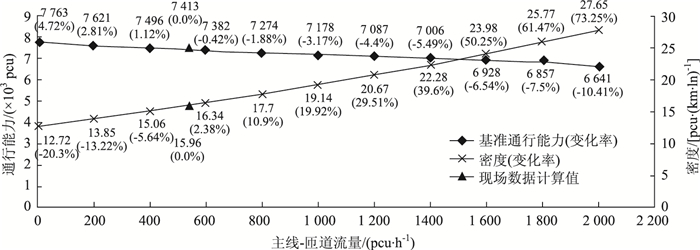
由图 7可知,匝道-主线需求量的增加对交织区通行能力的影响呈线性降低,对密度的影响基本呈线性增加。在调查时段其余参数不变的情况下,匝道-主线需求量在0~1 800 pcu之间时交织区通行能力由密度确定,匝道-主线需求量在1 800~2 000 pcu之间时基准通行能力由交织需求流确定,即最大服务交通量为900 pcu/(h·ln),交织区通行能力的变化范围为-10.41%~4.47%,密度变化范围为-20.3%~73.25%。随着匝道-主线需求量的增加,变道行为更加频繁,对干道直行车流的干扰也会增多,使得交织区的性能降低,当匝道-主线需求量达到1 800 pcu时,交织区通行能力由密度确定转化为由交织需求流确定。由此说明,匝道-主线需求量对交织区运行具有敏感性。
|
| 图 7 匝道-主线需求量敏感性曲线 Fig. 7 Curves of sensitivity of ramp to main line demand |
| |
(4)方案4:对匝道-匝道交通需求量的敏感性分析
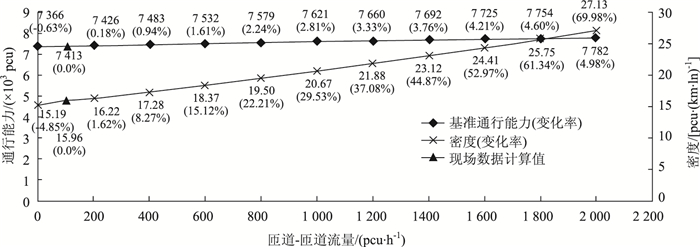
由图 8可知,匝道-匝道需求量的变化对交织区通行能力影响较小,基本呈线性变化。该交织区在调查时段其余参数不变的情况下,交织区通行能力由密度决定,密度达到27 pcu/(km·ln)时匝道-匝道需求量为2 000 pcu,密度变化幅度为74.83%。由于匝道-匝道交通需求对交织运行不利影响较小,但密度增幅较大是由匝道-匝道交通需求的增加引起的,说明匝道-匝道需求量对交织区运行状况的敏感性较小的分析是合理的。
|
| 图 8 匝道-匝道需求量敏感性曲线 Fig. 8 Curves of sensitivity of ramp to ramp demand |
| |
(5)方案5:对交织区自由流速度的敏感性分析
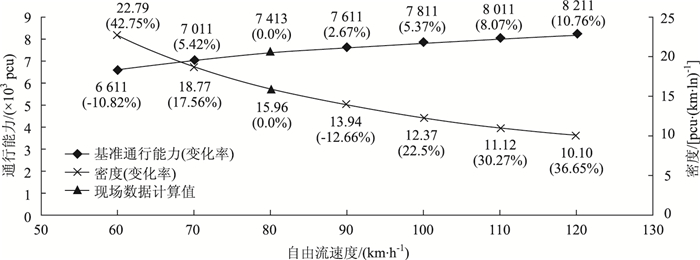
由图 9可知,自由流速度的变化对交织区通行能力影响显著,该交织区在调查时段其余参数不变的情况下,自由流速度在60~80 km/h之间时交织区通行能力和密度呈线性变化,变化率较大,交织区通行能力变化幅度为-10.82%,密度变化幅度为42.75%;自由流速度在80~120 km/h之间时交织区通行能力也呈线性变化,但变化率较小,交织区通行能力变化幅度为10.76%,密度变化幅度为-36.65%。这说明较低自由流速度对交织区交通运行影响的敏感性较大。当然,自由流速度受道路条件、交通条件、车辆动力性能和驾驶员特性等因素的影响,对自由流速度的现有判别标准即在车头时距的量化上不尽相`同,所以需进一步加强自由流速度模型的研究。
|
| 图 9 自由流速度敏感性曲线 Fig. 9 Curves of sensitivity of free flow velocity |
| |
(6)方案6:对交织区长度的敏感性分析
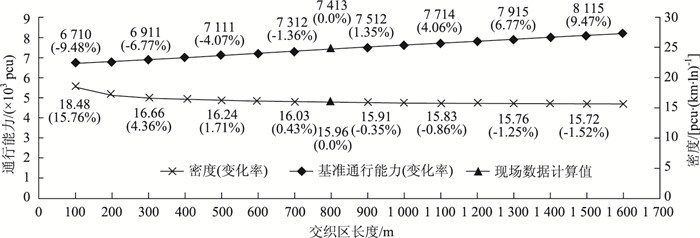
由图 10可知,交织区长度对交织区通行能力影响显著,基本呈线性变化。交织区通行能力由密度确定,交织区长度由800 m调整为100~1 600 m时,对应交织区的通行能力变化幅度为-9.48%~10.83%;交织区长度在100~300 m之间时,交织区长度对密度影响显著,变化幅度为11.4%;交织区长度在300~1 600 m之间时,交织区长度对密度影响较小,基本呈线性变化,变化幅度为6.03%。在现状交通需求水平下,交织区长度强烈影响变道密度,使得交织车辆变道空间更小,通行能力更低。当然,不同的交通需求条件下,交织区长度对交织运行敏感性的影响阈值不尽相同。
|
| 图 10 交织区长度敏感性曲线 Fig. 10 Curves of sensitivity of weaving segment length |
| |
(7)方案7:对交织区车道数的敏感性分析
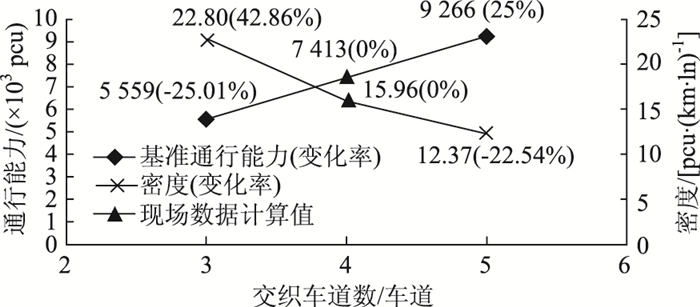
由图 11可知,该交织区在调查时段其余参数不变的情况下,交织车道数对交织区通行能力和密度影响显著,由四车道调整为三车道和五车道,交织区通行能力变化率分别为-25.01%和25.00%,密度变化率分别为42.86%和-22.54%。在此交通需求水平下,每增加1条车道就为交织和非交织车辆提供了更多的空间,同时也鼓励了附加选择性变道行为。因此,交织区通行能力就会因道路驶离能力的增强而增大,在降低整体车辆密度的同时,附加车道增加了变道行为和变道密度。但是,在多数情况下,交织区内的车道数由进出口道路车道数和交织区结构所决定。
|
| 图 11 车道数敏感性曲线 Fig. 11 Curves of sensitivity of lane number |
| |
3.3 敏感性分析结论
将以上所有参数分析中的上下限和基本案例挑选出来,绘制密度与交织区通行能力的变化图。
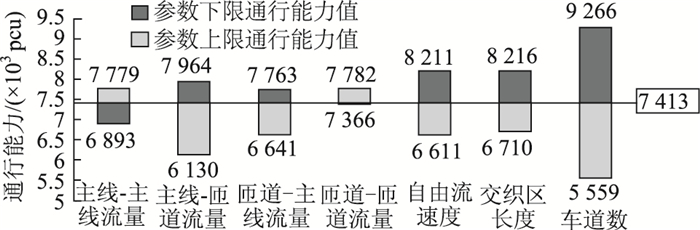
图 12说明,交织区车道数、自由流速度、匝道-主线交通流和交织区长度对交织区通行能力最具敏感性,其他3个参数引起的交织区通行能力变化较小。主线-匝道交通流和匝道-主线交通流对交织区通行能力的影响呈负相关性,即交织区的通行能力随交织流量比的增加而减小,且主线-匝道交通流至少进行一次变道行为,对交织区通行能力的影响更加显著。
|
| 图 12 基于所有参数的通行能力敏感性 Fig. 12 Capacity sensitivity based on parameters |
| |
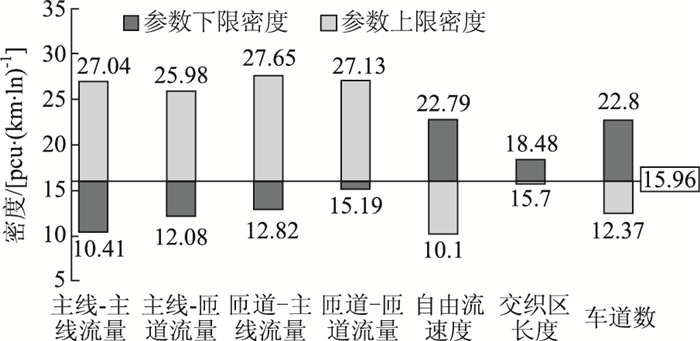
图 13说明,自由流速度、车道数和交织区长度对交织区的密度影响呈负相关性,即交织区密度随自由流速度、车道数和交织区长度的增加而减小,其中交织区长度对密度的影响最小。其他4个参数引起的密度变化呈正相关性,在现状道路条件下,对交织区密度的影响显著。
|
| 图 13 基于所有参数的密度敏感性 Fig. 13 Density sensitivity based on parameters |
| |
4 结论
(1)通过西安绕城高速公路吕小寨立交-朱宏路立交之间交织区调查数据对美国道路通行能力手册(HCM2010)交织区交织速度和非交织速度预测模型进行了修正,重新标定了相关参数,建立了适合我国道路交通条件的速度预测模型。
(2)利用Visual Basic语言开发了交织区运行分析计算工具,批量计算了交织区运行效率指标值,便于交织区影响因素对交织运行的影响分析。
(3)基于修正后的速度预测模型,借助交织区运行分析计算工具,定量分析了交织区影响因素对交织区运行状况的敏感性。结果表明,交织区车道数、自由流速度、匝道-主线交通流和长度对交织区通行能力最具敏感性;交织行为对交织区通行能力影响显著,呈负相关性。在目前道路条件下,各方向交通流量对交织区的密度影响最为显著。
(4)本文研究成果可用于匝道交通流控制,当交织区内发生交通拥堵时,可通过对出入口交通流适宜的控制率来调整交织区瓶颈内的实际车流驶入率和最优驶出率;研究结论还可优化交织区交通设计,通过增加交织区车道数、提高交织区自由流速度和增长交织区长度等措施,提高其通行能力和服务水平,缓解交通瓶颈。
(5)本文修正的交织速度模型、非交织速度模型和敏感性分析结论有力地丰富了交织区运行分析和交通优化设计方法,但由于数据有限,限制了模型精度,需进一步丰富基础数据提高模型精度、完善敏感性分析结论。
| [1] | Transportation Research Board. Highway Capacity Manual 2010[M]. Washington, D.C.: Transportation Research Board, 2010 . |
| [2] | WU N, LERSTIN K. A New Model for Level of Service of Freeway Merge, Diverge, and Weaving Segments[C]//6th International Symposium on Highway Capacity and Quality of Service. Amsterdam:Elsevier Ltd., 2011:151-162. |
| [3] | JTG B01-2014, 公路工程技术标准[S]. JTG B01-2014, Technical Standard of Highway Engineering[S]. |
| [4] | ROGER P R, EELENA S P. The Highway Capacity Manual:A Conceptual and Research History[M]. New York: Springer, 2014 . |
| [5] | 任福田, 刘小明, 荣建, 等. 道路通行能力手册[M]. 北京: 人民交通出版社, 2007 . REN Fu-tian, LIU Xiao-ming, RONG Jian, et al. Highway Capacity Manual[M]. Beijing: China Communications Press, 2007 . |
| [6] | LERTWORAWANICH P, ELEFTERIADOU L. Capacity Estimations for Type B Weaving Areas Based on Gap Acceptance[J]. Transportation Research Record , 2001, 1776 : 24-34 |
| [7] | LERTWORAWANICH P, ELEFTERIADOU L. A Methodology for Estimating Capacity at Ramp Weaves Based on Gap Acceptance and Linear Optimization[J]. Transportation Research Part B:Methodological , 2003, 37 (5) : 459-483 |
| [8] | LERTWORAWANICH P. Capacity Estimation for Weaving Areas Based on Gap Acceptance and Linear Optimization[D]. University Park, PA:The Pennsylvania State University, 2003. |
| [9] | WANG X, LUO Y, QIU T Z, et al. Capacity Estimation for Weaving Segments Using a Lane-changing Model[J]. Transportation Research Record , 2014, 2461 : 94-102 |
| [10] | WANG X, HADIUZZAMAN M, FANG J, et al. Optimal Ramp Metering Control for Weaving Segments Considering Dynamic Weaving Capacity Estimation[J]. Journal of Transportation Engineering , 2014, 140 (11) : 04014057 |
| [11] | ZHANG Y H. Capacity Modeling of Freeway Weaving Sections[D]. Blacksburg:Virginia Polytechnic Institute and State University, 2005. |
| [12] | 钟连德, 荣建, 孙小端, 等. 仿真求解快速路交织区通行能力[J]. 公路交通科技 , 2006, 23 (4) : 88-93 ZHONG Lian-de, RONG Jian, SUN Xiao-duan, et al. Capacity of Weaving Sections of Urban Expressway Obtained with Simulation Method[J]. Journal of Highway and Transportation Research and Development , 2006, 23 (4) : 88-93 |
| [13] | 雷丽, 董力耘, 宋涛, 等. 基于元胞自动机模型的高架路交织区交通流的研究[J]. 物理学报 , 2006, 55 (4) : 1711-1717 LEI Li, DONG Li-yun, SONG Tao, et al. Study on the Traffic Flow of Weaving Section in Elevated Road System with Cellular Automaton Model[J]. Acta Physica Sinica , 2006, 55 (4) : 1711-1717 |
| [14] | JIA B, LI X G, JIANG R, et al. Traffic Behavior Around the Weaving Section in Cellular Automata Model[J]. International Journal of Modern Physics C , 2010, 21 (3) : 409-422 |
| [15] | 刘立英, 李新刚, 贾斌. 基于元胞自动机模型的交织区通行能力特性分析[J]. 交通信息与安全 , 2013, 31 (3) : 28-32 LIU Li-ying, LI Xin-gang, JIA Bin. Analysis of Capacity of Weaving Section Based on Cellular Automata Model[J]. Journal of Transport Information and Safety , 2013, 31 (3) : 28-32 |
| [16] | 江金胜, 董力耘. 基于元胞自动机模型的C型交织区交通流特性[J]. 力学学报 , 2012, 44 (6) : 996-1004 JIANG Jin-Sheng, DONG Li-yun. Investigation on Traffic Flow Characteristics around a Type C weaving Section Based on Cellular Automaton Model[J]. Chinese Journal of Theoretical and Applied Mechanics , 2012, 44 (6) : 996-1004 |
| [17] | 陈小鸿, 肖海峰. 交织区交通特性的微观仿真研究[J]. 中国公路学报 , 2001, 14 (S1) : 88-91 CHEN Xiao-hong, XIAO Hai-feng. Micro-simulation Study of the Characteristics of Waving Area[J]. China Journal of Highway and Transport , 2001, 14 (S1) : 88-91 |
| [18] | 交通部公路科学研究所. 公路通行能力手册[M]. 北京: 人民交通出版社, 2002 . Research Institute of Highway of Ministry of Transport. Highway Capacity Manual[M]. Beijing: China Communications Press, 2002 . |
| [19] | 周晨静, 荣建, 冯星宇. 2010HCM交织区通行能力分析方法适用性研究[J]. 公路交通科技 , 2015, 32 (4) : 118-123 ZHOU Chen-jing, RONG Jian, FENG Xing-yu. Study of Applicability of Weaving Area Capacity Analysis Method of 2010HCM[J]. Journal of Highway and Transportation Research and Development , 2015, 32 (4) : 118-123 |
 2017, Vol. 34
2017, Vol. 34
