扩展功能
文章信息
- 王磊, 佘强, 张旭辉, 张建仁
- WANG Lei, SHE Qiang, ZHANG Xu-hui, ZHANG Jian-ren
- 人工气候下腐蚀预应力钢绞线的力学性能研究
- Study of Mechanical Property of Prestressed Strands Corroded in Artificial Climate
- 公路交通科技, 2017, 34(1): 97-102, 111
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 97-102, 111
- 10.3969/j.issn.1002-0268.2017.01.014
-
文章历史
- 收稿日期: 2014-11-01
近年来,国内外出现了一系列预应力混凝土桥梁失效的事故,如中国柳州的壶西大桥、美国的尼尔斯海峡大桥、英国的BicktonMeadons大桥和Ynys-y-Gwas大桥[1-3]。这些事故绝大部分是由预应力钢绞线腐蚀引起的。预应力钢绞线腐蚀已成为预应力混凝土桥梁主要病害之一。在不利环境下,预应力钢绞线在高应力状态下极易发生腐蚀。预应力钢绞线腐蚀过程中存在应力腐蚀和氢脆等现象,容易引起脆性失效,可能会造成预应力混凝土结构在较低腐蚀率和较小荷载的情况下失效[4-6]。因此,研究腐蚀预应力钢绞线力学性能退化规律,对掌握预应力混凝土结构性能退化和失效特征具有重要的意义。
目前,关于腐蚀预应力钢绞线力学性能退化规律的研究尚属于起步阶段。刘其伟等[7]从预应力连续梁桥拆除了不同腐蚀率的钢绞线进行力学性能研究,试验结果表明:在轻微腐蚀下,钢绞线的弹性模量及极限强度对腐蚀不敏感,屈强比和断后延伸率仍满足要求。刘文华等[8]通过海洋环境下的预应力钢绞线腐蚀试验,对腐蚀时间长达1 a及2.5 a的预应力钢绞线进行拉伸试验,发现腐蚀使其极限抗拉强度分别降低了约40%和70%。李富民等[9]通过掺氯盐混凝土构件取得腐蚀钢绞线,作静力拉伸试验,发现在0~0.58%腐蚀率水平下,钢绞线的抗拉强度降低了约9%~23%。
上述研究均未对腐蚀预应力钢绞线的本构关系模型进行探讨。曾严红等[10]由通电腐蚀获取腐蚀预应力筋,通过静力拉伸试验对腐蚀预应力筋的弹性模量、名义极限强度及极限应变等力学参数进行了分析,并以二折线本构关系模型为基础,建立了腐蚀预应力钢绞线的本构关系模型[11]。但腐蚀过程中,人工电流下已经施加的预应力是否会对钢绞线本身性能影响尚不明确。
本文通过人工气候下喷洒盐雾的腐蚀试验获取了18根腐蚀预应力钢绞线样本,然后通过腐蚀预应力钢绞线的拉伸试验来研究其力学性能,建立了腐蚀预应力钢绞线的本构关系模型,以期为腐蚀预应力混凝土结构的耐久性评估提供参考依据。
1 试验方案 1.1 腐蚀预应力钢绞线的制备本试验中所采用的预应力钢绞线为湖南英格瑞斯钢绞线厂生产的1×7-15.20-1860钢绞线,其弹性模量为1.95×105 MPa,屈服强度和极限强度分别为1 830,1 938 MPa。
通过人工气候试验箱喷洒盐雾获取18根1 000 mm长的样本,其中,S0为未腐蚀样本;D1~D10和S1~S7为人工气候下2种不同应力状态下腐蚀获得的腐蚀样本;D1~D10和S1~S7的初始应力水平分别为0.45倍和0.75倍屈服强度。
样本D1~D10和S1~S7都在如图 1所示的预应力钢绞线张拉装置上进行拉伸施加预应力。然后将装置放入人工气候箱中,通过喷洒盐雾2 h、停2 h的干湿交替进行腐蚀[12],通过控制腐蚀时间来控制试件的腐蚀率。

|
| 图 1 预应力钢绞线张拉装置 Fig. 1 Tension device for prestressed strands |
| |
腐蚀完成后,将腐蚀试件浸泡在5%(质量分数)的盐酸溶液中清洗去除浮锈,然后用石灰水中和,清水清洗干净。待试件晒干后,进行拉伸试验。
1.2 拉伸试验钢绞线的拉伸试验在LAW-600微机控制电液伺服钢绞线试验机上进行,试验装置如图 2所示。加载过程中,由测力传感器监测拉力,引伸计监测位移。按GB/T 5224-2003规定,钢绞线测量标距取最小值:500 mm。以控制位移的方式获得全程拉伸曲线,加载速度为10 mm/min,当出现第一批断丝时停止试验。

|
| 图 2 钢绞线拉伸装置 Fig. 2 Tension device for strands |
| |
试验完成后,采用截面轮廓法[13]对引申计测距范围内的3个截面的锈蚀率进行了测定(截面位置如图 2所示)。首先,将钢绞线在测定截面位置处截断,在断面上涂抹颜料;然后,将断面轮廓拓印至纸张上,并通过扫描等手段输入计算机;最后,借助计算辅助软件对拓印轮廓截面积进行测定,进而得到截面锈蚀率。选用3个测定锈蚀率的最小值,作为试件表征腐蚀率,如表 1所示。
| 试件 | S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 |
| ρ/% | 0 | 6.1 | 6.45 | 8.3 | 9.55 | 10.8 | 11.7 | 12.38 | 4.34 | 7.34 | 9.12 | 10.4 | 11.5 | 15.69 | 17.51 | 19.5 | 21.3 | 27.5 |
2 试验结果及分析 2.1 荷载-变形曲线
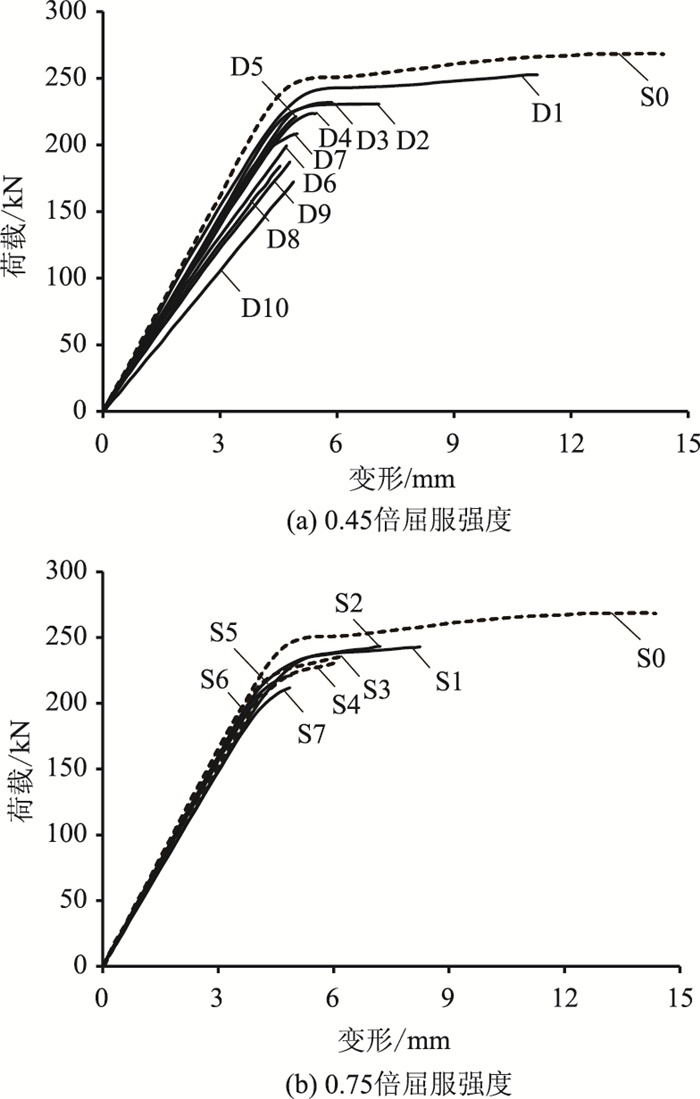
图 3为不同腐蚀率预应力钢绞线的荷载-变形曲线。由图 3可以看出,随着腐蚀率的增大,钢绞线的极限变形能力显著下降,钢绞线的极限承拉能力也逐渐降低,屈服段逐渐缩短直至消失;腐蚀率进一步增大,钢绞线在弹性状态下断裂,并且这一现象随着腐蚀率的增大而越来越显著。这是因为腐蚀减小了钢绞线的截面面积,截面的削弱效应降低了钢绞线的极限变形能力和极限承拉能力,而且坑蚀的应力集中效应使得腐蚀严重的预应力钢绞线的破坏形式从延性转变为脆性。
|
| 图 3 腐蚀钢绞线荷载-变形曲线 Fig. 3 Load-deformation curves of corroded strands |
| |
2.2 电镜扫描
拉伸试验后,在各样本钢丝断裂处截取1小段进行电镜扫描(SEM)试验,观察不同腐蚀率钢绞线钢丝断裂处断口形态及侧面的外观形态,取具有代表性的样本S0,D4及D10进行观察分析。如图 4所示,未腐蚀钢绞线S0断裂处侧面没有出现裂缝;腐蚀较轻的钢绞线D4出现了数条细小的裂缝;腐蚀严重的钢绞线D10出现了较多较宽的裂缝。

|
| 图 4 腐蚀钢绞线侧面的微观结构 Fig. 4 Microstructure of side of corroded strands |
| |
在应力状态下,钢绞线表面钝化膜容易破裂,钢绞线易发生腐蚀。此外,由于高应力的影响,钢绞线腐蚀过程中的阳极溶解使得钢绞线表面出现腐蚀裂缝,而阴极析出的氢扩展了裂缝宽度。
2.3 破坏形态拉伸试验之后,对所有断裂钢丝的断口观察发现:预应力钢绞线有着相似的破坏形态,未腐蚀钢绞线为延性断裂,断口表现出颈缩现象;随着腐蚀率的增加,腐蚀钢绞线转变为脆性断裂,断口无明显颈缩现象(见图 5)。

|
| 图 5 腐蚀钢绞线的断面形态 Fig. 5 Section morphology of corroded strands |
| |
未腐蚀钢丝所能承受的最大拉应力基本相同, 在完成较大拉伸变形后几乎在同一时间断裂,而腐蚀钢丝的腐蚀程度不同,蚀坑的深度不同使腐蚀钢丝所能承受的最大拉应力大小不一,腐蚀严重的钢丝在拉伸变形较小时就已经断裂。
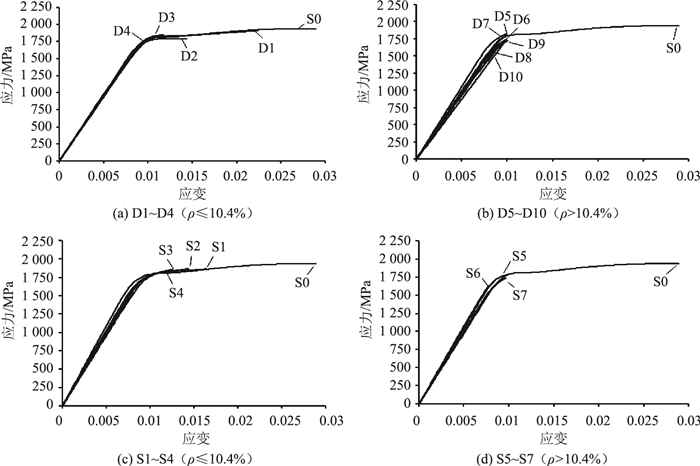
3 预应力钢绞线力学参数分析所有样本的应力-应变关系曲线如图 6所示。本文中应力为所施加的荷载与钢绞线腐蚀后残余截面面积的比值;应变为引伸计所监测到的伸长率与其测距的比值。未腐蚀试样S0的应力-应变曲线由3个阶段组成:弹性阶段、屈服阶段和硬化阶段。S0经过一段较大的变形之后,在硬化阶段断裂;腐蚀较轻的试件D1~D4和S1~S4(ρ≤10.4%)在屈服阶段或者硬化阶段出现延性破坏;腐蚀较严重的试件D5~D10和S5~S7(ρ>10.4%)都在弹性阶段脆性破坏。这表明腐蚀降低了钢绞线极限应变,会导致钢绞线脆性破坏。
|
| 图 6 应力-应变关系曲线 Fig. 6 Stress-strain curves |
| |
3.1 极限应变
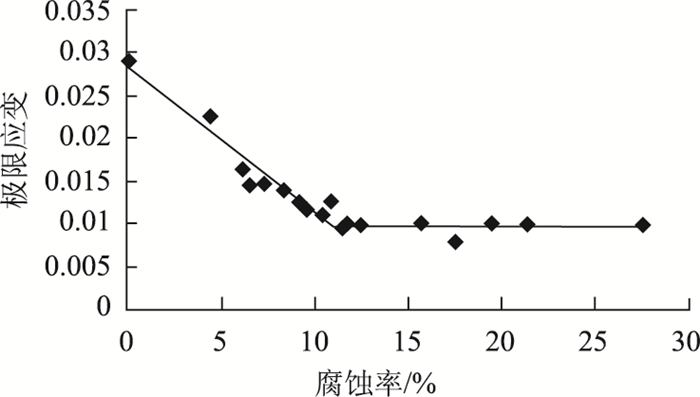
图 7统计分析了极限应变(εpc)与腐蚀率之间的关系。从图 7可以看出,当腐蚀较轻时(ρ≤10.4%),腐蚀钢绞线的极限应变随着腐蚀率的增加而线性降低;当腐蚀严重时(ρ>10.4%),钢绞线极限应变几乎不再随着腐蚀率的增大而变化。
|
| 图 7 εpc-ρ关系曲线 Fig. 7 Relationship between εpc and ρ |
| |
在相同的拉力下,蚀坑处的截面面积小,产生的应力较大,在整根钢丝还没达到其极限延伸率时,钢丝在蚀坑处已拉伸断裂,拉断时每根钢丝的延伸率较未腐蚀钢丝的极限延伸率小,故整根钢绞线的极限延伸率减小,其极限应变降低。腐蚀对拉伸试验中弹性阶段的影响较小,不同腐蚀率钢绞线在弹性阶段的极限延伸长度都相接近(见图 6,所有试件在弹性阶段的应变值都在0.01附近)。当腐蚀严重时,钢绞线都在弹性阶段脆性破坏,其延伸在弹性阶段进行,屈服阶段和硬化阶段没有进行延伸,故严重腐蚀的钢绞线极限延伸长度相近,其极限应变不再随腐蚀率的增大而变化。
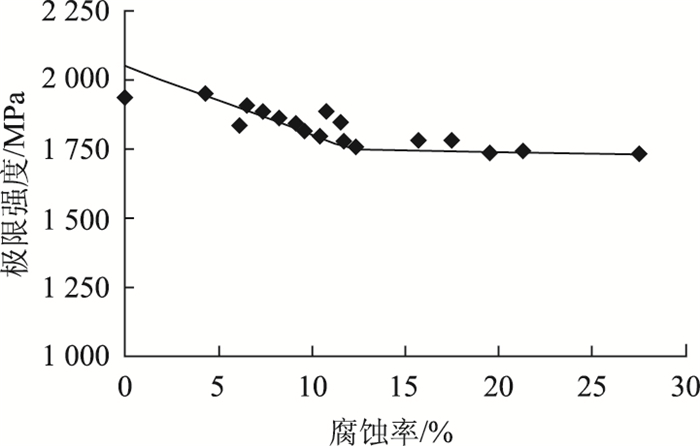
3.2 极限强度本文定义极限强度fpc为极限荷载与钢绞线腐蚀后平均截面面积的比值。经统计分析得到了如图 8所示的fpc-ρ关系。图 8表明,在腐蚀率相差不大的情况下(8%≤ρ≤12%),试件S3~S6和D3~D5的fpc都在一定的数值附近上下浮动。这可能是由于材料本身的不均匀性与坑蚀效应的随机性导致的。
|
| 图 8 fpc-ρ关系曲线 Fig. 8 Relationship between fpc and ρ |
| |
但总体来看,在腐蚀率较低的情况下,随着腐蚀率的增大,极限强度非线性减小;当腐蚀率达到临界时,极限强度不再随着腐蚀率的增大而减小,而是在某一值附近上下波动。
拉伸试验中,腐蚀钢绞线在屈服之前会出现微裂缝。屈服后,在应力作用下裂缝会迅速扩展贯穿,导致钢绞线被拉断。故腐蚀严重的钢绞线的极限强度值在未腐蚀钢绞线的屈服强度值附近波动,不会再随着腐蚀率的增大而减小。
3.3 屈服强度由预应力钢绞线的荷载-变形曲线可以看出,S0~S4和D1~D4在屈服以后断裂,而S5~S7和D5~D10在屈服之前都已断裂。经统计分析得到S0-S4和D1-D4的屈服强度(Re),如表 2所示。S1-S4和D1-D4的屈服强度较S0分别减少了3.88%, 1.3%, 2.57%, 3.98%, 1.91%, 2.96%, 5.85%和5.52%。屈服强度的最大降幅为5.85%。这表明腐蚀对钢绞线屈服强度的影响较小。
| 试件 | S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 |
| Ep/GPa | 195 | 192 | 193 | 195 | 185 | 195 | 196 | 183 | 194 | 188 | 189 | 186 | 185 | 188 | 196 | 186 | 184 | 182 |
| Re/MPa | 1 830 | 1 759 | 1 806 | 1 783 | 1 757 | - | - | - | 1 795 | 1 776 | 1 723 | 1 729 | - | - | - | - | - | - |
钢绞线的腐蚀主要是边丝腐蚀,中丝的腐蚀较小,相对边丝的屈服强度而言,中丝的屈服强度对整根钢绞线的屈服强度贡献较大。而边丝对屈服强度的影响主要体现在边丝之间相互挤压作用的咬合力。当腐蚀较轻时,边丝表面还较光滑,腐蚀对边丝之间相互挤压作用影响较小;当严重的腐蚀影响到边丝之间相互作用的咬合力时,严重的坑蚀效应会使钢绞线转变为脆性断裂。这也是S5~S7和D5~D10没有出现屈服平台的原因。
3.4 弹性模量表 2统计了本文18根不同腐蚀率钢绞线的弹性模量(Ep)。相对S0而言,腐蚀钢绞线弹性模量减小最大的为D10(182 GPa),最大降幅为6.67%, 可以认为腐蚀对弹性模量的影响不大。这是因为弹性模量主要是由材料本身的材质决定的,而腐蚀并不会引起钢绞线材质的变化,故不同腐蚀率钢绞线的弹性模量变化不大。
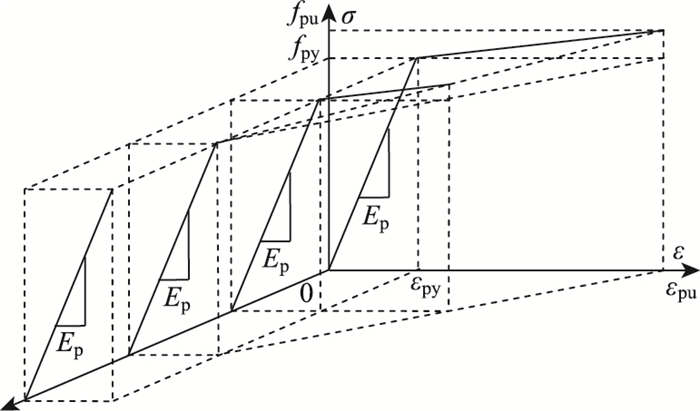
4 应力-应变关系模型目前,国内学者已经提出了多种关于钢绞线的本构关系模型[10, 14-15]。但这些模型趋于复杂,或者需要确定的参数较多,运用起来较为不便。本文通过人工气候箱对18根1×7ϕ15.2 1860级钢绞线进行了腐蚀,其锈蚀率从低到高,分布在0~27.5%之间,并通过拉伸试验得到了不同锈蚀程度下钢绞线的应力-应变关系曲线。通过对这些样本数据的分析, 可以发现未腐蚀钢绞线的应力-应变关系通常被定义为弹性-硬化双线性模型[15]。如图 6所示,腐蚀较轻的钢绞线应力-应变关系曲线随着腐蚀率的增加存在一个明显的变化。对于轻微腐蚀的钢绞线,其应力-应变关系也可以用弹性-硬化双线性模型表示,但其极限应变应比未腐蚀的小。但当腐蚀率增大到一定程度时,钢绞线的应力-应变关系退化成仅有弹性阶段的单线性模型。这些样本的本构关系数据表现出较强的规律性,反映了同类腐蚀钢绞线应力应变关系变化趋势。基于这些规律,本文提出了一个简化的腐蚀钢绞线本构关系模型,如图 9所示。
|
| 图 9 腐蚀钢绞线本构关系模型 Fig. 9 Constitutive relation model for corroded strands |
| |
本文定义引起腐蚀钢绞线应力-应变关系由双线性模型退化成单线性模型的最小锈蚀率为临界锈蚀率。从前面的试验数据分析可知,本试验中临界锈蚀率取值约为10.4%。该本构关系模型可进一步描述为:轻微腐蚀钢绞线的极限应变与极限强度随腐蚀率的增大而线性降低,当腐蚀率达到临界值时,极限应变与极限强度不再随腐蚀率的增大而变化;
腐蚀钢绞线的弹性模量及屈服强度对腐蚀率不敏感。腐蚀钢绞线的本构关系可以表示为:
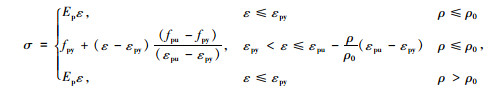
|
(1) |
式中,σ为腐蚀钢绞线应力;ε为腐蚀钢绞线应变;εpy,εpu,fpy,fpu,Ep分别为未腐蚀钢绞线的屈服应变、极限应变、屈服强度、极限强度和弹性模量。
文中给出的本构关系表达式是一个通用公式。鉴于不同厂家、不同规格和批次的钢绞线,弹性模量、屈服强度和极限强度等参数间可能会存在一定的偏差,为此,本文用相应符号代表这些参数,以增强模型的适用性。实际应用中,钢绞线的初始弹性模量、屈服强度、极限强度等力学参数需以实际值为基准,其腐蚀后的本构模型需将相应参数代入式(1)中即可。
5 结论(1)应力作用下,钢绞线的腐蚀十分复杂。在截面积损失的同时,其表面还伴随着微裂纹的形成。腐蚀率较低时,微裂缝细小且数量较少;腐蚀率严重时,微裂缝数量增加,宽度变宽。
(2)在腐蚀率较低的情况下,钢绞线极限应变可近似地视为随腐蚀率线性降低,极限强度轻微下降;当腐蚀率达到临界值时,极限应变与极限强度不再随腐蚀率的增大而降低;腐蚀对钢绞线弹性模量与屈服强度影响非常小。
(3)钢绞线的应力-应变曲线一般有弹性、屈服和硬化3阶段组成,随着腐蚀的发展,钢绞线的屈服阶段和硬化阶段会明显缩短,当钢绞线的腐蚀超过临界腐蚀率时,其应力-应变曲线只有弹性阶段,屈服阶段和硬化阶段都会消失。
(4)本文提出的腐蚀钢绞线本构关系模型以腐蚀率作为控制参数,运用较为方便。但该本构关系可能受到腐蚀环境、样本数量等的影响。不同腐蚀环境,大样本试验,尤其是实际结构中腐蚀钢绞线样本试验数据验证,将增强该模型的准确性和精度,这些工作有待进一步补充完善。
| [1] | 朱尔玉, 刘椿, 何立, 等. 预应力混凝土桥梁腐蚀后的受力性能分析[J]. 中国安全科学学报 , 2006, 16 (2) : 136-140 ZHU Er-yu, LIU Chun, HE Li, et al. Stress Performance Analysis on Corroded Pre-stressed Concrete Beam[J]. China Safety Science Journal , 2006, 16 (2) : 136-140 |
| [2] | DARMAWAN M S, STEWART M G. Effect of Pitting Corrosion on Capacity of Prestressing Wires[J]. Magazine of Concrete Research , 2007, 59 (2) : 131-139 |
| [3] | Concrete Society. Durable Post-Tensioned Concrete Bridges, Technical Report No.47[R]. Crowthorne, UK:Concrete Society, 2002. |
| [4] | PODOLNY W, J r. Corrosion of Prestressing Steels and Its Mitigation[J]. PCI Journal , 1992, 37 (5) : 34-55 |
| [5] | SALAS R M, SCHOKKER A J, WEST J S, et al. Corrosion Risk of Bonded, Post-Tensioned Concrete Elements[J]. PCI Journal , 2008, 53 (1) : 89-107 |
| [6] | 余芳, 贾金青, 宋玉普. 钢绞线腐蚀后的部分预应力混凝土梁抗弯疲劳性能试验研究[J]. 建筑结构 , 2012, 42 (1) : 97-100 YU Fang, JIA Jin-qing, SONG Yu-pu. Experimental Research on Fatigue Behavior of Prestressed Concrete Beams with Corroded Steel Strands[J]. Building Structure , 2012, 42 (1) : 97-100 |
| [7] | 刘其伟, 张鹏飞, 赵佳军. PC连续梁桥孔道压浆调查及钢绞线力学性能研究[J]. 施工技术 , 2007, 36 (2) : 63-66 LIU Qi-wei, ZHANG Peng-fei, ZHAO Jia-jun. Duct Grouting Investigation and Research on Mechanical Properties of Steel Strand in PC Continuous Bridges[J]. Construction Technology , 2007, 36 (2) : 63-66 |
| [8] | 刘文华, 李文春, 马全声. 高强钢丝钢绞线在海洋环境中的腐蚀试验[J]. 海威姆预应力技术 , 2001 (2) : 34-38 LIU Wen-hua, LI Wen-chun, MA Quan-sheng. Corrosion Test of High-strength Steel Wire Strand in Marine Environment[J]. HVM Prestressing Technology , 2001 (2) : 34-38 |
| [9] | 李富民, 袁迎曙, 杜健民, 等. 氯盐腐蚀钢绞线的受拉性能退化特征[J]. 东南大学学报:自然科学版 , 2009, 39 (2) : 340-344 LI Fu-min, YUAN Ying-shu, DU Jian-min, et al. Deterioration of Tensile Behavior of Steel Strands Corroded by Chloride[J]. Journal of Southeast University:Natural Science Edition , 2009, 39 (2) : 340-344 |
| [10] | 曾严红, 顾祥林, 张伟平, 等. 锈蚀预应力筋力学性能研究[J]. 建筑材料学报 , 2010, 13 (2) : 169-174 ZENG Yan-hong, GU Xiang-lin, ZHANG Wei-ping, et al. Study on Mechanical Properties of Corroded Prestressed Tendons[J]. Journal of Building Materials , 2010, 13 (2) : 169-174 |
| [11] | DARMAWAN M S, STEWART M G. Spatial Time-dependent Reliability Analysis of Corroding Pretensioned Prestressed Concrete Bridge Girders[J]. Structural Safety , 2007, 29 (1) : 16-31 |
| [12] | BARTON S C, VERMAAS G W. Accelerated Corrosion and Embrittlement of High-strength Bridge Wire[J]. Journal of Materials in Civil Engineering , 2000, 12 (1) : 33-38 |
| [13] | HIGGINS C, FARROW Ⅲ W C. Tests of Reinforced Concrete Beams with Corrosion-Damaged Stirrups[J]. ACI Structural Journal , 2006, 103 (1) : 133-141 |
| [14] | 楼铁炯, 郭乙木, 王振林. 双筋工形预应力混凝土梁截面的非线性分析[J]. 土木工程学报 , 2004, 37 (7) : 47-50 LOU Tie-jiong, GUO Yi-mu, WANG Zhen-lin. Nonlinear Analysis on Section with I-shape of Double-reinforcement Prestressed Concrete beam[J]. China Civil Engineering Journal , 2004, 37 (7) : 47-50 |
| [15] | ZONA A, RAGNI L, A DALL'AST A. Finite Element Formulation for Geometric and Material Nonlinear Analysis of Beams Prestressed with External Slipping Tendons[J]. Finite Elements in Analysis and Design , 2008, 44 (15) : 910-919 |
 2017, Vol. 34
2017, Vol. 34
