扩展功能
文章信息
- 田增顺, 刘钱, 郭佳, 李法雄, 李茜
- TIAN Zeng-shun, LIU Qian, GUO Jia, LI Fa-xiong, LI Qian
- 预制小箱梁桥拓宽施工工艺研究
- Study on Widening Technology of Small Precast Box Girder Bridge
- 公路交通科技, 2017, 34(1): 83-88
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 83-88
- 10.3969/j.issn.1002-0268.2017.01.012
-
文章历史
- 收稿日期: 2015-07-09
2. 温州市高速公路投资有限公司, 浙江 温州 325003;
3. 交通运输部公路科学研究院, 北京, 100088
2. Wenzhou Expressway Investment Co., Ltd., Wenzhou Zhejiang 325003, China;
3. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
针对桥梁拓宽的施工工艺,国内外学者已经开展大量的试验和理论研究工作[1-3]。交通荷载及其振动是影响混凝土湿接缝强度发展和最终结构整体性的重要因素,潜在的损坏类型包括:混凝土早期开裂、湿接缝的抗弯剪强度降低等[4-5]。减小交通荷载下混凝土湿接缝两侧挠度差是保障工程质量的最切实可行的方法,具体措施有:(1)实行交通管制;(2)设置临时支承;(3)设置临时剪力架;(4)混凝土湿接缝分时分段浇注;(5)施加钢骨体系辅助措施。
京津塘高速扩建工程中,对20 m跨径的简支T梁桥接缝采用5-10-5分段浇注方式,接缝周期为4天,并没有对分段方式与接缝周期间的关系进行详细阐述。本文所研究的改扩建工程中拟定了4种交通组织方案和4种分时分段浇注方案,建立考虑混凝土弹性模量发展的有限元模型。根据混凝土弹性模量发展规律,求解4种交通组织方案和4种分时分段浇注方案下湿接缝混凝土两侧挠度差随时间变化规律,判定交通组织方案和分时分段浇注方案的合理性及有效性。
1 通车下交通组织及分时分段方案为保证通车条件下预制小箱梁桥拼宽施工过程中接缝混凝土浇注质量,减小湿接缝两侧最大挠度差,目前最简捷有效的方式是实行交通管制。本文所研究的改扩建工程中拟定了4种交通管制方案,如表 1所示,通过封闭与拼宽接缝毗邻的车道和限制重车通行来实现。
| 序号 | 方案1 | 方案2 | 方案3 | 方案4 |
| 描述 | 老桥所有两车道均对交通开放并承受标准车道荷载,老桥应急车道作为施工作业面。 | 拼宽接缝毗邻的车道承受车辆荷载最大值为3.24 t (SUV),其余车道对承受标准车道荷载,老桥应急车道作为施工作业面。 | 封闭与拼宽接缝毗邻的车道与应急车道一起作为施工作业面,其余车道对交通开放并承受标准车道荷载。 | 封闭与拼宽接缝毗邻的车道与应急车道一起作为施工作业面,其余车道承受车辆荷载最大值为3.24 t (SUV)。 |
| 示意图 | 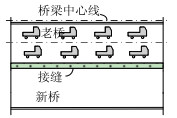 | 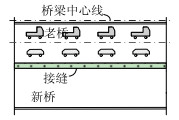 | 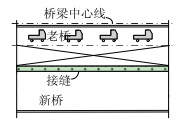 | 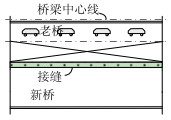 |
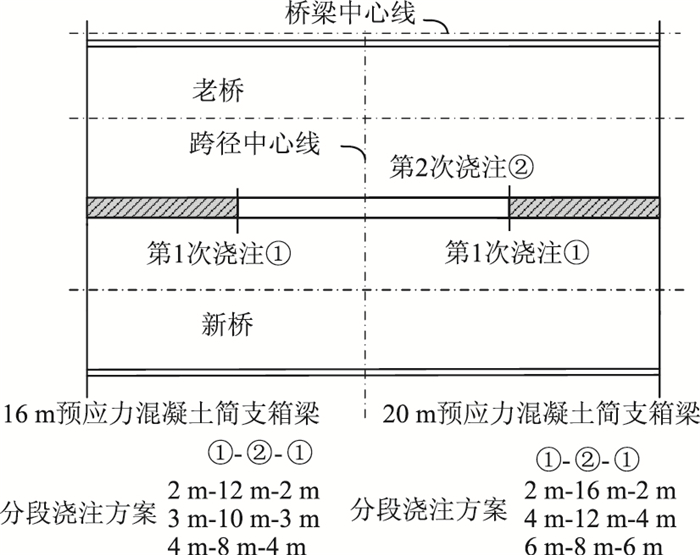
分时分段浇注措施中的分段浇注指的是混凝土湿接缝的浇注从梁端向跨中逐段推进,而每两段之间浇注的间隔时间即为分时。分时分段浇注的原理是在两端支座附近一定长度内,可以认为该段混凝土接缝在承受少量交通荷载的情况下进行浇注,当第一段接缝混凝土达到一定强度后,该段混凝土接缝可发挥连续剪力架的作用,将老桥桥面板的部分交通荷载传递到新桥桥面板上,从而减小混凝土接缝的挠度差,为下一段湿接缝的浇注奠定基础。合理的分段布局应该是使整个浇注过程中各个阶段最大挠度差达到最小,即, 使各个阶段下挠度差尽量接近。初步确定的拼宽接缝分段布局及各阶段浇注长度如图 1所示。
|
| 图 1 分段浇注方案示意图 Fig. 1 Schematic diagram of segmented pouring scheme |
| |
2 受力性能分析 2.1 工程概况
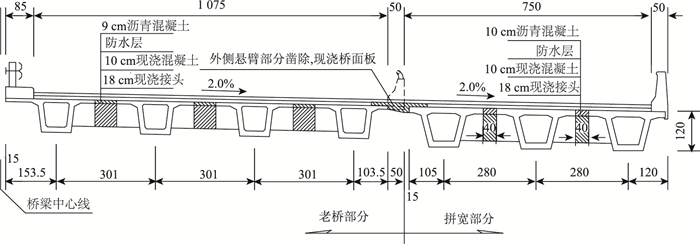
某高架桥全长8.7 km,上部结构为20 m预应力混凝土简支小箱梁,桥面连续。桥梁拓宽设计遵守“老桥旧标准,新桥新标准”原则,新旧小箱梁桥拼宽标准横截面如图 2所示。
|
| 图 2 小箱梁桥拼宽标准横断面(单位:cm) Fig. 2 Standard cross-section of small box girder bridge widening (unit:cm) |
| |
预制小箱梁桥拼宽设计方案为:(1)采用“上部结构连接、下部结构分离”的拼接方式,新旧箱梁拼接处翼板采用“刚性连接”,下部结构盖梁不连接;(2)新桥侧由3片20 m小箱梁装配而成,单片小箱梁高度1.2 m,相邻小箱梁横向中心距2.8 m;(3)新旧箱梁连接仅通过翼板,不设置端横隔板;(4)切除老桥护栏及边梁50 cm翼板混凝土,保留内部钢筋,新桥边梁翼板预留钢筋;(5)拼接缝两侧箱梁横向中心距2.735 m,湿接缝宽度为65 cm,厚度由新桥侧28 cm渐变为老桥侧的20 cm。
2.2 有限元模型建立 2.2.1 单元选取Abaqus模型中沥青和混凝土铺装层以及橡胶支座的单元类型均为C3D8R,采用结构化网格划分技术;预制小箱梁结构相对复杂,采用最为灵活的自由网格划分技术,先在变截面处分割为几个区域之后再赋予C3D4单元属性。新老桥实体模型与之类似,湿接缝混凝土采用C3D8R单元类型。
2.2.2 材料模型考虑到行车荷载下桥梁挠度及应变均较小,结构各部分未发生屈服,实体模型中所有材料均采用线弹性本构模型来定义,各部件材料参数如表 2所示。
| 名称 | 混凝土强度 等级 | 弹性模量 E/MPa | 泊松比v | 重度/ (kN·m-3) |
| 主梁 橡胶支座 沥青铺装 混凝土铺装 湿接缝 | C50 - - C40 C50 | 3.45×104 843.75 1.5×104 3.25×104 - | 0.2 0.4 0.2 0.2 0.3 | 25 - 24 25 25 |
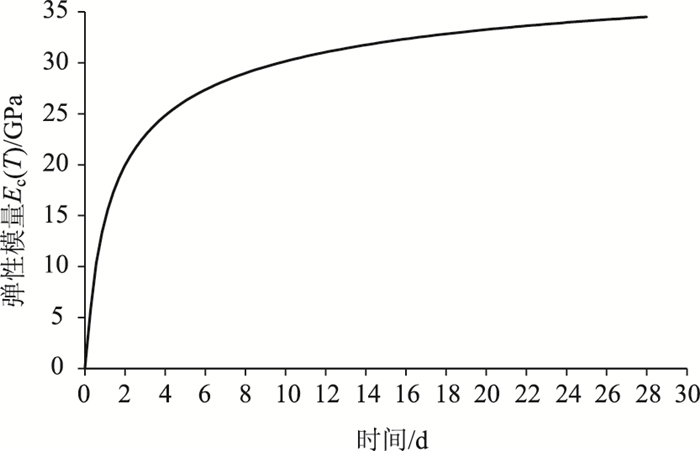
其中,湿接缝混凝土弹性模量曲线如图 3所示,按照规范CEB-FIP MC90取值,表达式为:
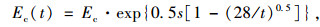
|
(1) |
|
| 图 3 混凝土弹性模量发展曲线 Fig. 3 Elastic modulus development curve of concrete |
| |
式中,Ec为龄期28 d时的混凝土弹性模量;s为水泥类型系数。快硬高强水泥值为0.2,翼板水泥值为0.25,缓凝水泥值为0.38;t为混凝土浇注后天数。
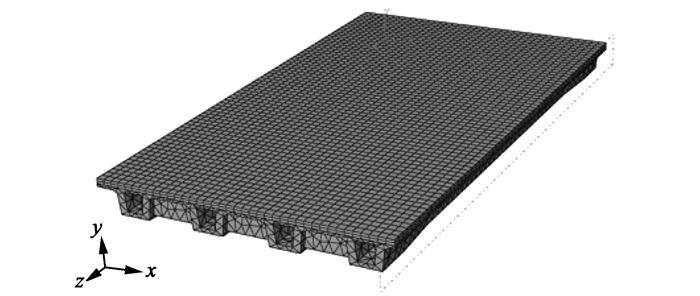
2.2.3 有限元模型图 4为拓宽前的老桥模型示意图,预制小箱梁老桥主要由4大部件组成:沥青铺装层、混凝土铺装层、预制小箱梁和橡胶支座,本节将详细介绍这4者之间的关系及其在模型中的实现。
|
| 图 4 预制小箱梁老桥模型 Fig. 4 Prefabricated old small box girder bridge model |
| |
沥青与混凝土铺装层以及支座的建模是先在Sketch模块中绘制截面形状,然后对其Extrusion (拉伸)得到。主梁的等截面区段直接通过拉伸建模,变截面区段需要先对两端等截面区段的位置进行调整,然后选取等截面区段侧面封闭的截面图形进行Loft (放样)操作。沥青铺装层与混凝土铺装层之间、混凝土铺装层与主梁之间、主梁与支座之间均选取约束类型为Tie (绑定约束),把主、从两个面牢固地黏结在一起,分析过程中不再分开。
图 5为拓宽后的新老桥模型示意图。此模型与老桥模型相比,建模方法及约束类型均一致,不必再行赘述。

|
| 图 5 预制小箱梁老桥+新桥模型 Fig. 5 Prefabricated old and new small box girder bridge model |
| |
2.3 接缝混凝土两侧挠度差分析
使用Midas Civil软件建立老桥模型,通过其特有的移动荷载追踪器功能确定4种交通管制方案下车辆荷载的最不利加载位置。对5轴总重55 t重车轴载及车队纵横向排列的规定参照1989年公路桥涵通用设计规范[6-8],对限重车道小车的轴载定义为满座时总重3.2 t的某SUV:前后轴距2.825 m,满载时前后轴轴重均定义为16.2 kN。
根据计算所得最不利加载位置布载,计算4种方案下老桥拼宽侧跨中挠度值如表 3所示。
| 交通管制 | 方案1 | 方案2 | 方案3 | 方案4 |
| 挠度/mm | 4.983 | 2.564 | 1.822 | 0.316 |
| 注:表中挠度代表老桥拼宽侧跨中下挠值即拼宽侧最大下挠值。 | ||||
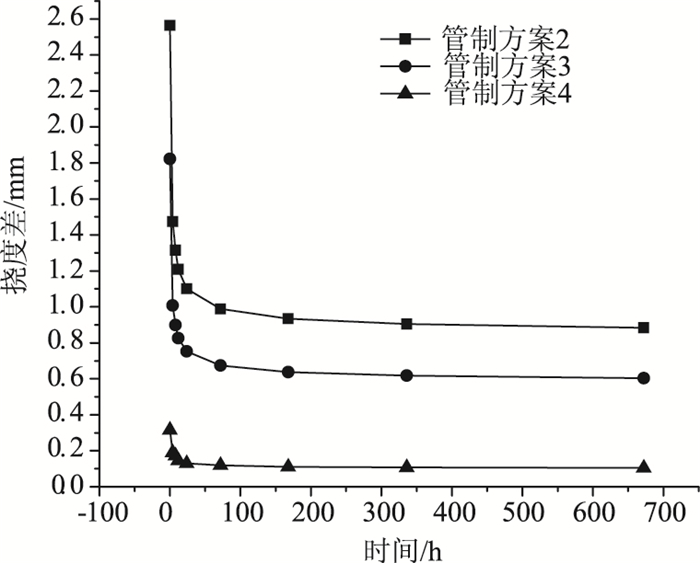
在桥梁拓宽工程中,湿接缝浇注和养护初期,没有交通荷载传递到新的桥面板上,仅老桥桥面承受交通荷载弯曲下挠;随着养护时间增长,湿接缝混凝土形成一定的强度,新桥的桥面板将随老桥一起变形[9]。因此,随着养护中混凝土湿接缝强度逐渐增大,横向传递荷载能力变强,湿接缝两侧混凝土挠度差逐渐减小。通过改变混凝土弹性模量模拟后3种交通管制方案在不同养护时间下湿接缝混凝土两侧挠度差,其变化趋势如图 6所示。
|
| 图 6 不同养护时间下湿接缝两侧挠度差 Fig. 6 Deflection differences between both sides of wet joint under different curing time |
| |
混凝土早期强度发展较快,前3天挠度差下降明显,3天之后变化缓慢。3种交通管制方案下混凝土浇注4,8,24,72 h后通车挠度差降低的比例如表 4所示。
| 时间/mm | 方案2/% | 方案3/% | 方案4/% |
| 4 | 42.5 | 44.7 | 39.6 |
| 8 | 51.3 | 50.7 | 45.6 |
| 24 | 57.2 | 58.7 | 58.9 |
| 72 | 61.5 | 63.0 | 62.3 |
交通荷载作用下混凝土湿接缝两侧挠度差在跨中位置取最大值,从跨中到支座湿接缝挠度和挠度差渐变为零。混凝土接缝的施工浇注可以分为若干阶段,但考虑到工期和进度,通常分为2阶段和3阶段进行浇注,每两个阶段间的间隔时间称为接缝周期。在本模型中接缝周期设定为4,24,72 h,分段方案分为2-16-2,4-12-4,5-10-5,6-8-6这4种。
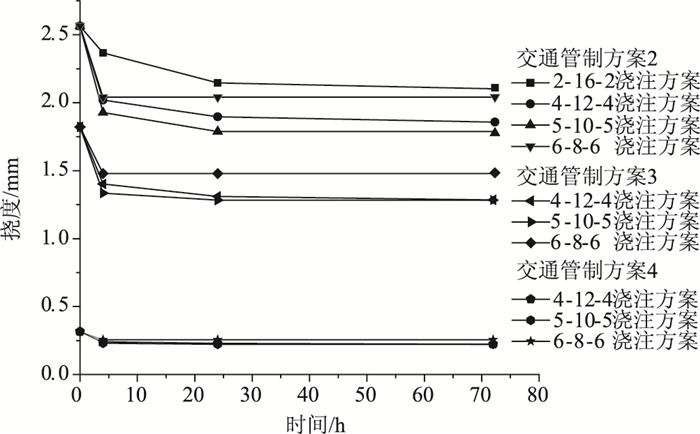
首先计算交通管制方案2下2-16-2,4-12-4,5-10-5,6-8-6这4种接缝浇注方案下湿接缝挠度差,发现2-16-2方案下第1阶段浇注时挠度差太小,第2阶段浇注时挠度差太大,控制挠度差过大,因此在以后的备选的浇注方案中舍去此方案。而4-12-4浇注方案中第2阶段大于第1阶段挠度差,6-8-6浇注方案第1阶段大于第2阶段挠度差,为寻找最优方案,简单运用二分法取5-10-5方案,继续计算交通管制方案3、4。3种交通管制方案所对应的分时分段浇注方案下湿接缝挠度差如图 7所示。
|
| 图 7 3种交通管制方案所对应的分时分段浇注方案下湿接缝挠度差 Fig. 7 Deflection differences of wet joint under different time-sharing segmented pouring schemes corresponding to 3 traffic schemes |
| |
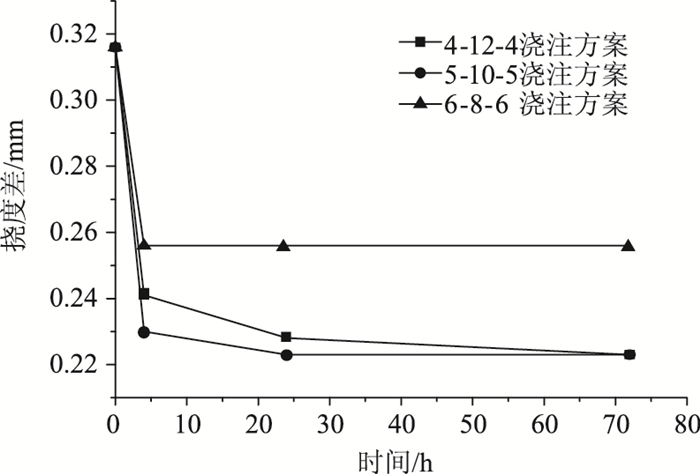
结果表明,接缝周期4 h到1 d时接缝混凝土强度发展最快,挠度差下降明显,接缝周期为4 h的5-10-5方案下控制挠度差减小25%,接缝周期1 d时控制挠度差减小31%,1 d到3 d控制挠度差基本趋于稳定。交通管制方案4对应3种不同分时分段浇注方案下控制挠度差变化曲线如图 8所示。
|
| 图 8 交通管制方案4在不同分时分段浇注方案下湿接缝控制挠度差 Fig. 8 Controlled deflection differences of wet joint of different time-sharing segmented pouring schemes under traffic control scheme 4 |
| |
结果显示,第4种交通组织方案下采取接缝周期为1 d的5-10-5分段方案比整垮浇注控制挠度差减小30%,与不采取任何措施降低95.5%;接缝周期为3 d时,4-12-4与5-10-5分段方案效果相同,同整垮浇注相比控制挠度差减小30%,不同的是4-12-4分段方案控制挠度差在第2阶段,而5-10-5分段方案控制挠度差在第1阶段。若接缝周期大于3 d,4-12-4分段方案控制挠度差将会减小,相比5-10-5分段方案渐显优势。
3 桥梁拓宽横向分布系数分析对于拓宽桥梁的荷载横向分布特性,常规的理论计算方法并不适用,可以采用数值分析技术来解决。应用等效梁格建立桥梁上部结构有限元模型,利用主梁的挠度或内力来分析荷载横向分布特征[10-11]。其中主梁挠度ω、弯矩M或剪力Q满足:
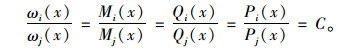
|
(2) |
根据梁的挠曲理论,主梁弯矩Mx、剪力Qx计算公式为:
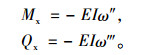
|
(3) |
若取荷载为单位正弦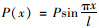
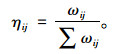
|
(4) |
王浩[12]等取不同的湿接缝厚度研究连接刚度大小对加宽桥梁荷载横向分布,得出:随湿接缝厚度增加(即刚度增大),各梁的横向分布系数随之减小,这说明新旧梁连接刚度增大可有效提高桥梁的承载性能。
采用合理的分时分段浇注方案及其他措施,有效控制接缝两侧挠度差,提升混凝土接缝浇注质量,即提高横向连接刚度,减小各梁的横向分布系数,提高桥梁的整体工作性能。
4 结论本文介绍通车条件下预制小箱梁桥拼宽施工过程中通过实行交通管制、分时分段浇注措施,对湿接缝两侧挠度差减小效果的分析,得出以下结论:
(1)实行交通管制可以有效减小跨中挠度,方案4与方案1相比较挠度值减小93.6%。
(2)混凝土早期强度发展较快,挠度差迅速下降,前3天挠度差下降最大达到58.9%,72 h之后变化趋于缓慢。
(3)20 m跨简支梁桥分两阶段浇注时,接缝时间在3天以内时,5-10-5分段方案效果较好,接缝时间大于72 h时则优选4-12-4分段方案。
(4)若选择接缝周期为1 d,计算结果显示5-10-5分段方案为最优,在此推荐的浇注方案是交通管制方案4+5-10-5分段方案+接缝周期1 d,挠度差比不采取任何措施降低95.5%。
(5)通过提升混凝土浇注质量,增大新旧桥横向连接刚度,可有效减小各梁的横向分布系数,提高桥梁的整体工作性能。
| [1] | 曲向进.沈大高速公路改扩建工程技术方案研究[D].大连:大连理工大学, 2003. QU Xiang-jin. Study on Technology of Shenyang-Dalian Expressway Expansion Project[D]. Dalian:Dalian University of Technology, 2003. http://www.oalib.com/references/18405040 |
| [2] | 马春生, 宋神友. 广佛高速公路湖洲大桥主桥新旧结构连接设计[J]. 公路 , 2003 (8) : 63-66 MA Chun-sheng, SONG Shen-you. Design of Connection between New Beam and Old One of Huzhou Bridge on Guangfo Expressway[J]. Journal of Highway , 2003 (8) : 63-66 |
| [3] | 桂炎德. 高速公路拓宽设计方法初探[J]. 公路 , 2004 (7) : 59-64 GUI Yan-de. Method of Highway Widening Design[J]. Highway , 2004 (7) : 59-64 |
| [4] | 杜进生. 高速公路桥梁拓宽中几个问题的讨论[J]. 公路 , 2008 (7) : 169-174 DU Jin-sheng. Discussion on Several Issues in Expressway Bridge Widening[J]. Highway , 2008 (7) : 169-174 |
| [5] | 惠小荣.交通荷载对拓宽桥梁接缝的影响研究[D].北京:北京交通大学, 2008. HUI Xiao-rong. Study on Concrete Stitch of Widening Bridge under Traffic Load[D]. Beijing:Beijing Jiaotong University, 2008. |
| [6] | JTG D64-2004, 公路钢筋混凝土及预应力混凝土桥梁设计规范[S]. JTG D64-2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [7] | JTG D60-2004, 公路桥涵设计通用规范[S]. JTG D60-2004, General Code for Design of Highway Bridges and Culverts[S]. |
| [8] | JTG 021-1989, 公路桥涵设计通用规范[S]. JTG 021-1989, General Code for Design of Highway Bridges and Culverts[S]. |
| [9] | 方益红. 高速公路桥梁拼宽改造关键问题分析[J]. 福建建筑 , 2009 (9) : 129-131 FANG Yi-hong. Analysis of Key Problems in Bridge Widening and Reconstructions in Expressway[J]. Fujian Architecture & Construction , 2009 (9) : 129-131 |
| [10] | 陈兴中.预制装配式小箱梁桥横向分布计算方法的研究分析[D].西安:长安大学, 2007:57. CHEN Xing-zhong. Study on Transverse Load Distribution Calculation Method of Small Prefabricated Box Girder Bridge[D]. Xi'an:Chang'an University, 2007:57. http://www.cnki.com.cn/Article/CJFDTOTAL-LNJT201201011.htm |
| [11] | 李国豪, 石洞. 公路桥梁荷载横向分布计算[M]. 北京: 人民交通出版社, 1987 . LI Guo-hao, SHI Dong. Calculation on Transverse Load Distribution of Highway Bridge[M]. Beijing: China Communications Press, 1987 . |
| [12] | 王浩, 朱若溪, 张肇红. 连接刚度对加宽桥梁荷载横向分布的影响分析[J]. 公路 , 2013 (7) : 143-146 WANG Hao, ZHU Ruo-xi, ZHANG Zhao-hong. Analysis of Influence of Connection Stiffness on Transverse Load Distribution of Widened Bridge[J]. Highway , 2013 (7) : 143-146 |
 2017, Vol. 34
2017, Vol. 34
