扩展功能
文章信息
- 张驰, 王世伟, 黄星, 熊丽
- ZHANG Chi, WANG Shi-wei, HUANG Xing, XIONG Li
- 基于多因素的道路线形拟合方法综合评价
- Study on Comprehensive Evaluation of Road Alignment Fitting Method Based on Multi-factor
- 公路交通科技, 2017, 34(1): 54-60
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 54-60
- 10.3969/j.issn.1002-0268.2017.01.008
-
文章历史
- 收稿日期: 2016-01-28
2. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710075
2. CCCC First Highway Consultants Co., Ltd., Xi'an Shaanxi 710075, China
近年来,道路工程快速发展,截至2015年末,全国公路总里程446.39万km,比上年末增加10.77万km。新建道路工程的增长趋于稳定,而道路的改扩建工程则呈现逐年增长的趋势。一些道路年代久远,线形资料已经丢失,所以这些道路改扩建设计就必须对该路段进行线形拟合,来获取遗失的道路线形资料。在道路线形拟合中,平面线形拟合设计是纵断面拟合设计的基础,在完成平面拟合设计后,基于平面拟合的结果完成纵断面拟合。并且平面线形比纵断面线形更加复杂,工作量更高,所以道路线形拟合的关键在于平面线形的拟合。
有关道路线形拟合方法的研究一直是道路改扩建领域中的热点,当下平面拟合方法的种类众多,平面拟合的方法可分为两类:一类是从数学角度进行道路线形拟合,主要有插值函数、样条函数法、二次多项式法、三弯矩法等;另一类是从应用角度研究线形元素的选取与搭配以及CAD技术的开发。国外学者对道路线形拟合的研究主要集中在自动化提取和识别道路线形。2000年Drakopoulos and Örnek等[1]提出了利用GIS地图完成对道路线形的计算和识别。2007年Easa, Haibin Dong[2]提出了利用卫星地图来构建道路平面线形,从地图中提取道路线形要素。2012年Zhixia Li, Madhav V[3]提出了以Curve Finder为基础的线形识别方法,并将道路分割成线形单元,利用线形单元特性进行拟合。2015年Chengbo Ai[4]提出了基于GPS数据的道路线形识别和线形要素测设方法。国内学者对道路线形拟合研究的起步较晚,同济大学的杨轸博士[5-6]提出了基于GPS的道路线形拟合方法,将最小二乘法和GPS测量数据应用于道路线形拟合。武汉理工大学的王红副教授[7]提出了一种基于MATLAB和CAD平台的道路线性拟合方法,通过MATLAB的曲线拟合工具箱和编程程序,实现对道路线形的拟合。武汉理工大学的张航副教授[8]对三次样条曲线法拟合道路平面线形进行了研究,并编写了三次样条曲线法拟合道路线形的软件。东南大学的张志伟等[9]利用航测数据,提出了基于LIDAR数据的道路平面线形拟合方法。
现有的道路线形拟合方法繁多,在进行道路线形拟合时,存在线形拟合方法选择的问题。而线形拟合方法的选择将直接影响着道路平面线形拟合质量和效率,因此有必要对现有的道路线形拟合方法进行评价,基于不同评价因素的优劣得到道路线形拟合方法。本文提出了基于层次分析法的多因素评价体系,探究对3种常用拟合方法的拟合精度、稳定性、难易性,并对其进行综合评价,得到了3种方法在不同因素下的优缺点,从而对道路改扩建工程的线形拟合方法选择起到一定的指导作用。
1 道路线形拟合方法本文选取了3种常用的道路线形拟合方法:基于GPS数据的最小二乘法、三次样条曲线法和基于MATLAB的半自动拟合法。利用上述3种方法对同一实测数据进行了拟合,利用本文提出的多因素评价体系对拟合结果进行了评价。
1.1 最小二乘法2003年,同济大学杨轸博士提出了基于GPS数据的最小二乘法线形拟合方法。该方法将目前最为常用的最小二乘法和GPS数据结合起来,从而提高最小二乘法的精度和准确度[5]。基于GPS数据的最小二乘法对道路线形的直线和圆曲线进行拟合时,通过平均圆心和删除直线部分异常点进行直线和圆曲线部分的拟合,最后通过解算,从而拟合出缓和曲线线形,将拟合的精度达到最优。
1.2 样条曲线法样条曲线法是比较原始的一种线形拟合方法,它是在得到道路线形数据后,用样条函数对目标道路线形进行拟合,本次介绍的是三次样条曲线法。当分段函数S(kx)为三次函数时,在{a,b}区间上具有连续的二阶导数,称为三次样条曲线[8]。由于三次样条曲线的二阶导连续,而需要拟合的线形中,直线部分的一阶导数为零,圆曲线的二阶导数为零,缓和曲线的二阶导数连续,三次样条曲线和其吻合较好,故可以利用三次样条曲线对目标道路进行拟合。
1.3 基于MATLAB的半自动拟合法本文还选取了基于MATLAB的半自动拟合方法,以武汉理工大学王红副教授提出的基于MATLAB和CAD平台的道路线形拟合方法为基础[7],利用MATLAB平台,实现对道路线形的半自动化拟合。圆曲线部分拟合以Kasa算法[10]为基础,编写圆曲线拟合的M文件,实现圆曲线拟合的半自动化拟合。直线部分则用线性回归方式,利用MATLAB拟合工具箱实现半自动化拟合。得到直线和圆曲线的参数后,通过CAD平台的图解得到缓和曲线部分道路线形参数,即可完成对目标道路的线形拟合工作。
2 多因素评价体系评价因素本文的研究目的是对目前常用的道路线性拟合方法进行评价,得到较优的道路线形拟合方法。为此本文提出了基于层次分析法的多因素评价体系,道路线形拟合方法的评价因素众多,其中只有小部分是对道路线形拟合方法选取时有影响。在因素选取时,主要考虑拟合算法的稳定性、精度、难易性,经济性等因素。由于拟合算法的经济问题在道路线形拟合选取时,影响程度较小,大部分是人工花费,故和难易性呈线性关系,因此本文不对拟合算法的经济性进行考虑。最后选取道路线形拟合方法的精度、稳定性、难易性作为综合评价体系的评价因素。
本文的原始数据为西部某山区二级公路的道路中线实测数据,该路段长60.949 km,有6 688个实测数据点。利用上述3种方法对这一路段进行拟合,并以此为基础,对比3种方法的拟合结果,可以得到3种拟合结果的精度、稳定性、难易性的分析结果。此处需要说明的是,线形拟合的结果并不等同于道路线形,线形拟合的拟合结果只能代表测量的中线线形,并不是实际的中线线形,但是3种方法采用的原始数据相同,则拟合结果中都包含实测数据和实际线形的误差,因此本文在评价时忽略道路中线实测数据和实际道路线形的误差,假设道路中线的实测数据即为道路的实际线形。
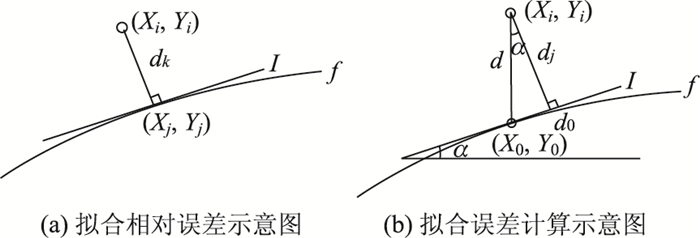
2.1 拟合精度为研究3种拟合方法的拟合精度,本文提出了拟合相对误差的概念,相对误差dk计算公式如下所示:

|
(1) |
式中,Xi, Yi为实测数据点的横坐标和纵坐标,Yi, Yj为实测数据点i对应于拟合结果点j的横坐标和纵坐标。拟合相对误差计算图如图 1所示。
|
| 图 1 拟合相对误差 Fig. 1 Fitted relative error |
| |
dk为实测数据点到拟合函数的最短距离,则直线部分的计算图如图 1(a)所示,曲线部分的计算示意图如图 1(b)所示。曲线部分的拟合相对误差dk=d0+dj,由于曲线部分d0相对于dj非常小,因此本文的曲线部分拟合相对误差dk采用近似值dj来表征。其中:
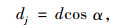
|
(2) |
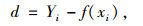
|
(3) |
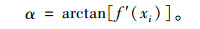
|
(4) |
最后用拟合中线误差估值的形式近似代替均方差作为平面线形的拟合精度指标。则第i段的拟合精度mi可由第i段的拟合相对误差dik求得,公式如下:
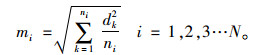
|
(5) |
旧路平面线形拟合全线拟合精度M公式如下[11]:
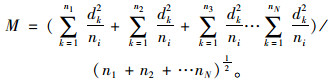
|
(6) |
利用上述公式,对各段的拟合精度mi和全线拟合精度M进行了计算,现得到3种方法的拟合精度分布如图 2~图 5所示。
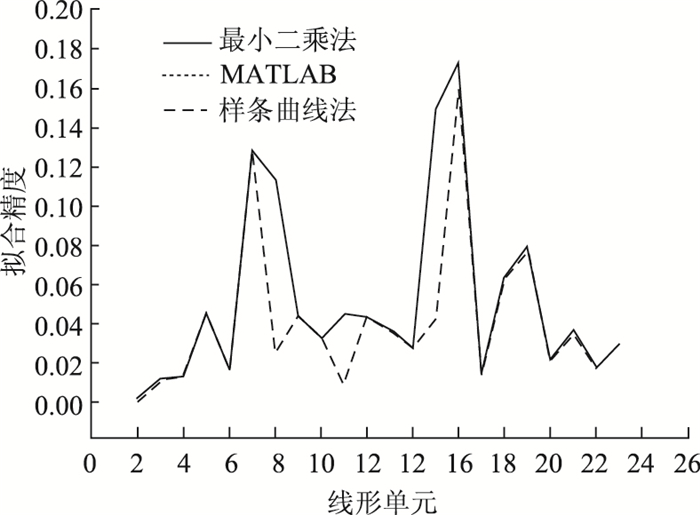
|
| 图 2 直线部分拟合精度 Fig. 2 Fitting accuracy of straight line |
| |
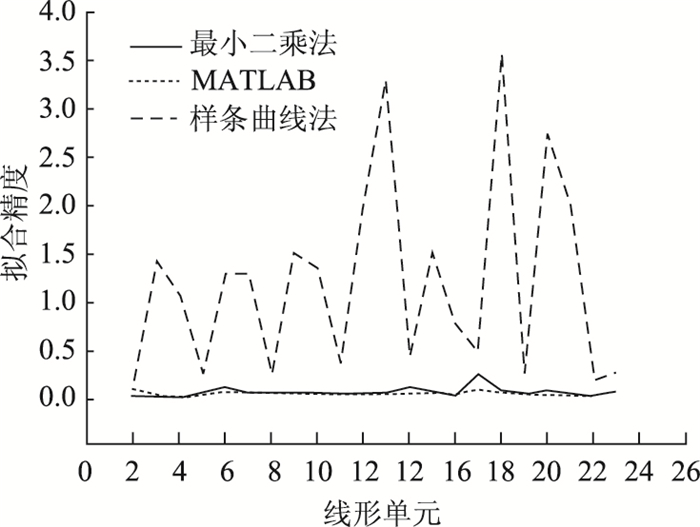
|
| 图 3 圆曲线部分拟合精度对比 Fig. 3 Fitting accuracy of circular curve |
| |
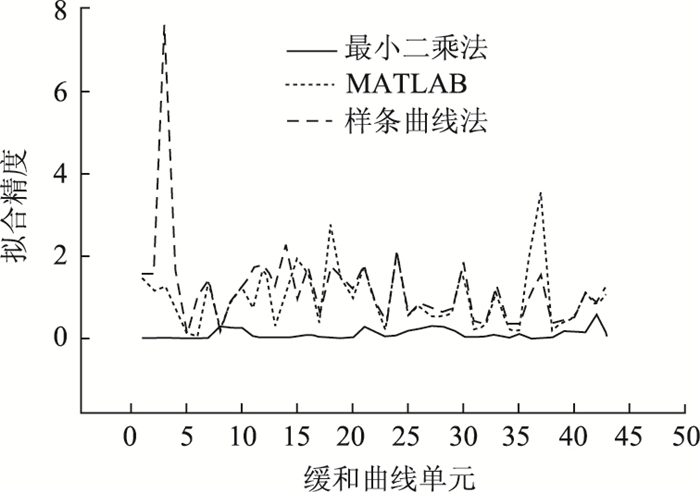
|
| 图 4 缓和曲线部分拟合精度对比 Fig. 4 Fitting accuracy of transition curve |
| |
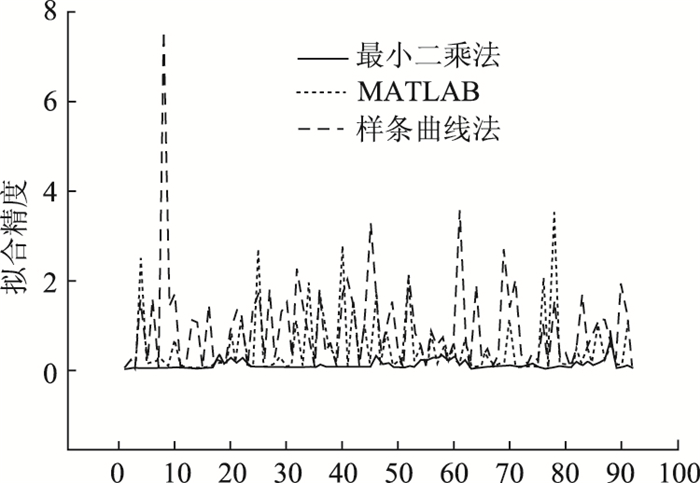
|
| 图 5 全线拟合精度对比 Fig. 5 Comparison of fitting accuracy of all curves |
| |
由拟合精度分布图可知,三次样条曲线法和MATLAB拟合工具箱都是采用线性回归的方式,确定直线部分的系数,因此两种方法得到直线部分的结果相同,基于MATLAB的半自动拟合法和三次样条曲线法的精度在直线段稍稍优于最小二乘法。圆曲线部分的拟合,最小二乘法和MATLAB拟合法的精度明显优于样条曲线法,而最小二乘法和MATLAB拟合法相比,MATLAB拟合方法在圆曲线拟合精度上要稍优于最小二乘法。在缓和曲线段拟合中,最小二乘法拟合的精度最高,MATLAB和样条曲线两种方法在缓和曲线拟合中,拟合精度较低。
同时计算得到3种方法的全线拟合精度M、直线段的拟合精度MZ、圆曲线段的拟合精度My、缓和曲线段的拟合精度Mh,计算结果如表 1所示。
| 拟合精度 | 直线单元 | 圆曲线单元 | 缓和曲线单元 | 全线精度 |
| 最小二乘法 | 0.070 | 0.095 | 0.196 | 0.122 |
| MATLAB | 0.064 | 0.057 | 0.791 | 0.354 |
| 样条曲线法 | 0.064 | 1.157 | 1.329 | 1.157 |
由计算结果可知,直线段部分,基于GPS数据的最小二乘法拟合精度为基于MATLAB的半自动拟合法和样条曲线法的91.79%,精度相差在毫米级别。圆曲线部分,最小二乘法拟合精度是基于MATLAB法的60.35%,样条曲线法则仅为MATLAB法的4.94%。缓和曲线部分,MATLAB法的拟合精度是最小二乘法的24.78%,样条曲线法的拟合精度是最小二乘法的14.75%。在全线精度对比中,最小二乘法精度最优,基于MATLAB的半自动拟合次之,最后是三次样条曲线法。基于MATLAB的半自动拟合法精度是最小二乘法的34.46%,三次样条曲线法精度是基于GPS数据的最小二乘法的10.54%。就分部精度来看,基于GPS数据的最小二乘法在缓和曲线拟合中,明显优于其他两种方法。在圆曲线拟合中,基于MATLAB的半自动化拟合法要优于其他两种方法。在直线拟合中,3种方法的误差相差不大。
2.2 稳定性稳定性是指拟合算法的误差波动大小,如果拟合算法的误差波动过大,则其在进行算法拟合时会严重影响其准确度和可靠性。当进行某一路段拟合时,其有可能总体精度很高,但是某部分的拟合误差很大,从而影响其拟合结果的评价。此处用稳定性系数p来表征拟合算法的稳定性,其计算公式如下:
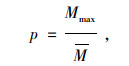
|
(7) |
式中,p为稳定性系数; Mmax为拟合误差的最大值; M为拟合相对误差的平均值。
稳定性系数p的值越大,则该道路线形拟合方法的稳定性越差。为了使稳定性系数能更好地反映拟合算法的稳定性,减小某一次偶然误差对稳定性的影响,故本次拟合误差最大值Mmax采用前5位拟合误差极值的平均值。3种方法的直线部分、圆曲线部分、缓和曲线部分的拟合误差对比图如图 6所示。
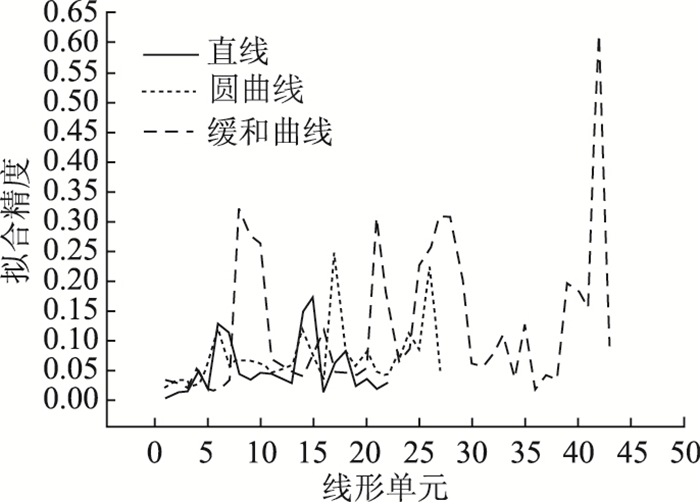
|
| 图 6 最小二乘法线形单元拟合精度对比 Fig. 6 Comparison of fitting precisions of alignment units from least square method |
| |
由图 6~图 8可知,最小二乘法拟合的误差主要是缓和曲线部分拟合产生的,直线和缓和曲线误差相差不大,同时并没有出现很大的峰值。基于MATLAB的半自动拟合法的误差主要集中在缓和曲线,并且缓和曲线的误差出现了很大的波动。而样条曲线法的误差较明显,主要集中在圆曲线和缓和曲线,且在缓和曲线部分有一个较大的误差峰值。
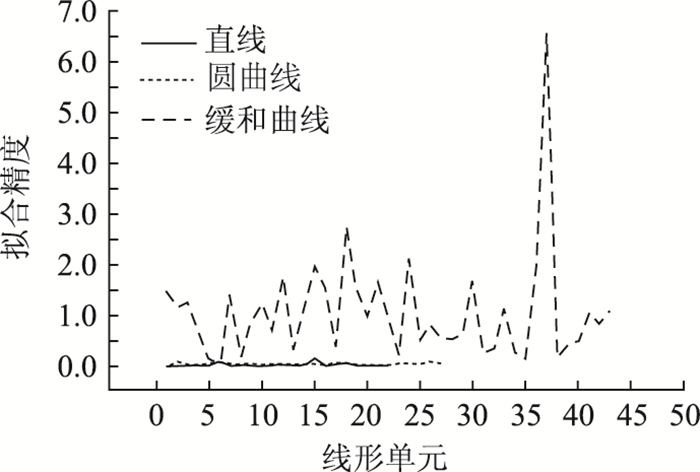
|
| 图 7 基于MATLAB的半自动拟合法线形单元拟合精度对比 Fig. 7 Comparison of fitting precisions of alignment units from MATLAB based semi automatic fitting method |
| |

|
| 图 8 样条曲线法线形单元拟合精度对比 Fig. 8 Comparison of fitting precisions of alignment units from spline curve method |
| |
基于GPS数据的最小二乘法的前5位最大拟合误差平均值M1max=0.426, 基于MATLAB的半自动拟合法的前5位最大拟合误差平均值M2max=1.174,三次样条曲线法的前5位最大拟合误差平均值M3max=5.246,则计算出稳定性p1=3.492,p2=3.316,p3=4.534。可以看出,在算法的稳定性上,基于MATLAB半自动化拟合和基于GPS数据的最小二乘法稳定度相差不大,基于MATLAB的半自动化拟合要略优于最小二乘法,三次样条曲线的稳定性最差。
2.3 难易性本文还对3种方法道路线形拟合方法的难易程度进行了评价。道路线形拟合方法的难易程度不仅影响着软件操作性和完成时间,同时也在一定程度上影响着使用者造成的误差和算法的经济问题。本文以对拟合方法的学习时间和处理数据的时间长短来表征方法的难易程度。根据3种方法对西部山区实测数据的拟合时间以及学习时间,得到3种方法的难易程度对比图如图 9所示。

|
| 图 9 难易程度对比 Fig. 9 Comparison of difficulty levels |
| |
在训练时间方面,基于MATLAB的半自动化拟合法是基于GPS数据的最小二乘法的1.25倍,是三次样条曲线法的2.5倍。处理数据的时间方面,最小二乘法是MATLAB法的4倍,是三次样条曲线的2.40倍。故基于本文提出的评价指标,在简便性方面,基于GPS数据的最小二乘法要难于其他两种方法,三次样条曲线法在3种方法里训练时间和处理数据时间最短,所以三次样条曲线法为最简便的道路线形拟合方法。基于GPS数据的最小二乘法难易性是三次样条曲线法的47.2%,基于MATLAB半自动拟合法是样条曲线法的91.67%。
3 多因素评价体系评价结果本文提出了基于多因素的道路线形拟合评价体系,利用层次分析法确定评价因素的权重,并对3种道路线形拟合方法进行了综合评价。
(1)确定评价体系的判断矩阵P[12]。首先定义其权重集A={a1, a2, a3},其中a1为拟合精度,a2为稳定性权重因子,a3为难易性权重因子。本文采用问卷调查的形式,对10位长期进行道路线形拟合的专家学者进行了问卷调查,将3个性能因素的重要性进行了两两对比,得到了3种拟合方法的性能因素判断矩阵。重要性判别表[13]和判断矩阵如表 2和表 3所示。
根据专家的评分结果可以看出,精度和稳定性的重要性基本相同,而精度要比难易性略重要,由此判断矩阵可以计算出3个性能因素的权重。
(2)判断矩阵的具体形式如下:
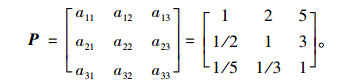
|
对权重向量W做归一化或正规化处理,即W=(0.582, 0.309,0.109)。
(4)一致性检验,以上特征向量是否就是合理的权重分配,还需对判断矩阵进行一致性检验。计算得CR=0.003 6 < 0.1,表明矩阵P具有良好的一致性。因此W可作为其权重系数,则可得权重系数W=(0.582,0.309,0.109)。
(5)拟合方法评价
根据第二部分对道路线形拟合因素的分析结果,结合每个因素的权重,对道路线形拟合方法进行综合分析。进行道路线形拟合方法综合评价时,将每个评价因素的指标进行归一化和逆指标处理,完成对3种拟合方法的综合评价。基于GPS数据的最小二乘法、基于MATLAB的半自动拟合法、三次样条线法的评价结果如表 4所示。
| 拟合方法 | 拟合精度 | 稳定性 | 难易性 | 总评分 | |||||
| 评分 | 权重 | 评分 | 权重 | 评分 | 权重 | ||||
| 最小二乘法 | 1 | 0.582 | 0.949 | 0.309 | 0.472 | 0.109 | 0.927 | ||
| MATLAB | 0.345 | 0.582 | 1 | 0.309 | 0.515 | 0.109 | 0.566 | ||
| 三次样条曲线法 | 0.105 | 0.582 | 0.731 | 0.309 | 1 | 0.109 | 0.396 | ||
最后将评价结果进行对比,最小二乘法评分A1=0.927,基于MATLAB的半自动拟合法的评分A2=0.566,三次样条曲线法的评分A3=0.396,则可以得出,基于GPS数据的最小二乘法是本文提出的多因素评价体系中最优的道路线形拟合方法,基于MATLAB的半自动拟合法是最小二乘法的61.06%,三次样条曲线的评分为最小二乘法的42.72%。
根据本文的综合评价体系,可以得出,基于GPS数据的最小二乘法相较于其他方法,仍有很大的优势,主要体现在缓和曲线部分的拟合精度和稳定性方面。基于MATLAB的半自动拟合法是基于MATLAB拟合工具箱和KASA算法进行拟合,其在自动化拟合上有很大的优势和应用前景。三次样条曲线法是3种方法中拟合最简便的,而且原理最简单,利用三次样条曲线法能够很快地获取道路的大致线形。
4 结论利用本文提出的基于层次分析法的多因素评价体系对3种道路线形拟合方法进行评价,可得到相关结论如下:
(1)本文分别对3种拟合方法进行了精度、稳定性、难易性的研究。精度方面,最小二乘法精度最高;稳定性方面,基于MATLAB的半自动拟合法稍稍优于其他方法;难易性方面,样条曲线法最简便,最小二乘法最难。最后利用层次分析法得到3种方法的综合评分,最小二乘法评分最高,基于MATLAB的半自动拟合法的评分为最小二乘法的61.06%,三次样条曲线法是最小二乘法的42.72%。
(2)应用多因素评价体系对道路线形拟合方法进行综合评价,对道路线形拟合方法起到了一定的指导作用。当对精度要求高,且线形拟合数据量较大,可以选用基于GPS数据的最小二乘法;基于MATLAB的半自动拟合法,其直线和圆曲线的精度较优,在农村不设缓和曲线的四级公路中可以应用,同时其在自动化拟合方面会有很大的应用前景。三次样条曲线法的精度相较于两种方法较低,但是其比较简便,当我们需要了解大致线形,对精度要求较低可以采用。
(3)在多因素评价方法确定权重时,采用的层次分析法带有一定的主观性。但3个评价因素之间的权重是动态的,因此在实际的改扩建工程中,可以以工程实际为导向,确定评价因素之间的重要程度,从而选择出最符合该工程的道路线形拟合方法。
(4)现有的道路线形拟合方法众多,由于笔者精力有限,只对其中较常见的3种方法进行了评价,因此得到的结果并不全面。同时,旧路平面线形拟合方法的其他因素评价以及相关技术有待进一步研究。
| [1] | DRAKOPOULOS A, ÖRNEK E. Use of Vehicle-collected Data to Calculate Existing Roadway Geometry[J]. Journal of Transportation Engineering , 2000, 126 (2) : 154-160 |
| [2] | EASA S M, DONG H, LI J. Use of Satellite Imagery for Establishing Road Horizontal Alignments[J]. Journal of Surveying Engineering , 2007, 133 (1) : 29-35 |
| [3] | LI Zhi-xia, CHITTURI M, BILL A. Automated Identification and Extraction of Horizontal Curve Information from Geographic Information System Roadway Maps[J]. Transportation Research Record , 2012, 2291 : 80-91 |
| [4] | AI Cheng-bo, TSAI Yi-chang. Automatic Horizontal Curve Identification and Measurement Method Using GPS Data[J]. Journal of Transportation Engineering , 2015, 141 (2) : 1-9 |
| [5] | 杨轸, 方守恩, 高国武. 基于GPS的道路线形恢复技术的研究[J]. 同济大学学报:自然科学版 , 2003, 31 (5) : 567-571 YANG Zhen, FANG Shou-en, GAO Guo-wu. Alignment Parameters Recovery Technique Based on GPS[J]. Journal of Tongji University:Natural Science Edition , 2003, 31 (5) : 567-571 |
| [6] | 杨轸, 朱照宏. 车载GPS用于恢复道路线形的研究[J]. 山东交通科技 , 2003, 30 (4) : 67-69 YANG Zhen, ZHU Zhao-hong. Study on Road Alignment Recovery by On-board GPS[J]. Shandong Jiaotong Keji , 2003, 30 (4) : 67-69 |
| [7] | DING Jia-jun, WANG Hong. Existing Highway Horizontal Alignment Recovery Technique Based on MATLAB and CAD Platform[C]//International Conference on Electric Technology and Civil Engineering. Lushan:IEEE, 2011:4977-4980. |
| [8] | 张航, 黄云, 龚良甫. 基于三次样条函数拟合公路平面线形方法研究[J]. 武汉理工大学学报:交通科学与工程版 , 2007, 31 (5) : 925-927 ZHANG Hang, HUANG Yun, GONG Liang-pu. Study on Fitting Highway Alignment Based on the Cubic Spline Function[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition , 2007, 31 (5) : 925-927 |
| [9] | 张志伟, 刘志刚, 黄晓明, 等. 基于LIDAR数据的道路平面线形拟合方法研究[J]. 公路交通科技 , 2009, 26 (12) : 17-22 ZHANG Zhi-wei, LIU Zhi-gang, HUANG Xiao-ming, et al. Research on Fitting Method of Road Horizontal Alignment Based on LIDAR Data[J]. Journal of Highway and Transportation Research and Development , 2009, 26 (12) : 17-22 |
| [10] | KASA I. A Circle Fitting Procedure and Its Error Analysis[J]. IEEE Transactions on Instrumentation and Measurement , 1976, IM-25 (1) : 8-14 |
| [11] | 刘苏, 王文强, 查旭东, 等. 基于法线偏差的旧路平面线形拟合精度评估方法[J]. 中国公路学报 , 2007, 20 (5) : 36-40 LIU Su, WANG Wen-qiang, ZHA Xu-dong, et al. Estimate Method for Accuracy of Fitting Plane Linear in Old Highway Based on Normal Error[J]. China Journal of Highway and Transport , 2007, 20 (5) : 36-40 |
| [12] | 常建娥, 蒋太立. 层次分析法确定权重的研究[J]. 武汉理工大学学报 , 2007, 29 (1) : 153-156 CHANG Jian-e, JIANG Tai-li. Research on the Weight of Coefficient through Analytic Hierarchy Process[J]. Journal of Wuhan University of Technology , 2007, 29 (1) : 153-156 |
| [13] | 王云.城市交通隧道安全评价体系及方法研究[D].成都:西南交通大学, 2003. WANG Yun. Study on Safety Evaluation System and Method of Urban Traffic Tunnel[D].Chengdu:Southwest Jiaotong University, 2003. |
 2017, Vol. 34
2017, Vol. 34
