扩展功能
文章信息
- 魏道江, 潘洪科, 李慧民, 张勇
- WEI Dao-jiang, PAN Hong-ke, LI Hui-min, ZHANG Yong
- 基于前景-证据理论的深基坑施工风险控制方案决策
- Decision-making of Risk Control Scheme in Construction of Deep Excavation Based on Prospect and Evidence Theory
- 公路交通科技, 2017, 34(1): 46-53
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 46-53
- 10.3969/j.issn.1002-0268.2017.01.007
-
文章历史
- 收稿日期: 2015-12-17
2. 西安建筑科技大学 土木工程学院, 陕西 西安 710055
2. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an Shaanxi 710055, China
近年来,随着我国城市地下空间开发利用的迅猛发展,越来越多的深基坑工程不得不在城市建筑密集区域施工,由于这些基坑大多邻近既有建筑、城市道路、市政管网等,基坑施工过程中的风险控制问题尤为重要[1-3]。目前,工程界主要通过风险识别、风险分析、风险评价、风险预警等手段将基坑施工风险控制在可接受范围内[4]。然而,由于各种不确定性因素的影响,基坑施工中难免出现风险评价值超过风险预警值的情形,即工程处于危机状态。此时,如何根据具体施工情境,选择合理的风险控制方案以化解工程危机是值得研究的课题。
从以往学者们的研究成果来看,危机状态下的方案决策有两个显著特点:其一,决策的时间短,短时间内决策意味着决策所需要的信息通常是不完全的;其二,决策者的主观意愿(期望)对决策结果有着非常大的影响。出于以上两点考虑,学者们提出了多种可行的决策方法,比较有代表性的文献有:蒋风光基于证据推理理论,研究了备选方案的指标值为区间灰数时的快速应急决策方法[5];吴兵运用证据理论和逼近理想解排序法建立了内河失控船应急决策模型[6];樊治平提出一种基于前景理论的应急响应风险决策方法[7];刘明对应急不完全信息环境下的混合多属性协同决策方法进行了研究[8];郑晶从案例匹配和方案生成两个角度出发,提出一种基于证据推理的考虑总体优势度的应急决策方法[9]。尽管对应急决策的研究目前已成为学者们研究的热点,但在深基坑施工风险控制领域却并未见有相关报道。有鉴于此,本文提出一种将前景理论与证据理论相结合的深基坑施工风险控制方案决策方法,以应对施工过程中风险评价值超过风险预警值时的风险控制问题。
1 深基坑施工风险控制方案决策指标体系对深基坑施工风险控制方案进行决策就是对多层次、多指标构成的复杂指标体系进行递归分析[10]。因此,决策指标体系的建立是深基坑施工风险控制方案决策的前提。本文根据基坑施工风险控制的特点,并考虑决策者的主观意愿,根据科学性、完备性、独立性、可测性以及层次性的原则,建立了由目标层、准则层、因素层构成的深基坑施工风险控制方案决策指标体系,如图 1所示。
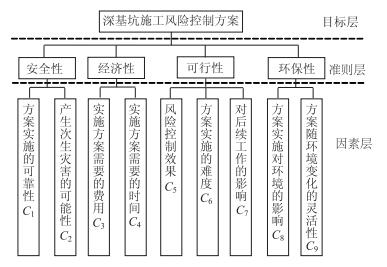
|
| 图 1 深基坑施工风险控制方案决策指标体系 Fig. 1 Decision-making index system for risk controlscheme in construction of deep excavation |
| |
2 深基坑施工风险控制方案决策模型 2.1 指标形式转化及规范化处理
由深基坑施工风险控制方案决策指标体系可知,有些决策指标为定量指标,可以用精确数或区间数表示,如实施方案所需要的费用、时间等; 有些指标为定性指标,只能用语义语言表示,如方案实施的难易程度、对后续工作的影响等。因此,深基坑施工风险控制方案决策属于混合型多属性决策问题。为了描述不同类型指标值的不确定性并对其进行合成,本文首先将混合型指标初始值统一转化为区间数的形式,具体方法如下:
假设用指标值xij表示对第i个方案第j个决策指标所作的评价值,用Ej表示决策者对第j个决策指标的期望值,不失一般性,假设xij≥0,Ej≥0,其中,i=1, 2, …, m,m为方案总数;j=1, 2, …, n,n为决策指标总数,则:
(1)当xij,Ej为精确数时,令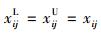
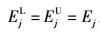
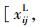
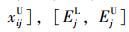
(2)当xij,Ej为区间数时,二者的区间数形式为其本身,分别为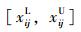
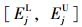
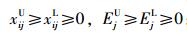
(3)当xij,Ej为语言变量时,假设该语言变量取值于一种预先定义好的语言变量集S,且有S={Sf|f=0, 1, …,(T/2)-1, T/2,(T/2)+1, …, T},其中,Sf表示S中第f+1个语义语言,T为偶数,S中共包含T+1个元素。例如,当T=6时,S={S0, S1, S2, S3, S4, S5, S6},依次对应着“非常低,低,较低,中,较高,高,非常高”7个状态。且S满足有序性,即当f>g时,Sf>Sg,表示状态Sf优于状态Sg。则将xij,Ej转化为区间数形式分别为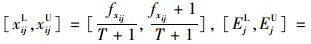
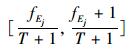
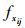
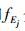
另外,在混合型多属性决策问题中,指标的属性又可分为效益型和成本型两种类型,分别记作CB和CC,效益型的属性值越大越好,成本型的属性值越小越好。因此,为了消除不同物理量纲对决策结果的影响,需要进一步对转化后的xij及Ej进行规范化处理,方法如下:
令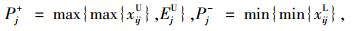
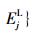
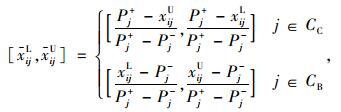
|
(1) |
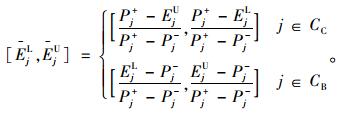
|
(2) |
数据规范化处理后,得到方案决策矩阵X=[xij]m×n,以及期望向量E={E1, E2, …, Ej, …, En}。
2.2 确定前景决策矩阵根据前景理论的原理,决策者将通过计算各方案的指标评价值与参照点之间的距离,得到各指标的损益值,并以此为依据建立前景决策矩阵V=[V(xij)]m×n,具体步骤为:
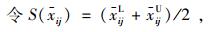
|
(3) |
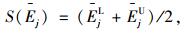
|
(4) |
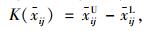
|
(5) |
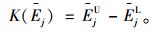
|
(6) |
依据文献[11],当S(xij)≠S(Ej)时,若S(xij)>S(Ej),则xij>Ej;若S(xij) < S(Ej),则xij < Ej。当S(xij)=S(Ej)时,若K(xij) < K(Ej),则xij>Ej;若K(xij)=K(Ej),则xij=Ej;若K(xij)>K(Ej),则xij < Ej。
计算各备选方案的指标评价值xij与期望指标值Ej之间的距离:
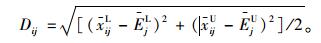
|
(7) |
根据xij与Ej的大小关系,得到各指标相对于参照点的损益值F(xij):
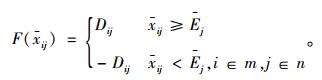
|
(8) |
这里,当xij≥Ej时,称F(xij)为指标值xij相对于期望值Ej获得的收益;当xij < Ej时,称F(xij)为指标值xij相对于期望值Ej产生的损失。考虑到决策者对待收益和损失的风险态度并不相同,因此,建立前景决策矩阵>V=[V(xij)]m×n,其中,V(xij)表示第i个方案的第j个指标前景值,其计算公式为:
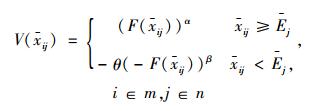
|
(9) |
式中,参数α和β表示前景值V(xij)的凸凹程度,即决策者在面对收益时是凹函数,表现出风险厌恶,在面对损失时是凸函数,表现出风险偏好,且有0 < α < 1,0 < β < 1;参数θ表示决策者对损失的规避程度,θ>1,θ值越大,表示决策者在面对损失时的风险规避程度越大。根据Birnbaum[12]、He Xuedong[13]等学者的研究,α=β=0.88,θ=2.25能够反映绝大部分决策者的行为偏好特征,故本文在后面的算例中将按以上建议值进行取值。
2.3 确定各指标的焦元构成由前景决策矩阵可知,前景值V(xij)表示决策者在既定的预期水平下,对第i个方案在指标j上的效用感知:V(xij)≥0,感知为收益; V(xij) < 0,则感知为损失。很显然,前景值V(xij)越大,表明决策者在指标j下选择方案i的可能性(概率分配值)越大。因此,若将方案在某一指标下的概率分配值看作一条证据,通过证据合成便可得到在综合考虑所有决策指标的情况下,该方案成为最优方案的可信度,最后,根据可信度的大小即可实现方案决策。按照这一思路,设定所有风险控制方案集为一个识别框架Θ,有如下定义:
定义1[14]:如果集函数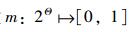
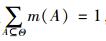
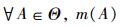
根据以上定义,需首先通过标准化处理,将前景决策矩阵中的元素(前景值)转换成[0, 1]之间的数。目前,常用的标准化处理方法通常有“最小-最大标准化”、“Z-score标准化”、“对数Logistic标准化”等。考虑到采用“最小-最大标准化”方法对指标前景值作标准化处理时,将使得每列指标下的最小前景值变为零,从而不能与指标值未知的情况形成有效区分, 而采用“Z-score标准化”方法将指标前景值转换成[-1, 1]之间的数,亦不满足要求, 故本文选用“对数Logistic标准化”方法对前景决策矩阵进行标准化处理:
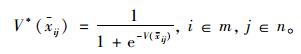
|
(10) |
V*=[V*(xij)]m×n为标准化处理后的前景决策矩阵。
定义2[15]:对于∀as, ar∈Θ,且as≠ar,如果V*(xsj)=V*(xrj)成立,j=1, 2, …, n,则称as和ar属于同一焦元。
由此,可以确定各决策指标的焦元构成,并将其表示为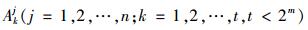
各决策指标焦元的基本概率分配值mj(Akj)可通过式(11)、(12)得到:
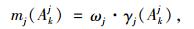
|
(11) |
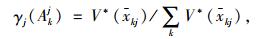
|
(12) |
式中,ωj为各决策指标的权重,可通过层次分析法求得,即将图 1中的9个决策指标两两相互比较,利用一个五标度表(如表 1所示)将比较结果数量化,由此得到一个判断矩阵,通过求解判断矩阵的特征向量便可得到各决策指标的权重ωj,且满足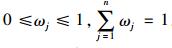
| 标度 | 两两因子相互比较的重要性说明 |
| 1 | 因子i与因子j一样重要,或因子与其自身比较 |
| 2 | 因子i比因子j稍微重要一点 |
| 3 | 因子i比因子j明显重要 |
| 4 | 因子i比因子j重要得多 |
| 5 | 因子i比因子j极其重要 |
| 1,1/2,1/3,1/4,1/5 | 分别对应于上述重要性的相反情况,即因子j比因子i重要的情况 |
由于客观事物的复杂性以及人们认识的局限性,以上得到在决策指标j下各焦元的基本概率分配值之和小于1,即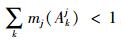
在得到单个决策指标下焦元的概率分配值之后,需通过证据合成运算,确定在综合考虑所有决策指标的情况下各焦元的概率分配值。由证据理论可知,当m1⊕m2⊕…⊕mn存在时,利用Dempster证据合成法则将多个基本概率分配值mj(Akj)合成为一个概率分配值m(Ak),其计算公式为:
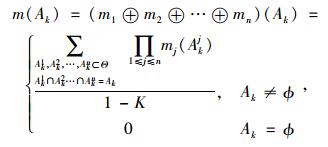
|
(13) |
式中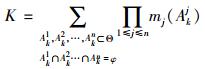
定义3[14]:设Θ是一个识别框架,A为识别框架Θ的任一子集,记作A⊆Θ,且满足Bel(A)=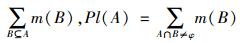
由以上定义,确定每个备选方案ai(i=1, 2, …, m)的信任度Bel({ai})和似真度Pl({ai})分别为:
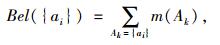
|
(14) |
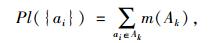
|
(15) |
则由Bel({ai})和Pl({ai})构成的备选方案ai的信度区间为:[Bel({ai}), Pl({ai})]。
2.6 方案排序各方案的信度区间反映了该方案成为最优方案的可信程度[15-16],因此,通过比较各方案的信度区间即可实现最优方案决策,其方法为:
对于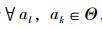
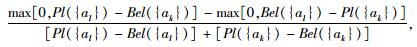
(1)P(al>ak)>0.5,则方案al优于ak,记作al>ak;
(2)P(al>ak) < 0.5,则方案al劣于ak,记作al<ak;
(3)P(al>ak)=0.5,则方案al与方案ak没有差别,记作al≈ak;
(4)对于任意3个方案al,ak,aq(l, k, q∈1, 2, …, m),若P(al>ak)>0.5,P(ak>aq)>0.5,则方案al优于aq,记作alak>aq。
由此便可得到所有风险控制方案ai(i=1, 2, …, m)的排序。
3 实例分析 3.1 工程概况及险情描述长沙地铁3号线一期工程某车站为地下二层岛式车站,车站外包尺寸210.2 m×20.7 m,采用明挖法施工,基坑开挖深度16.8~20.7 m,围护结构采用φ1 000@1 200钻孔灌注桩+一道钢筋混凝土支撑+三道φ609钢管支撑支护,桩间采用φ600旋喷桩嵌缝止水。根据《城市轨道交通岩土工程勘察规范》[17]的相关规定,该车站基坑工程重要性等级及工程安全等级均为一级,车站基坑施工监测平面布置如图 2所示。
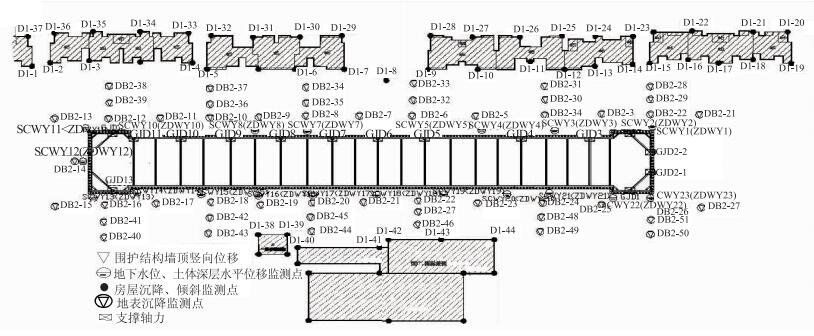
|
| 图 2 长沙地铁3号线某车站基坑施工监测平面图 Fig. 2 Monitoring layout of deep excavation constructionin a station of Changsha metro line 3 |
| |
2015年5月13日,在开挖车站东端盾构井至13 m深度时,在基坑转角处出现一处桩间土漏水的情况,由于当时水量不大,施工单位并没有予以足够重视。5月14、15日连续两天大雨致使原漏水处涌水量加大,水质浑浊,且在相邻桩间出现多处不同程度的涌水现象。地面沉降监测数据显示,沉降点DB2-1,DB2-2,DB2-3,DB2-29等沉降速率明显加快,最大沉降量达到30 mm,已超过风险预警值(28 mm)。针对以上险情,可采取的风险控制方案主要有以下3种:双液注浆止水(a1),高压旋喷桩止水(a2),冻结法止水(a3)。
3.2 方案决策险情发生后,项目部迅速会同业主、设计、监理等单位成立了专家组,根据图 1所示的深基坑施工风险控制方案决策指标体系,对以上3种方案进行指标评价,评价结果如表 2所示。
| 控制方案 | 决策指标 | ||||||||
| c1 | c2 | c3/元 | c4/h | c5 | c6 | c7 | c8 | c9 | |
| a1 | 0.85 | 低 | [0.2, 0.7] | [3,6] | 高 | 低 | 低 | 较低 | 高 |
| a2 | 0.7 | 中 | [0.7, 1.3] | * | 较高 | 中 | 非常低 | 较高 | 较低 |
| a3 | * | 非常低 | [0.9, 1.5] | [3,5] | 高 | 较高 | 较低 | 非常低 | 高 |
| 注:*表示方案在该项指标上的评价值未知 | |||||||||
由于专家组在进行方案决策时,不仅要对各方案进行指标评价,同时也会结合险情特点、施工条件等因素给出各决策指标的期望值,只不过这些期望值往往是通过下达指令、设定目标等方式体现出来的。针对本次险情,专家组给出的指标期望向量E={1.0,非常低,[0.5,5.0],[2, 4],高,中,中,较低,高}。同时,运用层次分析法得到各决策指标的权重W={0.15,0.2,0.03,0.14,0.2,0.05,0.04,0.12,0.07}。进一步,根据公式(1)、(2)对各方案的指标初始值以及指标期望值进行规范化处理,处理后的方案决策矩阵如表 3所示。
| xij | c1 | c2 | c3/万元 | c4/h | c5 | c6 | c7 | c8 | c9 |
| a1 | [0.5, 0.5] | [0.5, 0.75] | [0.9, 1] | [0, 0.75] | [0.5, 1] | [0.75, 1] | [0.5, 0.75] | [0.4, 0.6] | [0.75, 1] |
| a2 | [0, 0] | [0, 0.25] | [0.77, 0.9] | * | [0, 0.5] | [0.25, 0.5] | [0.75, 1] | [0, 0.2] | [0, 0.25] |
| a3 | * | [0.75, 1] | [0.73, 0.85] | [0.25, 0.75] | [0.5, 1] | [0, 0.25] | [0.25, 0.5] | [0.8, 1] | [0.75, 1] |
规范化的指标期望向量E={[1, 1],[0.75, 1],[0, 0.94],[0.5, 1],[0.5, 1],[0.25, 0.5],[0, 0.25],[0.4, 0.6],[0.75, 1]}。
由公式(3)~(9)得到备选方案的前景决策矩阵,如表 4所示。
| V(xij) | c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | c9 |
| a1 | -1.22 | -0.66 | 0.68 | -1.0 | 0 | 0.54 | 0.54 | 0 | 0 |
| a2 | -2.25 | -1.75 | 0.59 | * | -1.22 | 0 | 0.78 | -1.0 | -1.75 |
| a3 | * | 0 | 0.56 | -0.66 | 0 | -0.66 | 0.30 | 0.45 | 0 |
根据定义2,将某一指标下的相同前景值合并为同一焦元,并运用公式(10)~(12)计算各指标所含焦元的基本概率分配值,结果如表 5所示。
| 指标 | 焦元构成及概率分配值 | |||
| c1 | m1({a1})= 0.106 |
m1({a2})= 0.044 |
m1({Θ})= 0.85 |
|
| c2 | m2({a1})= 0.069 |
m2({a2})= 0.03 |
m2({a3})= 0.101 |
m2({Θ})= 0.8 |
| c3 | m3({a1})= 0.01 |
m3({a2})= 0.009 |
m3({a3})= 0.008 |
m3({Θ})= 0.97 |
| c4 | m4({a1})= 0.062 |
m4({a3})= 0.078 |
m4({Θ})= 0.86 |
|
| c5 | m5({a1a3})= 0.082 |
m5({a2})= 0.037 |
m5({Θ})= 0. 882 |
|
| c6 | m6({a1})= 0.022 |
m6({a2})= 0.017 |
m6({a3})= 0.012 |
m6({Θ})= 0.95 |
| c7 | m7({a1})= 0.013 |
m7({a2})= 0.015 |
m7({a3})= 0.012 |
m7({Θ})= 0.96 |
| c8 | m8({a1})= 0.044 |
m8({a2})= 0.023 |
m8({a3})= 0.053 |
m8({Θ})= 0.88 |
| c9 | m9({a1a3})= 0.031 |
m9({a2})= 0.009 |
m9({Θ})= 0.96 |
|
由公式(13)~(15)进行证据合成,得到各方案的信度区间分别为:方案a1[0.382, 0.519];方案a2[0.189, 0.228];方案a3[0.292, 0.429]。由方案排序规则可知,a1>a3>a2,即采用双液注浆止水为最优风险控制方案。
3.3 不完全信息对方案决策的影响为了分析不完全信息对方案决策的影响,将表 2中某项已知的指标评价值换成未知信息,分析由此造成各方案信度区间的变化。囿于篇幅限制,本文仅以方案a1产生次生灾害的可能性指标为例进行分析。假设决策者对方案a1产生次生灾害的可能性未知,其他条件保持不变,运用本文方法重新计算各方案的信度区间分别为:方案a1[0.267, 0.439];方案a2[0.206, 0.281];方案a3[0.356, 0.528]。由排序规则可知,a3>a1>a2。由计算结果不难发现,除了方案a1的可信度减小之外,方案a2, a3的可信度均有不同程度的增加。究其原因是当指标值x12由已知变为未知时,引起指标c2的焦元构成及其概率分配值发生重分布:m2({a2})=0.046,m2({a3})=0.154,m5({Θ})=0.8。此时,方案a1在指标c2上的可信度由0.069变为零,而方案a2的可信度由0.03增加到0.046,方案a3的可信度由0.101增加到0.154,以上是导致方案排序发生变化的最根本原因。另外,从各方案信度区间变化的绝对值来看,方案a1信度区间变化的绝对值最大,说明当某方案的指标评价信息发生变化时,所有方案的信度均会受到一定程度的影响,但受影响最大的是该方案本身。
3.4 不同决策方法的比较分析为了进一步验证本文所提方法的合理性,分别采用文献[6]提出的基于证据推理和逼近理想解排序的方法、文献[18]的模糊层次分析法,以及文献[19]提出的基于累积前景理论的决策方法对上述问题进行应急决策,决策结果如表 6所示。需要说明的是,采用文献[6]的方法时,决策部门数目取1,正理想解向量θ+={1,非常低,[0.1, 0.1],[1, 1],非常高,非常低,非常低,非常低,非常高},负理想解向量θ-={0.5,非常高,[5, 5],[8, 8],非常低,非常高,非常高,非常高,非常低}。采用文献[18]以及文献[19]的方法时,指标评价值x31=[0.7, 0.9],x24=[4, 8],其他指标评价值同表 2。
由表 6可知,本文提出的方法与文献[18-19]的决策结果相同,说明运用本文所提方法进行深基坑施工风险控制方案决策具有一定的可行性。另外,运用文献[18-19]方法进行方案决策时,要求所有方案的指标评价值必须为已知信息,而本文方法并没有此限制。尽管文献[6]的方法同样适用于信息不完全情况下的方案决策,但本文方法与文献[6]的方法在方案a1及方案a3的排序上却存在差别。其主要原因是本文以决策者的合理期望值为参照点对各方案的优劣进行评价,而文献[6]的方法是以绝对的最优、最劣值作为理想参照点进行方案决策。显然,对比不同方法的决策结果可知,本文提出的方法更具有合理性。
4 结论为了能在深基坑施工处于危机状态时,对深基坑施工风险控制方案进行迅速、合理的决策,本文提出一种将前景理论与证据理论相结合的深基坑施工风险控制方案决策方法。该方法的实质是在建立深基坑施工风险控制方案决策指标体系的基础上,以决策者的合理期望值为参照点,对各备选方案的优劣进行评价。但考虑到评价信息的不完全性,本文将各方案的指标前景值作为证据,从各方案成为最优方案的可信度的角度,通过证据合成得到各方案的信度区间,比较信度区间的大小实现最优方案决策。将上述决策方法应用于一个具体的工程实例,得到以下结论:
(1)运用证据理论对深基坑施工风险控制方案进行决策不受指标评价信息完全与否的限制。当指标评价矩阵中的某个已知的指标评价值变为未知时,引起相应指标的焦元构成及其概率分配值发生重分布,进而对深基坑施工风险控制方案的决策结果产生一定程度的影响。另外,从各方案信度区间变化的绝对值来看,所有备选方案的信度区间均会发生不同程度的变化,但与该指标值对应的方案信度区间变化程度最大。因此,通过多方面搜集方案的评价信息,减少未知信息的数目,是提高方案可信度的重要途径。
(2)将前景理论用于深基坑施工风险控制方案决策考虑了决策者对工程的合理期望,相对于以绝对最优、最劣值作为理想参照点进行方案决策的方法更具有合理性。
| [1] | 魏道江, 李慧民. 运用投影寻踪及信息扩散理论评价深基坑施工风险[J]. 中国安全科学学报 , 2015, 25 (2) : 147-152 WEI Dao-jiang, LI Hui-min. Risk Dynamic Assessment for Deep Excavation Based on Projection Pursuit and Information Diffusion Theory[J]. China Safety Science Journal , 2015, 25 (2) : 147-152 |
| [2] | 李宏安, 冯雨润之, 李玲利, 等. 基于数值模拟的福州某地铁站基坑地下水控制方案研究[J]. 公路交通科技 , 2016, 31 (2) : 88-95 LI Hong-an, FENGYU Run-zhi, LI Ling-li, et al. Research of Foundation Pit Groundwater Control Scheme of a Metro Station in Fuzhou Based on Numerical Simulation[J]. Journal of Highway and Transportation Research and Development , 2016, 31 (2) : 88-95 |
| [3] | 王鸣晓. 模糊综合评判法在基坑工程风险评估中的应用[J]. 公路交通科技 , 2011, 28 (6) : 57-61 WANG Ming-xiao. Application of Fuzzy Comprehensive Evaluation Method in Risk Assessment of Excavation Engineering[J]. Journal of Highway and Transportation Research and Development , 2011, 28 (6) : 57-61 |
| [4] | 钱七虎, 戎晓力. 中国地下工程安全风险管理的现状、问题及相关建议[J]. 岩石力学与工程学报 , 2008, 27 (4) : 649-655 QIAN Qi-hu, RONG Xiao-li. State, Issues and Relevant Recommendations for Security Risk Management of China's Underground Engineering[J]. Chinese Journal of Rock Mechanics and Engineering , 2008, 27 (4) : 649-655 |
| [5] | 蒋风光, 李鹏, 陈立文. 基于MYCIN不确定因子的区间灰数应急决策方法[J]. 运筹与管理 , 2015, 24 (4) : 30-35 JIANG Feng-guang, LI Peng, CHEN Li-wen. Interval Grey Numbers Emergency Decision-making Methods Based on MYCIN Uncertainty Factor[J]. Operations Research and Management Science , 2015, 24 (4) : 30-35 |
| [6] | 吴兵, 严新平, 汪洋, 等. 不确定性信息下的内河失控船应急决策方法[J]. 哈尔滨工程大学学报 , 2016, 37 (7) : 1-7 WU Bing, YAN Xin-ping, WANG Yang, et al. Emergency Decision-making Method for Handling an Out-of-control Ship in Inland Water in Case of Uncertain Information[J]. Journal of Harbin Engineering University , 2016, 37 (7) : 1-7 |
| [7] | 樊治平, 刘洋, 沈荣鉴. 基于前景理论的突发事件应急响应的风险决策方法[J]. 系统工程理论与实践 , 2012, 32 (5) : 977-984 FAN Zhi-ping, LIU Yang, SHEN Rong-jian. Risk Decision Analysis Method for Emergency Response Based on Prospect Theory[J]. Systems Engineering-Theory & Practice , 2012, 32 (5) : 977-984 |
| [8] | 刘明, 张培勇, 萧毅鸿. 应急不完全信息环境下的混合多属性协同决策方法[J]. 数学的实践与认识 , 2012, 42 (22) : 100-110 LIU Ming, ZHANG Pei-yong, XIAO Yi-hong. Hybrid Multi-Attribute and Collaborative Decision-Making Method Under an Emergency and Incomplete Information Environment[J]. Mathematics in Practice and Theory , 2012, 42 (22) : 100-110 |
| [9] | 郑晶, 王应明, 叶歆. 考虑应急方案总体优势度的决策方法[J]. 控制与决策 , 2015, 30 (7) : 1239-1244 ZHENG Jing, WANG Ying-ming, YE Xin. Decision Method for Emergency Alternative with Considering Total Superiority Degree[J]. Control and Decision , 2015, 30 (7) : 1239-1244 |
| [10] | 王亚琼, 周绍文, 孙铁军, 等. 基于非对称贴近度的在役隧道衬砌结构健康诊断方法[J]. 现代隧道技术 , 2015, 52 (2) : 52-58 WANG Ya-qiong, ZHOU Shao-wen, SUN Tie-jun, et al. A Diagnosis Method for Lining Structure Conditions of Operated Tunnels Based on Asymmetric Closeness Degree[J]. Modern Tunnelling Technology , 2015, 52 (2) : 52-58 |
| [11] | ISHIBUCHI H, TANAKA H. Multiobjective Programming in Optimization of the Interval Objective Function[J]. European Journal of Operational Research , 1990, 48 (2) : 219-225 |
| [12] | BIRNBAUM M H. Three New Tests of Independence that Differentiate Models of Risky Decision Making[J]. Management Science , 2005, 51 (9) : 1346-1358 |
| [13] | HE Xue-dong, ZHOU Xun-yu. Portfolio Choice under Cumulative Prospect Theory:An Analytical Treatment[J]. Management Science , 2011, 57 (2) : 315-331 |
| [14] | SHAFER G. A Mathematical Theory of Evidence[M]. Princeton: Princeton University Press, 1976 . |
| [15] | 谭鑫, 王炜, 张茂军. 不完备信息条件下基于证据理论的CGF行为决策方法[J]. 系统工程理论与实践 , 2013, 33 (6) : 1608-1614 TAN Xin, WANG Wei, ZHANG Mao-jun. Behavior Decision Method of CGF with Incomplete Information Based on Evidence Theory[J]. Systems Engineering-Theory & Practice , 2013, 33 (6) : 1608-1614 |
| [16] | 姚爽, 郭亚军, 黄玮强. 一种语言评价信息不完全的多属性群决策方法[J]. 系统工程学报 , 2011, 26 (4) : 460-467 YAO Shuang, GUO Ya-jun, HUANG Wei-qiang. An Approach of Multi-attribute Group Decision Making with Incomplete Linguistic Assessment Information[J]. Journal of Systems Engineering , 2011, 26 (4) : 460-467 |
| [17] | GB50307-2012, 城市轨道交通岩土工程勘察规范[S]. GB50307-2012, Code for Geotechnical Engineering Investigation of Urban Railway Transit[S]. |
| [18] | 周罕, 曹平. 软土地区城市深基坑支护方案优选的模糊层次分析法[J]. 中南大学学报:自然科学版 , 2012, 43 (9) : 3582-3588 ZHOU Han, CAO Ping. A Fuzzy AHP Approach to Select Supporting Schemes for City Foundation Pit in Soft Soil[J]. Journal of Central South University:Science and Technology Edition , 2012, 43 (9) : 3582-3588 |
| [19] | 樊治平, 陈发动, 张晓. 基于累积前景理论的混合型多属性决策方法[J]. 系统工程学报 , 2012, 27 (3) : 295-301 FAN Zhi-ping, CHEN Fa-dong, ZHANG Xiao. Method for Hybrid Multiple Attribute Decision Making Based on Cumulative Prospect Theory[J]. Journal of Systems Engineering , 2012, 27 (3) : 295-301 |
 2017, Vol. 34
2017, Vol. 34
