扩展功能
文章信息
- 方薇, 陈向阳, 杨果林
- FANG Wei, CHEN Xiang-yang, YANG Guo-lin
- 带齿格栅加筋挡墙工作机理的数值模拟研究
- Numerical Simulation of Working Mechanism of Retaining Wall Reinforced with Denti-geogrid
- 公路交通科技, 2017, 34(1): 32-38
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 32-38
- 10.3969/j.issn.1002-0268.2017.01.005
-
文章历史
- 收稿日期: 2015-12-30
2. 中南大学 土木工程学院, 湖南 长沙 410075
2. School of Civil Engineering, Central South University, Changsha Hunan 410075, China
近年来,土工加筋技术迅速发展,其应用范围日益广泛,但总地说来,加筋形式仍以水平加筋为主,相关设计理论与施工方法也主要集中在这一方面。最近,一些学者对于新型加筋结构进行了研究,如参考文献[1-6]。为了增强空间加筋效应,张孟喜[7]提出了一种立体加筋方式:水平-竖向组合式(H-V)加筋,进一步地,该课题组设计了非满布多层H-V加筋黏土的试验方案[8],以镀锌铁皮和有机玻璃为加筋材料进行了44组固结不排水三轴剪切试验,研究了加筋黏性土的应力-应变关系、强度特性及破坏形态,探讨了不同加筋高度、不同围压及不同筋材对加筋黏土强度的影响。接着,魏伟[9]针对不同的水平筋形式(带孔、满布)、竖筋高度以及不同围压下的水平-竖向(H-V)加筋砂土,通过平面应变试验研究了不同的水平筋形式对H-V加筋砂土强度的影响;孙亮富[10]结合道路软基室内模型试验,对比研究了不同齿筋形式对双向网格状带齿加筋效果的影响。在数值模拟方面,张陶陶[11]利用ABAQUS软件对纯砂地基、水平加筋地基和H-V加筋地基进行了模拟,分析了H-V加筋地基对地基承载力的影响,考察了地基中塑性区的发展演变情况。彭明远[12]等对于组合式加筋土挡墙土-筋相互作用机理进行了二维有限元分析,对于土筋相互作用特性进行了有益探讨,在建模中采用了梁单元模拟筋材。周淮[13]采用颗粒流软件研究了H-V加筋挡墙承载力试验,得到了挡墙变形和竖筋侧应力的相关数据。
众所周知,土工合成材料与填土的界面作用特性直接决定着加筋土工程的内部稳定性,设计人员需要通过接触面摩擦特性试验为加筋土工程应用提供设计参数,从而为其稳定性与变形分析提供依据。在工程应用中,通常通过室内摩擦(剪切)试验、拉拔试验或现场足尺试验等方法来测定加筋的摩擦特性。作为室内模型试验,前两种试验的强度发挥和主要影响因素不同。一般认为:若双面与土均发生相对位移,则拉拔试验更合适;对刚度较大的材料也是采用拉拔试验更为恰当。另外,若筋材空隙较大并且有一定的厚度,土与土之间的剪切将占很大比例,这时同样应采用拉拔试验来研究接触面的界面特性。
综上所述,水平-竖向组合式三维加筋结构是一种新颖而有效的结构类型,它在传统水平筋条的基础上设置与之垂直的竖向筋条,使得在水平筋材提供摩擦阻力的同时,竖向筋材对土体相对变形产生较大的法向约束作用,从而显著地提高了土体强度,然而目前关于其作用机理、工作性态、计算模型等方面的研究成果还十分欠缺。因此,本文拟针对“格栅+横挡”(带齿格栅)这一新型组合式加筋结构进行研究,利用Flac3D有限差分程序模拟其拉拔试验过程,对其工作机理和性态以及主要影响因素进行分析,进而提出相关概化计算模型。
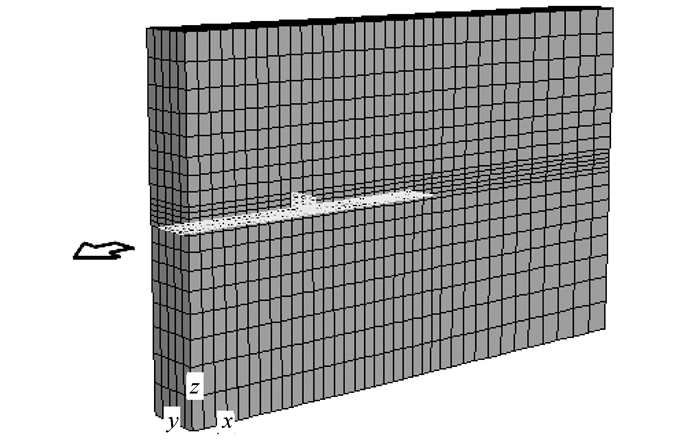
1 带齿格栅拉拔试验的数值模拟 1.1 计算条件与参数选取模型尺寸为11 m (长)×1.2 m (宽)×7 m (高),格栅尺寸为6 m (长)×0.72 m (宽),横挡与格栅同宽,如图 1所示,其中土体采用brick实体单元模拟,水平土工格栅采用geogrid结构单元模拟。由于geogrid单元通常用以抵抗剪切而非弯曲作用,而shell单元又不能用以模拟筋材与土体之间的滑移,故采用liner结构单元模拟齿筋。
|
| 图 1 单层H-V加筋结构示意图 Fig. 1 Schematic diagram of reinforcement with single H-V layer |
| |
模型单元数为36(长)×5(宽)×21(高),计算采用摩尔-库仑模型。边界条件:底面固定,左右前后均为水平约束,顶面为自由边界。重力加速度取9.81 m/s2,在模型顶面施加法向均布荷载,达到平衡后在筋材外端施加拉拔力,拉拔速率恒定为2×10-3mm/时步,共计算100 000时步,即拉拔位移为0.2 m。此外,数值模拟中还需用到的参数如表 1~表 3所示,表中部分参数意义如下:t为厚度;cs_sk、cs_scoh、cs_sfric、cs_scohres分别为切向连接弹簧的刚度、黏聚力、内摩擦角和残余应力;cs_nk、cs_ncut分别为法向连接弹簧的刚度、拉伸强度。
| w/% | ρ/(g·cm-3) | c/kPa | φ/(°) | K/MPa | G/MPa |
| 14.65 | 1.8 | 30.0 | 25.0 | 21.3 | 8.71 |
| E/GPa | μ | t/mm | cs_sk/(MN·m-3) | cs_scoh/kPa | cs_sfric/(°) |
| 20 | 0.33 | 3.5 | 2.8 | 9.3 | 16.4 |
| E/GPa | μ | t/mm | cs_nk/(MN·m-3) | cs_sk/(MN·m-3) | cs_ncut/kPa | cs_scoh/kPa | cs_scohres/kPa | cs_sfric/(°) |
| 25 | 0.15 | 30 | 800 | 800 | 4 000 | 4 000 | 2 000 | 20 |
1.2 齿筋的模拟
水平-竖向组合式筋材本身是一个整体,竖向齿筋的下端和水平格栅是融为一体的,所以在数值模拟中,齿筋下沿与格栅共用一排节点,且允许齿筋在拉拔过程中绕其发生转动。
另外,为了实现节点共享,需采用“冗余构造-消去”的方法,即首先比目标高度多建立一层起辅助作用的liner单元;然后,将原先自动生成的底层linersel单元全部删除,取而代之的是人为构造的一层linersel单元,它们将用次底层及与格栅交线上的节点来共同定义;最后将冗余的辅助性liner单元消去。
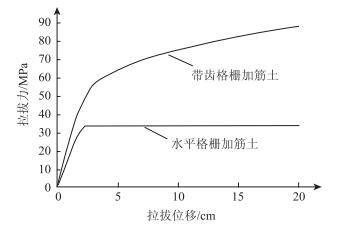
2 带齿格栅挡墙的工作性态 2.1 拉拔过程曲线初始条件:竖向荷载20 kPa,格栅埋深3.5 m,横挡高0.1 m,位于格栅中部。拉拔过程曲线如图 2所示(为了便于对比,也给出了无齿筋时的计算结果)。可见,当拉拔位移达到一定值时,拉拔曲线逐步趋向平缓。此外,带齿格栅的拉拔力远远高于普通土工格栅(无齿筋),拉拔位移为0.2 m时对应的拉拔力为88.1 kPa,而普通格栅的拉拔力为33.8 kPa。
|
| 图 2 拉拔曲线(拉拔位移0.2 m) Fig. 2 Pullout curves (0.2 m pullout displacement) |
| |
一般认为:拉拔曲线大致可以分为3个阶段:(1)快速增长阶段:当筋材与土体之间相对位移很小时,抗拔阻力(由咬合力、摩擦力和黏聚力3部分组成)尚未充分发挥,抗拔阻力随位移的增大而增大。在靠近拉拔力源端处的相对位移较大,抗拔力也较大,远处随相对位移减小抗拔力也逐渐减小,此时筋材有一定长度未发挥出阻力作用而处于空闲状态。在此阶段,总抗拔力随拔出位移的变化由两种因素组成:一方面是作用长度不断增大;另一方面是作用长度范围内的阻力随相对位移的增大而增大,使拉拔力随拔出位移的增大而迅速上升。(2)稳定发展阶段:随着拔出位移的增大,筋材与土体间相对位移不断增加,邻近土体中微裂缝不断发展,抗拔阻力逐渐得到充分发挥,并达到峰值。(3)筋材屈服阶段:随土体中微裂缝不断增多,整个筋材都处于残余阻力状态,总抗拔力随位移增大而保持基本不变。由于计算时步所限(×105时步),带齿格栅的拉拔力尚未达到峰值,而无齿筋格栅在约2.5 cm拉拔位移后就处于屈服阶段。
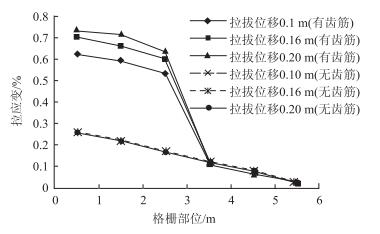
2.2 筋材变形情况图 3给出了格栅不同部位的拉应变分布情况,图中横坐标表示离拉拔端的距离。可以看出,无齿筋时3条虚线是完全重合的,这表明此时各处拉应变是恒定不变的,同时,从外至里格栅拉应变呈线性减小的趋势。有齿筋时曲线均呈“S”形,齿筋部位正是拉应变变化的“分水岭”,即:拉拔过程中齿筋外侧的拉应变增长较为显著,而齿筋内侧不同部位的拉应变没有明显变化,这表明拉拔应力的衰减主要发生在齿筋外侧的格栅部位,从而使远离拉拔端的格栅拉应变大大减小。
|
| 图 3 筋材不同部位的拉应变 Fig. 3 Tensile strain of reinforcement segments |
| |
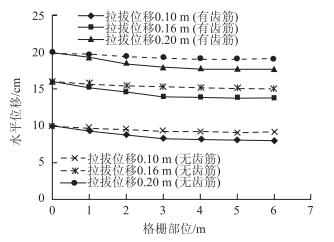
数值模拟表明:由于土体与筋材之间的摩擦效应,齿筋内侧的拉拔位移小于外侧, 如图 4所示。摩阻力越大,格栅末端的位移值越小。筋材受拉拔力作用发生变形时,并不是以同样的速率向外移动,而是沿筋材向里变形速率呈非线性减小的形态,100 000时步后格栅上的最大、最小拉拔位移分别为20 cm和17.7 cm。此外,由于齿筋的存在,格栅水平位移较无齿筋时要小一些,齿筋内侧尤为显著。
|
| 图 4 筋材不同部位的水平位移 Fig. 4 Horizontal displacement of reinforcement segments |
| |
此外,拉拔过程中的筋材变形情况如图 5所示,图中显示的变形已被放大100倍。可见,随着拉拔距离的增加,筋材在发生向外平动的同时,也出现了齿筋的后倾及抬升。

|
| 图 5 筋材变形过程 Fig. 5 Deformation process of reinforcement |
| |
2.3 土体应力场和变形场
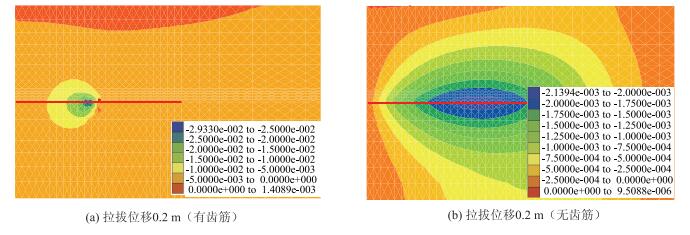
拉拔试验后的土体水平位移场如图 6所示。可见:有齿筋时,位移场梯度明显较大。位移场核心位于齿筋外侧25 cm左右。随着拉拔的进行,土体沿拉拔方向的水平位移逐渐增大,最终水平位移峰值约为3 cm,等位移线大致呈圆形。无齿筋时,最大位移发生在距离格栅后缘约L/3处(L为格栅长度),且等位移线大致呈纺锤形,这表明普通格栅加筋结构较易发生拉拔破坏,筋材拔出过程中土体对其约束作用很有限。
|
| 图 6 土体水平位移场(单位:m) Fig. 6 Horizontal displacement field of soil (unit:m) |
| |
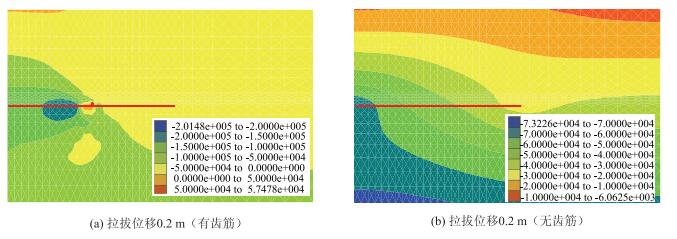
拉拔试验后的土体水平应力场如图 7所示。可见:拉拔过程中模型左下部以水平压应力为主,但由于齿筋后倾造成格栅联结部位向上抬升,紧邻齿筋的外侧土体出现了一处较小的拉应力区,应力集中现象较为显著。对于无齿筋的普通格栅,水平应力分布较为均匀,应力梯度较小,土体中的水平应力等值线在拉拔力的影响下向左下方凸起。
|
| 图 7 土体水平应力场(单位:Pa) Fig. 7 Horizontal stress field of soil (unit:Pa) |
| |
3 带齿格栅拉拔试验的影响因素研究
实际工程中,拉拔试验的结果取决于很多因素。对于普通格栅,常见的影响因素有土性、压实度、含水量、上部荷载、拉拔速度、边界条件、筋材埋入长度、筋材属性等,关于它们已有许多学者进行了研究。显然,对于带齿格栅,影响因素更为繁多。为了凸显“齿筋”这一特点,同时使问题得到简化,以下仅讨论齿筋布置参数对于拉拔试验的影响,本文主要考虑了以下4个参数(其余参数与前文一致):(1)齿筋与拉拔端距离d;(2)齿筋间距s(居中布置两道齿筋);(3)齿筋高度h;(4)齿筋厚度t。相应的数值模拟结果如表 4所示。
| 影响因素 | 参数取值 | 最大拉拔力/kPa |
| 齿筋与拉拔端距离d/m | 1 | 85.32 |
| 2 | 85.79 | |
| 3 | 88.06 | |
| 4 | 86.76 | |
| 5 | 85.83 | |
| 齿筋间距s/m | 0.5 | 103.9 |
| 1.0 | 117.3 | |
| 1.5 | 119.1 | |
| 2.0 | 120.8 | |
| 2.5 | 122.0 | |
| 齿筋高度h/m | 0.1 | 88.06 |
| 0.2 | 94.74 | |
| 0.3 | 101.3 | |
| 齿筋厚度t/cm | 1 | 88.00 |
| 2 | 88.02 | |
| 3 | 88.06 |
从表 4可知:
(1)齿筋与拉拔端距离对拉拔力的影响不是单调的,由于边界条件影响,当齿筋离模型侧边界距离约3 m时,拉拔力达到峰值。
(2)齿筋间距与拉拔力呈正相关,即随着齿筋间距增加,总拉拔力也是增加的。这是因为若齿筋间距过小,则前后齿筋作用长度将出现一定范围的重叠,造成材料的浪费;当齿筋间距逐渐增大时,齿筋的作用长度都将得到充分开展,每条齿筋的抗力都能充分发挥出来,因此拉拔力将增大;当齿筋间距超过某一阀值时,拉拔力将逐渐停止增长。
(3)齿筋高度与拉拔力同样呈正相关,齿筋提供的阻力随着其面积的增加而增加,但高度的增加与材料加工工艺、实际施工难度有着密切关联,因此一味地增加齿筋高度是没有意义的,以常见的土工格室为例,其合适的高度区间约为5~20 cm。
(4)齿筋厚度对拉拔力的影响极小,当齿筋厚度从1 cm增至3 cm时,拉拔力增大约0.07%。
4 带齿格栅的工作机理与概化模型 4.1 带齿格栅的工作机理根据前文所述,可以尝试阐述带齿格栅工作机理如下:
(1)挤密阶段:在拉拔初期的很短时间内,齿筋前方土体被挤密而得到强化。
(2)绕流阶段:随着拉拔的进行,齿筋在土体抗力下后倾,最终齿筋前方土体发生剪切破坏,由于摩擦角的存在,齿筋前部将有一楔形土块随着齿筋移动,与齿筋保持相对静止。土颗粒逐渐从“楔形块-齿筋”组合体上沿越过。另一方面,原本处于齿筋背后的土颗粒由于齿筋的前移而松散开来,并在自重和相邻土颗粒的推挤作用下重新分布。在绕流过程中,绕流土体必然会对“楔形块-齿筋”组合体产生阻力,即绕流阻力。因此,带齿筋材的拉拔阻力包括水平筋提供的阻力和齿筋提供的绕流阻力。
(3)稳定阶段:随着拉拔过程的完成,土体基本稳定下来,但齿筋前方楔形块上仍存在一个软弱面,它既是先期拉拔过程中的破坏面,也是以后继续拉拔时的潜在滑面。值得说明的是,以上3个阶段并非相互割裂的,而是一个逐步转化的过程。
4.2 带齿格栅的概化模型带齿格栅的概化模型基于以下假定:(1)筋材强度和刚度很大(可视为刚体),筋材变形可以忽略不计,且齿筋与格栅的连接在拉拔过程中不会失效[14]。筋材自重、厚度均可忽略不计。(2)土体为理想的莫尔-库仑材料,忽略齿筋背部土压力作用。(3)忽略尺寸效应,主要包括筋材拉拔宽度(图 1中的y方向)、齿筋间距、模型边界等条件对拉拔过程的影响。
于是,平面应变条件下的带齿格栅概化模型可简化表示为图 8。图中,T1,T2分别为格栅外端和内端所受拉力;根据极限应力圆相关知识,滑裂面与大主应力平面之间的夹角(即楔形块上方夹角)α=π/4+φ/2(φ为内摩擦角);f1为土体对水平格栅的摩擦阻力;f2为绕流土体对楔形土块的摩擦力;p1,p2分别为相应界面上的法向应力。

|
| 图 8 带齿格栅概化模型 Fig. 8 Generalized model of denti-geogrid |
| |
4.3 带齿格栅的极限拉拔力
根据图 8,若填料重度为γ,外部垂直均布荷载为p,黏聚力和内摩擦角为c和φ,筋材长度为L,埋深为H (远大于齿筋高度h),筋材与填料间的摩擦系数为μ,考察时取单位宽度,则有:
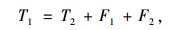
|
(1) |
式中,F1为水平格栅上下界面受到的摩擦阻力;F1=μ(γH+p)(2L-htan α);F2为“齿筋+楔形土块”受到的绕流阻力:
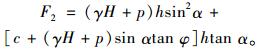
|
(2) |
对于最简单的单层齿筋情形,可以得到极限拉拔力T为:
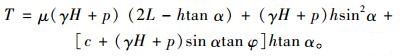
|
(3) |
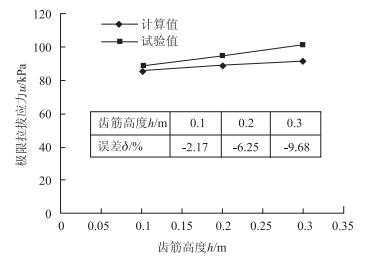
对于前文不同高度齿筋的情形,可以算得极限拉拔应力理论值。取μ=0.35,其余计算参数同前,计算值和数值试验结果的对比如图 9所示。可见:(1)计算值与模拟结果的变化趋势基本一致,只是随着齿筋高度的增加,模拟结果逐渐高出计算值;(2)将数值模拟结果与相应计算值对比,误差都在10%以内,平均误差为6.0%,表明本文提出的极限拉拔力模型的计算值与数值模拟结果基本吻合,模型具有一定的合理性。
|
| 图 9 拉拔力计算模型的验证 Fig. 9 Verification of pullout force calculation model |
| |
5 结论
本文利用Flac3D有限差分程序对于带齿格栅拉拔试验进行了数值模拟分析,研究了带齿格栅挡墙的工作机理和工作性态,分析了拉拔试验的影响因素,提出了带齿格栅概化模型,并进一步给出了极限拉拔力的计算方法。本研究的主要结论如下:
(1)带齿格栅拉拔应力的衰减主要发生在齿筋外侧。随着拉拔距离的增加,筋材在发生向外平动的同时,也出现了齿筋的后倾及抬升。有齿筋时,位移场梯度明显较大。拉拔过程中模型左下部以水平压应力为主,但由于齿筋后倾造成格栅联结部位向上抬升,紧邻齿筋的外侧土体出现了一处较小的拉应力区。
(2)由于边界条件影响,当齿筋离模型箱侧边界距离约3 m时,拉拔力达到峰值。若齿筋间距过小,则前后齿筋作用长度将出现一定范围的重叠,造成材料的浪费;当齿筋间距逐渐增大时,齿筋的作用长度都将得到充分开展,每条齿筋的抗力都能充分发挥出来,因此拉拔力将增大;当齿筋间距超过某一阀值时,拉拔力将逐渐停止增长。齿筋高度与拉拔力同样呈正相关,齿筋厚度对拉拔力的影响极小。
(3)拉拔过程可由挤密阶段、绕流阶段和稳定阶段加以描述,这3个阶段并非相互割裂的,而是逐步转化的。由带齿格栅概化模型算得的极限拉拔应力理论值与数值模拟结果基本一致,表明该模型具有一定的合理性。
| [1] | SAYEED M M A, RAMAIAH B J, RAWAL A. Interface Shear Characteristics of Jute/Polypropylene Hybrid Nonwoven Geotextiles and Sand Using Large Size Direct Shear Test[J]. Geotextiles and Geomembranes , 2014, 42 (1) : 63-68 |
| [2] | LAJEVARDI S H, DIAS D, RACINAIS J. Analysis of Soil-welded Steel Mesh Reinforcement Interface Interaction by Pull-out Tests[J]. Geotextiles and Geomembranes , 2013, 40 (5) : 48-57 |
| [3] | ZHU H H, ZHANG C C, TANG C S, et al. Modeling the Pullout Behavior of Short Fiber in Reinforced Soil[J]. Geotextiles and Geomembranes , 2014, 42 (4) : 329-338 |
| [4] | 黄向京, 方薇. 格宾材料在红砂岩填料中的拉拔试验研究[J]. 公路交通科技 , 2009, 26 (9) : 26-31 HUANG Xiang-jing, FANG Wei. Study on Pull-out Test of Gabion Reinforcement Filled with Red Sandstone[J]. Journal of Highway and Transportation Research and Development , 2009, 26 (9) : 26-31 |
| [5] | 李建, 唐朝生, 王德银, 等. 基于单根纤维拉拔试验的波形纤维加筋土界面强度研究[J]. 岩土工程学报 , 2014, 36 (9) : 1696-1704 LI Jian, TANG Chao-sheng, WANG De-yin, et al. Single Fiber Pullout Tests on Interfacial Shear Strength of Wave-shape Fiber-reinforced Soils[J]. Chinese Journal of Geotechnical Engineering , 2014, 36 (9) : 1696-1704 |
| [6] | 张建龙, 冼家驹, 赵斌斌, 等. 钢带式加筋挡土墙受力与变形监测研究[J]. 工程勘察 , 2015, 43 (8) : 21-25 ZHANG Jian-long, XIAN Jia-ju, ZHAO Bin-bin, et al. Monitoring Study on Stress and Deformation of Reinforcement Retaining Wall[J]. Geotechnical Investigation & Surveying , 2015, 43 (8) : 21-25 |
| [7] | 张孟喜, 闵兴. 单层立体加筋砂土性状的三轴试验研究[J]. 岩土工程学报 , 2006, 28 (8) : 931-936 ZHANG Meng-xi, MIN Xing. Triaxial Tests on Sand Reinforced with One-layer 3D Reinforcement[J]. Chinese Journal of Geotechnical Engineering , 2006, 28 (8) : 931-936 |
| [8] | 张孟喜, 张贤波, 段晶晶. H-V加筋黏性土的强度与变形特性[J]. 岩土力学 , 2009, 30 (6) : 1563-1568 ZHANG Meng-xi, ZHANG Xian-bo, DUAN Jing-jing. Strength and Deformation Properties of H-V Reinforced Clay[J]. Rock and Soil Mechanics , 2009, 30 (6) : 1563-1568 |
| [9] | 魏伟, 张孟喜, 张朕磊. 水平筋形式对水平-竖向加筋砂土强度的影响[J]. 上海大学学报:自然科学版 , 2011, 17 (2) : 196-202 WEI Wei, ZHANG Meng-xi, ZHANG Zhen-lei. Influence of Horizontal Reinforcement Forms on Strength of Sand Reinforced with Horizontal-Vertical Inclusions[J]. Journal of Shanghai University:Natural Science Edition , 2011, 17 (2) : 196-202 |
| [10] | 孙亮富, 张孟喜. 齿筋形式对加筋效果影响的对比试验[J]. 上海大学学报:自然科学版 , 2012, 18 (6) : 640-644 SUN Liang-fu, ZHANG Meng-xi. Comparative Experiments on Reinforcement Effects of Denti-Inclusion Forms[J]. Journal of Shanghai University:Natural Science Edition , 2012, 18 (6) : 640-644 |
| [11] | 张陶陶, 张孟喜, 侯娟. 基于有限元强度折减法的H-V加筋地基破坏机理[J]. 上海交通大学学报 , 2011, 45 (5) : 757-761 ZHANG Tao-tao, ZHANG Meng-xi, HOU Juan. Bearing Capacity Behavior and Failure Modes of H-V Reinforcement Foundation Based on Strength Reduction Finite Element Method[J]. Journal of Shanghai Jiaotong University , 2011, 45 (5) : 757-761 |
| [12] | 彭明远, 黄超, 彭基敏, 等. 水平-竖向组合式加筋土挡墙土-筋相互作用机理[J]. 上海大学学报:自然科学版 , 2009, 15 (2) : 199-204 PENG Ming-yuan, HUANG Chao, PENG Ji-min, et al. Interaction between Soil and Inclusions in Retaining Wall Reinforced with Horizontal and Vertical Inclusions[J]. Journal of Shanghai University:Natural Science Edition , 2009, 15 (2) : 199-204 |
| [13] | 周淮, 张孟喜. 水平-竖向加筋土挡墙作用机理的离散元数值模拟[J]. 上海交通大学学报 , 2012, 46 (10) : 1548-1552 ZHOU Huai, ZHANG Meng-xi. Numerical Simulation on Mechanism of Soil Retaining Wall Reinforced with H-V Inclusions by DEM[J]. Journal of Shanghai Jiaotong University , 2012, 46 (10) : 1548-1552 |
| [14] | 张孟喜, 黄超. 刚性条带式带齿加筋土的极限拉拔力模型[J]. 岩土工程学报 , 2009, 31 (9) : 1336-1344 ZHANG Meng-xi, HUANG Chao. Ultimate Pullout Resistance Model for Rigid Denti-strip Reinforced Soil[J]. Chinese Journal of Geotechnical Engineering , 2009, 31 (9) : 1336-1344 |
 2017, Vol. 34
2017, Vol. 34
