扩展功能
文章信息
- 任俊达, 张怀志, 谭忆秋
- REN Jun-da, ZHANG Huai-zhi, TAN Yi-qiu
- 基于三维黏弹有限元法的沥青路面结构力学响应分析
- Analysis on Mechanical Response of Asphalt Pavement Structure Based on 3D Viscoelastic Finite Element Method
- 公路交通科技, 2017, 34(1): 15-23
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(1): 15-23
- 10.3969/j.issn.1002-0268.2017.01.003
-
文章历史
- 收稿日期: 2016-01-21
2. 哈尔滨工业大学 交通科学与工程学院, 黑龙江 哈尔滨 150090
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin Heilongjiang 150090, China
路面结构力学响应分析是解释路面病害及破坏机理的核心途径,而道路建筑材料的本构关系则是路面结构力学响应分析的重中之重[1]。由于沥青混合料是一种典型的黏弹性材料,有着与线弹性材料完全不同的本构关系, 对动态荷载作用下产生的力学响应有其特有的能量耗散规律[2]。然而,当前我国沥青路面分析与设计方法是基于多层弹性理论和静态响应分析的[3],在路面动态响应分析中将沥青混合料作为线弹性材料处理,这种简化处理方法不可避免地造成分析结果和路面结构实际行为的偏差;与此同时,由于路面结构表面的不平整性,在高速行车荷载作用下,车辆对路面施加的是典型的动态荷载[4],因此,只有对路面结构进行黏弹性动态分析,才能更客观地反映其行为特性。关于移动荷载下结构动力响应的研究将逐渐成为解决当前沥青路面复杂行为的切入点和着力点[5-8]。
关于沥青路面结构力学响应的分析国内外学者进行了大量的研究。邓学钧[9]等研究了黏弹性地基上的无限长梁在移动载荷作用下的响应。赵延庆[10-11]等利用三维黏弹性有限元模型模拟了移动荷载作用模式,分析了不同温度以及行车速度下沥青路面结构内部不同深度处的应力脉冲时间;同时分析了荷载模式及温度对典型沥青路面结构路表及沥青层底水平应力的影响。郭忠印[12]等研究了汽车在正常行驶与制动状态下沥青路面结构层竖向位移及剪应力的动态响应规律,解释了沥青路面在动载作用下的剪切破坏机理。Siddharthan等人[13-14]利用弹性力学原理,建立了移动荷载下层状体系动力学模型,探究了沥青路面材料的黏弹性质对路面结构力学响应的影响规律,在研究中,采用了更能体现沥青材料性质的复数剪切模量来代替传统的弹性模量;基于线性叠加原理,采用双层和三层黏弹性层状体系模型,研究了移动半正弦荷载作用下的动力响应。从上述研究现状可以看出,对于沥青路面黏弹性分析研究大多数仍停留在定性分析阶段。与此同时,上述诸多研究对于路面结构层材料参数的获取,大多采用假定的方法,缺少对材料性能参数的准确测定,其研究结果具有一定的局限性。尽管部分研究采用三维黏弹性有限元及动态荷载对路面结构力学响应进行了分析,但未进一步进行对应的现场试验从而验证模型及动力学响应的可靠性,其结论具有局限性,难以保证路面力学响应分析的准确性和可靠性。
因此,本文以辽宁省高速公路典型沥青路面结构为研究对象,针对传统算法的问题与不足,建立了完全基于实测参数的三维黏弹有限元仿真模型。采用动态模量试验方法,得到了典型沥青混合料的黏弹参数;利用FWD弯沉盆反算得到基层和土基的弹性模量;采用MLS 66加速加载试验系统模拟了车辆荷载的作用,并实测了轮胎接触面积分布。采用光纤光栅传感器,对足尺加速加载沥青路面进行了动力响应现场实测,通过计算值与实测值对比,对所建立的路面力学仿真模型进行验证。同时,对沥青路面结构内部的力学响应进行了分析。
1 路面结构模型建立 1.1 足尺加速加载试验路铺设按照辽宁省典型的高速公路沥青路面结构形式铺筑加速加载试验段,试验段结构如表 1所示。采用MLS 66加速加载试验系统,对路面进行加速加载试验,MLS 66具有自行移动功能,依靠直线感应电机可实现较高的加载频率,当达到设备的最大转速(6 000次/h)时,相当于22 km/h的行车速度。
| 材料类型 | 厚度/cm | 模量/MPa | 泊松比 |
| 上面层SMA-13 | 3.5 | 黏弹性 | 0.3 |
| 中面层AC-20 | 6 | 黏弹性 | 0.3 |
| 下面层AC-25 | 8 | 黏弹性 | 0.3 |
| 半刚性基层水泥稳定碎石 | 40 | 1 635.3 | 0.25 |
| 垫层级配砂砾 | 15 | 124.7 | 0.4 |
| 土基 | - | 124.7 | 0.4 |
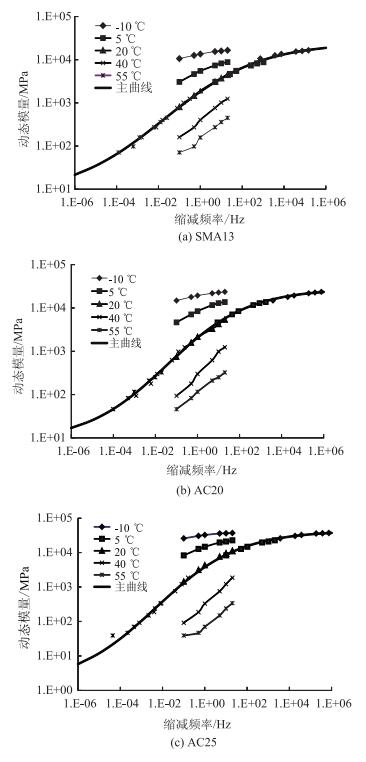
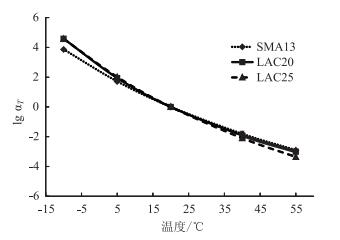
对于沥青混合料,利用动态模量试验得到黏弹力学参数[15],分别对SMA13,AC20,AC25混合料试件施加正弦荷载,测定其复数模量。根据时间-温度等效原理[12],确定了3种沥青混合料的动态模量主曲线(如图 1所示),同时得到各个温度下的时间-温度位移因子αT,如图 2所示。
|
| 图 1 动态模量主曲线 Fig. 1 Dynamic modulus master curve |
| |
|
| 图 2 时间-温度位移因子 Fig. 2 Time-temperature displacement factor |
| |
基层及土基弹性模量通过FWD弯沉盆反算得到。模量反算采用EVERCAL软件,采用三层反演体系,将水稳碎石和水稳砂砾作为一层(半刚性材料层),将垫层和土基作为一层。试验中得到半刚性材料模量的平均值为1 635.3 MPa,变异系数为11.2%;土基模量平均值为124.7 MPa,变异系数为12.7%。
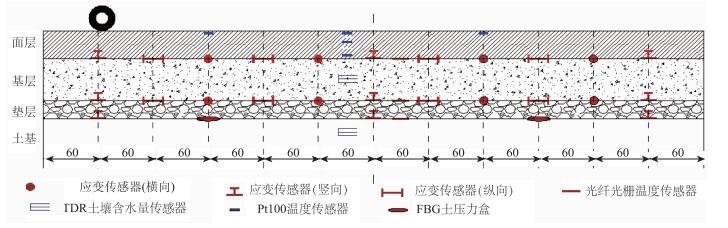
为能获取路面结构内部的力学响应,在加速加载试验路进行了光纤光栅应力应变传感器及环境参数传感器的现场埋设,对面层和基层底部竖向、横向、纵向三向应变及土基顶面压应力进行采集,同时实时采集路面结构内部温湿度状况。传感器沿加载段中心线布设,各层位传感器数量和位置如图 3所示。采用双轮荷载进行加载,轴载150 kN。加载位置包括正载和偏载两种方案,正载是指荷载单元两轮正中心位置位于传感器纵断面正上方;偏载是指荷载单元单轮中心位置位于传感器纵断面正上方。
|
| 图 3 加速加载试验段传感器布置图(单位:cm) Fig. 3 Layout of Sensors in accelerated loading test section (unit:cm) |
| |
1.2 三维黏弹有限元模型的建立
本研究基于大型有限元软件ABAQUS建立有限元分析模型。模型中假设各沥青混凝土层为均质、各向同性的黏弹性材料;水稳基层及土基为均质、各向同性的线弹性材料。由于虚位移原理的成立和本构关系无关,只需将弹性本构矩阵换为黏弹性本构矩阵即可。
通过对加载轮胎接地面积进行实测分析,每个轮胎接地面积由5块接地条纹组成,接地压力分别为0.69,0.86,0.9,0.86 MPa和0.69 MPa。由于结构和荷载的对称性,取1/2结构建立模型。对于本研究的问题,有限元模型必须足够大,才能保证得到路面结构内不同深度处完整的应力波形,并且当轮载在路面上移动时,可以消除边界条件的影响。通过试分析,确定有限元模型在长度、宽度和深度方向的尺寸分别为8.0,4.0 m和5.0 m。采用三维六面体八节点等参元,将路面结构划分为47 040个单元,共51 540个节点。各层层间状态为完全连续。除了对称边界条件外,底面和侧面均为法向完全约束。对于行车荷载的模拟参见文献[10]。
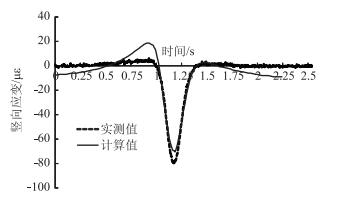
2 力学响应实测与计算比较分析 2.1 沥青层底实测与计算响应比较图 4为正载作用下沥青层底竖向应变随时间的变化规律。如图所示,计算值与实测值表现出了类似的变化趋势。当轮载从远处驶向分析点时,沥青层底承受较小的拉应变,此时计算的拉应变稍大于实测压应变;随着轮载进一步靠近,拉应变转向变为压应变,并逐渐到达峰值;而后当荷载驶离时,该点从受拉状态快速恢复至初始状态。从上述过程可以看出,路面在车辆驶过前后,经历了拉-压的交替变化,力学响应曲线呈现出显著的非对称性,且拉应变相对于压应变而言是不可忽略的。
|
| 图 4 正载作用下沥青层底竖向应变(5 km/h) Fig. 4 Vertical strain of asphalt layer bottom unde balanced loading (5 km/h) |
| |
图 5、图 6为偏载作用下沥青层底纵向应变和横向应变的实测值和计算值。可以看出,当轮载经过路面结构时,与压应变不同,沥青层底的水平应变会经过受压-受拉-再受压的变化过程。对于纵向应变,在轮载驶离过程中,计算的压应变大于实测值。对于横向应变,在轮载趋近过程中,实测压应变大于计算值。从整体上讲,计算结果同样可较好地模拟水平应变随时间的变化过程。
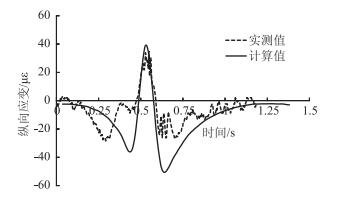
|
| 图 5 偏载作用下沥青层底纵向应变(10 km/h) Fig. 5 Longitudinal strain of asphalt layer bottom under unbalanced loading (10 km/h) |
| |
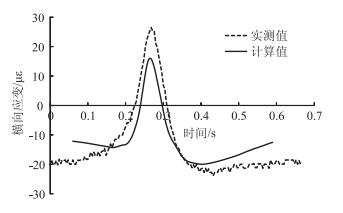
|
| 图 6 偏载作用下沥青层底横向应变(20 km/h) Fig. 6 Transverse strain of asphalt layer bottom under unbalanced loading (20 km/h) |
| |
2.2 半刚性材料层底实测与计算响应比较
图 7为水稳砂砾层底正载作用下纵向应变的实测值和计算值,可见在轮载趋近和驶离过程中,计算值和实测值很接近,力学响应曲线基本呈现对称性,响应持续时间较长,计算得到的水平拉应变的峰值较实测值稍小。图 8为水稳砂砾层底水平横向应变计算和实测的时程曲线,计算值和实测值同样吻合得很好。
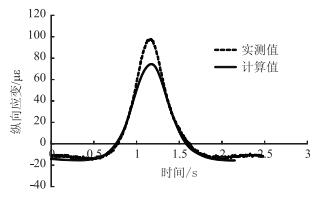
|
| 图 7 正载作用下水稳砂砾层底纵向应变(5 km/h) Fig. 7 Longitudinal strain of water-stabilized gravel layer bottom under balanced loading (5 km/h) |
| |
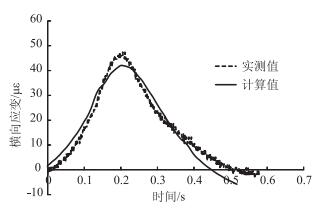
|
| 图 8 偏载作用下水稳砂砾层底横向应变(20 km/h) Fig. 8 Transverse strain of water-stabilized gravel layer bottomunder unbalanced loading (20 km/h) |
| |
2.3 土基顶面实测与计算响应比较
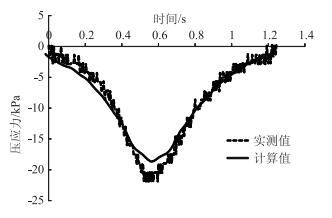
图 9为正载作用下土基顶面压应力的实测值和计算值。由图可知,计算值与实测值在不同荷载位置和形式速度下均非常接近,随着轮载趋近,路基顶面压应力开始出现并逐渐增大,加载和卸载阶段,其力学响应曲线呈对称状态,基本不受整体结构黏弹性影响。
|
| 图 9 正载作用下土基顶面压应力(10 km/h) Fig. 9 Compressive stress of soil base top under balanced loading (10 km/h) |
| |
由上述分析可以看出,所采用的建模方法和参数可以较好地模拟路面结构在移动轮载作用下不同工况路面结构内部的力学响应变化。在一些工况下,理论计算值和实测值存在局部的差异,这些差异来源于两个方面:一是实测数值和路面结构内真实力学响应的偏差;二是理论计算结果的误差。实测数据的误差取决于传感器的性能、精度、包装材料和传感器协同变形能力、传感器埋设位置等因素。
3 路面结构内部力学响应分析 3.1 竖向应力与应变分析由以上分析可知,利用三维黏弹性有限元可以较好地模拟现场移动轮载作用下路面结构内的力学响应。为探究沥青路面内部力学响应及变化规律,本节利用所建立的黏弹性三维有限元模型分别对路面结构层内部的竖向应力和应变、剪应力和剪应变、水平应力和应变进行分析。为便于比较,取响应-时间曲线的最大值进行分析,分析中取模型行车速度为45 km/h,温度为25 ℃。横向选取距轮隙中心不同距离的4处位置进行分析,即轮隙中心、轮内边缘、轮胎中心以及轮外边缘,分别分析各种力学响应在这4个横向位置下沿深度的变化情况。
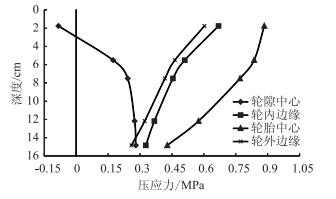
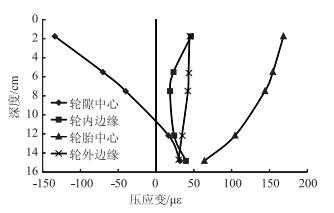
沥青层内竖向应力随深度变化如图 10、图 11所示,轮隙中心处的竖向应力、应变表现为随着深度增加拉应力、拉应变逐渐减小并变为压应力、压应变;且压应力、压应变随着深度的增加而增大,这是由于在轮隙中心靠近路表处路面结构向上弯曲造成的。轮外边缘以及轮胎中心处的压应力、压应变均随深度的增加而不断减小,其中轮胎中心在各个深度的压应力、压应变大小均明显高于同深度的其他位置,为不利位置。与此同时,在一定深度内,轮内边缘处压应力、压应变随深度的增加同样减小,与上述位置表现出相同的趋势,但在深度较大时,会出现压应变随深度的增加而增加的情况,这是由于轮内边缘靠近轮隙中心处,受路表向上弯曲影响而产生的。
|
| 图 10 沥青层内竖向压应力 Fig. 10 Vertical compressive stress of asphalt layer |
| |
|
| 图 11 沥青层内竖向压应变 Fig. 11 Vertical compressive strain of asphalt layer |
| |
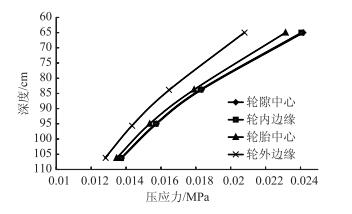
级配砂砾与土基竖向压应力、压应变随深度变化见图 12、图 13。由图可知,在级配砂砾与土基层内,距轮隙中心不同距离的各点竖向压应力、压应变均随深度的增加而减小,其中轮隙中心和轮内边缘在各个深度的压应力、压应变大小均高于同深度的其他位置。轮隙中心和轮内边缘比较数值发现,轮隙中心竖向压应力、压应变稍大于轮内边缘,为不利位置。
|
| 图 12 级配砂砾与土基竖向压应力 Fig. 12 Vertical compressive stress of graded gravel and soil base |
| |
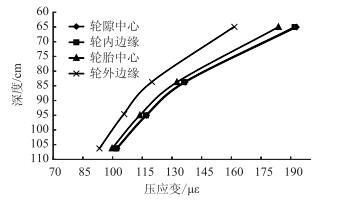
|
| 图 13 级配砂砾与土基竖向压应变 Fig. 13 Vertical compressive strain of graded gravel and soil base |
| |
3.2 剪应力与剪应变分析
在轮载作用下,其非均布荷载将在路面结构层内产生较大的剪应力,然而当前沥青混合料在设计过程中并未考虑材料的抗剪能力[16-18]。国内外学者曾对沥青路面的抗剪能力进行了研究,认为沥青混合料的永久变形主要是由于剪应力或剪应变引起的,并且粒料材料与土基的抗剪切性能也是重要影响因素。东南大学杨军[19]等通过三轴剪切试验发现,沥青混合料的抗剪强度与抗车辙性能之间有较好的关系,进一步说明了剪切疲劳是产生沥青路面车辙的主要原因之一。孙立军[20]等利用有限元分析ANSYS计算了沥青路面结构层内剪应力的分布规律,建立了剪应力分布规律曲线方程,并以此对路面车辙进行预估。Bekheet[21]等总结前人的研究成果认为:当基层强度足够的时候车辙主要产生于沥青面层,其机理为沥青混凝土的剪切变形。Paterson[22]研究认为一旦剪应力超过沥青混凝土的剪切强度或承受了足够的蠕变,车辙就会发生。因此,本文对沥青层、级配砂砾与土基内的剪应力和剪应变进行分析。
不同轮载作用位置下沥青层内的剪应力、剪应变分布如图 14和图 15所示。由图可知,剪应力和剪应变的分布规律基本一致。在沥青层内,轮隙中心处的剪应力和剪应变随深度的增加而降低,其他位置处的剪应力和剪应变沿深度方向先增大后减小。在横向位置,轮外边缘处各个深度的剪应力和剪应变较大,为不利位置。在深度方向,中面层和下面层上部剪应力和剪应变较大,所以应关注中、下面层,特别是中面层材料的抗车辙能力,对层间连续理想的三层式沥青面层,中面层通常是发生车辙变形的主要层位。
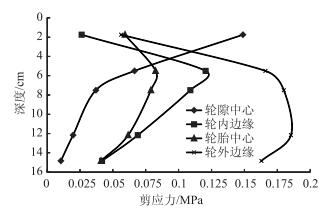
|
| 图 14 沥青层内剪应力 Fig. 14 Shear stress of asphalt layer |
| |
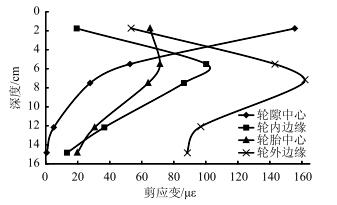
|
| 图 15 沥青层内剪应变 Fig. 15 Shear strain of asphalt layer |
| |
级配砂砾与土基内的剪应力和剪应变分布如图 16和图 17所示。由图可知,剪应力和剪应变的分布规律基本一致。在级配砂砾与土基层内,不同位置处的剪应力和剪应变均随深度的增加而减小,其中轮外边缘处在各个深度的剪应力和剪应变均大于同深度的其他位置,此规律与沥青层相符,均为不利位置。
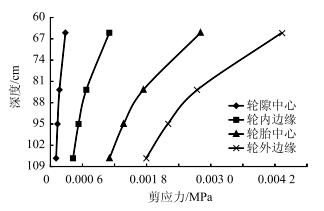
|
| 图 16 级配砂砾与土基层内剪应力 Fig. 16 Shear stress of graded gravel and soil base |
| |
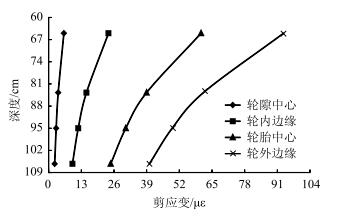
|
| 图 17 级配砂砾与土基层内剪应变 Fig. 17 Shear strain of graded gravel and soil base |
| |
3.3 水平拉应力与拉应变分析
行车荷载在路面结构内产生的水平拉应力、拉应变主要用来评价路面结构的疲劳开裂性能,水平拉应力、拉应变包括纵向和横向的拉应力和拉应变。与分析永久变形时相关的力学响应不同,对于疲劳开裂而言,与其力学响应密切相关的关键位置在各结构层的底部,所以本课题中分别分析了沥青层底、水泥稳定碎石层底的水平拉应力和拉应变。由于结构和荷载形式具有对称性,而轮隙中心位于对称面上,所以不用分析轮隙中心的横向应力、应变值。
图 18和图 19分别为沥青层底水平拉应力和拉应变的计算结果。由图可知,水平拉应变和水平拉应力表现出相似的分布规律。在沥青层底,不同位置处沿水平纵向均受到拉应力、拉应变作用,其中轮隙中心与轮胎中心纵向拉应力、拉应变均较大,为不利位置。在轮内边缘处,沥青层底在横向受较小的压应力和压应变作用,其他位置处则受横向拉应力和拉应变的作用。比较纵向和横向的力学响应,可知纵向的拉应力和拉应变要远大于横向的相应力学响应,所以控制沥青层疲劳开裂的力学响应是纵向拉应力或拉应变。
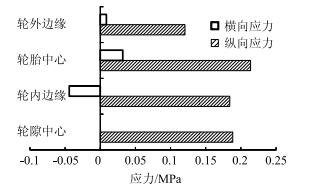
|
| 图 18 沥青层底水平拉应力 Fig. 18 Horizontal tensile stress of asphalt layer bottom |
| |
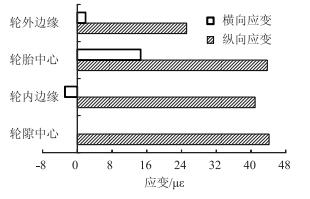
|
| 图 19 沥青层底水平拉应变 Fig. 19 Horizontal tensile strain of asphalt layer bottom |
| |
图 20和图 21为水泥稳定碎石层底水平拉应力和拉应变的结果。由图可知,水泥稳定碎石层底水平拉应变和水平拉应力表现出相似的分布规律。不同位置处沿水平纵向和横向均受到拉应力、拉应变作用,其中轮隙中心、轮内边缘、轮胎中心处纵向拉应力、应变相互差距不大;而轮外边缘的拉应力、应变则较小。比较横向和纵向的力学响应可知,水稳碎石层底的纵向拉应力和拉应变明显大于横向的力学响应,所以控制水稳碎石层疲劳开裂的力学响应是纵向拉应力或拉应变。
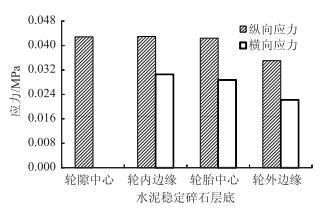
|
| 图 20 水泥稳定碎石层底水平拉应力 Fig. 20 Horizontal tensile stress of cement stabilized macadam bottom |
| |
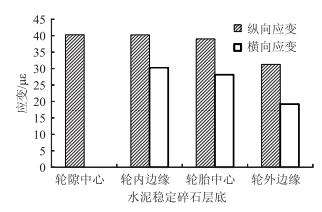
|
| 图 21 水泥稳定碎石层底水平拉应变 Fig. 21 Horizontal tensile strain of cement stabilized macadam bottom |
| |
4 结论
本文基于辽宁省沥青路面足尺加速加载试验,排除了假定参数的影响,建立了基于实测参数的路面结构三维黏弹性有限元分析模型,通过对轮隙中心、轮内边缘、轮胎中心以及轮外边缘位置处力学响应进行研究,得到以下有效结论:
(1)计算值和实测值表明:在行车荷载作用下,沥青层底竖向受力呈现拉压交替变化;沥青层底水平受力为压-拉-压变化;半刚性基层层底以受拉为主;土基顶面承受压力作用。由于荷载随深度扩散,随着结构深度的增加,力学响应曲线的持续时间增加。沥青混合料黏弹特性导致的弹性后效使得沥青层的力学响应呈现非对称分布特点,而基层和路基处于弹性状态,其力学响应曲线呈现对称分布状态。
(2)在沥青层内,轮隙中心处竖向应力、应变随着深度增加由受拉状态变为受压状态,并逐渐增大。其余位置的压应力、压应变随着深度的增加而不断减小,由于路面弯曲的影响,当深度较大时,轮内边缘处压应变会随着深度的增加而增加。对于粒料层,4个位置的力学响应均表现为受压状态,且压应力、压应变随着深度的增加而减小。沥青层中竖向压应力和压应变的不利位置为轮胎中心,对于粒料层不利位置为轮隙中心。
(3)通过对路面结构的剪应力和剪应变分析表明:在沥青层内,轮隙中心处的剪应力和剪应变随深度的增加而降低,其他位置处的剪应力和剪应变沿深度方向先增大后减小;轮外边缘处为剪应力和剪应变的不利位置;在深度方向,中面层和下面层上部剪应力和剪应变较大,为车辙发生的薄弱部位。对于粒料层,不同位置处的剪应力和剪应变均随深度的增加而减小,轮外边缘处仍为不利位置。
(4)通过对行车荷载作用下路面结构内水平拉应力、拉应变分析发现:对于沥青层底、水泥稳定碎石层底,控制疲劳开裂的力学响应为水平纵向拉应力和拉应变,不利位置分别为轮隙中心和轮胎中心的相应层底处。
| [1] | 赵延庆, 刘慧, 白龙, 等. 沥青混合料本构关系对路面力学响应的影响[J]. 中国公路学报 , 2012, 25 (5) : 6-11 ZHAO Yan-qing, LIU Hui, BAI Long, et al. Effect of Constitutive Relationship of Asphalt Mixture on Pavement Response[J]. China Journal of Highway and Transport , 2012, 25 (5) : 6-11 |
| [2] | 赵延庆, 谭忆秋, 王国忠, 等. 黏弹性对沥青路面疲劳开裂的影响[J]. 吉林大学学报:工学版 , 2010, 40 (3) : 683-687 ZHAO Yan-qing, TAN Yi-qiu, WANG Guo-zhong, et al. Effect of Viscoelasticity on Fatigue Cracking of Asphalt Pavement[J]. Journal of Jilin University:Engineering and Technology Edition , 2010, 40 (3) : 683-687 |
| [3] | 侯芸, 郭忠印, 田波, 等. 动荷作用下沥青路面结构的变形响应分析[J]. 中国公路学报 , 2002, 15 (3) : 6-10 HOU Yun, GUO Zhong-yin, TIAN Bo, et al. Dynamic Deflection Response of Layered Pavement Structure Subjected to Dynamic Load[J]. China Journal of Highway and Transport , 2002, 15 (3) : 6-10 |
| [4] | 董忠红, 吕彭民. 移动荷载下粘弹性层状沥青路面动力响应模型[J]. 工程力学 , 2011, 28 (12) : 153-159 DONG Zhong-hong, LÜ Peng-min. A Model to Study the Dynamic Response of Visco-elastic Layered System under Moving Load[J]. Engineering Mechanics , 2011, 28 (12) : 153-159 |
| [5] | 董泽蛟, 曹丽萍, 谭忆秋, 等. 移动荷载作用下沥青路面三向应变动力响应模拟分析[J]. 土木工程学报 , 2009, 42 (4) : 133-139 DONG Ze-jiao, CAO Li-ping, TAN Yi-qiu, et al. Analysis of the Dynamic Response of Three Directional Strains in Asphalt Pavement Under Moving Vehicle Loads[J]. China Civil Engineering Journal , 2009, 42 (4) : 133-139 |
| [6] | WU C P, SHEN P A. Dynamic Analysis of Concrete Pavements Subjected to Moving Loads[J]. Journal of Transportation Engineering , 1996, 122 (5) : 367-373 |
| [7] | SAAD B, MITRI H, POOROOSHASB H. Three-dimensional Dynamic Analysis of Flexible Conventional Pavement Foundation[J]. Journal of Transportation Engineering , 2005, 131 (6) : 460-469 |
| [8] | DONG Z J, CAO L P, TAN Y Q. Numerical Response Analysis and Experimental Simulation of Saturated Asphalt Pavement Under Dynamic Vehicle Loading[C]//Symposium of Pavement Mechanics and Materials. Blacksburg:ASCE, 2007:1-13. |
| [9] | 孙璐, 邓学钧. 运动负荷下粘弹性Kelvin地基上无限大阪的稳态响应[J]. 岩土工程学报 , 1997, 19 (2) : 17-25 SUN Lu, DENG Xue-jun. Steady Response of Infinite Plate on Viscoelastic Kelvin Foundation to Moving Load[J]. Chinese Journal of Geotechnical Engineering , 1997, 19 (2) : 17-25 |
| [10] | 赵延庆, 王志超, 王国忠, 等. 移动荷载下沥青路面内应力脉冲的持续时间[J]. 交通运输工程学报 , 2009, 9 (6) : 11-15 ZHAO Yan-qing, WANG Zhi-chao, WANG Guo-zhong, et al. Stress Pulse Durations in Asphalt Pavement under Moving Load[J]. Journal of Traffic and Transportation Engineering , 2009, 9 (6) : 11-15 |
| [11] | 赵延庆, 周长红, 王国忠, 等. 脉冲荷载下沥青路面粘弹性响应分析[J]. 大连理工大学学报 , 2011, 51 (1) : 73-77 ZHAO Yan-qing, ZHOU Chang-hong, WANG Guo-zhong, et al. Analyses of Viscoelastic Responses of Asphalt Pavements under Pulse Loading[J]. Journal of Dalian University of Technology , 2011, 51 (1) : 73-77 |
| [12] | 马新, 郭忠印, 李志强, 等. 动载作用下沥青路面的剪切破坏机理[J]. 中国公路学报 , 2009, 22 (6) : 34-39 MA Xin, GUO Zhong-yin, LI Zhi-qiang, et al. Shear Destruction Mechanism of Asphalt Pavement under Moving Load[J]. China Journal of Highway and Transport , 2009, 22 (6) : 34-39 |
| [13] | SIDDHARTHAN R V, KRISHNAMENON N, SEBAALY P E. Finite-layer Approach to Pavement Response Evaluation[J]. Transportation Research Record , 2000, 1709 : 43-49 |
| [14] | SIDDHARTHAN R V, SEBAALY P E, EL-DESOUKY M, et al. Heavy Off-road Vehicle Tire-pavement Interactions and Response[J]. Journal of Transportation Engineering , 2005, 131 (3) : 239-247 |
| [15] | 迟凤霞, 张肖宁, 王丽健, 等. 沥青混合料动态剪切模量主曲线的确定[J]. 吉林大学学报:工学版 , 2009, 39 (2) : 349-353 CHI Feng-xia, ZHANG Xiao-ning, WANG Li-jian, et al. Determination of Master Curve of Dynamic Shearing Modulus of Asphalt Mixture[J]. Journal of Jilin University:Engineering and Technology Edition , 2009, 39 (2) : 349-353 |
| [16] | 林绣贤. 关于沥青混凝土路面设计中抗剪指标的建议[J]. 公路 , 2005 (12) : 66-69 LIN Xiu-xian. Recommendations for Shear Resistant Criteria in Asphalt Concrete Pavement Design[J]. Highway , 2005 (12) : 66-69 |
| [17] | 陈小庭, 孙立军, 李峰. 长寿命沥青混凝土路面结构特点与设计研究[J]. 公路 , 2005 (8) : 239-243 CHEN Xiao-ting, SUN Li-jun, LI Feng. Structural Characters of Perpetual Asphalt Concrete Pavements and Design[J]. Highway , 2005 (8) : 239-243 |
| [18] | 高燕希, 曾红雄, 张东省. 沥青混合料抗剪强度影响因素研究[J]. 公路交通科技 , 2009, 26 (8) : 28-32 GAO Yan-xi, ZENG Hong-xiong, ZHANG Dong-sheng. Research on Influencing Factors on Asphalt Mixture Shear Strength[J]. Journal of Highway and Transportation Research and Development , 2009, 26 (8) : 28-32 |
| [19] | 朱浩然, 杨军, 陈志伟. 沥青混合料抗剪性能的三轴剪切试验[J]. 交通运输工程学报 , 2009, 9 (3) : 19-23 ZHU Hao-ran, YANG Jun, CHEN Zhi-wei. Triaxial Shear Test on Anti-shear Properties of Asphalt Mixture[J]. Journal of Traffic and Transportation Engineering , 2009, 9 (3) : 19-23 |
| [20] | 许严, 孙立军. 沥青路面沥青层剪应力变化简化模型研究[J]. 同济大学学报:自然科学版 , 2012, 40 (2) : 211-216 XU Yan, SUN Li-jun. Research on Simplified Model for Variation of Shear Stress of Asphalt Layers in Asphalt Pavements[J]. Journal of Tongji University:Natural Science Edition , 2012, 40 (2) : 211-216 |
| [21] | BEKHEET W. Investigations of In-situ Shear Properties of Asphalt Pavement[D]. Ottawa:Carleton University, 2002. |
| [22] | PATERSON W D O. Road Deterioration and Maintenance Effect:Models for Planning and Management, the Highway Design and Maintenance Standard Series[M]. Baltimore: Johns Hopkins University Press, 1987 . |
 2017, Vol. 34
2017, Vol. 34
