扩展功能
文章信息
- 赖元文, 苏荣霖, 薛建州
- LAI Yuan-wen, SU Rong-lin, XUE Jian-zhou
- 交叉口设置导流岛的信号控制临界条件研究
- Study on Signal Control Critical Condition for Setting Channelized Islands at Intersection
- 公路交通科技, 2016, 33(12): 125-129
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(12): 125-129
- 10.3969/j.issn.1002-0268.2016.12.020
-
文章历史
- 收稿日期: 2016-03-11
信号交叉口交通的组织优化是提高交叉口交通安全和通行能力的重要手段,交通组织优化关键是如何分配好交叉口有限的时空资源,在交叉口设置导流岛是重要的方式之一。对于交通流量大的交叉口,光靠空间上的渠化还不能解决问题,还需从时间上把交通流量分离开。国内外学者对信号控制与交叉口设计的协调已有不少研究成果。Perez[1]提出在交叉口设计过程中充分考虑设置右转渠化设施,制订了旨在减少延误的右转设计准则,建议采用保护型左转相位阶段让车辆右转,这样可以减少延误,但没有提出量化指标。Tarawneh等[2]研究了信号交叉口红灯右转的几何条件对驾驶员的影响,为信号交叉口的设计提供了依据。Roefaro[3]分析了右转渠化后对交通安全的影响,研究了驾驶员对右转渠化设施的反应,并对右转渠化后信号控制提出了相应的建议。Macfarlane等[4]研究了右转渠化信号交叉口的右转车辆延误与驾驶员犹豫时间的关系,建议在设计过程中给驾驶员足够的指示信息。马建明等[5]从信号配时的基本参数、交通口交通工程措施及交通管理措施等方面对交叉口的交通组织进行了优化。王殿海等[6]研究了在左转车辆到达率相对稳定的情况下,设置左弯待转区的左转相位信号配时的临界条件。李丽丽等[7]建立了可变导向车道功能和相位有效绿灯时间为决策变量的预设信号配时优化模型,得出可变导向车道功能和相位有效绿灯时间存在最佳组合。王京元等[8]基于排队理论,建立了保护相位下左转车道的存储长度计算模型。张碧琴等[9]分析了新建城区交叉口行人与右转机动车的冲突,建模分析了信号周期内行人与右转车辆分相位设置的临界状态。刘应东等[10]提出了短连线交叉口元胞自动机交通流模型,得出短连线交叉口的交通流量与连线长度、信号周期和相位差相关。目前针对交叉口设置导流岛的信号控制临界条件还没有专门的研究,本文采用交通波理论研究在交叉口设置导流岛的行人和自行车过街信号临界条件、机动车信号临界条件及机非信号相位和配时的协调方法。
1 行人和自行车过街信号临界条件以典型的四相位信号控制为例,左转行人和自行车过街采用二次过街方式,信号相位和配时如图 1所示。导流岛中等待过街的行人和自行车分别往两个方向过街。
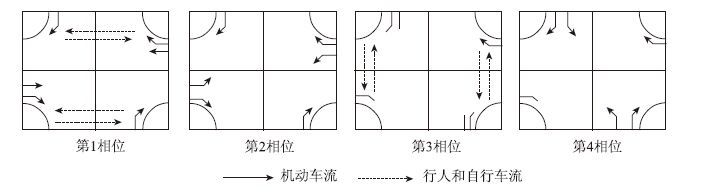
|
| 图 1 交叉口行人和自行车过街信号相位和配时 Fig. 1 Phase and timing scenarios for pedestrians and bicycles crossing street at intersection |
| |
表 1描述了典型四相位信号控制交叉口等待过街的行人和自行车的累积情况,如果在相位末有滞留量,那么导流岛中累积的行人和自行车将越来越多,这将导致行人和自行车溢出导流岛而在右转车道排队等待,严重影响车辆右转。因此,对于已有的设置导流岛的交叉口,需要进行合理的信号配时。
| 时间点 | 东南角及西南角导流岛往北方向、西北角及东北角导流岛往南方向行人和自行车 | 东南角及东北角导流岛往西方向、西南角及西北角导流岛往东方向行人和自行车 |
| 第1相位末 | 累积了第4、第1相位到达量及第3相位释放滞留量 | 累积了第1相位释放滞留量 |
| 第2相位末 | 累积了第4、第1、第2相位到达量及第3相位滞留量 | 累积了第2相位到达量及第1相位滞留量 |
| 第3相位末 | 累积了第3相位滞留量 | 累积了第2、第3相位到达量及第一相位滞留量 |
| 第4相位末 | 累积了第4相位到达量及第3相位滞留量 | 累积了第2、第3、第4相位到达量及第1相位滞留量 |
1.1 最短绿灯时间
设置导流岛后,行人、自行车过街相位绿灯时间可由行人和自行车离开导流岛的时间、过街所需时间和绿闪时长来确定,因此行人、自行车过街相位的绿灯时间为:
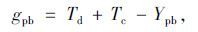
|
(1) |
式中,gpb为行人、自行车过街相位的绿灯时长;Td为排队等待的行人、自行车释放时间;Tc为行人、自行车穿越人行横道时间;Ypb为行人、自行车过街相位绿闪时长。
(1) 释放时间计算
我国信号交叉口行人和自行车混行比较常见,为了分析方便,首先需对行人、自行车进行换算。行人、自行车过街占用的时空资源应与过街占用面积成正比,而与过街速度成反比[11]。因此,可认为自行车相对于行人的换算系数为:
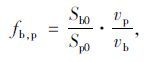
|
(2) |
式中,fb,p为自行车相对于行人的换算系数;Sp0为行人占用面积;Sb0为自行车占用面积;vp为行人过街速度;vb为自行车过街速度。
假设各进口单位时间内到达导流岛往同一方向的行人、自行车数量符合泊松分布,且不受上游交叉口信号控制的影响。将行人、自行车的到达率转换为以行人为单位的到达率,那么导流岛的行人、自行车混合到达率为:
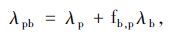
|
(3) |
式中,λpb为各进口同方向的行人、自行车混合到达率;λp为各进口同方向的行人到达率;λb为各进口同方向的自行车到达率。
绿灯亮时,行人、自行车进入人行横道过街,利用交通波理论[12]计算单位时间内的释放量:
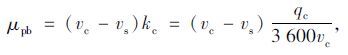
|
(4) |
式中,μpb为单位时间内的释放量;vc为过街速度;vs为启动速度;kc为人行横道混合流密度;qc为人行横道混合流量。
在绿灯亮起后,释放的行人、自行车交通量由两部分组成:一部分是在过街相位红灯期间累积的交通量,另一部分是在释放期间到达的行人和自行车。为了使行人、自行车在绿灯相位末不滞留,这两部分行人和自行车都必须在释放期间全部释放,其临界条件为:
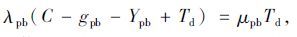
|
(5) |
式中,C为信号周期时长;gpb为行人、自行车过街相位的绿灯时长;Ypb为行人、自行车过街相位的绿闪时长。
由式(5)可得,排队等待的行人、自行车释放时间为:
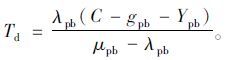
|
(6) |
(2) 穿越时间计算
行人、自行车穿越人行横道的时间通常采用人行横道长度与过街速度的比值,为了确保行人安全过街,以行人过街速度来计算穿越时间。
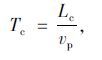
|
(7) |
式中,Lc为人行横道长度;vp为行人过街速度。
将式(6)、式(7)代入式(1)可得:
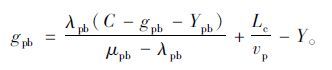
|
(8) |
通过变换式(8)可得设置导流岛信号交叉口行人、自行车过街相位的最短绿灯时长为:
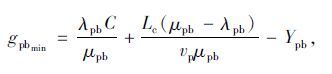
|
(9) |
式中,gpbmin为行人、自行车过街相位的最短绿灯时长。
1.2 最长红灯时间红灯期间到达的行人和自行车都在导流岛排队等待过街,此时到达的行人、自行车所占用的面积分别为:
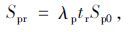
|
(10) |
式中,Spr为红灯期间到达行人所占用面积;tr为行人、自行车过街相位的红灯时长。
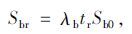
|
(11) |
式中Sbr为红灯期间到达自行车所占用的面积。
为了使排队等待的行人和自行车不发生溢出,行人、自行车占用的面积不能超过导流岛面积,因此有:
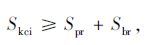
|
(12) |
式中Skci为导流岛面积。
将式(10)、式(11)代入式(12),可得行人、自行车过街相位的最长红灯时长为:
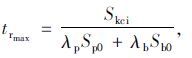
|
(13) |
式中,trmax为行人、自行车过街相位的最长红灯时长。
1.3 绿灯间隔时间(1) 与上一相位的绿灯间隔时间
如图 2所示,南北方向行人和自行车过街绿灯相位与上一左转相位存在以下潜在冲突:行人、自行车过街相位绿灯初期驶出导流岛,与上一左转相位绿灯末期驶出停车线的左转尾车在冲突点A处或B处的冲突。为避免出现冲突,相位之间应设置绿灯间隔时间,因此,南进口、北进口直行相位与上一相位即东进口、西进口左转相位需设置绿灯间隔时间。
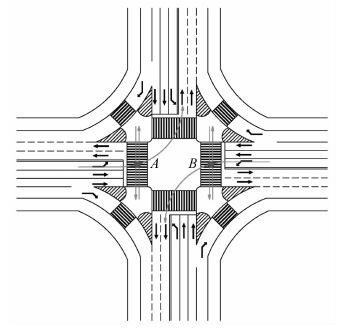
|
| 图 2 行人和自行车绿灯初期可能出现的冲突 Fig. 2 Possible conflict of pedestrians and bicycles at early green time |
| |
为了避免A处或B处机非冲突的发生,需满足以下条件:
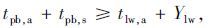
|
(14) |
式中,tpb,a为最快的行人或自行车从导流岛到达冲突点A或B的时间;tpb,s为安全间隔时间;tlw,a为上一左转相位左转尾车从停车线驶出到冲突点A或B的时间;Ylw为行人、自行车过街相位与上一左转相位的绿灯间隔时间。
(2) 与下一相位的绿灯间隔时间
如图 3所示,南北方向行人和自行车过街绿灯相位与下一左转相位存在潜在冲突点C或D的冲突。
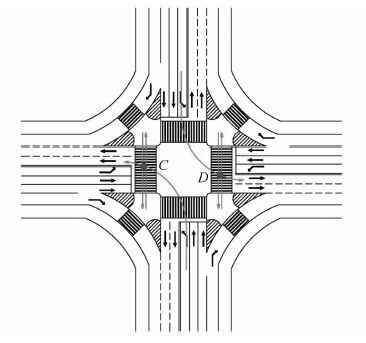
|
| 图 3 行人和自行车绿灯末期可能出现的冲突 Fig. 3 Possible conflict of pedestrians and bicycles at end green time |
| |
为了避免C处或D处机非冲突的发生,需满足以下条件:
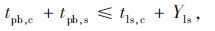
|
(15) |
式中,tpb,c为相位末最后的行人或自行车从导流岛到达冲突点C或D的时间;tls,c为下一左转相位左转车辆从停车线驶出到冲突点C或D的时间;Yls为行人、自行车过街相位与下一左转相位的绿灯间隔时间。
2 机动车信号临界条件设置导流岛前后左转信号配时不变,对信号配时的影响主要体现在直行相位,而与直行相位直接相关的是直右共用车道的阻塞。考虑到设置导流岛的信号交叉口在进口道都有拓宽渠化,设置短右转车道较为常见。
采用VISSIM软件对信号交叉口进行仿真,仿真采用的数据为:信号交叉口右转车道长度为120 m,直右共用车道车辆到达流率为650 pcu/h,其中右转车辆比例为50%。仿真时设置的信号周期时长分别为80,100,120 s,变化直行绿灯时间,得出共用车道发生阻塞的概率,结果如图 4所示。
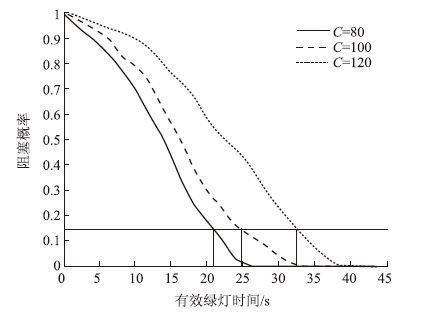
|
| 图 4 信号配时与阻塞概率关系图 Fig. 4 Relation between signal timing scenario and blocking probability |
| |
阻塞发生的概率与直行相位绿灯时间相关,为了避免阻塞造成的通行能力下降及延误增加,可以按照15%位阻塞概率对应的直行绿灯作为下限值。从图 4可见,有效信号周期时长为80,100,120 s时,15%阻塞概率对应的直行绿灯时间分别为21,25,32 s作为最小直行绿灯时间。
3 机非信号相位和配时的协调在信号配时的过程中,通常是根据行人、自行车交通量和机动车各转向交通量进行配时。同时,需要考虑行人、自行车过街信号临界条件与机动车信号临界条件的协调。如行人、自行车过街绿灯相位与机动车直行共用相位,那么最小绿灯时长应采用:
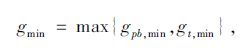
|
(16) |
式中,gmin为行人、自行车过街与直行机动车共用相位最小绿灯时长;gpb,min为行人、自行车过街相位最小绿灯时长;gt,min为直行相位最小绿灯时长。
4 结论在信号交叉口设置导流岛是常用的渠化方式,本文从信号控制角度对设置导流岛的临界条件进行了讨论。以交通波理论为基础,分析了行人和自行车过街信号的最小绿灯时长、最长红灯时长和绿灯间隔时间的阈值。采用仿真方法给出了不同周期时长下直行机动车最短绿灯时间的阈值。设置导流岛的信号控制临界条件研究结果表明,行人和自行车最短绿灯时间与释放时间、过街时间和绿闪时间相关,最长红灯时长应保证红灯期间到达导流岛的行人和自行车不溢出导流岛,绿灯间隔时间需避免冲突的发生。应用交通波理论进行了建模分析,给出了特定信号周期时长条件下的机动车直行最小绿灯时间。
| [1] | PEREZ R A. Guidelines for Right-turn Treatments at Signalized Intersections[J]. ITE Journal , 1995, 65 (2) : 23-27 |
| [2] | TARAWNEH M S, MCCOY P T. Effect of Intersection Channelization and Skew on Driver Performance[J]. Transportation Research Record , 1996, 1523 : 73-82 |
| [3] | ROEFARO S A. Channelized Right-turning Lanes at Signalized Intersections:A Review of Practice and an Empirical Study[D]. Bozeman:Montana State University, 2011. http://cn.bing.com/academic/profile?id=157953164&encoded=0&v=paper_preview&mkt=zh-cn |
| [4] | MACFARLANE G S, SAITO M, SCHULTZ G G. Delay Underestimation at Free Right-turn Channelized Intersections[J]. Procedia-Social and Behavioral Sciences , 2011, 16 (1) : 560-567 |
| [5] | 马建明, 张海涛, 任福田, 等. 信号交叉口交通组织与管理方案优化分析系统设计[J]. 公路交通科技 , 2001, 18 (5) : 87-89 MA Jian-ming, ZHANG Hai-tao, REN Fu-tian, et al. Study on Optimizing Traffic Operation of Signalized Intersection[J]. Journal of Highway and Transportation Research and Development , 2001, 18 (5) : 87-89 |
| [6] | 王殿海, 李丽丽, 陈永恒. 机动车左弯待转区设置的临界条件[J]. 公路交通科技 , 2009, 26 (11) : 132-135 WANG Dian-hai, LI Li-li, CHEN Yong-heng. Critical Condition for Setting Left-turn Waiting Area[J]. Journal of Highway and Transportation Research and Development , 2009, 26 (11) : 132-135 |
| [7] | 李丽丽, 姚荣涵, 周红媚, 等. 渠化可变导向车道交叉口预设信号配时优化模型[J]. 吉林大学学报:工学版 , 2015, 45 (1) : 75-81 LI Li-li, YAO Rong-han, ZHOU Hong-mei, et al. Optimization Model for Pretimed Signals at an Intersection with Reversible Approach Lanes[J]. Journal of Jilin University:Engineering and Technology Edition , 2015, 45 (1) : 75-81 |
| [8] | 王京元, 王炜. 保护相位下左转车道存储段长度计算[J]. 东南大学学报:自然科学版 , 2010, 40 (4) : 852-859 WANG Jing-yuan, WANG Wei. Calculation of Storage Lengths for Left-turn Lanes with Protected Phases[J]. Journal of Southeast University:Natural Science Edition , 2010, 40 (4) : 852-859 |
| [9] | 张碧琴, 高佳. 新建城区交叉口右转机动车与行人分相位设置临界研究[J]. 中国公路学报 , 2010, 23 (2) : 99-104 ZHANG Bi-qin, GAO Jia. Research on Critical State of Sub-phase Setting between Right-turn Motor Vehicles and Pedestrians for New Urban Zone Intersections[J]. China Journal of Highway and Transport , 2010, 23 (2) : 99-104 |
| [10] | 刘应东, 牛惠民, 王建强. 短连线信号交叉口的元胞自动机模型[J]. 公路交通科技 , 2015, 32 (2) : 140-146 LIU Ying-dong, NIU Hui-min, WANG Jian-qiang. Cellular Automata Model of Short-link Grouped Intersections[J]. Journal of Highway and Transportation Research and Development , 2015, 32 (2) : 140-146 |
| [11] | 李文勇, 陈学武, 王庆, 等. 路段人行横道通行能力及过街绿灯时间计算[J]. 武汉理工大学学报:交通科学与工程版 , 2006, 30 (5) : 751-754 LI Wen-yong, CHEN Xue-wu, WANG Qing, et al. Algorithm of Mid-block Street Crossing Capacity and Cross-street Green Time[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering , 2006, 30 (5) : 751-754 |
| [12] | DAVID L G, MATTHEW J H. Traffic Flow Theory[M]. Washington, D.C.: Transportation Research Board, 1976 . |
 2016, Vol. 33
2016, Vol. 33
