扩展功能
文章信息
- 江志彬, 谷金晶
- JIANG Zhi-bin, GU Jin-jing
- 基于公交线网布局的区域时刻表编制
- Compilation of Regional Timetable Based on Transit Network Layout
- 公路交通科技, 2016, 33(12): 113-117
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(12): 113-117
- 10.3969/j.issn.1002-0268.2016.12.018
-
文章历史
- 收稿日期: 2016-04-25
2. 同济大学 道路与交通工程教育部重点实验室, 上海 201804
2. Key Lab of Road and Traffic Engineering of Ministry of Education, Tongji University, Shanghai 201804, China
公交线网系统既是公交供给能力的基础硬件环境,又是诱发公交客流集散的载体。路网布局形态由线路间的交叉点个数及位置决定,它影响着路网中各换乘站客流量大小、乘客出行时间及方便程度,继而影响整个线网的运营效率。乘客出行总时间又是制订时刻表方案时需要考虑的重要因素。可见,公交运营中线网布局形态与时刻表编制的相关性不能被弱化。
时刻表编制问题中已有一些学者考虑了公交线路布局。Salzborn[1]和Shrivastava[2]研究了多条支线与1条主干线相连时,所需车辆数最小的时刻表编制问题。Hall[3]分析了1组支线与主干线在单一公交站点处交叉时,运行时间服从随机延迟分布情况下的时刻表优化。Abkowite[4]研究了两条交叉公交线路的时刻表编制情况。Maxwell[5]和Zhao[6]研究了干线与支线的同步换乘策略。司徒炳强[7]研究了存在合作与竞争关系线路的到站时间差问题,并采用启发式算法求解了时刻表模型。陈霞[8]基于公交线网结构提出了换乘站点权重系数,继而建立时刻表模型,采用遗传算法进行了有效性检验。
现有研究仅针对局部单一的衔接模式进行研究,但对整个公交线网没有系统研究。时刻表模型多集中考虑车辆同时到达,对线路间关系的划分不明确。因此,本文以线路衔接处的换乘站点为切入点,统筹考虑公交线网衔接模式与运营时刻表,以期达到扩大研究应用范围和提高公交运行效率的目的。
1 线网布局与区域时刻表作用机理 1.1 公交线网衔接模式公交线网衔接模式和线路关系的差异导致了不同的线路布局形式。对实际公交线网中的线路关系和衔接形式进行提炼,如表 1所示。
| 线路关系 | 衔接形式 | 描述 | 图示 |
| 组合关系 | 串联 | 不同线路布设于同一条城市道路上,但其服务和运送的客流有较大差别,适宜公交线路间的组合接驳,利于客流换乘 |  |
| 并联 | 分别布设于平行道路上,公交主干线并联,可满足主要交通走廊的客流需求,干线公交和支线公交并联,满足了居民不同出行要求 |  | |
| 层级关系 | 叉联 | 公交线路呈交叉形式,一般在交叉点处设置公交换乘点,以满足线路间客流换乘需求,是最常见的公交线路连接形式 |  |
| 枝联 | 是公交集散线路与骨架线路之间的一种连接方式,其关系形似枝叶,集散线路多以环线形式汇集和疏散集散点周边客流 |  |
串并联形式衔接的大站快线与干线公交线路组合运营,既可增加公交系统运送乘客的能力,又为乘客提供更好的服务。叉联和枝联的支线公交和社区公交线路相互配合,在提高换乘效率的同时,可将大站快车与干线公交的服务延伸到外围的周边地区。具有多层级线网服务功能,线路运送速度分级分离和分级集散换乘的运营优势。
1.2 线网布局与时刻表编制作用机理线网衔接模式对公交出行时间的影响表现在:大站快车与干线公交组合运营,主要考虑乘客候车时间和在车时间。层级间公交区域协调运营主要考虑乘客换乘时间和候车时间。可通过发车间隔和发车时刻来表征线网衔接模式对时刻表编制的影响机理。
(1) 发车间隔
组合关系线路发车间隔的设置,影响串联线路上乘客的候车时间和换乘等车时间。乘客依据自身出行需求,对不同发车间隔的并联线路会进行选择和区分。发车间隔直接影响层级间线路在换乘点处的换乘等待时间。
(2) 发车时刻
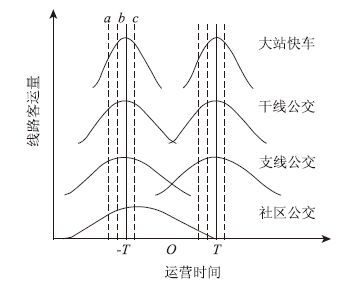
公交站点是关联线路的最重要节点,车辆到站时间影响乘客的候车时间和换乘时间。本文根据线路间的衔接关系确定到达换乘站点的时间协调,而不单纯追求同时到达同一换乘站点的车辆数或车次数最大,提高了站点的换乘效率。公交到站时间协调分布见图 1。
|
| 图 1 各级公交到站时间协调分布 Fig. 1 Coordinate distribution of arrival time of different transit levels |
| |
图 1中,T为公交运营周期;a,b,c为不同时刻。本文旨在优化发车时刻使各层级车辆,到站时间分布集中在a~c范围内。
2 构建多目标优化模型 2.1 问题假设(1) 换乘站点处,乘客只等1条线路的公交车;(2)票价统一,无换乘优惠;(3)站间行程时间固定。
2.2 发车间隔-企业运营效益模型发车间隔直接影响到公交对乘客的吸引情况和公交企业车辆数的投入、运行油耗、驾驶员工资和车辆折旧费用。本文构建的发车间隔-企业运营效益模型如式(1)所示。
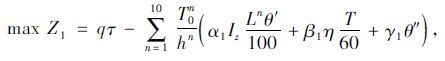
|
(1) |
式中,Z1为企业运营效益;q为调度周期内公交乘客需求量;τ为公交票价;n为公交线路编号,本文中n={1,2,…,10};T0n为各条线路运营周期;hn为各条线路发车间隔;α1,β1,γ1分别为公交油耗、驾驶员工资、车辆折旧在公交企业运营成本中所占比例;Iz为油耗转换为企业运营费用的系数;Ln为优化周期内各条公交线路运营里程;θ′为单车百公里油耗;η为驾驶员工资;T为优化时段,设为1 h;θ″为车辆折旧。
2.3 发车时刻-乘客出行时间成本模型出行时间主要由候车时间、换乘等车时间和在车时间构成。从出发地到站点的时间与到站下车至目的地的时间在线网站点优化过程中已考虑。乘客需要换乘的公交线路如果不同时到达换乘站点,将会产生乘客在站点的等车时间,损失乘客利益。乘客出行时间费用Z2表示为:
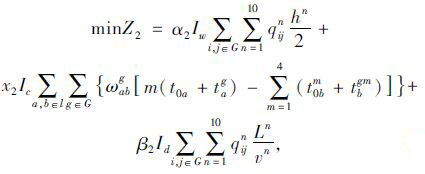
|
(2) |
s.t.最早和最晚发车时刻:
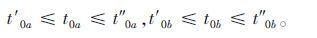
|
(3) |
满载率:
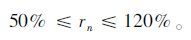
|
(4) |
最大最小发车间隔:
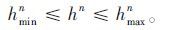
|
(5) |
到站时间协调控制:
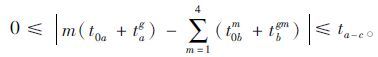
|
(6) |
式(2)~式(6)中,α2,x2,β2分别为候车时间、换乘时间和在车时间占公交乘客出行时间的比例;Iw,Ic,Id分别为候车时间、换乘时间和在车时间转换为乘客出行费用的系数;G为公交站点集合;i,j分别为公交线网中第i,j个站点;g为换乘站点,公交站点i,j,g∈G;l为线路集合,l={ln},a,b∈l;qijn为公交站点i-j之间第n条公交线路上的乘客数;hn为各条线路发车间隔;ωabg为换乘站点g处线路a与b间的换乘人数;m为在同一个换乘站点处与较高服务层级线路有换乘关系的较低层级线路条数;t0a,t0b分别为优化周期内线路a,b的始发车时间;tag,tbg分别为线路a,b的车辆从始发站到换乘站点g的行程时间;Ln为调度周期内各条公交线路运营里程;vn为第n条公交线路的行驶速度;t
公交时刻表模型涉及多个参数和变量,综合对比各种算法特点,本文选择遗传算法、粒子群优化算法和遗传粒子群优化算法分别求解该模型。算法在求解多目标优化问题上的适用性依次表现为:
遗传算法:(1)具有搜索的多向性和全局性,能够在一次运行中获取多Pareto最优解;(2)可以处理所有类型的目标函数和约束;(3)采用基于种群的方式组织搜索、遗传操作和优胜劣汰的选择机制,不受搜索空间条件限制。
粒子群优化算法:(1)直接根据被优化问题进行实数编码;(2)对种群的初始化不敏感,可达到较快的收敛速度;(3)优化过程中,每个粒子通过自身经验与群体经验进行更新,具有学习和记忆功能;(4)在收敛性、解的分布及计算效率方面都有很大改善。
遗传粒子群优化算法:(1)对两种算法取长补短,将粒子群算法中实数编码的相关操作引入遗传算法;(2)在粒子群算法中增加遗传算法的选择、交叉操作,改进种群分割策略。
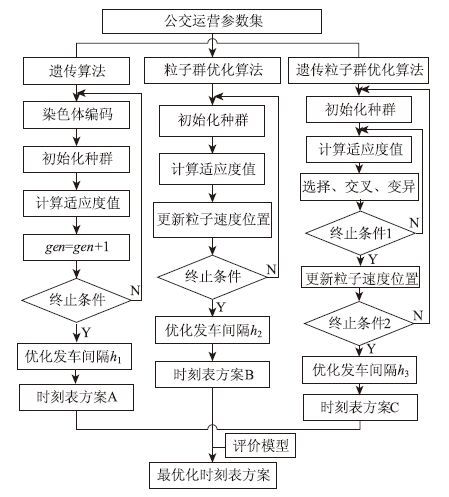
3.2 计算步骤公交区域时刻表优化模型的计算流程如图 2所示。
|
| 图 2 常规公交区域时刻表优化模型求解流程图 Fig. 2 Flowchart of conventional bus regional timetable optimization model solving |
| |
4 优化结果与分析
将8:00-9:00时段采集到的客流量作为模型基本客流输入,最大最小发车间隔的计算参看文献[9],模型中涉及到的参数值依次为:n=10;l1={2路,3路},l2={5路,7路,8路},l3={1路,4路,10路},l4={6路,9路};Iw=10元/h;Ic=14元/h;Id=8元/h;Iz=8元/h;θ′=25 L/(100 km);η=10元/h;θ″=8元/(辆·h);α1=0.4;β1=0.3;γ1=0.3;α2=0.3;x2=0.4;β2=0.3;rn=0.75。
遗传算法主要参数设置:变量类型为实数,种群规模为40,交叉概率为0.8,选择方法为轮盘赌,交叉方法为均匀交叉,变异方法为正态分布,收敛标准为1e-6;
粒子群优化算法主要参数设置:粒子群规模为40,最大迭代次数为100,学习因子C1和C2均为2;惯性权重w为0.73。
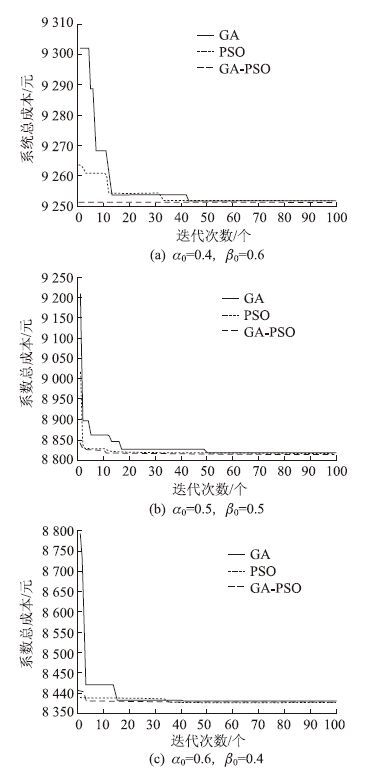
将发车间隔分别作为遗传算法(GA)中的染色体、粒子算法(PSO)的粒子和遗传粒子群优化算法(GA-PSO)的染色体(粒子)。运用MATLAB R2010b软件求解模型,令α0和β0分别为目标函数权重,当取不同目标权重值时,算法优化过程及结果如图 3所示。
|
| 图 3 不同权重值时,3种算法优化过程及结果 Fig. 3 Optimization process and results by 3 algorithms with different weights |
| |
分析图 3,发现3种情况下遗传粒子群优化算法的精度和收敛效率均优于遗传算法和粒子群优化算法。可见,在该公交时刻表优化模型中遗传粒子群算法更优越。因此下文均采用遗传粒子群优化算法的计算结果作为模型的最优解。
依据运行结果,得到8:00-9:00时段内整个公交线网10条线路的发车间隔。对车辆数向上取整,得到不同权重目标值情况下基于线网布局的公交区域时刻表优化方案,见表 2。
| 线路编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 合计 |
| α0=0.4 发车间隔/min | 15 | 5 | 5 | 15 | 10 | 25 | 10 | 10 | 20 | 15 | 79 |
| β0=0.6 车辆数/辆 | 6 | 19 | 17 | 5 | 7 | 2 | 7 | 9 | 2 | 5 | |
| α0=0.5 发车间隔/min | 18 | 6 | 6 | 18 | 12 | 25 | 12 | 12 | 20 | 18 | 72 |
| β0=0.5 车辆数/辆 | 5 | 17 | 16 | 4 | 6 | 2 | 7 | 8 | 2 | 5 | |
| α0=0.6 发车间隔/min | 19.5 | 6.5 | 6.5 | 19.5 | 13 | 25 | 13 | 13 | 20 | 19.5 | 69 |
| β0=0.4 车辆数/辆 | 5 | 16 | 16 | 4 | 5 | 2 | 7 | 7 | 2 | 5 |
通过进一步论证基于公交线网布局的区域协调时刻表方案的优越性,为方案选择提供依据。从公交企业运营效益和乘客出行时间成本两个方面,分别与优化前时刻表方案取3种权重值计算得到的目标函数值进行比较,如表 3所示。
| 权重值 | 遗传粒子群优化方案 | |||||
| 企业运 营收益/ 元 | 变化 比例/ % | 乘客出 行时间 成本/元 | 变化 比例/ % | 系统总 成本/ 元 | 变化 比例/ % | |
| α0=0.4,β0=0.6 | 5 992.38 | +0.78 | 11 423.58 | -8.63 | 9 251.1 | -3.48 |
| α0=0.5,β0=0.5 | 6 028.65 | +1.37 | 11 699.15 | -6.08 | 8 863.9 | -5.47 |
| α0=0.6,β0=0.4 | 6 119.62 | +2.92 | 11 762.32 | -5.22 | 8 376.7 | -8.42 |
分析表 3,当取不同目标权重值时,优化效果略有差异。但总体上优化后给企业带来了较好的经济效益。优化后的乘客出行时间成本相对于优化前均明显减少,公交服务质量得到了很好的提高,使公交运营能发挥更好的社会效益。
5 结论本文基于对公交线网衔接模式的研究,从公交运营企业与乘客双赢的角度出发,构建了多目标优化模型。分析了线路组合运营和换乘协调对乘客出行时间的影响。选用遗传算法、粒子群优化算法和遗传粒子群优化算法求解模型。实例计算结果验证了遗传粒子优化算法对基于线网衔接的区域公交时刻表优化模型的优化效果更为明显。实际线网由10条线路组成,扩充了研究的运用范围,为理论成果在实践中的应用奠定了基础。
在实际中,需要根据给定的运营效益和乘客出行时间成本权重值选定时刻表优化方案。本文假设公交车辆站间行驶时间为常数,与实际车辆运行规律有一定的差异,因此,在下一步研究中需要引入行程时间的变化特征。
| [1] | SALZBORN F J M. Scheduling Bus Systems with Interchanges[J]. Transportation Science , 1980, 14 (3) : 211-231 |
| [2] | SHRIVASTAVA P, O'MAHONY P. A Model for Development of Optimized Feeder Routes and Coordinated Schedules:A Genetic Algorithms Approach[J]. Transport Policy , 2006, 13 (5) : 413-425 |
| [3] | HALL R W. Vehicle Scheduling at a Transportation Terminal with Random Delay En-route[J]. Transportation Science , 1985, 19 (3) : 308-320 |
| [4] | ABKOWITZ M, JOSEF R, TOZZI J, et al. Operational Feasibility of Timed Transfer in Transit Systems[J]. Journal of Transportation Engineering , 1987, 113 (2) : 168-177 |
| [5] | MAXWELL R R. Intercity Rail Fixed-interval, Timed-transfer, Multi-hub System:Applicability of the "Integraler Taktfahr Plan" Strategy to North America[J]. Transportation Research Record , 1999, 1691 : 1-11 |
| [6] | ZHAO F, ZENG X G. Optimization of Transit Route Network, Vehicle Headways and Timetables for Large-scale Transit Networks[J]. European Journal of Operational Research , 2008, 186 (2) : 841-855 |
| [7] | 司徒炳强.公交网络时刻表编制的理论建模及可靠性控制方法研究[D]. 广州:华南理工大学,2011. SITU Bing-qiang. Research on Theoretical Modelling and Reliability Control Method for Timetable of Bus Network[D]. Guangzhou:South China University of Technology, 2011. http://www.oalib.com/references/16921763 |
| [8] | 陈霞.基于线网结构的公交协同研究[D].长沙:长沙理工大学,2011. CHEN Xia. Public Traffic Collaboration Based on Network Structure[D].Changsha:Changsha University of Science and Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10536-1012274416.htm |
| [9] | 宋同阳.区域公交调度时刻表优化研究[D]. 武汉:华中科技大学,2013. SONG Tong-yang. Research on Regional Bus Timetable Scheduling Optimization[D]. Wuhan:Huazhong University of Science and Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10487-1014029673.htm |
 2016, Vol. 33
2016, Vol. 33
