扩展功能
文章信息
- 荀敬川, 贺拴海, 高俊亮
- XUN Jing-chuan, HE Shuan-hai, GAO Jun-liang
- 基于数据驱动的随机子空间优化算法及应用
- An Algorithm for Stochastic Subspace Optimization Based on Data-driven and Application
- 公路交通科技, 2016, 33(12): 93-100
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(12): 93-100
- 10.3969/j.issn.1002-0268.2016.12.015
-
文章历史
- 收稿日期: 2016-05-16
2. 北京新智交科科技开发有限公司, 北京 100010
2. Beijing New Intelligent Transport Science and Technology Development Co., Ltd., Beijing 101100, China
模态分析技术可分为3大类[1]:其一是基于计算机仿真的有限元分析法(Finite Element Analysis,FEA);其二为基于输入(激励)/输出(响应)模态试验模态分析法(Experimental Modal Analysis,EMA);其三是基于仅有输出(响应)模态试验的运行模态分析法(Operational Modal Analysis,OMA)。第一类属于结构动力学正问题,第二类与第三类属于结构动力学反问题。基于仅有输出(响应)的模态参数识别技术(OMA),因其无需增加特殊的激励设备,基本不影响结构的正常运行,对结构损伤小,测试费用低等优点,被广泛应用于土木工程领域[2]。
模态参数(固有频率、阻尼比、振型)识别是结构动力学特性分析、结构健康监测、损伤识别等方面的关键内容,特别是对于服役期桥梁健康监测,能否利用在线监测数据实时识别模态参数,对识别方法及算法提出来更高的挑战。随机子空间识别法(Stochastic Subspace Identification,SSI)以其输入参数少,可程序化程度高等优点受到国内外学者的热捧。SSI假定输入信号为随机白噪声,利用自然环境激励条件下进行结构模态参数识别,基于离散时间状态空间方程,直接处理时间序列的时域方法。比利时鲁汶大学的Bart Peeter等人提出基于数据的子空间识别的概念及思想,并把系统控制理论与矩阵理论联系起来,利用稳定图确定系统的阶次[3-4];福州大学任伟新教授团队提出基于稳定图的平均正则化稳定图算法,使得模态参数识别效率和识别精度得到提高,提炼出经验模式分解(EMD)的SSI,并应用于桥梁和建筑物等工程实例[5-6];同济大学的孙利民、张启伟、常军等人提出两阶段稳定图方法剔除虚假模态,消除模态遗漏现象,对Hankel矩阵中的“过去”输出数据缩减,以提高计算效率[7-8];重庆大学的章国稳、汤宝平课题组利用谱系聚类法实现模态参数的自动识别,依据模态能量水平剔除虚假模态,提出基于数据缩减的分频段小波变换模态参数快速自动识别[9];刘兴汉、王跃宇等人提出基于Cholesky分解的改进随机子空间识别法,通过对维数大大减少的Cholesky分解来得到投影矩阵,提高计算效率[10];此外,香港理工大学、东南大学、清华大学、西北工业大学等多所科研院校对SSI进行了深入的研究和探讨。
经过40余年的发展,国内外研究学者在SSI方法上取得很大成就,但是仍面临许多问题,特别是SSI方法的计算效率有待提高。基于数据驱动SSI方法,需要构造单无限大的Hankel矩阵,需要处理的数据非常庞大,并且涉及到高维QR分解和SVD分解,需要的时间和内存开销很大程度上影响了其在实际工程中的应用。针对以上问题,本文对基于数据驱动SSI方法进行优化,首先,以部分测点信息作为“过去”输出信号代替全部测点信号,精简Hankel矩阵中的“过去”输出数据Yp,减少计算量,针对文献[7]可能出现模态遗漏的问题,本研究通过基于模态置信度(Modal Assurance Criterion,MAC)的数据优化,有效避免模态遗漏。其次,通过公式推导,避开求解投影矩阵简化计算步骤,避免高维矩阵的分解和存储,改善计算机使用内存,提高计算效率。最后,以西宁北川河桥为工程实例,验证该优化算法的实用性和有效性。
1 结构振动的状态空间模型的计算法结构振动微分方程为:
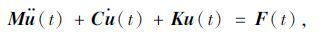
|
(1) |
式中,M∈Rn×n,C∈Rn×n,K∈Rn×n分别为质量矩阵、阻尼矩阵、刚度矩阵;u(t)∈Rn为位移向量;F(t)∈Rn×l外部激励向量。
令
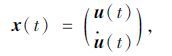
|
(2) |
则式(1)可转化为:
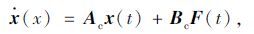
|
(3) |
引入观测方程:
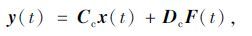
|
(4) |
式中,y(t)∈Rl×1为观测向量(l表示测点数);Ac∈R2n×2n为连续状态矩阵;Bc∈R2n×2n为连续时间输入矩阵;Cc∈Rl×2n为连续时间输出矩阵;Dc∈Rl×m为直馈矩阵。
自然环境激励通常为风、车辆或行人等,假定是理想的白噪声激励,并与输入噪声和输出噪声合并,将式(3)与式(4)离散化可得离散时间状态空间模型:
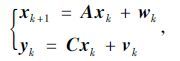
|
(5) |
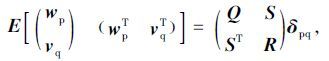
|
(6) |
式中,yk∈Rl×1为第k(k∈N)个采样间隔(Δt)的输出向量;xk∈R2n×1为状态向量;A∈R2n×2n为离散状态矩阵;C∈Rl×2n为离散输出矩阵;E为数学期望算子,δpq为Kronecker Delta函数;wk∈Rl×1,vk∈R2n×1为测量噪声、过程噪声;Q∈R2n×2n,S∈R2n×l和R∈Rl×l为噪声序列wk,vk的协方差矩阵。
2 随机子空间优化算法SSI可分为:基于协方差驱动随机子空间识别法(Cov-SSI)与基于数据驱动随机子空间识别法(Data-SSI),其基本原理都是以线性系统的最小实现理论为基础,利用Hankel 矩阵与系统可观测性、可控制性矩阵的特殊关系求得系统矩阵A和输出矩阵C,在状态空间辨识系统的模态参数。SSI利用矩阵分析QR分解使得数据缩减,采用奇异值分解(SVD)剔除噪声干扰,运用最小二乘法来识别系统的状态矩阵,最后通过特征值分解直接确定结构模态参数:自振频率、阻尼比和振型。
2.1 构造Hankel矩阵构造Hankel矩阵时,数据量很大(单无限),虽然现在计算机硬件得到很好的改善,但Hankel矩阵的QR分解会消耗计算机很大内存,计算耗时长。
2.1.1 基于MAC准则的数据优化根据结构响应的特点,各个测点的输出信号都包含相同的频率信号-固有频率,由投影原理可知,所有的输出信号都可以单独或者部分组合作为被投影信号,即精简“过去”输出数据Yp,但是牺牲参与信息以减少计算量伴随有模态遗漏等问题。为避免各向量之间的交角偏小让系统遗漏关键模态的情况发生,MAC算法可以在选择测点数据时,使量测的模态向量保持较大的空间交角,增大模态向量的识别效果,尽可能地保留原模型的特性,模态置信度MAC矩阵(简称M阵)表达式如下:
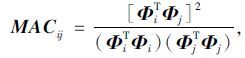
|
(7) |
式中,Φi和Φj分别为第i阶和第j阶模态向量。通过检查各模态在量测自由度上形成的向量M阵的非对角元,即可判断出相应两模态向量的交角情况。当M阵的某一元素Mij (i≠j)等于1时表明第i向量与第j向量交角为零,两向量不可分辨;而当Mij(i≠j)等于零时,则表明第i向量与第j向量相互正交,两向量可以轻易识别。故选择数据的测点布置应力求使M阵非对角元向最小化发展,一般建议非对角元最大取值为0.25[11]。
当从全部测点数据中删除k行,式(17)变为:
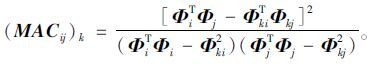
|
(8) |
从已有测点数据里删除某点数据是一个反复迭代,不断寻优的过程,其根本目的是删除使M阵非对角元最大的测点数据。
2.1.2 构造数据精简的Hankel矩阵从l个测量数据中选择r个作为“过去”输出数据,即:
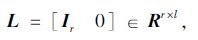
|
(9) |
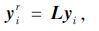
|
(10) |
式中,L为选择矩阵;Ir为r阶单位对角矩阵;yir为i时刻“过去”输出信号的块元素;yi为使得M阵非对角元减小最快测点至最慢测点重新排列后的i时刻所有输出信号的块元素。
构造Hankel矩阵:
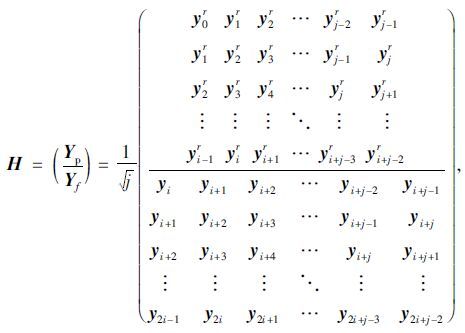
|
(11) |
式中,“过去”输出数据Yp∈Rri×j;“将来”输出数据Yf∈Rli×j。
2.2 Hankel矩阵QR分解SSI通过QR分解对Hankel矩阵进行数据缩减:
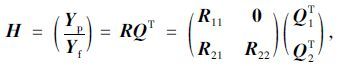
|
(12) |
式中,Q为正交矩阵:QTQ=QQT=I;R为下三角矩阵。
Yf向Yp的投影矩阵[7]:
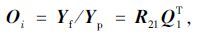
|
(13) |
定义可观测矩阵:

|
(14) |
则投影矩阵可表示为:
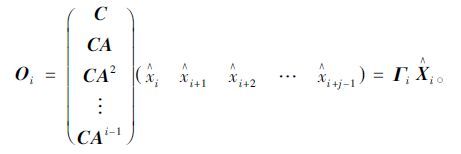
|
(15) |
Data-SSI传统的计算方法,投影矩阵Oi贯穿整个计算过程,但是投影矩阵的列数与Hankel矩阵列数相同,依然是单无限,并且求解过程很复杂,如果能避开求解投影矩阵,不仅减少计算步骤,还能改善计算机内存,从而提高计算效率。
可观测矩阵Γi与投影矩阵Oi相关联,投影矩阵Oi又可用矩阵R21表示,如果能找到可观测矩阵Γi与矩阵R21的关系式,就可以避免求解投影矩阵,推导如下:
对矩阵R21进行奇异值(SVD)分解:
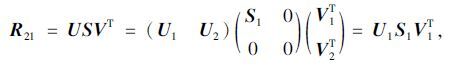
|
(16) |
式中,U,V属于酉矩阵;S=diag(σ1,σ2,…,σn),σi为从大到小的全部非零奇异值。
则式(13)可表示为:
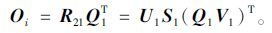
|
(17) |
根据矩阵运算的性质[12],Q1T属于正交矩阵,必属于酉矩阵;两个酉矩阵的乘积Q1V1必属于酉矩阵,由此推知式(17)为投影矩阵Oi奇异值分解的一种形式。
则可观测矩阵可表示为[7]:
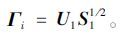
|
(18) |
至此,可观测矩阵Γi与矩阵R21的SVD分解建立关系,优化算法避免了求解投影矩阵Oi,Hankel矩阵QR分解时只存储下三角矩阵R,利用子矩阵R21的SVD分解求得可观测矩阵Γi。计算过程中避开了大矩阵的存储和分解(R21要比Oi小很多),并且不用存储正交矩阵Q,改善了计算机的使用内存,提高了计算效率。
2.4 求解系统矩阵A和C定义观测矩阵Γi的两个子阵Γ1和Γ2:
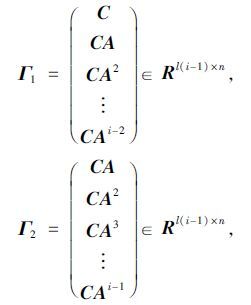
|
(19) |
系统矩阵A:
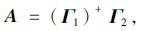
|
(20) |
式中,(•)+表示矩阵的伪逆。
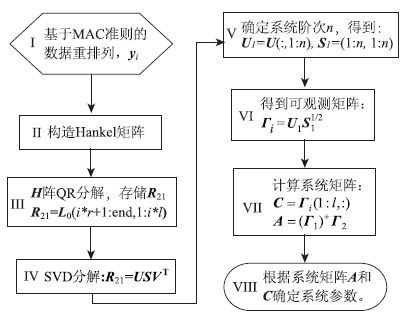
通过观测矩阵Γi求得系统矩阵A与C,实际工程应用中,在确定系统阶次时结合稳定图的方法计算不同的A,C从而识别系统参数。
|
| 图 1 SSI优化算法流程图 Fig. 1 Flowchart of optimization algorithm by SSI |
| |
3 工程算例
本文采用与文献[7, 13-14]相同的工程实例,中承式钢管混凝土系杆拱桥-西宁北川河桥为工程实例,便于比较计算方法的有效性。
3.1 工程概况西宁北川河桥,净跨90 m,矢跨比1/5,拱轴线为悬链线,拱轴系数m=1.167;桥面净宽21.6m,共16对吊杆;主拱圈采用4根φ650 mm×10 mm 钢管,内灌注C50混凝土,横梁采用C40钢筋混凝土,吊杆采用127×φ5高强碳素钢丝,水平系杆选用φ5高强钢丝束。
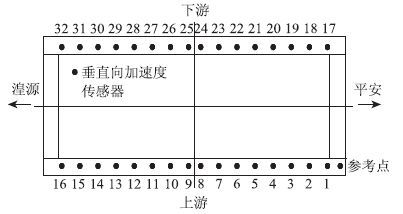
环境激励是利用自然风载、随机交通荷载或其他环境激励及其组合等,测量桥梁的动力特性,具有简单易行、不中断交通、对桥梁结构的损伤小、测试费用低等优点,应用越来越广泛。全桥上下游每侧布置竖向测点16个,共32个,位于每根吊杆下侧,一个固定参考点,位于桥面起始处,传感器横向布置如图 2所示。全桥共分4组进行测试,每组8个测点,信号采样频率80 Hz。以20 Hz重采样、组成36行18176列的原始数据。
|
| 图 2 加速度传感器布置图 Fig. 2 Arrangement of acceleration transducers |
| |
3.2 数据优选
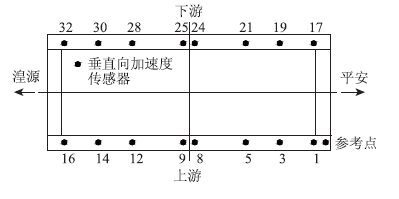
首先确定竖向弯曲振动特征作为有效振型,提取对桥梁的竖向振动有贡献的前4阶振型数据来考虑作为数据优选的原始数据,并将这4阶振型组成模态向量矩阵(模态向量选用文献[14]方法识别结果)。然后以全部测点为初始状态进行筛选,利用MAC法,依次删除使得MAC阵非对角元减少最小的测点数据,剩余测点数据为候选,反复迭代,逐步删除更多测点数据,直到满足预设值要求(即MAC阵非对角元小于0.05),并依次记录删除测点信息。最后,按照测点删除顺序反向排列测点数据,即最先删除测点排列到最后,保留测点排列前几行。最终优化测点布置方案如图 3所示。
|
| 图 3 优选测点方案 Fig. 3 Scheme of measuring point optimization |
| |
3.3 检验与对比分析
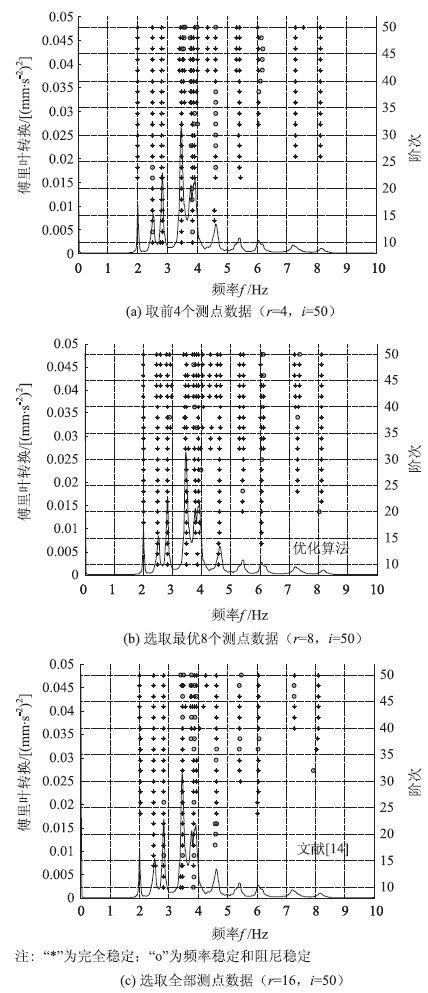
基于Matlab平台,使用C语言编写程序,识别桥梁结构的频率,以相同的标准:最小阶次取10,最大阶次取50;稳定点个数取15;判定标准:频率0.01、阻尼0.4、振型0.05。图 4中连续曲线为平均正则化功率谱,峰值法提取的频率与SSI识别频率形成直观对比。
|
| 图 4 不同算法的稳定图对比 Fig. 4 Comparison of stability diagrams obtained by different algorithms |
| |
当r=4,i=50,无数据优选,即取前4个测点数据作为“过去”输出数据:Yp∈R200×18 176,Yf∈R800×18 176,形成的稳定图见图 4(a)。
当r=8,i=50时:Yp∈R400×18 176,Yf∈R800×18 176,本文优化算法形成的稳定图见图 4(b)。
文献[14]选用桥梁一侧全部的16个测点数据,无数据优选,i=50时:Yp∈R800×18 176,Yf∈R800×18 176,形成的稳定图见图 4(c)。
观察图 4(a)第4阶频率(4.589)完全稳定次数只有9次,无法提取,形成遗漏。对比图 4(a)与(b),前4阶频率完全稳定次数都有所增加,特别是第4阶频率全部完全稳定,将成为优势频率。观察图 4(c)可知,文献[14]算法的第4阶频率(4.589)完全稳定次数12次,第一阶频率(2.014)完全稳定次数14次,如果要提取前4阶频率,稳定点个数标准应降低到12次。观察图 4(b),本文优化算法前4阶频率完全稳定次数依次是:17,22,22,22,3个稳定图中都是最多。通过以上分析,r取值受到振型稳定的影响,不宜太低并且与选择的位置相关,本文优化算法通过数据优选有效地解决了此问题,避免了模态遗漏;在识别高阶次模态时,为避免形成更多的虚假模态,完全稳定次数的提高为判定标准提供更广的选择空间。
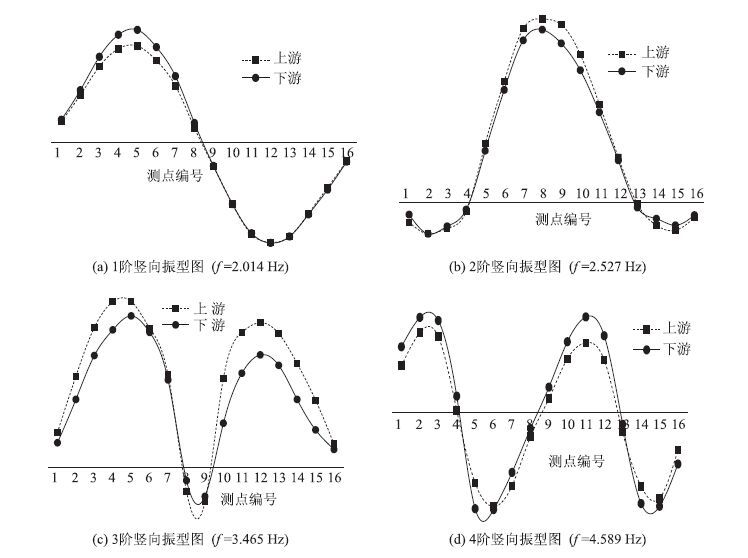
各文献及本文优化算法识别的频率如表 1所示,对比各组数据,本文优化算法结构与其他方法差别不大,误差范围在5%以内。优化算法识别结果比较理想。优化算法的前4阶竖向振型如图 5所示。
| 模态 | 有限元法/Hz | 峰值法/ Hz | 文献[7] | 文献[14] | 本文算法 | |||
| 实测/Hz | 误差/% | 实测/Hz | 误差/% | 实测/Hz | 误差/% | |||
| 1阶竖向 | 1.966 | 2.012 | 2.02 | -2.7 | 2.004 | -1.9 | 2.014 | -2.4 |
| 2 阶竖向 | 2.638 | 2.519 | 2.58 | 2.2 | 2.511 | 5.1 | 2.527 | 4.4 |
| 3 阶竖向 | 3.501 | 3.457 | 3.47 | 0.9 | 3.466 | 1.0 | 3.465 | 1.0 |
| 4 阶竖向 | 4.512 | 4.628 | 4.67 | -3.4 | 4.598 | -1.9 | 4.589 | -1.7 |
| 注:1.误差=(有限元值-实测值)/ 实测值;2.有限元法和峰值法数据来自文献[13]。 | ||||||||
|
| 图 5 前4阶竖向振型图 Fig. 5 First 4 orders vertical model shapes |
| |
耗时方面,以下所有耗时均采用同一计算机:windous XP系统、3G内存。
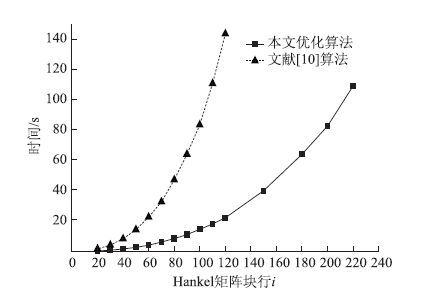
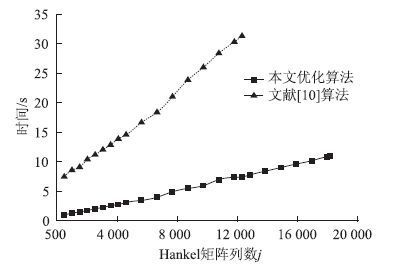
如果Hankel矩阵j取5 000列,i取50块行,文献[14]算法需要14.641s,本文优化算法仅需3.045 s,识别时间仅为前者的20.8%。如果Hankel矩阵的列取5 000固定不变,二者耗时对比如图 6所示,随着块行数的增加,本文优化算法优势越来越明显,当块行数i大于120时,文献[14]的算法由于内存超界(out of memory)而无法计算。如果Hankel矩阵i取50不变,文献[14]算法的识别时间约是本文算法的5倍,如图 7所示,并且当列数j大于12 500时,前者算法因内存超界而无法计算。观察图 6、图 7,块行i增加对识别时间的影响远远大于列j,识别时间随i呈指数增长,随j呈线性趋势增长;Hankel矩阵的行数为2li或者(r+l)i行,Hankel矩阵的大小对i的变化更敏感所致。
|
| 图 6 j=5 000不变,时间随i的变化 Fig. 6 j=5 000,time varying with i |
| |
|
| 图 7 i=50不变,时间随j的变化 Fig. 7 i=50,time varying with j |
| |
4 结论
本文推导了SSI优化算法,并通过工程算例分析及对比验证了其实用性和有效性。在稳定图中包含了平均正则化功率谱,相互校核,确保识别结果的可靠性,本文优化算法具有如下优点:
(1) 通过MAC准则优化选取数据,缩减了Hankel矩阵的“过去”输出数据Yp,有效避免了由于数据减少带来模态遗漏;
(2) 避开求解投影矩阵Oi,利用Hankel矩阵R21求得可观测矩阵Γi;
(3) 计算过程中避开了高维矩阵的存储、QR分解和SVD分解,减少了计算量,并且不用存储正交矩阵Q,很大程度上改善了计算机的使用内存。
通过图 6和图 7可以明显看出,本文优化算法耗时更短,在相同计算机配置下,该算法处理的数据能力更强大,特别是对于梁拱组合桥、斜拉桥、悬索桥等需要处理海量数据的柔性结构,该算法更具优势。同时,由于识别速度快、方法稳定、精度高等优点,成为桥梁的健康监测、桥梁在线损伤识别和评估等领域更有力的工具。
| [1] | 陈伏彬, 李秋胜. 基于环境激励的大跨结构动力特性识别[J]. 地震工程与工程振动 , 2015, 35 (1) : 58-65 CHEN Fu-bin, LI Qiu-sheng. Identification of Dynamic Characteristics of Large-span Structure Based on the Ambient Excitation[J]. Earthquake Engineering and Engineering Vibration , 2015, 35 (1) : 58-65 |
| [2] | IVANOVIC S S, TRIFUNAC M D, TODOROVSKA M I. Ambient Vibration Tests of Structures-a Review[J]. ISET Journal of Earthquake Technology , 2000, 37 (4) : 165-197 |
| [3] | PEETER B, MAECK J, DE ROECK G. Reference-based Stochastic Subspace Identification for Output-only Modal Analysis[J]. Mechanical Systems and Signal Processing , 1999, 13 (6) : 855-878 |
| [4] | PEETER B, MAECK J, DE ROECK G. Excitation Sources and Dynamic System Identification in Civil Engineering[C]//Proceedings of European COST F3 Conference on System Identification and Structural Health Monitoring. Leuven:Catholic University of Louvain, 2000:341-350. |
| [5] | 任伟新. 环境振动系统识别方法的比较分析[J]. 福州大学学报:自然科学版 , 2001, 29 (6) : 80-86 REN Wei-xin. Comparison of System Identification Methods Using Ambient Vibration Measurements[J]. Journal of Fuzhou University:Natural Science Edition , 2001, 29 (6) : 80-86 |
| [6] | 禹丹江, 任伟新. 基于经验模式分解的随机子空间识别方法[J]. 地震工程与工程振动 , 2005, 25 (5) : 63-68 YU Dan-jiang, REN Wei-xin. Empirical Mode Decomposition Based Stochastic Subspace Identification[J]. Earthquake Engineering and Engineering Vibration , 2005, 25 (5) : 63-68 |
| [7] | 常军.随机子空间方法在桥梁模态参数识别中的应用研究[D].上海:同济大学,2004. CHANG Jun. Bridge Modal Parameters Identification by Stochastic Subspace Method[D]. Shanghai:Tongji University, 2004. |
| [8] | 常军, 孙利民, 张启伟. 随机子空间识别方法计算效率的改进[J]. 地震工程与工程振动 , 2007, 27 (3) : 88-94 CHANG Jun, SUN Li-min, ZHANG Qi-wei. Improvement in Stochastic Subspace Identification[J]. Earthquake Engineering and Engineering Vibration , 2007, 27 (3) : 88-94 |
| [9] | 章国稳. 环境激励下结构模态参数自动识别与算法优化[D].重庆:重庆大学,2012. ZHANG Guo-wen. Modal Parameter Automatic Identification and Algorithm Optimization for Structures under Ambient Excitation[D]. Chongqing:Chongqing University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10611-1012047292.htm |
| [10] | 刘兴汉, 王跃宇. 基于Cholesky分解的改进的随机子空间法研究[J]. 宇航学报 , 2007, 28 (3) : 608-612 LIU Xing-han, WANG Yue-yu. Improved Stochastic Subspace Identification Based on Cholesky Factorization[J]. Journal of Astronautics , 2007, 28 (3) : 608-612 |
| [11] | 宗周红, 孙建林, 徐立群, 等. 大跨度连续刚构桥健康监测减速度传感器优化布置研究[J]. 地震工程与工程振动 , 2009, 29 (2) : 150-158 ZONG Zhou-hong, SUN Jian-lin, XU Li-qun, et al. Study on Optimal Placement of Acceleration Sensors for Health Monitoring of a Long-span Continuous Rigid-frame Bridge[J]. Earthquake Engineering and Engineering Vibration , 2009, 29 (2) : 150-158 |
| [12] | 张凯院, 徐仲, 吕全义, 等. 矩阵论[M]. 北京: 科学出版社, 2013 . ZHANG Kai-yuan, XU Zhong, LÜ Quan-yi, et al. Matrix Theory[M]. Beijing: Science Press, 2013 . |
| [13] | 宗周红, BijayaJaishi, 林友勤, 等. 西宁北川河钢管混凝土拱桥的理论和实验模态分析[J]. 铁道学报 , 2003, 25 (4) : 89-96 ZONG Zhou-hong, Bijaya Jaishi, LIN You-qin, et al. Experimental and Analytical Modal Analysis of a CFT Arch Bridge over Xining Beichuan River[J]. Journal of The China Railway Society , 2003, 25 (4) : 89-96 |
| [14] | 高俊亮, 王国清, 彭彦忠, 等. 改进的数据驱动的随机子空间算法在桥梁监测中的应用[J]. 河北工业大学学报 , 2012, 41 (6) : 83-87 GAO Jun-liang, WANG Guo-qing, PENG Yan-zhong, et al. Application of Improved Data-driven Stochastic Subspace Algorithms in Bridge Monitoring[J]. Journal of Hebei University of Technology , 2012, 41 (6) : 83-87 |
| [15] | 章国稳, 汤包平, 孟利波. 基于特征值分解的随机子空间算法的研究[J]. 振动与冲击 , 2012, 31 (7) : 74-78 ZHANG Guo-wen, TANG Bao-ping, MENG Li-bo. Improved Stochastic Subspace Identification Algorithm Based on Eigendecomposition[J]. Journal of Vibration and Shock , 2012, 31 (7) : 74-78 |
| [16] | 王济, 胡晓. MATLAB在振动信号处理中的应用[M]. 北京: 中国水利水电出版社, 2006 . WANG Ji, HU Xiao. Application of MATLAB in Vibration Signal Processing[M]. Beijing: China Waterpower Press, 2006 . |
 2016, Vol. 33
2016, Vol. 33
