扩展功能
文章信息
- 赵全满, 张洪亮, 周浩
- ZHAO Quan-man, ZHANG Hong-liang, ZHOU Hao
- 基于离散元的水泥混凝土细观模拟试验
- Simulation Test of Cement Concrete in Meso-scale Based on Discrete Element Method
- 公路交通科技, 2016, 33(12): 48-55
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(12): 48-55
- 10.3969/j.issn.1002-0268.2016.12.008
-
文章历史
- 收稿日期: 2015-08-11
2. 长安大学 公路学院, 陕西 西安 710064
2. School of Highway, Chang'an University, Xi'an Shaanxi 710064, China
水泥混凝土是由集料、胶凝材料及其界面组成的非均匀复合材料,外部荷载作用下其力学性能和破坏过程较为复杂。目前,对于混凝土的数值模拟多采用有限元方法,将混凝土视为连续的均匀材料(尤其是混凝土路面模拟时),虽然在有些条件下满足计算精度的要求,但这与实际情况存在较大差距。离散元方法可将材料离散化,并将材料视为非连续介质,从细观上对混凝土的应力、应变及破坏过程进行模拟,真实地模拟材料的受力状态及破坏过程。
在离散元中,任何材料都是由一个个颗粒组成,其宏观力学特性是通过颗粒之间的相互作用来体现。材料的变形及强度是由空隙及颗粒与颗粒之间的相互作用决定的。进行离散元数值模拟时,可通过改变颗粒之间的细观参数来改变材料的宏观力学特性。国内外已有学者采用离散元方法从细观尺度对材料性能进行研究。You等[1]对沥青混合料的动态模量进行了研究;Abbas等[2]对不同温度下沥青混合料的黏弹性问题进行了研究。刘玉等对集料组成对沥青混合料性能的影响[3]、沥青混合料的黏弹性特性[4]及沥青混合料的蠕变特性[5]等方面进行了研究。王江洋等[6]对沥青混合料单边切口小梁试验进行了模拟,并对荷载作用下沥青混凝土内部裂纹的发展过程进行了研究;冯师蓉等[7]对黏弹性材料的蠕变过程进行了离散元模拟;张东等[8]对级配碎石的动三轴试验进行了模拟;车法等[9]对荷载作用下沥青路面的开裂及扩展进行了模拟;郭红兵[10]和常明丰[11]等对沥青混合料的劈裂试验进行了数值模拟;曲立杰等[12]利用离散元方法建立了沥青路面结构模型,并分析了级配碎石的应力消散功能。可见,采用离散元方法进行数值模拟试验是十分可行的。而且离散元数值模拟试验与室内试验相比,可节省大量的人力、物力和财力,可有效避免由于试验条件、人员操作及环境因素等造成的试验误差,而且离散元方法可从细观尺度对材料在外部荷载作用下的内部受力状态进行分析。
弯拉强度、抗压强度和抗剪强度是水泥混凝土的重要力学指标,利用离散元进行相应的数值模拟试验,从细观尺度对混凝土的力学性能进行研究具有十分重要的意义。因而,论文利用离散元软件PFC2D对水泥混凝土的抗压强度、弯拉强度及抗剪强度试验进行数值模拟,从细观尺度上对混凝土的强度形成机理及破坏过程进行研究。
1 混凝土配合比及强度进行离散元数值模拟之前应获得混凝土的结构组成,才能生成与实际相符的混凝土试件。通过《普通混凝土配合比设计规程》中配合比设计方法计算可知:每立方米混凝土中水泥、水、砂、粗集料的用量分别为398,195,596和1 211 kg。按照10~20 mm档料:5~10 mm档料=7∶3的比例,两档料质量分别为848 kg和363 kg。按照上述级配组成分别成型15×15×15 cm,10×10×40 cm和10×10×30 cm 这3组试件,每组3个,将试件放在养生室养生28 d后,分别进行抗压强度、弯拉强度和抗剪强度试验,试验结果分别为38.7,4.76和4.69 MPa,所得结果将与数值模拟结果进行对比,以验证数值模拟的可行性。
2 抗压强度细观模拟试验在运用PFC2D软件进行混凝土抗压强度模拟时,混凝土的抗压强度是由组成颗粒之间的相互作用决定的。颗粒与颗粒之间的相互作用服从牛顿第二定律,无需满足变形协调及位移连续方程,而且颗粒的位移大小不受限制,因而运用PFC2D软件进行混凝土抗压强度数值模拟试验对混凝土的破坏过程进行研究是十分可行的。模拟试验主要包括以下几个方面:生成颗粒建立数值模型、给颗粒之间赋予细观参数、建立伺服机制控制加载和进行数值模拟试验。为了研究的方便,将混凝土视为由集料、胶凝材料及其界面组成的复合材料来进行模拟试验。在PFC2D中,骨料和胶凝材料用半径不同的圆形颗粒模拟,胶凝材料的黏结作用平行黏结模型[13]模拟。
2.1 模型的建立 2.1.1 模型参数在离散元中,任何结构及物体都是由一个个圆形颗粒组成的,颗粒之间的相互作用决定了物体的宏观力学特性。对于水泥混凝土而言,其抗压强度、弯拉强度及抗剪强度等宏观力学特性是由颗粒之间的相互作用决定的。但是颗粒之间的细观参数无法通过室内试验等宏观力学试验获得,只能通过离散元虚拟试验反复尝试得到。经过反复调试并参考相关文献[3],模型初始推荐参数见表 1。
| 颗粒细观参数 | 平行黏结模型 | ||
| 参数 | 数值 | 参数 | 数值 |
| 颗粒半径/mm | 0.5.1、2.375~4.75和4.75~9.5 | 切向刚度/(N·m-1) | 6×1012 |
| 摩擦系数 | 0.6 | 法向刚度/(N·m-1) | 6×1012 |
| 密度/(kg·m-3) | 2 400 | 黏结半径 | 0.5 |
| 法向刚度/(N·m-1) | 2×109 | 切向强度/(Pa·m-1) | 6×108 |
| 切向刚度/(N·m-1) | 2×109 | 法向强度/(Pa·m-1) | 6×108 |
| 孔隙率 | 0.1 | — | — |
2.1.2 试件的生成
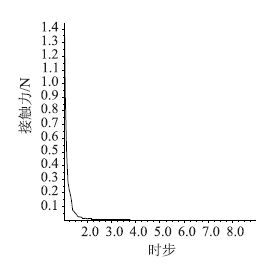
进行抗压强度模拟试验时,试验过程主要包括3个方面:试件的生成、试件的固结及试件加载。试验时,顶面和底面刚性墙体模拟加载板,侧面为自由边界。生成试件宽度和高度均为15 cm,各挡料的比例与第1节相同,5~10 mm和10~20 mm两档粗集料分别用半径为2.375~4.75 mm和4.75~9.5 mm 颗粒模拟,砂和胶凝材料用半径为0.5~1 mm 的颗粒模拟。生成半径为2.375~4.75 mm,4.75~9.5 mm和0.5~1 mm颗粒的数目分别为:68个、50个和5 048个,然后,将细观参数(见表 1)赋予颗粒以模拟胶凝材料的黏结作用,生成试件如图 1所示。最后,采用墙体加载的方式对试件进行加载,运用伺服机制控制加载速度。需要说明的是,试件加载前需保证生成模型已达到平衡,以保证计算结果的精度和可靠性。监测所得平均不平衡力如图 2所示,结果显示试件达到平衡状态(平均不平衡力的大小接近于零)。

|
| 图 1 生成的混凝土试件 Fig. 1 Generated concrete sample |
| |
|
| 图 2 平均不平衡力曲线 Fig. 2 Curve of average unbalanced force |
| |
2.1.3 试验结果及分析
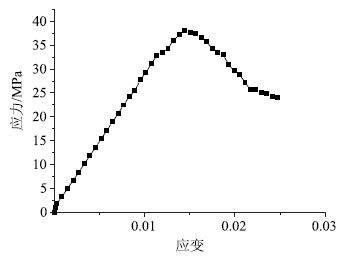
对生成的混凝土试件进行加载,得到不同时步下试件内部颗粒分布状况及力链分布(力链粗细代表了力的大小,越粗表示力越大)见图 3,所得应力-应变曲线图见图 4。由图 3可以看出,加载到6 000 时步时(加载初期),试件内部应力分布较为均匀;加载到20 000时步时,在试件与加载板接触位置开始出现较小的应力集中;加载到30 000时步时,试件内部出现应力集中,开始产生裂缝;加载到45 000 时步时,试件内部产生明显的裂缝,出现明显的滑裂面,试件已经完全破坏。由图 4可知,混凝土试件的抗压强度为38.0 MPa,其弹性模量为29.4 GPa。

|
| 图 3 不同时步时试件颗粒状况及力链分布 Fig. 3 Particle status and force chain distribution of test specimen in different time steps |
| |
|
| 图 4 抗压强度试验应力-应变曲线 Fig. 4 Stress-strain curve for compression strength test |
| |
2.2 影响因素分析
实际中,对混凝土抗压强度和弹性模量的影响因素较多,主要包括水泥用量、水泥强度等级、集料特性、孔隙率等。离散元中,对混凝土抗压强度和弹性模量影响的因素包括摩擦系数、孔隙率、平行黏结半径、平行黏结强度、平行黏结刚度等,本文分别对其进行讨论,找出主要影响因素,为不同强度等级的混凝土提出合理的细观参数推荐值。
(1) 平行黏结半径的影响
宏观上,平行黏结半径代表着混凝土中的水泥掺量,水泥掺量越大,其值越大。平行黏结半径分别取0.3,0.4,0.5和0.6,所得应力-应变曲线见图 5。由图 5可知,随着平行黏结半径的逐渐增加,试件的抗压强度和弹性模量均逐步增加,这与实际情况基本吻合。实际中,随着水泥掺量的逐渐增加,混凝土的强度和弹性模量均逐渐增加。

|
| 图 5 平行黏结半径对抗压强度和弹性模量的影响 Fig. 5 Effects of parallel bond radius on compressive strength and elastic modulus |
| |
(2) 平行黏结强度的影响
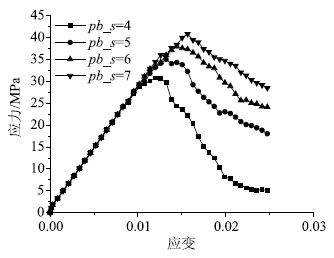
宏观上,平行黏结强度代表着水泥的强度,分别取其为4,5,6和7(单位为1×108 Pa/m),计算所得试件应力-应变曲线见图 6。由图 6可知,随着平行黏结强度的增加,混凝土的抗压强度逐渐增加,平行黏结强度对试件的强度影响较大,但弹性模量基本不变,这与实际情况基本吻合。
|
| 图 6 平行黏结强度对抗压强度和弹性模量的影响 Fig. 6 Effects of parallel bond strength on compressive strength and elastic modulus |
| |
(3) 平行黏结刚度的影响
宏观上,平行黏结刚度代表着集料和胶凝材料界面处的刚度,取其分别为3,5,6和7(单位为1×1012 N/m),计算所得试件应力-应变曲线见图 7。由图可知,平行黏结刚度对试件的抗压强度影响不大,但对试件的弹性模量有一定程度的影响。

|
| 图 7 平行黏结刚度对抗压强度和弹性模量的影响 Fig. 7 Effects of parallel bond stiffness on compressive strength and elastic modulus |
| |
(4) 摩擦系数的影响
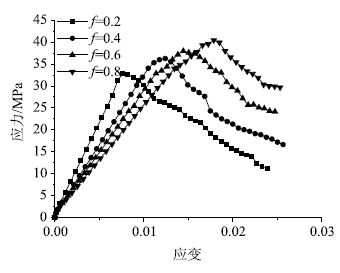
颗粒间的摩擦系数在宏观上代表着集料和砂表面的粗糙程度,取其分别为0.2,0.4,0.6和0.8,计算所得试件应力-应变曲线见图 8。由图 8可知,随着颗粒间摩擦系数的增加,试件抗压强度逐渐增加,弹性模量逐渐减小,颗粒间摩擦系数对混凝土强度及弹性模量影响较大。
|
| 图 8 摩擦系数对抗压强度和弹性模量的影响 Fig. 8 Effects of friction coefficient on compressive strength and elastic modulus |
| |
(5) 孔隙率的影响
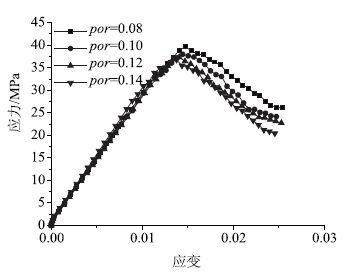
混凝土内部孔隙状况对其强度及模量有一定程度的影响,取其分别为0.08,0.10,0.12和0.14,求得试件应力-应变曲线见图 9。由图 9可知,随着孔隙率的增加,混凝土试件的抗压强度略微增加,弹性模量基本不变。可见,孔隙率对混凝土的强度和模量影响不大。
|
| 图 9 孔隙率对抗压强度和弹性模量的影响 Fig. 9 Effects of porosity on compressive strength and elastic modulus |
| |
通过以上研究发现:在离散元中,模拟试件的抗压强度和弹性模量是多个细观参数综合作用的结果,不同细观参数对其影响程度宜不同;对试件弹性模量影响较大的参数包括摩擦系数、平行黏结刚度和平行黏结半径;对试件抗压强度影响较大的参数包括平行黏结强度、平行黏结半径和摩擦系数。因而,在后文分析中着重分析以上几种因素。
2.3 水泥混凝土细观参数的标定利用离散元对混凝土强度及破坏机理进行研究时,模型中细观参数的选择十分重要。但是在离散元中,细观参数和宏观力学参数(抗压强度、弯拉强度等)无法建立直接联系。通过前文研究发现:对于抗压强度相同的混凝土,其细观参数可能明显不同。因而,为确定合理的细观参数,只能通过大量的数值模拟试验进行标定。标定过程是一个十分复杂的过程,本节在前文研究的基础上,进行大量的抗压强度数值模拟试验,并参考相应文献[3-4],给出不同强度下混凝土细观参数标定值(集料的模量取20 GPa[4]),见表 2。
| 强度等级 | 颗粒参数 | 平行黏结模型参数 | ||||||
| 孔隙率 | 密度/(kg·m-3) | 摩擦系数 | 法向刚度/(×1012N·m-1) | 切向刚度/(×1012N·m-1) | 黏结半径 | 切向强度/(×108 Pa·m-1) | 法向强度/(×108 Pa·m-1) | |
| 7.5 | 0.14 | 2 400 | 0.4 | 3.0 | 3.0 | 0.2 | 2.0 | 2.0 |
| 10 | 0.14 | 2 400 | 0.4 | 3.0 | 3.0 | 0.2 | 3.0 | 3.0 |
| 15 | 0.13 | 2 400 | 0.5 | 4.0 | 4.0 | 0.2 | 4.0 | 4.0 |
| 20 | 0.12 | 2 400 | 0.5 | 5.0 | 5.0 | 0.3 | 5.0 | 5.0 |
| 25 | 0.12 | 2 400 | 0.5 | 5.0 | 5.0 | 0.4 | 5.0 | 5.0 |
| C30 | 0.11 | 2 400 | 0.6 | 6.0 | 6.0 | 0.4 | 5.0 | 5.0 |
| 35 | 0.11 | 2 400 | 0.6 | 6.0 | 6.0 | 0.4 | 6.0 | 6.0 |
| 40 | 0.10 | 2 400 | 0.6 | 6.0 | 6.0 | 0.5 | 6.0 | 6.0 |
| C45 | 0.10 | 2 400 | 0.7 | 7.0 | 7.0 | 0.6 | 8.0 | 8.0 |
| 50 | 0.08 | 2 400 | 0.8 | 8.0 | 8.0 | 0.8 | 10.0 | 10.0 |
| C55 | 0.08 | 2 400 | 0.8 | 8.0 | 8.0 | 0.9 | 12.0 | 12.0 |
| C60 | 0.08 | 2 400 | 0.8 | 8.0 | 8.0 | 1.0 | 14.0 | 14.0 |
3 弯拉强度细观模拟试验 3.1 模型的建立
弯拉强度是水泥混凝土路面设计时的主要设计指标,本节将在第2节抗压强度数值模拟试验研究的基础上,进行弯拉强度数值模拟试验。试验中,试件的生成及细观参数与前文相同,试件长和高分别为40 cm和10 cm,采用墙体加载的方式对试件进行加载,建立模型见图 10,待模型达到平衡后方可进行弯拉强度试验。

|
| 图 10 弯拉强度细观模拟试验模型 Fig. 10 Simulation model for flexural-tensile strength test in meso-scale |
| |
3.2 试验结果及分析
运用控制墙体位移的方式对建立模型进行加载,计算所得应力-应变曲线见图 11。由图 11可以发现,随着加载墙体位移的增加,试件承受应力逐渐增加,当达到弯拉强度时,试件承受应力迅速降低,试件发生破坏,所得模拟试件的弯拉强度为4.89 MPa。由第2节可知,相同细观参数条件下模拟所得抗压强度为38.0 MPa。根据第1节室内试验可知:对于抗压强度为38.7 MPa的混凝土,其弯拉强度为4.76 MPa,数值模拟中抗压强度为38.0 MPa的混凝土弯拉强度为4.89 MPa,可见数值模拟结果与实际情况基本相符。

|
| 图 11 弯拉强度试验结果 Fig. 11 Result of flexural-tensile strength test |
| |
4 抗剪抗压强度细观模拟试验 4.1 模型的建立
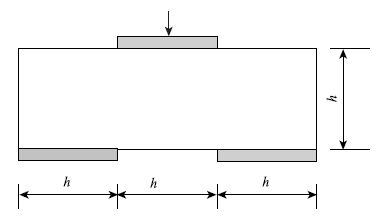
抗剪强度是水泥混凝土的重要力学指标,混凝土的很多破坏形式均与抗剪强度有关,本节在第2节抗压强度研究的基础上,进行抗剪强度数值模拟试验。目前,对于混凝土抗剪强度试验尚无统一标准,常见的有双面直剪试验、矩形梁直接受剪试验及“Z”形试件剪切试验等方法,考虑到试验的可行性,本文采用矩形梁直接受剪试验进行抗剪强度试验。试验中,试件的生成及细观参数与前文相同,试件长和高分别为30 cm和10 cm,采用墙体加载的方式对试件进行加载,加载试件尺寸图见图 12,建立数值模型见图 13,待模型达到平衡后方可进行抗剪强度试验。
|
| 图 12 加载试件尺寸 Fig. 12 Dimensions of loaded sample |
| |

|
| 图 13 抗剪强度细观模拟试验模型 Fig. 13 Simulation model for shear strength test in meso-scale |
| |
4.2 试验结果及分析
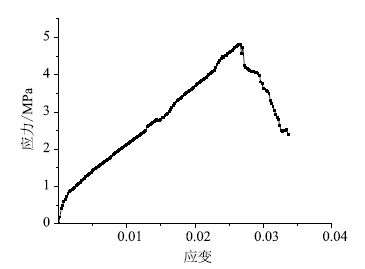
通过控制墙体位移的方式对试件进行加载,计算得到的应力-应变曲线如图 14所示。由图可以看出:随着墙体的不断加载,试件内部应力逐渐增加,当应力达到抗剪强度时,试件内部应力迅速降低,试件发生破坏,可得其抗剪强度为4.81 MPa。由第2节可知,相同细观参数条件下模拟所得抗压强度为38.0 MPa。根据第1节室内试验可知:对于抗压强度为38.7 MPa的混凝土,其抗剪强度为4.69 MPa,数值模拟中抗压强度为38.0 MPa的混凝土抗剪强度为4.81 MPa,可见数值模拟结果与实际情况基本相符。
|
| 图 14 抗剪强度试验结果 Fig. 14 Result of shear strength test |
| |
5 不同强度等级混凝土宏观力学参数推荐值
以表 2中的混凝土细观参数标定值为基础,分别进行抗压强度、弯拉强度和抗剪强度数值模拟试验。考虑到路用混凝土强度较高,仅进行混凝土强度等级在C20以上的相应试验,数值模拟试验结果见表 3。
| 强度等级 | 弹性模量/GPa | 弯拉强度/MPa | 抗剪强度/MPa |
| C20 | 21.8 | 3.11 | 2.57 |
| C25 | 23.9 | 3.43 | 3.01 |
| C30 | 26.2 | 3.92 | 3.62 |
| C35 | 28.4 | 4.36 | 4.17 |
| C40 | 29.8 | 4.95 | 4.85 |
| C45 | 30.8 | 5.19 | 5.07 |
| C50 | 32.0 | 5.63 | 5.39 |
| C55 | 34.9 | 6.01 | 5.71 |
| C60 | 38.1 | 6.57 | 6.08 |
6 结论
(1) 进行抗压强度细观数值模拟试验时,加载到6 000时步时(加载初期),试件内部应力分布较为均匀;加载到20 000时步时,在试件与加载板接触位置开始出现较小的应力集中;加载到30 000时步时,试件开始产生裂缝,试件逐渐破坏;加载到45 000时步时,试件内部产生明显的裂缝,出现明显的滑裂面,试件已经完全破坏。试验可得:混凝土试件的抗压强度为38.0 MPa,其弹性模量为29.4 GPa。
(2) 利用离散元对混凝土抗压强度试验进行数值模拟时,混凝土的抗压强度和弹性模量是多个细观参数综合作用的结果,不同细观参数对其影响程度宜不同;通过细观参数对混凝土抗压强度和弹性模量的影响分析可知:对试件弹性模量影响较大的参数包括摩擦系数、平行黏结刚度和平行黏结半径;对试件抗压强度影响较大的参数包括平行黏结强度、平行黏结半径和摩擦系数。
(3) 对混凝土进行弯拉强度和抗剪强度数值模拟试验,可知:随着加载墙体位移的增加,模拟试件所承受的应力逐渐增加,当试件达到其弯拉强度或抗剪强度时,其内部应力迅速降低,试件逐渐破坏;抗压强度为38.0 MPa的混凝土的弯拉强度和抗剪强度分别为4.89 MPa和4.81 MPa。
将数值试验模拟结果与室内试验结果进行对比,试验结果基本吻合,可见运用离散元对混凝土抗压强度、弯拉强度和抗剪强度进行数值模拟,对混凝土的破坏过程及强度形成机理进行研究是十分可行的。但由于论文建立的模型为二维模型,与三维实体存在一定的区别,建议在未来的研究中建立三维模型,从而对混凝土的破坏及强度形成机理进行研究。
| [1] | YOU Z, BUTTLAR W G. Discrete Element Modeling to Predict the Modulus of Asphalt Concrete Mixtures[J]. Journal of Materials in Civil Engineering , 2004, 16 (2) : 140-146 |
| [2] | ABBAS A R. Simulation of the Micromechanical Behavior of Asphalt Mixtures Using the Discrete Element Method[D]. Pullman:Washington State University, 2004. |
| [3] | LIU Y, YOU Z, DAI Q, et al. Review of Advances in Understanding Impacts of Mix Composition Characteristics on Asphalt Concrete (AC) Mechanics[J]. International Journal of Pavement Engineering , 2011, 12 (4) : 385-405 |
| [4] | LIU Y, DAI Q, YOU Z. Viscoelastic Model for Discrete Element Simulation of Asphalt Mixtures[J]. Journal of Engineering Mechanics , 2009, 135 (4) : 324-333 |
| [5] | YOU Z, LIU Y, DAI Q. Three-dimensional Microstructural-based Discrete Element Viscoelastic Modeling of Creep Compliance Tests for Asphalt Mixtures[J]. Journal of Materials in Civil Engineering , 2010, 23 (1) : 79-87 |
| [6] | 王江洋, 钱振东, 汪林兵. 沥青混合料裂纹发展过程的颗粒流模拟[J]. 公路交通科技 , 2015, 32 (3) : 7-13 WANG Jiang-yang, QIAN Zhen-dong, WANG Lin-bing. Particle Flow Simulation of Crack Development in Asphalt Mixture[J]. Journal of Highway and Transportation Research and Development , 2015, 32 (3) : 7-13 |
| [7] | 冯师蓉, 胡霞光, 刘玉. 粘弹性材料的离散元数值分析[J]. 公路交通科技 , 2008, 25 (2) : 12-15 FENG Shi-rong, HU Xia-guang, LIU Yu. Numerical Analysis of Viscoelastic Materials Based on Discrete Element Method[J]. Journal of Highway and Transportation Research and Development , 2008, 25 (2) : 12-15 |
| [8] | 张东, 黄晓明, 田飞. 级配碎石动三轴试验离散元模拟[J]. 公路交通科技 , 2014, 31 (12) : 39-42 ZHANG Dong, HUANG Xiao-ming, TIAN Fei. Simulation of Dynamic Triaxial Test of Graded Crushed Stone by Discrete Element Method[J]. Journal of Highway and Transportation Research and Development , 2014, 31 (12) : 39-42 |
| [9] | 车法, 陈拴发, 李增宏, 等. 荷载作用下沥青路面表面开裂的扩展[J]. 公路交通科技 , 2010, 27 (5) : 26-29 CHE Fa, CHEN Shuan-fa, LI Zeng-hong, et al. Analysis of Cracks Propagation on Asphalt Pavement Surface under Load[J]. Journal of Highway and Transportation Research and Development , 2010, 27 (5) : 26-29 |
| [10] | 郭红兵, 陈拴发. 开级配大粒径沥青碎石混合料劈裂试验的离散元数值分析[J]. 公路交通科技 , 2014, 31 (11) : 22-26 GUO Hong-bing, CHEN Shuan-fa. Numerical Analysis on Splitting Test of Open-graded Large Stone Asphalt Mixture Using Discrete Element Method[J]. Journal of Highway and Transportation Research and Development , 2014, 31 (11) : 22-26 |
| [11] | 李蕊, 常明丰, 李彦伟, 等. 沥青混合料裂缝扩展过程细观力学模拟[J]. 交通运输工程学报 , 2011, 11 (6) : 1-9 LI Rui, CHANG Ming-feng, LI Yang-wei, et al. Mesomechanics Simulation of Micro-crack Extension Process for Asphalt Mixture[J]. Journal of Traffic and Transportation Engineering , 2011, 11 (6) : 1-9 |
| [12] | 曲立洁, 张德才. 沥青路面级配碎石层应力消散的细观研究[J]. 公路交通科技 , 2014, 31 (9) : 13-17 QU Li-jie, ZHANG De-cai. Microscopic Study on Stress Dissipation in Graded Crushed Stone Layer of Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development , 2014, 31 (9) : 13-17 |
| [13] | 田莉, 刘玉, 王秉纲. 沥青混合料三维离散元模型及其重构技术[J]. 长安大学学报:自然科学版 , 2007, 27 (4) : 23-27 TIAN Li, LIU Yu, WANG Bing-gang. 3D DEM Model and Digital Restructure Technique for Asphalt Mixture Simulation[J]. Journal of Chang'an University:Natural Science Edition , 2007, 27 (4) : 23-27 |
 2016, Vol. 33
2016, Vol. 33
