扩展功能
文章信息
- 姜燕宁, 郝书池
- JIANG Yan-ning, HAO Shu-chi
- 基于部分跨级和集中存储模式的库存配置与选址决策模型
- Inventory Allocation and Location Decision Model Based on Partial Cross-level and Centralized Storage
- 公路交通科技, 2016, 33(11): 152-158
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 152-158
- 10.3969/j.issn.1002-0268.2016.11.023
-
文章历史
- 收稿日期: 2016-01-14
2. 广州城市职业学院, 广东 广州 510405
2. Guangzhou City Polytechnic, Guangzhou Guangdong 510405, China
选址决策属于战略层面,传统的设施选址模型则关注选址成本的最小化,未对选址如何影响运输成本、如何影响库存决策进行深入研究。库存决策属于战术层面,传统的库存模型一般都是假设设施布局为已知条件,不考虑设施选址的差异性而带来的设施建设成本、运输成本及缺货成本的变化,也不考虑库存配置模式对选址策略的影响,没有达到系统整体优化。
集中库存策略为了减少标准差或变异系数的变异性,进行跨越地点将需求进行聚集;在聚集过程中,不同的市场需求被彼此平衡,从而降低需求的变异性,最终导致安全库存及系统总成本降低。G D Eppen[1]分析各点需求为正态分布,且具有相同的线性持有成本和惩罚成本的多点报童模型,得到集中后的模型库存期望成本比分散要低。这种现象称为“风险分摊效应(Risk pooling effect)”,随后国内外学者从不同角度对集中存储问题进行了研究。P L Chang, C T Lin[2]在Eppen模型的基础上考虑运输成本,探讨了3个成本方程为凹和线性情况下集中和分散库存策略的成本关系。M Cherikh[3]对比过量需求一定比例或者全部可以从其他有库存的点获得满足的情况,计算集中和分散库存策略下的期望利润。解琨, 刘凯[4]研究提前期和需求的不确定对安全库存的影响,并通过实例对比集中库存系统和分散库存系统的差异性。邓佩, 张俊婧, 苏翔等[5]用数值分析的方法探讨空间聚集效应下,需求的相关系数变化时对安全库存的影响,并通过实例证明集中存储的安全库存量更低。宋殿辉,苗壮[6]首先探讨需求独立情况下集中储存对安全库存的影响机理,并得出平方根定律;然后通过一个算例发现随着需求相关性的增大,分散模式与集中模式总安全库存之间的差距在缩小。逄兆勇[7]研究集中存储和分散存储的期望库存成本和利润,并探讨市场需求相关性和需求变异系数对风险分摊效应的影响。O Berman, D Krass, M Mahdi Tajbakhsh[8]研究绝对成本、相对成本与需求变化和共享地数目的敏感性,研究表明,在需求变异系数水平较低的情况下,随着需求变化在一定范围内的增加,共享的绝对利益增加、相对利益保持不变,但当变异水平较高时,风险分摊效应下降。
随着研究的深入,越来越多的研究者开始在选址模型中考虑风险分摊效应,将选址成本和库存成本集中考虑。C Das, R Tyagi[9]结合运输成本和库存成本,根据集中存储程度,探讨了5种不同的存储策略。P A Miranda, R A Garrido[10]研究发现集中存储效益受到单位持有成本和需求变化的影响,并构建了考虑风险分摊效应的库存-选址模型。陈兴[11]构建集中存储的多级库存控制系统,分别构建集中存储和分散存储的库存管理模型。娄山佐,吴耀华[12]利用分解协调法解决多库房库存-路径问题。N Vidyarthi, E Çelebi, S Elhedhli等[13]探讨安全库存集中存储的表达式,并构建生产、库存和配送整合系统模型。L Ozsen, C R Coullard, M S Daskin[14]假设以最大需求作为配送中心容量限额,其各个配送中心集中存放安全库存,构建了选址-库存模型。S Park, T E Lee, C S Sung[15]考虑风险分摊效应,并假设各项成本受到提前期的影响来构建模型。Z Firoozi, S H Tang, S Ariafar等[16]考虑风险分摊效应对安全库存的影响,构建包括采购成本、库存成本、运输成本和订货成本的总体模型。
然而已有研究成果对于单级集中存储问题研究较多,也有很多成功的实例,但是多级供应链中的集中存储问题缺乏研究,即需要考虑供应链多个层级都允许同级间集中存储安全库存。另外,现有研究假设配送中心级和需求级各自集中存储自己本阶段的安全库存,如果考虑配送中心与需求点间的距离、紧急调运成本的影响,此策略是否为最优策略值得探讨,部分跨级存储策略也许是一种新的降低系统安全库存的方法。部分跨级存储可以表述为:配送中心级的安全库存一部分存放在本级,另一部分转移存放在需求级;需求级的安全库存也可以同样决策。因此,在上述联合库存-选址模型中将配送中心级和需求级集中存储组的划分、最优跨级存储比例系数作为模型的决策变量更为合理,同时也能够更好地反映实际情形。基于以上考虑,本文在一般的联合库存-选址模型的基础上将集中存储组的划分和最优跨级存储比例系数作为模型的决策变量,以系统总成本最低为目标函数,建立随机需求下的联合选址-库存模型,并给出一种求解模型的启发式算法。
1 问题描述与研究背景(1) 问题描述与假设
本文研究的问题可以描述如下:给定需求点的集合J以及备选的配送中心集合I,每个需求点的需求服从正态分布,需求解决的问题是:①如何确定在哪些备选配送中心处建立配送中心;②如何确定每个配送中心为哪些需求点提供服务;③需求级和配送中心级的可以分为几个集中存储组,选择每个集中存储组中哪个点为本组集中存储点;④如何确定跨级存储的最优比例,从而使系统总成本最低。如图 1所示。
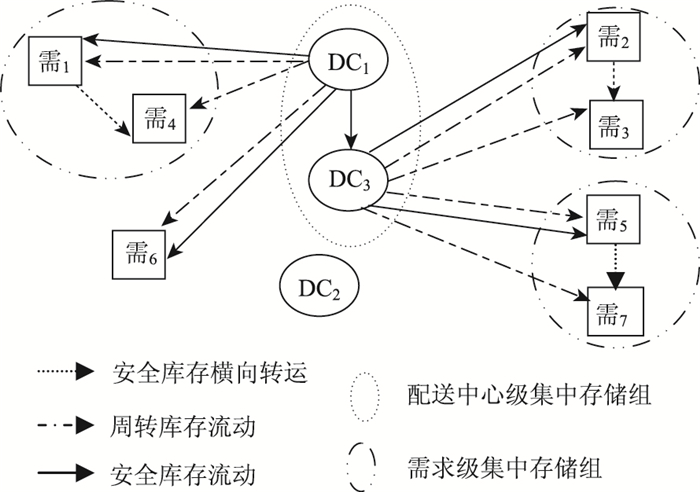
|
| 图 1 多级供应链安全库 Fig. 1 Multi-echelon supply chain safety inventory centralized storage mode |
| |
模型假定如下:①一个配送中心可以向多个需求点供货,但是一个需求点只能由一个配送中心进行配送;②(Q, R)库存检查策略,配送中心无容量约束;③各需求点的需求完全独立且均服从正态分布;④不计安全库存的横向转运时间。
(2) 模型参数与决策变量
①模型参数:
I为备选配送中心i的集合; J为需求点j的集合; K为库存安全系数;uj为需求点j每天需求量均值;σj为需求点j每天需求量标准差; ui为配送中心i每天需求量均值; σi为配送中心i每天需求量标准差; Lj为需求点j提前期均值; σLj为需求点j提前期标准差; Li为配送中心i提前期均值; σLi为配送中心i提前期标准差; S为每次订购成本; h为单位库存持有成本; C0为从供应商到配送中心的单位运输成本; C1为从配送中心到需求点的单位运输成本; C2为单位横向转运成本; C3为配送中心单位产品建设成本; C4为单位缺货成本; gi为配送中心i固定建设成本; α为配送中心级的库存放入需求级的比例系数,0≤α≤1; β为需求级的库存放入配送中心级的比例系数,0≤β≤1; di为供应商到配送中心i的距离; dij为配送中心i到需求点j的距离; dmv为配送中心级集中存储点m到同组其他非集中存储点v的距离; dpw为需求级集中存储点p到同组其他非集中存储点w的距离; λ为年运营天数,取300 d。
②决策变量
Xi为0,1变量,如果配送中心选在i位置,取1,否则取0;Xij为0,1变量,如果需求点j由配送中心i服务,取1,否则取0;Xim为0,1变量,在已选定的配送中心(Xi=1)中选择m(m∈i)作为配送中心级安全库存集中存储点时取1,否则取0;Ximv为0,1变量,当配送中心m为配送中心v(v∈i且v≠m)提供安全库存横向转运时取1,否则取0;Xijp为0,1变量,选择需求点p(p∈j且Xi=1, Xij=1)为需求级安全库存集中存储点时取1,否则取0;Xijpw为0,1变量,表示需求点p(p∈j)为同组的需求点w(w∈j且w≠p)提供安全库存横向转运时取1,否则取0。
2 模型构建(1) 配送中心建设成本
配送中心的均值和标准差与下级需求点的需求相关,而需求级每个集中存储组的标准差σTp=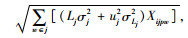
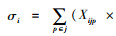
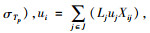
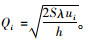
考虑配送中心建设成本与其容量相关,而容量大小取决于经济订购批量和安全库存量之和,配送中心i的建设成本为:Fi=gi+C3×[Qi+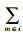
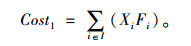
|
(1) |
(2) 运输成本
从配送中心i到需求点j的运输成本为Tij=C1×λ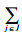
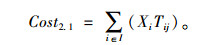
|
(2) |
配送中心i的总需求量λui,从供应商到配送中心i的运输成本为Ti=C0×di×λui,配送中心级总的运输成本:
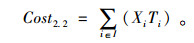
|
(3) |
(3) 周转库存成本
需求点j的周转库存量为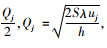
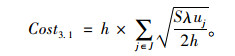
|
(4) |
配送中心i的周转库存量为
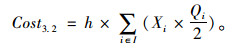
|
(5) |
(4) 安全库存成本
若不考虑跨级存储情况,安全库存只存放于各级的集中存储点,配送中心级每个集中存储组的标准差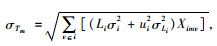
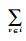
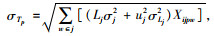
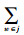
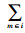
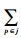
若考虑跨级存储情况,需求级上级存储的安全库存计算到对应的集中存储点配送中心m上,配送中心下级存储的安全库存按比例分配给其负责配送的需求级的集中存储点p上。
配送中心m的安全库存为SSm=(1-α)×K×σTm+β×K×Ximv×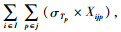
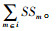
需求点p的安全库存为SSp=α×K×σTm×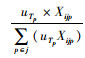
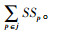
则总安全库存成本:
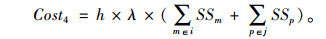
|
(6) |
(5) 横向转运成本
由于转运量等于各个非集中存储点的缺货量,转运距离为集中存储点到各个非集中存储点的距离。所以:
非集中存储需求点j的订货点:Rj=Ljuj,需求点j的期望缺货量为: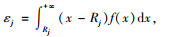
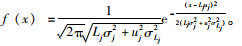
需求级总转运成本:
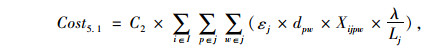
|
(7) |
式中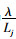
非集中存储点的配送中心i的订货点Ri=Liui,配送中心i的期望缺货量为: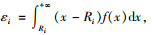
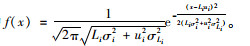
所以,配送中心级总转运成本:
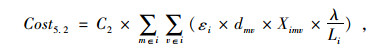
|
(8) |
式中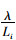
(6) 缺货成本
由于非集中存储点的缺货由集中存储点通过横向转运瞬间到达,所以仅考虑集中存储点的缺货成本。
集中存储组p的订购点Rp=Lp×uTp+SSp,期望缺货量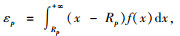
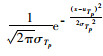
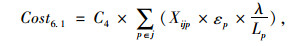
|
(9) |
式中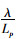
集中存储组m的订购点Rm=Lm×uTm+SSm,期望缺货量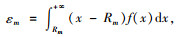
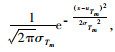
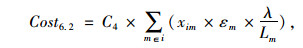
|
(10) |
式中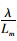
(7) 总成本模型
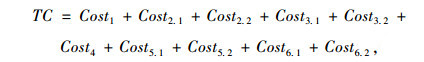
|
(11) |
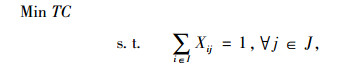
|
(12) |
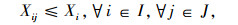
|
(13) |
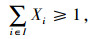
|
(14) |
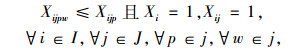
|
(15) |
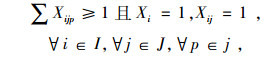
|
(16) |
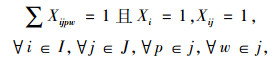
|
(17) |
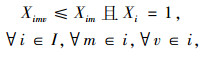
|
(18) |
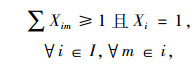
|
(19) |
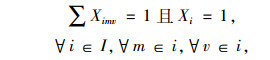
|
(20) |

|
(21) |
式(12)表示每个需求点仅有一个配送中心为其配送;式(13)表示只有选定的配送中心才能为需求点服务式(14)表示至少在备选点中选择一个作为配送中心;式(15)表示只有选定作为集中存储点的需求点才能为其他需求点提供横向转运;式(16)表示至少选择一个需求点作为安全库存的集中存储点;式(17)表示在需求级,每个非集中储存点仅有一个集中存储点为其提供横向转运;式(18)表示只有选定作为集中存储点的配送中心才能为其他配送中心提供横向转运;式(19)表示至少选择一个配送中心作为安全库存的集中存储点;式(20)表示在配送中心级,每个非集中存储点仅有一个集中存储点为其提供横向转运;式(21)表示只能选择一个方向进行跨级存储。
3 算法设计与数值算例 3.1 算例参数现有1个供应商、5个备选配送中心(i=1,2,3,4,5)、20个需求点(j=1,2, …, 20)构成的配送网络,K=1.28,S=8 000元/次,C0=0.1元/(t·km),C1=0.28元/(t·km),C2=0.5元/(t·km),C3=10元/t,C4=15元/t,h=12元/(t·d),λ=300 d,α, β变动。其他数据如表 1~表 3所示。
| 参数 | 代号 | |||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| uj/t | 45 | 37 | 29 | 38 | 44 | 57 | 52 | 35 | 28 | 56 | 42 | 48 | 36 | 25 | 22 | 32 | 37 | 41 | 45 | 59 |
| σj/t | 5 | 4 | 6 | 3 | 6 | 6 | 4 | 5 | 7 | 4 | 6 | 7 | 4 | 3 | 5 | 4 | 6 | 7 | 7 | 5 |
| Lj/d | 2 | 3 | 2 | 3 | 2 | 3 | 4 | 1 | 2 | 3 | 2 | 2 | 3 | 2 | 1 | 3 | 2 | 2 | 2 | 3 |
| σLj/d | 0.1 | 0.3 | 0.4 | 0.6 | 0.5 | 0.8 | 1 | 0.1 | 0.3 | 1.2 | 0.8 | 0.7 | 1.3 | 0.5 | 0.2 | 0.7 | 0.4 | 0.3 | 0.2 | 0.5 |
| 参数 | 代号 | ||||
| Li/d | 5 | 7 | 6 | 5 | 4 |
| σLi/d | 1 | 1.2 | 1 | 0.8 | 0.6 |
| gi/元 | 1 200 000 | 870 000 | 960 000 | 1 100 000 | 730 000 |
| 坐标/km | (-5,45) | (-30,10) | (-45,-40) | (-20,-35) | (38,50) |
| 代号 | 坐标 |
| 1 | (-40,10) |
| 2 | (-20,70) |
| 3 | (-42,-32) |
| 4 | (-70,-43) |
| 5 | (-10,-60) |
| 6 | (-40,32) |
| 7 | (-68,10) |
| 8 | (12,15) |
| 9 | (-5,35) |
| 10 | (0,-40) |
| 11 | (-10,-10) |
| 12 | (10,68) |
| 13 | (43,72) |
| 14 | (65,70) |
| 15 | (32,36) |
| 16 | (52,30) |
| 17 | (20,30) |
| 18 | (-8,15) |
| 19 | (-15,-33) |
| 20 | (-15,-72) |
| 注:假设供应商的坐标为(0,0)。 | |
3.2 算法设计
问题为NP-hard问题,利用遗传算法求解,在MATLAB中调用GAOT遗传算法工具箱来进行求解,主要函数及参数设置如下:
startPop=initializega (num, bounds, evalFN, [], [1e-1 1 1]);
[x endPop bPop trace]=ga (bounds, evalFN, [], startPop, [1e-1 1 1], ′maxGenTerm′, [2000], ...
′normGeomSelect′, [0.08], ′simpleXover′, [2 0], ′unifMutation′, [4 0 0])。
(1) 定义变量边界
共有130个变量,前20个变量表示需求点分配给哪个配送中心,取值在1~100.9(边界增加0.9,可以增加“100”的选择机率);第21~120个变量表示需求点级的集中存储点位置,取值在1~40.9之间;第121~125个变量表示配送中心选定情况,取值在1~5.9之间;第126~130个变量表示配送中心级中心存储点的指派情况,取值在1~10.9之间。
(2) 生成一组随机变量A,包含131个随机数,取值分别在各自的边界内;利用fix(A)向零取整,得到一组整数随机变量B。
(3) 需求级需求点的分配及集中存储点的指派情况:
①通过Zeros(20*5, 20+1)生成与初始解相同行和列的零矩阵C。
②对零矩阵C赋值,赋值规则如下:
第2至第21列,每一列需要且仅需要出现一个“1”,表示需求点指派情况,赋值公式为: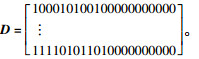
第1列表示集中存储点的选择,若本行从第2列到第21列中有“1”出现,则本行第1个数为“1”;例如某初始解矩阵为
③第1列“1”的指定(采取循环指定方法):
列出每一行“1”的序号(从第2列开始)如D中的第一行为E[4,6,9],并统计每行第2列到第21列的“1”的个数,假设为τ(如D中第一行τ为3)。
为确保E中每个数字循环指定的机率差不多,对矩阵E放大n倍,n=fix(2*需求点个数/τ+1),此例中n等于14,即构成矩阵F=[4,6,9,4,6,9,4,6,9,4,6,9,4,6,9,4,6,9,4,6,9,4,6,9,4,6,9,4,6,9,4,6,9,4,6,9,4,6,9,4,6,9]。
再看B中的第21个变量,假若为“11”,即查找F(11),为“6”。
则D(1,1)的“1”表示第6点为需求级的集中存储点,负责4, ,6,9这3个需求点。
采取同样的方法确定D(2,1),…,D(100,1)中的“1”的位置。
(4) 配送中心级配送中心选择情况:
第1步:首先生成5*5的零矩阵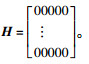
第2步:对零矩阵H赋值,赋值规则如下:
第1至第5列,每一列需要仅需要出现一个“1”(若不列出现“1”表示该配送中心未被选用),表示配送中心的选定情况,赋值公式为:H(B(120+i), i)=1,i=1,…,5;假设B中第121~125变量为3,5,5,2,3,则有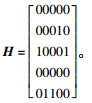
若在初始解D中的第1~20行(对应第1个配送中心)所有的元素和为零,则表示第1个配送中心没有选到,则H中的第1列元素全为零,即等于H(:;1)*0;同样第21~40行对应第2个配送中心,依此类推。
(5) 配送中心级集中存储点的指定方法同上。
3.3 算例计算结果计算α, β取不同值的总成本,然后对比各种跨级存储策略。
由表 4可知:α=0.5,β=0时总成本最低,为最优跨级存储比例;安全库存全部放在配送中心级(α=0,β=1.0)成本最高。最优库存配置方案为选择第2,4,5个配送中心,且第2个配送中心为配送中心级安全库存集中存储点,即配送中心2,4,5的安全库存全部集中存储到配送中心2处。配送中心与需求点的指派关系为:配2[18;1(1, 8);7]、配4[4;19;20(3,5,10,11,20)]、配5[6(6,9,16);2(2,12,13,15);14;17];第2个配送中心负责18,1,8,7这4个需求点的配送,其中“1(1,8)”表示需求点1集中存储需求点1和8的安全库存;其他类同。
| 取值 | 总成本/(×107 CNY yuan) | |
| α | β | |
| 0 | 0 | 1.808 |
| 0 | 0.1 | 1.788 |
| 0 | 0.2 | 1.759 |
| 0 | 0.3 | 1.779 |
| 0 | 0.4 | 1.796 |
| 0 | 0.5 | 1.825 |
| 0 | 0.6 | 1.820 |
| 0 | 0.7 | 1.851 |
| 0 | 0.8 | 1.861 |
| 0 | 0.9 | 1.876 |
| 0 | 1.0 | 1.892 |
| 0.1 | 0 | 1.699 |
| 0.2 | 0 | 1.639 |
| 0.3 | 0 | 1.748 |
| 0.4 | 0 | 1.749 |
| 0.5 | 0 | 1.638 |
| 0.6 | 0 | 1.712 |
| 0.7 | 0 | 1.714 |
| 0.8 | 0 | 1.703 |
| 0.9 | 0 | 1.712 |
| 1.0 | 0 | 1.716 |
3.4 模型的稳定性验证
分别取3组不同规模的随机算例,且在不同的规模下随机取10组值,用这10组值分别求解不同α,β取值下的输出结果,其中库存点位置在数值1~20中随机产生,并向零取整。
由表 5可知:模型在不同的算例规模下有较好的稳定性;且算例规模越大时,部分跨级存储相对于不跨级(α,β=0)存储优势更明显。
| 取值 | 总成本/(×107 CNY yuan) | |||
| α | β | 5个配送中心、20个需求点 | 3个配送中心、15个需求点 | 2个配送中心、12个需求点 |
| 0 | 0 | 1.808 7 | 1.415 0 | 1.253 9 |
| 0.5 | 0 | 1.638 9 | 1.413 1 | 1.250 8 |
4 结论
文章通过构建包含建设成本、运输成本、周转库存成本、安全库存成本、横向转运成本、缺货成本的库存配置与选址决策模型,利用算例以总成本最低为优化目标进行了试验。可以发现:(1) 部分跨级存储库存配置模式是可行的;(2) 在不同算例规模下,呈现同样的规律,这说明模型的稳定性较好;且算例规模越大,部分跨级存储优势越明显;(3) 部分跨级库存的系数α,β的最优取值受到参数的影响,在实际应用中要进行多种组合的比对分析;(4) 在配送中心无容量约束的情况下,假设其建设费用与容量线性相关,而容量大小取决于所服务需求点的分配及安全库存的配置模式,更能合理规划和控制配送中心的建设容量,提高利用率。
| [1] | EPPEN G D. Note-Effects of Centralization on Expected Costs in a Multi-Location Newsboy Problem[J]. Management Science , 1979, 25 (5) : 498-501 |
| [2] | CHANG P L, LIN C T. On the Effect of Centralization on Expected Costs in a Multi-location Newsboy Problem[J]. Journal of the Operational Research Society , 1991, 42 (11) : 1025-1030 |
| [3] | CHERIKH M. On the Effect of Centralisation on Expected Profits in a Multi-location Newsboy Problem[J]. Journal of the Operational Research Society , 2000, 51 (6) : 755-761 |
| [4] | 解琨, 刘凯. 供应链库存管理中的风险问题研究[J]. 中国安全科学学报 , 2003, 13 (5) : 26-29 XIE Kun, LIU Kai. Study on the Risk in Supply Chain Inventory Management[J]. China Safety Science Journal , 2003, 13 (5) : 26-29 |
| [5] | 邓佩, 张俊婧, 苏翔, 等. 空间需求聚集下安全库存模型及其实证[J]. 工业工程与管理 , 2006, 11 (4) : 21-23 DENG Pei, ZHANG Jun-jing, SU Xiang, et al. Research on Safe Stock Model and Its Instance under Agglomerating the Space Requirement[J]. Industrial Engineering and Management , 2006, 11 (4) : 21-23 |
| [6] | 宋殿辉, 苗壮. 集中存储对安全库存影响机理研究[J]. 物流技术 , 2008, 27 (8) : 72-73 SONG Dian-hui, MIAO Zhuang. Impact of Aggregation Stock in Safety Inventory[J]. Logistics Technology , 2008, 27 (8) : 72-73 |
| [7] | 逄兆勇.基于风险分担的供应链库存最优控制策略研究[D].青岛:中国海洋大学, 2009. PANG Zhao-yong. Research on Optimal Inventory Control Strategies Based on Risk Pooling in Supply Chain[D]. Qingdao:Ocean University of China, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10423-2009172050.htm |
| [8] | BERMAN O, KRASS D, MAHDI TAJBAKHSH M. On the Benefits of Risk Pooling in Inventory Management[J]. Production and Operations Management , 2011, 20 (1) : 57-71 |
| [9] | DAS C, TYAGI R. Role of Inventory and Transportation Costs in Determining the Optimal Degree of Centralization[J]. Transportation Research Part E:Logistics and Transportation Review , 1997, 33 (3) : 171-179 |
| [10] | MIRANDA P A, GARRIDO R A. Incorporating Inventory Control Decisions into a Strategic Distribution Network Design Model with Stochastic Demand[J]. Transportation Research Part E:Logistics and Transportation Review , 2004, 40 (3) : 183-207 |
| [11] | 陈兴.采用多级库存管理的城市配送中心选址研究[D].长沙:长沙理工大学, 2007. CHEN Xing. Research on City Distribution Centers Location with Multi-echelon Inventory Management[D].Changsha:Changsha University Science & Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10536-2007205920.htm |
| [12] | 娄山佐, 吴耀华. 基于分解协调法解决多库房库存-路径问题[J]. 公路交通科技 , 2007, 24 (9) : 145-148, 158 LOU Shan-zuo, WU Yao-hua. Solving Multi-depot Inventory-routing Problems Based on Decomposition and Coordination Method[J]. Journal of Highway and Transportation Research and Development , 2007, 24 (9) : 145-148, 158 |
| [13] | VIDYARTHI N, ÇELEBI E, ELHEDHLI S, et al. Integrated Production-inventory-distribution System Design with Risk Pooling:Model Formulation and Heuristic Solution[J]. Transportation Science , 2007, 41 (3) : 392-408 |
| [14] | OZSEN L, COULLARD C R, DASKIN M S. Capacitated Warehouse Location Model with Risk Pooling[J]. Naval Research Logistics , 2008, 55 (4) : 295-312 |
| [15] | PARK S, LEE T E, SUNG S S. A Three-level Supply Chain Network Design Model with Risk-pooling and Lead Times[J]. Transportation Research Part E:Logistics and Transportation Review , 2010, 46 (5) : 563-581 |
| [16] | FIROOZI Z, TANG S H, ARIAFAR S, et al. An Optimization Approach for A Joint Location Inventory Model Considering Quantity Discount Policy[J]. Arabian Journal for Science and Engineering , 2013, 38 (4) : 983-991 |
 2016, Vol. 33
2016, Vol. 33
