扩展功能
文章信息
- 李娟, 曲大义, 刘聪, 王进展, 许翔华
- LI Juan, QU Da-yi, LIU Cong, WANG Jin-zhan, XU Xiang-hua
- 基于元胞自动机的车辆换道行为研究
- Study on Vehicle Lane-changing Behavior Based on Cellular Automaton
- 公路交通科技, 2016, 33(11): 140-145
- Journal of Highway and Transportation Research and Denelopment, 2016, 33(11): 140-145
- 10.3969/j.issn.1002-0268.2016.11.021
-
文章历史
- 收稿日期: 2016-03-04
换道行为是车辆驾驶过程中常见的行为之一,车辆换道行驶对道路交通流的影响较大。近几十年来,国内外交通学者从不同角度对车辆换道行为进行了研究分析,从宏观方面和微观方面建立了许多交通流理论和模型,其中元胞自动机理论被较多地应用到交通领域,尤其是对于车辆驾驶行为的研究。元胞自动机交通流模型结构简单,能很好地描述交通流这类非线性现象。
元胞自动机模型简称CA模型,其实质是在一个具有离散、有限状态的元胞组成的元胞空间上,按照一定的局部规则,在离散的时间维度上演化的动力学系统[1]。CA模型包括4个部分:元胞、元胞空间、邻域及更新规则。元胞自动机模型最早由Cremer等[2]提出;一维模型由Wolfram[3]命名为184号模型;Nagel等[4]提出了NS模型;Nagatani[5]在184模型的基础上提出了双车道模型;Daoudia等[6]提出三车道CA模型;刘友军等进行了基于元胞自动机的强制换道模型研究[7];史丹丹等[8]考虑车-车通信建立了双车道的元胞自动机交通流模型;杨海飞等[9]从宏观运动波和微观元胞自动机两个方面进行了交通流混合建模;王江锋等[10]基于元胞自动机建立了改进的多车道换道模型;施俊庆等[11]对元胞自动机模型在城市路网中的应用进行了归纳整理。
上述元胞自动机理论的应用都局限于一种换道方式的研究,没有针对换道的不同方式进行建模分析并对比不同换道方式对交通流的影响。本文基于元胞自动机理论,对车辆不同换道方式进行建模分析,旨在通过对换道过程的研究,在提高交通效率、降低交通事故、保障交通安全等方面有很好的应用价值。
1 换道行为分析车辆在直行道路上的行驶过程中,主要涉及的驾驶行为就是换道,在换道过程中,较常产生车辆之间的交通事故,交通安全性成为考虑的重点问题。典型的换道行为过程主要包括感知、判断、操作3个阶段。驾驶员首先在感知到周围环境信息的情况下,对得到的信息进行分析处理后做出相应判断,然后通过对车辆进行操作来改变车辆运动状态并达到驾驶操作的目的。在多车道道路上,车辆换道行为较多发生,影响车辆换道行为的因素需要考虑其所在车道车辆和相邻车道车辆。
传统换道类型的分类方法主要是以驾驶员的换道需求为前提,将其分为判断性换道和强制性换道[12]。后来的换道行为研究中,交通学者将车辆换道类型分为自由换道、强制换道、协作换道3种[13]。
(1) 自由换道:目标车道上跟随车与前导车之间的相对间距没有明显变化,换道过程中换道车与其周边车辆之间基本不会产生干扰。
(2) 强制换道:换道车强制汇入目标车道,目标车道跟随车被迫减速。
(3) 协作换道:换道车发出换道信号,目标车道跟随车主动减速协助换道车成功换道。
上述3种换道方式的主要区别在于换道车和跟随车相互作用的效果。在自由换道中车辆间几乎没有任何影响。在强制性换道中,换道车通过建立相互关系起主导作用,而跟随车只能以减速来应对。在协作换道中,交互行为主要由3部分组成:首先,换道车表明换道需求;然后,跟随车接收换道信号,主动减速为换道车创造更大换道空间;最后,两车相对间距满足安全间距要求,换道车执行换道操作。
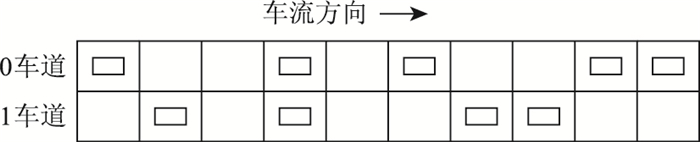
2 建立换道模型 2.1 双车道环境模型将双车道道路视为两条由n个元胞组成的离散格点图,如图 1所示。
|
| 图 1 双车道元胞自动机模型 Fig. 1 A two-lane cellular automaton model |
| |
设元胞长为l;车辆长为lc;Cn为第n辆车所在车道,Cn=1或0;Vi(t)为第i辆车在t时刻的速度;Xi(t)为第i辆车车尾在t时刻的位置;gapi, i+1(t)为两车行驶间距, 其初始值为第i辆车车头与第i+1辆车车尾之间的距离[gapi, i+1(t)=Xi+1(t)-Xi(t)-lc];Vmax为车辆的最大速度;amax为车辆最大加速度。
传统的STCA模型建立了符合现实交通流状态的双车道换道规则,即:
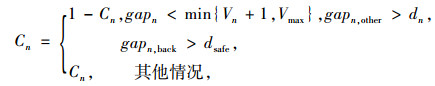
|
(1) |
式中,gapn,gapn, other,gapn, back分别为第n辆车与前方车辆的间距、与相邻车道前方车辆的间距、与相邻车道后方车辆的间距;dsafe为模型中限定的安全换道间距,在STCA模型中dsafe=Vmax;Cn为第n辆车所在车道,且Cn=1或0。gapn < min{Vn+1, Vmax}表示第n辆车在原车道受到阻挡;gapn, other>dn表示该受阻车辆可以在另一车道上达到更快的速度;gapn, back>dsafe表示如果换道,安全换道间距符合条件,即在另一条车道上,后方的车辆与其有一定距离。在STCA模型中,对车辆设置的换道规则是单一不变的,无法再现实际交通的多样性。
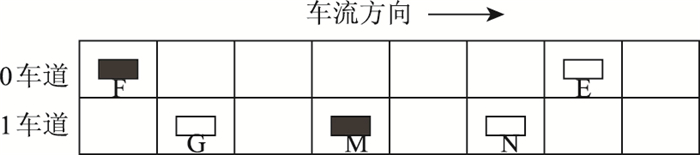
2.2 模型建立在对换道行为研究过程中简化模型,只考虑目标车辆相邻车道前、后车对换道的影响,如图 2所示。Vf和Vm分别为目标车道后车F和换道车辆M的速度;af和am分别为车辆F和车辆M的随机加速度。
|
| 图 2 车辆之间相互位置关系 Fig. 2 Location relationship of vehicles |
| |
当gapme(t)>gapmn(t)且gapmn(t) < min{Vm+am, Vmax}时,说明M车在原车道受到阻挡,换道到相邻车道能够获得更快的速度,此时车辆为避免减速亟待换道,其中gapme表示M车和E车的车间距,gapmn表示M车和N车的车间距。车辆换道需满足两个条件:一是速度空间优势,车辆在本车道无法按照期望速度行驶,且此时相邻车道行驶条件较好;二是换道安全条件,意为车辆换道需要满足一定的安全间距,避免交通事故。需要考察F车对M车的影响。当M车换道过程时,M车与F车车易发生侧面碰撞和刮擦,当M车驶入目标车道时,F车与M车易发生追尾。为避免交通事故发生,保证行车安全,车辆换道临界条件的判定是必要环节。不同类型的换道方式对F车行驶状态产生不同影响,本文将利用元胞自动机对3种换道方式进行建模解析。
2.2.1 自由换道M车可以自由换道,即M车换道驶入目标车道,对F车没有影响,F车可以恒定速度行驶,M车运行状态的改变对道路整体运行态势不产生扰动。M车换道一般分为纵向恒速和纵向恒定加速两种方式,车辆安全换道要满足需求安全间距dsafe,由国内外研究可知,需求安全间距主要由两车相对纵向速度和相对纵向加速度及时间决定。当gapfm>dsafe时,车辆可以自由换道不受约束,其中gapfm表示F车和M车的车间距。
(1) M车恒定速度换道
速度更新:
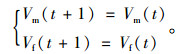
|
(2) |
位置更新:
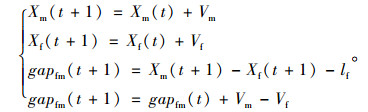
|
(3) |
当Vm>Vf时,gapfm递增,gapfm>dsafe≥0恒成立,自由换道条件符合;当Vm < Vf时,gapfm递减,M车需在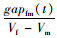
(2) M车恒定加速度换道
速度更新:
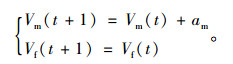
|
(4) |
位置更新:
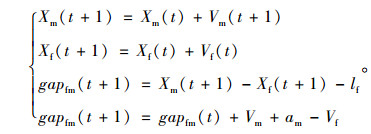
|
(5) |
当Vm < Vf时,M车进行加速换道直到进入目标车道后满足Vm=Vf,随后进行速度为Vf的恒速运动,保证该车道车流运行稳定性。ts为车辆进行加速操作到换道成功所需时间,则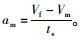
M车发出换道信号后,不顾及F车的运行状态直接执行换道操作。当M车进行强制换道时,在不发生冲突的前提下,F车需以最大减速度进行减速运动,以保证行驶过程中gapfm总满足换道安全间距。
车辆换道安全间距为:
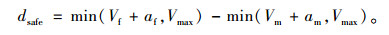
|
(6) |
式(6)表示在下一时刻相邻车道后车F的最大可能速度减去本车M的最大可能速度。车辆强制换道大体有以下几种影响因素:车辆前方出现障碍物或交通限制;前方为匝道尽头;濒近交叉口实线有转向需求;驾驶员亢进性强等。前面几种因素可以分析得到,车辆离最迟换道位置距离越近,越容易发生强制换道,用换道压力α来定义。驾驶员亢进性体现了驾驶员的类型,在换道过程中,驾驶员亢进性越强,越容易发生强制换道,定义亢进系数为β,β越大,强制换道的可能性越大。
根据交通标志设置中识别距离的要求,在离换道位置为50 m处设置标志牌,假设此时换道压力为1,l为距最迟换道位置的距离[14],则:
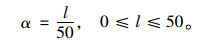
|
(7) |
假设强制换道可行度γ取决于两车间距、换道压力、驾驶员亢进性和两车相对速度及加速度等,则:
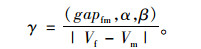
|
(8) |
参考文献[15]可知,γ>1.4时换道安全。M车强制换道时,F车以最大减速度amax减速运动。
速度更新:
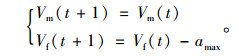
|
(9) |
位置更新:
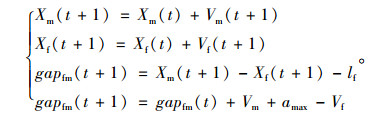
|
(10) |
M车有换道意向,在打开转向灯的同时,不是直接进行换道操作,而是以恒定速度Vm匀速前进,然后观察目标车道后车F的反应,此时F车一般有两种决策可能:允许M车换道请求,以一定的减速度做减速运动为M车换道提供足够的安全间距,M车顺利换道;不接受其换道请求,加速或恒速前进,M车只能等待下一次换道机会。这体现了车辆之间的协作关系,存在着车辆间动态信息的交换。
协作换道过程变化主要受到后车F决策结果的影响,F车以p1概率加速前进,以p2概率减速前进,p1+p2=1。加、减速概率主要受到驾驶员类型的影响(分别对应激进型,保守型)。
(1) 车辆F加速前进。Vf→min (Vf+af, Vmax),Vm=Vm,gapfm递减,换道间距更加不符合要求,M车只能放弃换道。
(2) 车辆F减速前进。F车通过t1时间的减速运动,使gapfm(t1)满足两车换道安全间距。
速度更新:
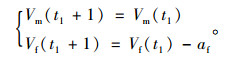
|
(11) |
位置更新:
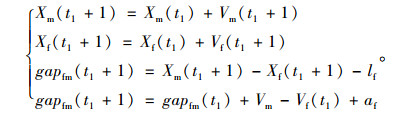
|
(12) |
对上述模型进行模拟仿真分析,由于自由换道不受约束,所以不进行模拟。将STCA模型与本文强制换道和自由换道两种模型进行对比分析。仿真元胞如图 2所示。车道1为换道车所在车道,车道0为换道车目标车道,两条车道均由1 000个元胞组成,总长7.5 km。设置车辆速度为5个元胞单位,车辆按照密度ρ0随机分布在两条离散元胞链上,随机慢化率p=0.25。每次运行1 800个时间步,为消除暂态影响,前后450个时间步不进行统计,只考虑中间900个时间步(15 min)的交通流数据。pm表示换道成功率,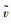
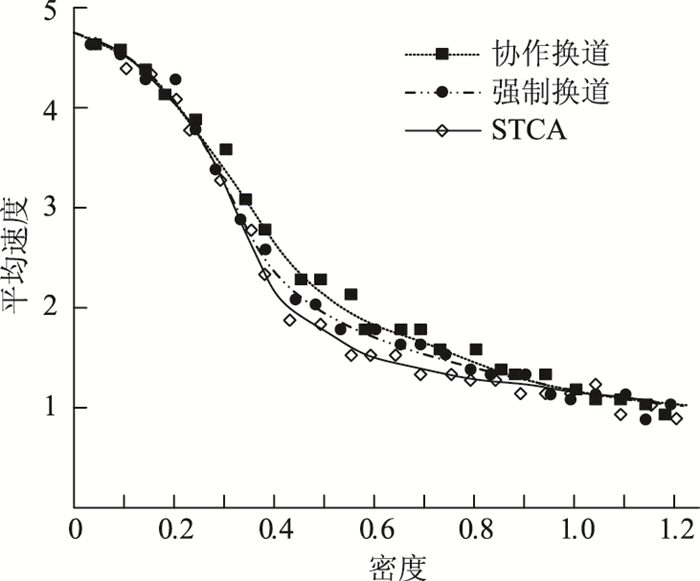
改变车辆密度,观察车辆平均速度的变化。通过仿真得到结果如图 3所示。
|
| 图 3 平均速度与车辆密度的关系 Fig. 3 Relationship between average speed and vehicle density 注:横坐标为密度,表示车辆总数占总元胞的比例,单位为车辆数/元胞数;纵坐标为平均速度,单位为元胞数/时间步,下同。 |
| |
由图 3可以看出,3种模型在相同的密度情况下,当交通流密度较低时,车辆满足自由换道条件,车流速度变化不大,3种模型优劣势不明显。随着密度增大,车辆行驶受到周围环境车辆的影响速度降低,为寻求速度优势,换道期望增加。数据表明,车辆在进行协作换道时,比直接进行强制换道获得的平均速度要高,依照本文模型进行强制换道,又比STCA模型下换道获得的平均速度要高。当密度达到一定程度后,模型的优势不再明显,车流呈现阻塞相,车辆行驶速度迟缓。对比可知,在进行车车之间的信息交互后协作换道,能够提高车辆平均速度,使道路资源得到较为充分的利用。
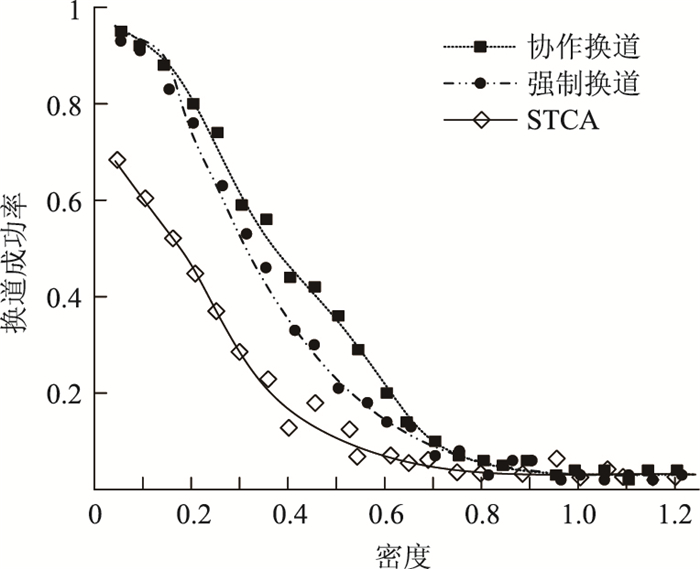
3.2 换道成功率分析改变车辆密度,观察车辆换道成功率的变化,仿真结果如图 4所示。在密度较小时,道路资源相当充裕,车辆换道成功率很大,3种模型的优势体现不出来。随着密度增大,车辆换道变得困难,通过车辆协作换道,成功率明显高于强制换道,模型优势得到体现。但在高密度情况下,车辆换道困难,车流拥挤,换道成功率极低,符合实际情况。其中,STCA模型换道规则中的安全间距为后车的最大速度,在提升本车速度的同时不阻碍后车行驶,但是较低的换道率对于交通流量的提升作用有限。
|
| 图 4 换道成功率与车辆密度的关系 Fig. 4 Relationship between lane-changing rate and vehicle density |
| |
3.3 时空图分析
截取3个不同换道规则模型下的时空斑图,如图 5所示。

|
| 图 5 三种模型的时空斑 Fig. 5 Temporal-spatial pattern of 3 models |
| |
由图 5可以看出,STCA模型下的时空斑图像存在严重的相分离现象,阻塞频率出现较高,且持续时间较长,表示现实道路资源利用不足。本文的强制换道模型中阻塞频率降低,相分离现象减弱,持续时间缩短。协作换道模型中阻塞相现象更为减弱,虽然偶尔出现,但持续时间很短,影响更小,道路资源能够得到合理利用。
4 结论利用元胞自动机理论对自由换道、强制换道和协作换道3种换道方式进行了建模分析,并确定了不同换道方式的状态更新规则。在传统STCA换道模型的基础上,考虑更多的换道影响因素,建立了更符合交通流运行状态的换道模型;主要考虑道路交通流密度,建立了自由换道模型; 考虑相对间距、相对速度和最迟换道距离, 建立了强制换道模型;在满足车辆信息交互的基础上,考虑目标车道跟随车的驾驶员行为特性, 建立了协作换道模型。通过对3种模型的仿真对比可知,协作换道模型得到的平均速度高于其他换道模型,说明车辆之间的信息交互提高了换道成功率,使道路资源得到充分利用。协作换道在提高交通流速度和减缓交通堵塞方面比普通换道模型有更好的效果,目前道路车流密度愈来愈大,相对于传统换道和强制换道,协作换道更具有指导性和实用性。
| [1] | 贾斌, 高自友, 李克平, 等. 基于元胞自动机的交通系统建模与模拟[M]. 北京: 科学出版社, 2007 . JIA Bin, GAO Zi-you, LI Ke-ping, et al. Models and Simulations of Traffic System Based on the Theory of Cellular Automaton[M]. Beijing: Science Press, 2007 . |
| [2] | CREMER M, LUDWIG J. A Fast Simulation Model for Traffic Flow on the Basic of Boolean Operation[J]. Mathematics and Computers in Simulation , 1986, 28 (4) : 297-303 |
| [3] | WOLFRAM S. Statistical Mechanics of Cellular Automata[J]. Reviews of Modern Physics , 1983, 55 (3) : 601-644 |
| [4] | NAGGEL K, SCHRECKENBERG M. A Cellular Automaton Model for Freeway Traffic[J]. Journal of Physics , 1992, 2 (12) : 2221-2229 |
| [5] | NAGATANI T. Self-organization and Phase Transition in Traffic-flow Model of a Two-lane Roadway[J]. Journal of Physics A:Mathematical and General , 1993, 26 (17) : L781-L787 |
| [6] | DAOUDIA A K, MOUSSA N. Numerical Simulations of a Three-lane Traffic Model Using Cellular Automata[J]. Chinese Journal of Physics , 2003, 41 (6) : 671-681 |
| [7] | 刘小明, 王秀英. 基于信息交互的元胞自动机换道行为模型研究[J]. 计算机应用研究 , 2010, 27 (10) : 3826-3827 LIU Xiao-ming, WANG Xiu-ying. Study of Vehicle Lane-changing Behavior Model of Cellular Automata Based on Information Interaction[J]. Application Research of Computers , 2010, 27 (10) : 3826-3827 |
| [8] | 史丹丹, 朱正旺, 刘好德. 考虑车-车通信的双车道元胞自动机交通流模型[J]. 公路交通科技 , 2009, 26 (S1) : 142-146 SHI Dan-dan, ZHU Zheng-wang, LIU Hao-de. A Cellular Automaton Model of Traffic Flow Considering Vehicle-vehicle Communication[J]. Journal of Highway and Transportation Research and Development , 2009, 26 (S1) : 142-146 |
| [9] | 杨海飞, 路肩, 祁玥. 基于宏观运动波和微观元胞自动机的双车道交通流混合建模[J]. 东南大学学报:自然科学版 , 2012, 42 (4) : 773-778 YANG Hai-fei, LU Jian, QI Yue. Hybrid Modeling of Two-lane Traffic Flow Based on Macroscopic Kinematic Wave and Microscopic Cellular Automata[J]. Journal of Southeast University:Natural Science Edition , 2012, 42 (4) : 773-778 |
| [10] | SHI Jun-qing, CHENG Lin, LONG Jian-cheng, et al. A New Cellular Automaton Model for Urban Two-way Road Networks[J]. Computational Intelligence and Science , 2014, 2014 : 685047 |
| [11] | 施俊庆, 程琳, 褚昭明, 等. 城市路网交通流元胞自动机模型研究[J]. 公路交通科技 , 2015, 32 (4) : 143-149 SHI Jun-qing, CHEN Lin, CHU Zhao-ming, et al. Cellular Automata Model of Urban Road Network Traffic Flow[J]. Journal of Highway and Transportation Research and Development , 2015, 32 (4) : 143-149 |
| [12] | 商蕾, 陆化普. 多车道下的车辆行为模型研究[J]. 华中科技大学学报:自然科学版 , 2007, 35 (6) : 115-117 SHANG Lei, LU Hua-pu. Model of Vehicle Behavior under Multilane Road Conditions[J]. Journal of Huazhong University of Science and Technology:Nature Science Edition , 2007, 35 (6) : 115-117 |
| [13] | HIDAS P. Modeling Vehicle Interaction in Microscopic Simulation of Merging and Weaving[J]. Transportation Research Part C Emerging Technologies , 2005, 13 (1) : 37-62 |
| [14] | 刘有军, 曹珊. 基于元胞自动机的强制换道模型研究[J]. 交通信息与安全 , 2009, 27 (3) : 78-80 LIU You-jun, CAO Shan. Compulsory Lane-changing Traffic Model Based on Cellular Automaton[J]. Traffic Information and Security , 2009, 27 (3) : 78-80 |
| [15] | YANG Xiao-bao. A Lane-changing Model Considering the Maneuver Process and Its Applications[J]. Acta Physica Sinica , 2009, 58 (2) : 836-842 |
 2016, Vol. 33
2016, Vol. 33
